K 2pi лямбда что это

Обновлено: 05.02.2025

©А. Пахомов 2007 (aka IS_ 18 , Ижевск)

На написание этого материала натолкнуло обилие вопросов на нашем форуме, связанных с непониманием (или недопониманием) принципа работы датчика кислорода, или лямбда-зонда.

Прежде всего, нужно идти от общего к частному и понимать работу системы в целом. Только тогда сложится правильное понимание работы этого весьма важного элемента ЭСУД и станут понятны методы диагностики.

Чтоб не углубляться в дебри и не перегружать читателя информацией, я поведу речь о циркониевом лямбда-зонде, используемом на автомобилях ВАЗ. Желающие разобраться более глубоко могут самостоятельно найти и прочитать материалы про титановые датчики, про широкополосные датчики кислорода (ШДК) и придумать методы их проверки. Мы же поговорим о самом распространенном датчике, знакомом большинству диагностов.

Итак, датчик кислорода. Когда-то очень давно он представлял собой только лишь чувствительный элемент, без какого-либо подогревателя. Нагрев датчика осуществлялся выхлопными газами и занимал весьма продолжительное время. Жесткие нормы токсичности требовали быстрого вступления датчика в полноценную работу, вследствие чего лямбда-зонд обзавелся встроенным подогревателем. Поэтому датчик кислорода ВАЗ имеет 4 вывода: два из них – подогреватель, один – масса, еще один – сигнал.

Из всех этих выводов нас интересует только сигнальный. Форму напряжения на нем можно увидеть двумя способами:

а) сканером
б) мотортестером, подключив щупы и запустив самописец.

Второй вариант, вообще говоря, предпочтительнее. Почему? Потому, что мотортестер дает возможность оценить не только текущие и пиковые значения, но и форму сигнала, и скорость его изменения. Скорость изменения – это как раз характеристика исправности датчика.

Итак, главное: датчик кислорода реагирует на кислород. Не на состав смеси. Не на угол опережения зажигания. Не на что-либо еще. Только на кислород. Это нужно осознать обязательно. Как именно это происходит, в подробностях описано здесь.

На сигнальный вывод датчика с ЭБУ подается опорное напряжение 0 . 45 В. Чтоб быть полностью уверенным, можно отключить разъем датчика и проверить это напряжение мультиметром или сканером. Все в порядке? Тогда подключаем датчик обратно.

Для более глубокого понимания добавлю, что при наличии небольшого опыта легко установить степень изношенности датчика. Это делается по крутизне фронтов перехода с богатой смеси на бедную и обратно. Хороший, исправный датчик реагирует быстро, переход почти что вертикальный (смотреть, само собой, мотортестером). Отравленный либо просто изношенный датчик реагирует медленно, фронты переходов пологие. Такой датчик требует замены.

Понимая, что датчик реагирует на кислород, можно легко уяснить еще один распространенный момент. При пропусках воспламенения, когда из цилиндра в выпускной тракт выбрасывается смесь атмосферного воздуха и бензина, лямбда-зонд отреагирует на большое количество кислорода, содержащееся в этой смеси. Поэтому при пропусках воспламенения очень возможно возникновение ошибки, указывающей на бедную топливо-воздушную смесь.

1 . Нужно совершенно четко отличать неисправность ЭСУД от неисправности лямбда-зонда.

2 . Проверить зонд можно, контролируя напряжение на его сигнальном выводе сканером или подключив к сигнальному выводу мотортестер.

3 . Искусственно смоделировав обедненную или, наоборот, обогащенную смесь и отследив реакцию зонда, можно сделать достоверный вывод о его исправности.

5 . Наличие ошибки, указывающей на дефект лямбда-зонда, отнюдь не является поводом для его замены.

Я решил написать эту серию статей, ибо считаю, что никто не должен сталкиваться с той стеной непонимания, с которой столкнулся когда-то я.

Ведь большинство статей написаны таки образом что, для того чтобы понять что-то в Функциональном Программировании (далее ФП), тебе надо уже знать многое в ФП. Эту статью я старался написать максимально просто — настолько понятно, чтобы её суть мог уловить мой племянник, школьник, который сейчас делает свои первые шаги в Python.

Небольшое введение

• Чистая Функция
• Функции высшего порядка

Чистая Функция — Функция которая является детерминированной и не обладает никакими побочными эффектами.

То есть чтобы функция являлась чистой она должна быть детерминированной — то есть каждый раз при одинаковом наборе аргументов выдавать одинаковый результат.

Пример детерминированной функции

И пример не детерминированной:

Каждый раз при смене дня недели (который не является аргументом функции) функция выдает разные результаты.

Самый очевидный пример не детерминированной функции это random:

Второе важное качество чистой функции это отсутствие побочных эффектов.

Функция sort_by_sort имеет побочные эффекты потому что изменяет исходный список элементов и выводит что то в консоль.

В отличии от предыдущего примера функция sort_by_sorted не меняет исходного массива и возвращает результат не выводя его в консоль самостоятельно.

Чистые функции хороши тем что:

• Они проще читаются
• Они проще поддерживаются
• Они проще тестируются
• Они не зависят от того в каком порядке их вызывать

Функции высшего порядка — в программировании функция, принимающая в качестве аргументов другие функции или возвращающая другую функцию в качестве результата.

С основами чуть чуть разобрались и теперь перейдем к следующему шагу.

Итак, начнем

Для начала надо понять следующее — что такое Функциональное Программирование вообще. Лично я знаю две самые часто упоминаемые парадигмы в повседневном программировании — это ООП и ФП.

Если упрощать совсем и объяснять на пальцах, то описать эти две парадигмы можно следующим образом:

• ООП — это Объектно Ориентированное Программирование — подход к программированию, при использовании которого объекты можно передавать в качестве параметров и использовать их в качестве значений.
• По такой логике можно установить, что ФП — подход к программированию, при использовании которого функции можно передавать другим функциям в качестве параметров и использовать функции в качестве значений, возвращаемых другими функциями… Ответ скрыт в самом названии.

Это относится и к ФП — взял какие-то данные, взял какую-то функцию, поигрался с ними и выдал что-то на выходе.

Не стану расписывать всё, иначе это будет оооочень долго. Цель данной статьи — помочь разобраться, а не объяснить, как и что работает, поэтому тут мы рассмотрим основные функции из ФП.

В большинстве своем ФП (как я его воспринимаю) — это просто упрощенное написание кода. Любой код, написанный в функциональном стиле, может быть довольно легко переписан в обычном стиле без потери качества, но более примитивно. Цель ФП заключается в том, чтобы писать код более простой, понятный и который легче поддерживать, а также который занимает меньше памяти, ну и куда же без этого — разумеется, главная вечная мораль программирования — DRY (Don’t Repeat Yourself — Не повторяйся).

Сейчас мы с вами разберем одну из основных функций, которая применяется в ФП — Lambda функцию.

В следующих статьях мы разберем такие функции как Map, Zip, Filter и Reduce.

Lambda функция

Lambda — это инструмент в python и других языках программирования для вызова анонимных функций. Многим это скорее всего ничего не скажет и никак не прояснит того, как она работает, поэтому я расскажу вам просто механизм работы lambda выражений.

Все очень просто.

Рассмотрим пример. Например, нам надо написать функцию которая бы считала площадь круга при известном радиусе.

Формула площади круга это

где
S — это площадь круга
pi — математическая константа равная 3.14 которую мы получим из стандартной библиотеки Math
r — радиус круга — единственная переменная которую мы будем передавать нашей функции

Теперь оформим это все в python:

Вроде бы неплохо, но это всё может выглядеть куда круче, если записывать это через lambda:

Чтобы было понятнее, анонимный вызов функции подразумевает то, что вы используете её, нигде не объявляя, как в примере выше.

Лямбда функция работает по следующему принципу

Рассмотрим пример с двумя входными аргументами. Например, нам надо посчитать объем конуса по следующей формуле:

Запишем это все в python:

А теперь как это будет выглядеть в lambda форме:

Количество переменных здесь никак не ограничено. Для примера посчитаем объем усеченного конуса, где у нас учитываются 3 разные переменные.

Объем усеченного конуса считается по формуле:

И вот, как это будет выглядеть в python классически:

А теперь покажем, как это будет выглядеть с lambda:

После того, как мы разобрались, как работает lambda функция, давайте разберем ещё кое-что интересное, что можно делать с помощью lambda функции, что может оказаться для вас весьма неожиданным — Сортировку.

Сортировать одномерные списки в python с помощью lambda довольно глупо — это будет выглядеть, как бряцание мускулами там, где оно совсем не нужно.

Ну серьезно допустим, у нас есть обычный список (не важно состоящий из строк или чисел) и нам надо его отсортировать — тут же проще всего использовать встроенную функцию sorted(). И в правду, давайте посмотрим на это.

В таких ситуациях, действительно, хватает обычного sorted() (ну или sort(), если вам нужно изменить текущий список на месте без создания нового, изменив исходный).

Но что, если нужно отсортировать список словарей по разным ключам? Тут может быть запись как в классическом стиле, так и в функциональном. Допустим, у нас есть список книг вселенной Песни Льда и Пламени с датами их публикаций и количеством страниц в них.

Как всегда, начнем с классической записи.

А теперь перепишем это все через lambda функцию:

Таким образом, lambda функция хорошо подходит для сортировки многомерных списков по разным параметрам.

Если вы повторите весь этот код самостоятельно, написав его сами, то я уверен, что с этого момента вы сможете сказать, что отныне вы понимаете, как работают lambda выражения, и сможете применять их в работе.

Но где же тут та самая экономия места, времени и памяти? Экономится максимум пара строк.

Основным стимулом для дыхания организма является повышение уровня углекислого газа (CO2). Мозг контролирует вентиляцию. С помощью мышечных сокращений воздух (как правило, состоит из 79% азота и 21% кислорода) поступает через дыхательные пути в легкие и заполняет альвеолы, где происходит газообмен. Он совершается с помощью процесса, называемого "диффузией" - движением молекул из области высокой концентрации в область низкой концентрации. Эта диффузия происходит через альвеолярную капиллярную мембрану, где CO2 в крови обменивается на кислород (O2) из воздуха.Кислород связывается с молекулами гемоглобина в эритроцитах. Насыщенная кислородом кровь поступает из легких в сердце, откуда по артериям распространяется по всему телу. Насыщенность гемоглобина артериальной крови кислородом называется сатурацией (SaO2). Значения SaO2 > 94% считаются нормальными показателями. При более низких значениях применяется кислородотерапия. Современный кислородный концентратор - это небольшой простой в управлении прибор.

Как работает пульсоксиметрия

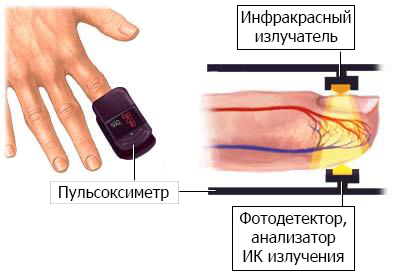
Пульсоксиметрия проводится при помощи пульсоксиметра. Пульсоксиметр является неинвазивным средством измерения как частоты пульса, так и насыщения артериального гемоглобина кислородом на периферическом капиллярном уровне.Он состоит из портативного монитора и фотоэлектрического зонда который закрепляется на перст, пальце руки или ноги или на мочке уха пациента.Зонд измеряет количество красного цвета в капилляре во время систолы и диастолы. Монитор высчитывает время между пиками и показывает величину пульса в ударах в минуту.Прибор также вычисляет значение, основанное на коэффициенте поглощения света на систоле и диастоле и показывает периферийный процент сатурации кислорода (SpO2).

Если пульсоксиметр показывает сатурацию ниже 92%, то это причина для беспокойства. Ее падение ниже 90% наводит на мысль о гипоксемии. Это значит, что концентрация кислорода в кровеносном русле более низкая, чем в клетках. Это затрудняет диффузию кислорода из клеток и назад в кровеносное русло, ведя к гипоксии ткани и в дальнейшем к смерти. Идеальной является сатурация в 94-99%, но следует иметь в виду факторы, которые могут повлиять на показания пульсоксиметра. Среди условий, которые могут сделать показания прибора ненадежными, можно отметить плохую периферическую перфузию, в том числе вызванную шоком, вазоконстрикцией (сужением кровеносных сосудов), гипотензией (пониженным артериальным давлением). Нельзя прикреплять чувствительный зонд к поврежденной конечности. Нельзя использовать прибор на той же руке, на которой измеряется артериальное давление. Следует иметь в виду, что показания пульсоксиметра будут идти вниз в то время, когда манжета тонометра надувается. Она будет закрывать артериальный кровоток, влияющий на показания,

Изменения, происходящие в области медицины, а также связанные с ними электронные переносные устройства, можно назвать поистине революционными. Приборы, которые раньше можно было найти только в стационарах теперь доступны для домашнего медицинского применения, Хорошим примером является концентратор кислорода для дома. Соответственно, пульсоксиметры используются медсестрами в больницах, амбулаторными пациентами дома, любителями фитнеса в тренажерном зале и даже пилотами в самолетах. Пульсоксиметрия наиболее информативный метод определения содержания кислорода к крови.

Пульсоксиметрия. Степени кислородной недостаточности относительно сатурации (SpO2) - показания пульсоксиметра

Степень	SpO2,% (Показания пульсоксиметрии)
Норма	более или равно 95%
1 степень	90-94%
2 степень	75-89%
3 степень	менее 75%
Гипоксемическая кома	менее 60%

Показатель PI на пульсоксиметре. Индекс перфузии (PI) – это интенсивность объемного периферического кровотока, иными словами PI — сила пульса в месте измерения.

Величина PI измеряется в диапазоне 0,02–20,0%.

Рекомендации, необходимый поток кислорода, режим и длительность кислородной терапии, назначает лечащий врач! Кислородотерапия в домашних условиях проводится с помощью кислородных концентраторов под контролем показаний пульсоксиметра.

Демонстрационное видео. Пульсоксиметрия пульсоксиметром Армед YX301

Лямбда-исчисление (англ. lambda calculus) — формальная система, придуманная в 1930-х годах Алонзо Чёрчем. Лямбда-функция является, по сути, анонимной функцией. Эта концепция показала себя удобной и сейчас активно используется во многих языках программирования.

Содержание

[math] \Lambda \to V\\ \Lambda \to \Lambda \ \Lambda\\ \Lambda \to \lambda V . \Lambda [/math]

Пробел во втором правиле является терминалом грамматики. Иногда его обозначают как @, чтобы он не сливался с другими символами в выражении.

В первом случае функция является просто переменной. Во втором происходит аппликация (применение) одной функции к другой. Это аналогично вычислению функции-левого операнда на аргументе-правом операнде. В третьем — абстракция по переменной. В данном случае происходит создание функции одного аргумента с заданными именем аргумента и телом функции.

Рассмотрим, например, [math]\lambda[/math] -терм [math]\operatorname = \lambda x\ .\ x[/math] . Эта функция принимает аргумент и возвращает его неизменённым. Например, [math]\operatorname\ 2 \equiv 2[/math] . Аналогично, [math]\operatorname\ y \equiv y[/math] .

[math] x\\ (x\ z)\\ (\lambda x.(x\ z))\\ (\lambda z.(\lambda w.((\lambda y.((\lambda x.(x\ z))\ y))\ w)))\\ [/math]

Иногда [math]\lambda[/math] -термы пишут по другому. Для краткости подряд идущие лямбды заменяют на одну. Например:

[math]\lambda x\ .\ \lambda y\ .P\ \to\ \lambda xy.P[/math]

• Аппликация: [math]x\ y\ z\ w \equiv ((x\ y)\ z)\ w[/math]
• Абстракция забирает себе всё, до чего дотянется: [math]\lambda x\ .\ \lambda y\ .\ \lambda z\ .\ z\ y\ x \equiv \lambda x\ .\ (\lambda y\ .\ (\lambda z\ .\ ((z\ y)\ x)))[/math]
• Скобки играют привычную роль группировки действий

Связанными переменными называются все переменные, по которым выше в дереве разбора были абстракции. Все остальные переменные называются свободными.

Например, в [math]\lambda x\ .\ y\ x[/math] , [math]x[/math] и связана, а [math]y[/math] — свободна. А в [math]\lambda y\ .\ x\ (\lambda x\ .\ x)[/math] в своём первом вхождении переменная [math]x[/math] свободна, а во втором — связана.

Связанные переменные — это аргументы функции. То есть для функции они являются локальными.

Рассмотрим функции [math]\lambda y\ .\ y[/math] и [math]\lambda x\ .\ y[/math] . В первой из них при взгляде на [math]y[/math] понятно, что она имеет отношение к переменной, по которой производилась абстракция. Если по одной и той же переменной абстракция производилась более одного раза, то переменная связана с самым поздним (самым нижним в дереве разбора) абстрагированием. Например, в [math]\lambda x\ .\ \lambda x\ .\ \lambda y\ .\ \lambda x\ .\ x[/math] , переменная [math]x[/math] связана с самой правой абстракцией по [math]x[/math] .

и замкнуто относительно следующих правил:

Функции [math]\lambda x\ .\ \lambda y\ .\ x\ y\ z[/math] и [math]\lambda a\ .\ \lambda x\ .\ a\ x\ z[/math] являются [math]\alpha[/math] -эквивалентными, а [math]\lambda x\ .\ \lambda y\ .\ y\ z[/math] и [math]\lambda y\ .\ \lambda x\ .\ y\ z[/math] — нет.

и замкнуто относительно следующих правил

В [math]\beta[/math] -редукции вполне возможна функция вида [math]\lambda x. \lambda x.x[/math] . Во время подстановки вместо [math]x[/math] внутренняя переменная не заменяется - действует принцип локальной переменной. Но принято считать, что таких ситуаций не возникает и все переменные называются разными именами.

Существует также альтернативное эквивалентное определение [math]\lambda[/math] -исчисления. В оригинальном определении для обозначения переменных использовались имена, и была проблема с тем, что не были запрещены одинаковые имена в разных абстракциях.

От этой проблемы можно избавиться следующим образом. Вместо имени переменной будет храниться натуральное число — количество абстракций в дереве разбора, на которое нужно подняться, чтобы найти ту лямбду, с которой данная переменная связана. В данной нотации получаются несколько более простые определения свободных переменных и [math]\beta[/math] -редукции.

Грамматику нотации можно задать как:

[math]e\ ::= n\ |\ \lambda .e\ |\ e\ e[/math]

Примеры выражений в этой нотации:

Standart	de Bruijn
$\lambda x.x$	$\lambda .0$
$\lambda z.z$	$\lambda .0$
$\lambda x. \lambda y.x$	$\lambda . \lambda .1$
$\lambda x. \lambda y. \lambda s. \lambda z.x\ s\ (y\ s\ z)$	$\lambda . \lambda . \lambda . \lambda .3\ 1(2\ 1\ 0)$
$(\lambda x.x\ x)(\lambda x.x\ x)$	$(\lambda .0\ 0)(\lambda .0\ 0)$
$(\lambda x. \lambda x.x)(\lambda y.y)$	$(\lambda .\lambda .0)(\lambda .0)$

Переменная называется свободной, если ей соответствует число, которое больше количества абстракций на пути до неё в дереве разбора.

Введём на основе лямбда-исчисления аналог натуральных чисел, основанный на идее, что натуральное число — это или ноль, или увеличенное на единицу натуральное число.

[math]\bar 0 = \lambda s\ .\ \lambda z\ .\ z[/math] [math]\bar 1 = \lambda s\ .\ \lambda z\ .\ s\ z[/math] [math]\bar 2 = \lambda s\ .\ \lambda z\ .\ s\ (s\ z)[/math] [math]\bar 3 = \lambda s\ .\ \lambda z\ .\ s\ (s\ (s\ z))[/math]

Каждое число будет функцией двух аргументов: какой-то функции и начального значения. Число [math]n[/math] будет [math]n[/math] раз применять функцию к начальному значению и возвращать результат. Если такому "числу" дать на вход функцию [math](+1)[/math] и [math]0[/math] в качестве начального значения, то на выходе как раз будет ожидаемое от функции число: [math]\bar 3\ (+1)\ 0 \equiv 3[/math] .

Функция, прибавляющая [math]1[/math] к числу, должна принимать первым аргументом число. Но число — функция двух аргументов. Значит, эта функция должна принимать три аргумента: "число" [math]n[/math] , которое хочется увеличить, функция, которую надо будет [math]n+1[/math] раз применить, и начальное значение.

[math]\operatorname = \lambda n\ .\ \lambda s\ .\ \lambda z\ .\ s\ (n\ s\ z)[/math]

Здесь [math]n\ s\ z[/math] — [math]n[/math] раз применённая к [math]z[/math] функция [math]s[/math] . Но нужно применить [math]n+1[/math] раз. Отсюда [math]s\ (n\ s\ z)[/math] .

Сложение двух чисел похоже на прибавление единицы. Но только надо прибавить не единицу, а второе число.

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \lambda s\ .\ \lambda z\ .\ n\ s\ (m\ s\ z)[/math]

[math]n[/math] раз применить [math]s[/math] к применённому [math]m[/math] раз [math]s[/math] к [math]z[/math]

[math](\operatorname\ \bar 3\ \bar 3)\ (+1)\ 0 \equiv 6[/math]

[math](\operatorname\ ((\operatorname\ 2\ 5)(+1)\ 0)\ 4)(+1)0 \equiv 11[/math]

Умножение похоже на сложение, но прибавлять надо не единицу, а второе число. Или, в терминах нумералов Чёрча, в качестве применяемой несколько раз функции должна быть не [math]s[/math] , а функция, применяющая [math]n[/math] раз [math]s[/math] .

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \lambda s\ .\ \lambda z\ .\ n\ (m\ s)\ z[/math]

Здесь [math]m\ s[/math] — функция, которая [math]m[/math] раз применит [math]s[/math] к тому, что дадут ей на вход. С помощью [math]\eta[/math] -редукции можно немного сократить эту формулу

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \lambda s\ .\ n\ (m\ s)[/math]

[math](\operatorname \bar 3\ \bar 3)\ (+1)\ 0 \equiv 9[/math]

It's a kind of magic

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \lambda s\ .\ \lambda z\ .\ m\ n\ s\ z[/math]

[math](\operatorname\ \bar 3\ (\operatorname\ \bar 3))\ (+1)\ 0 \equiv 81[/math]

[math]\operatorname = \lambda a\ .\ \lambda b\ .\ a[/math]

[math]\operatorname = \lambda a\ .\ \lambda b\ .\ b[/math]

Функции двух аргументов, возвращающие первый и второй, соответственное, аргументы. Забавный факт: [math]\operatorname \equiv_\alpha \operatorname[/math] . Эти функции сделаны такими для того, чтобы красиво написать функцию [math]\operatorname[/math] :

[math]\operatorname = \lambda p\ .\ \lambda t\ .\ \lambda e\ .\ p\ t\ e[/math]

Если ей в качестве первого аргумента дадут [math]\operatorname[/math] , то вернётся [math]t[/math] , иначе — [math]e[/math] .

Стандартные функции булевой логики:

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \operatorname\ n\ m\ \operatorname[/math]

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \operatorname\ n\ \operatorname \ m[/math]

[math]\operatorname = \lambda b\ .\ \operatorname\ b\ \operatorname \ \operatorname[/math]

Ещё одной важной функцией является функция проверки, является ли число нулём:

[math]\operatorname = \lambda n\ .\ n\ (\lambda c\ .\ \operatorname)\ \operatorname[/math]

Функция выглядит несколько странно. [math]\lambda c \to \operatorname[/math] - функция, которая независимо от того, что ей дали на вход, возвращает [math]\operatorname[/math] . Тогда, если в качестве [math]n[/math] будет дан ноль, то функция, по определению нуля, не выполнится ни разу, и будет возвращено значение по умолчанию [math]\operatorname[/math] . Иначе же функция будет запущено, и вернётся [math]\operatorname[/math] .

[math]\operatorname = \lambda a\ .\ \lambda b\ .\ \lambda t\ .\ t\ a\ b[/math]

[math]\operatorname = \lambda p\ .\ p\ \operatorname[/math]

[math]\operatorname = \lambda p\ .\ p\ \operatorname[/math]

Функция [math]\operatorname[/math] принимает два значения и запаковывает их в пару так, чтобы к ним можно было обращаться по [math]\operatorname[/math] и [math]\operatorname[/math] . В [math]\operatorname[/math] и [math]\operatorname[/math] вместо [math]t[/math] в [math]\operatorname[/math] будет подставлено [math]\operatorname[/math] или [math]\operatorname[/math] , возвращающие, соответственно, первый и второй аргументы, то есть [math]a[/math] или [math]b[/math] , соответственно.

В отличие от всех предыдущих функций, вычитание для натуральных чисел определено только в случае, если уменьшаемое больше вычитаемого. Положим в противном случае результат равным нулю. Пусть уже есть функция, которая вычитает из числа единицу. Тогда на её основе легко сделать, собственно, вычитание.

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ m\ \operatorname n[/math]

Это то же самое, что [math]m[/math] раз вычесть единицу из [math]n[/math] .

Осталось, собственно, функция для вычитания единицы. Однако, это не так просто, как может показаться на первый взгляд. Проблема в том, что, имея функцию, которую нужно применить для того, чтобы продвинуться вперёд, продвинуться назад будет проблематично. Если попробовать воспользоваться идеей о том, чтобы, начав от нуля, идти вперёд, и пройти на один шаг меньше, то будет не очень понятно, как же остановиться ровно за один шаг до конца. Для реализации вычитания единицы сделаем следующее. [math]n[/math] раз выполним следующее: имея пару [math]\langle n-1, n-2\rangle[/math] построим пару [math]\langle n, n-1\rangle[/math] . Тогда после [math]n[/math] шагов во втором элементе пары будет записано число [math]n-1[/math] , которое и хочется получить.

[math]\operatorname = \lambda n\ .\ \lambda s\ .\ \lambda z.\ \operatorname\ ( n\ ( \lambda p\ .\ \operatorname\ (s\ (\operatorname p))\ (\operatorname p) )\ (\operatorname\ z\ z))[/math]

Если вы ничего не поняли, не огорчайтесь. Вычитание придумал Клини, когда ему вырывали зуб мудрости. А сейчас наркоз уже не тот.

Так как вычитание определено таким способом, чтобы для случая, в котором уменьшаемое больше, чем вычитаемое, возвращать ноль, можно определить сравнение на больше-меньше через него. Равными же числа [math]a[/math] и [math]b[/math] считаются, если [math]a - b = 0 \wedge b - a = 0[/math] .

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ n\ m)[/math]

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \operatorname\ n\ (\operatorname m)[/math]

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ (\operatorname\ n\ m))\ (\operatorname\ (\operatorname\ m\ n))[/math]

Попробуем выразить в лямбда-исчислении какую-нибудь функцию, использующую рекурсию. Например, факториал.

[math]\operatorname = \lambda x\ .\ \operatorname\ (\operatorname\ x)\ \bar 1\ (\operatorname\ (\operatorname\ x))[/math]

Мы столкнулись с проблемой. В определении функции [math]\operatorname[/math] используется функция [math]\operatorname[/math] . При формальной замене, получим бесконечную функцию. Можно попытаться решить эту проблему следующим образом

[math]\operatorname = (\lambda f\ .\ \lambda x\ .\ \operatorname\ (\operatorname\ x)\ \bar 1\ (f\ (\operatorname\ x)))\ \operatorname[/math]

Лямбда исчисление обладаем замечательным свойством: у каждой функции есть неподвижная точка!

Рассмотрим следующую функцию.

[math]\operatorname = \lambda f\ .\ (\lambda x\ .\ f\ (x\ x))\ (\lambda x\ .\ f\ (x\ x))[/math]

Заметим, что [math]\operatorname \to_\beta^* \lambda f\ .\ f\ ((\lambda x\ .\ f\ (x\ x))\ (\lambda x\ .\ f\ (x\ x)))[/math] . Или, что то же самое, [math]\lambda f\ .\ (\lambda x\ .\ f\ (x\ x))\ (\lambda x\ .\ f\ (x\ x)) \to_\beta^*[/math] [math]\lambda f\ .\ f\ ((\lambda x\ .\ f\ (x\ x))\ (\lambda x\ .\ f\ (x\ x)))[/math]

[math]\operatorname = \lambda f\ .\ \lambda x\ .\ \operatorname\ (\operatorname\ x)\ \bar 1\ (\operatorname\ x\ (f\ (\operatorname\ x)))[/math]

Как было показано выше, [math]\operatorname f \to_\beta^* f\ (\operatorname f)[/math] , то есть, [math]\operatorname\ \operatorname \to_\beta^* \operatorname[/math] , где [math]\operatorname[/math] — искомая функция, считающая факториал.

[math]\operatorname = \operatorname\ \operatorname[/math]

Это даст функцию, которая посчитает факториал числа. Но делать она это будет мееедленно-меееедленно. Для того, чтобы посчитать [math]5![/math] потребовалось сделать 66066 [math]\beta[/math] -редукций.

Наиболее известным комбинатором неподвижной точки является [math]Y[/math] -комбинатор, введенный известным американским ученым Хаскеллом Карри как

[math]Y\ = \ \lambda f.(\lambda x.f(x\ x))\ (\lambda x.f(x\ x))[/math]

Воспользовавшись идеей о том, что можно делать рекурсивные функции, сделаем функцию, которая будет искать частное двух чисел.

[math]\operatorname = \lambda div\ .\ \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ n\ m)\ \bar 0\ (\operatorname\ (div\ (\operatorname\ n\ m)\ m))[/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

И остатка от деления

[math]\operatorname = \lambda mod\ .\ \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ n\ m)\ n\ (mod\ (\operatorname\ n\ m)\ m)[/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

[math]\operatorname[/math] — принимает число, которое требуется проверить на простоту и то, на что его надо опытаться поделить, перебирая это от [math]2[/math] до [math]p-1[/math] . Если на что-нибудь разделилось, то число — составное, иначе — простое.

[math]\operatorname =[/math] [math]\lambda f\ .\ \lambda p\ .\ \lambda i\ .\ \operatorname\ (\operatorname\ p\ i)\ \operatorname\ (\operatorname\ (\operatorname\ (\operatorname\ p\ i))\ \operatorname\ (f\ p\ (\operatorname\ i)))[/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

[math]\operatorname = \lambda p\ .\ \operatorname\ p\ \bar 2[/math]

Следующее простое число. [math]\operatorname[/math] — следующее, больше либо равное заданного, [math]\operatorname[/math] — следующее, большее заданного.

[math]\operatorname = \lambda f\ .\ \lambda p\ .\ \operatorname\ (\operatorname\ p)\ p\ (f\ (\operatorname\ p)) [/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

[math]\operatorname = \lambda p\ .\ \operatorname\ (\operatorname\ p)[/math]

[math]\operatorname[/math] пропрыгает [math]i[/math] простых чисел вперёд. [math]\operatorname[/math] принимает число [math]i[/math] и пропрыгивает столько простых чисел вперёд, начиная с двойки.

[math]\operatorname = \lambda f\ .\ \lambda p\ .\ \lambda i\ .\ \operatorname\ (\operatorname\ i)\ p\ (f\ (\operatorname\ p)\ (\operatorname\ i))[/math]

[math]\operatorname = \lambda i\ .\ \operatorname\ \bar 2\ i[/math]

. и всего через 314007 [math]\beta[/math] -редукций вы узнаете, что третье простое число — семь!

Для работы со списками чисел нам понадобятся следующие функции:

• [math]\operatorname[/math] — возвращает пустой список
• [math]\operatorname[/math] — принимает первый элемент и оставшийся список, склеивает их
• [math]\operatorname[/math] — вернуть голову списка
• [math]\operatorname[/math] — вернуть хвост списка

[math]\operatorname = \operatorname\ \operatorname\ \bar 1[/math]

[math]\operatorname = \lambda h\ .\ \lambda t\ .\ \operatorname\ (\operatorname\ (\operatorname\ t))\ (\operatorname\ (\operatorname\ t)\ (\operatorname\ (\operatorname\ (\operatorname\ t))\ h))[/math]

[math]\operatorname = \lambda list\ .\ \operatorname\ (\operatorname\ list)\ (\operatorname\ (\operatorname\ (\operatorname\ list)))[/math]

[math]\operatorname = \lambda list\ .\ \operatorname\ (\operatorname\ (\operatorname\ list)) (\operatorname\ (\operatorname\ list)\ (\operatorname\ (\operatorname\ (\operatorname\ list))))[/math]

[math]\operatorname =[/math] [math] \lambda f\ .\ \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ (\operatorname\ n\ m))\ (f\ (\operatorname\ n\ m)\ m)\ n[/math]

[math]\operatorname =[/math] [math] \lambda f\ .\ \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ (\operatorname\ n\ m))\ (\operatorname\ (f\ (\operatorname\ n\ m)\ m))\ \bar 0[/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

Читайте также:

  
• Установка ксенона в гетц
  
• Неисправности видеорегистратора системы видеонаблюдения
  
• Как подключить радио в машине к магнитоле
  
• Фиат брава слабые места
  
• Киа опирус замена свечей