Свет с длиной волны падает нормально на дифракционную решетку с периодом d 3 лямбда
При исследовании спектра ртути с помощью дифракционной решётки и гониометра (прибора для точного измерения углов дифракции света) было обнаружено, что в спектре 3-го порядка вблизи двойной жёлтой линии ртути со средней длиной волны \(\lambda_1= 578\) нм видна сине-фиолетовая линия 4-го порядка. Оцените её длину волны \(\lambda_2\) (в нм).
Формула для дифракционной решетки: \[dsin\alpha=m_3\lambda_1=m_4\lambda_2\] \(d\) – период дифракционной решетки, \(m\) – порядок дифракционного максимума, \(\lambda\) – длина волны, \(\alpha\) – угол наблюдения данного максимума. Максимальный синус равен 1, следовательно: \[\lambda_2=\frac
Определите постоянную дифракционной решетки (в нм), если при нормальном падении света на решетку зеленая линия спектра лампы (длина волны 550 нм) наблюдается в пятом порядке под углом \(30^\) .
Формула для дифракционной решетки: \[d\sin\alpha=m\lambda\] \(d\) – постоянная дифракционной решетки, \(m\) – порядок дифракционного максимума, \(\lambda\) – длина волны, \(\varphi\) – угол наблюдения данного максимума. Максимальный синус равен 1, следовательно: \[d=\frac
На дифракционную решетку, период которой равен \(d=2\text< мкм>\) нормально падает пучок света, состоящий из фотонов с импульсом \(p=1,32\cdot10^\text< кг>\) \(\cdot \text\) . Под каким углом \(\varphi\) к направлению падения пучка наблюдается дифракционный максимум третьего порядка? Ответ дайте в градусах, округлив до целых.
Углы, определяющие направления на дифракционные максимумы, при нормальном падении пучка на решетку удовлетворяют условию \(d\sin\varphi=m\lambda\) где \(\lambda\) — длина волны света, \(m=3\) .
Импульс фотона связан с его длиной волны \(\lambda\) соотношением \(p=\dfrac<\lambda>\) где \(h\) — постоянная Планка. Из записанных соотношений находим:
Монохроматический свет с частотой 1,5 \(\cdot \) 10 \(^\) Гц распространяется в пластинке,прозрачной для этого света и имеющей показатель преломления 1,6. Чему равна длина волны (в нм) этого света в пластинке?
Черноуцан
Показатель преломления данной среды относительно вакуума называется абсолютным показателем преломления данной среды \(n\) , его можно определить как отношение скорости света в вакууме \(c\) , к скорости света в данной среде \(v\) \[n = \frac\] Откуда: \[v = \frac\;\;\;\;(1)\] По формуле скорость света в среде равна \[v = \lambda \nu,\;\;\;\;(2)\] где \(\lambda\) – длина волны, \(\nu\) – частота света.
Приравняв (1) и (2), получим \[\dfrac=\lambda \nu \Rightarrow \lambda = \dfrac\] Подставим числа из условий: \[\lambda = \dfrac>\text< Гц>>=125\text< нм>\]
На дифракционную решетку перпендикулярно ее плоскости падает свет с длиной волны 500 нм. Сколько штрихов на 1 мм должна иметь решетка, чтобы пятый главный максимум в дифракционной картине находился под углом 90 \(^\circ\) по отношению к падающему свету?
Черонуцан
По формуле дифракционной решетки: \[d\sin \varphi_k = k\lambda,\] где \(k\) – порядок максимума, \(d\) – постоянная решетки, \(\lambda\) – длина волны решётки, \(\varphi_k\) – направление на \(k-\) й максимум.
По условию \(k=5\) , \(\varphi_k=90^\circ\) , откуда: \[d=k\lambda=5\lambda= 2500 \text< нм>\] Тогда количество штрихов на \(l=1\) мм: \[N=\dfrac=\dfrac>>=400\]
Волна красного света проходит через тонкую прозрачную пленку с показателем преломления 1,8. Толщина пленки 3,8 \(\cdot\) 10 \(^\) м. Определите, сколько раз длина волны света в пленке укладывается на ее толщине, если длина волны в вакууме 720 нм. Волна падает на пленку перпендикулярно ее плоскости.
Черноуцан
По закону преломления: \[\dfrac=n,\] где \(v\) – скорость света в среде, \(n\) – показатель преломления среды.
Частота волны при переходе из одной среды в другую не изменяется, следовательно \[c=\nu \lambda_1 \quad v = \nu \lambda_2,\] где \(\lambda_1\) – длина волны в вакууме, \(\lambda_2\) – длина волны в среде.
Тогда \[\dfrac=n \Rightarrow \lambda_2 = \dfrac<\lambda_1>\] На толщине \(d\) будет укладываться \[N=\dfrac<\lambda_1>=95\]
Для исследования рентгеновских лучей с длинами волн меньше 10 нм изготовить обычную дифракционную решётку с подходящим периодом не представляется возможным, однако есть способ обойти эту трудность. Возьмём обычную решётку с периодом \(d = 30\) мкм и осветим её параллельным пучком рентгеновского излучения с длиной волны \(\lambda = 4,5\) нм с углом падения на решётку \(\alpha = 89,5^\circ\) (скользящее падение лучей). Под каким углом \(\gamma\) к первоначальному пучку будет фиксироваться дифракционный максимум первого порядка? Считайте этот угол малым: \(\gamma
При скользящем падении лучей на дифракционную решётку с периодом \(d\) разность хода соседних лучей возникает как до их падения ( \(-d\cdot \sin \alpha\) ) так и после их выхода из решётки ( \(d\cdot \sin \varphi\) где \(\varphi\) – угол дифракции, то есть угол между перпендикуляром к плоскости решётки и лучом). Таким образом, условие первого главного максимума для дифракции на решётке в данном случае имеет вид: \(d(\sin \varphi - \sin \alpha)=\lambda \) или, согласно тригонометрической формуле, \[d\cdot 2 \sin\dfrac\cos \dfrac=\lambda\] По условию угол отклонения луча решёткой \(\gamma = \varphi-\alpha << 1\) , поэтому \(\varphi \approx \alpha\) и \(\cos \dfrac\cos \alpha\) . Значит, \[2\sin \dfrac\approx 2\sin\dfrac<\gamma>\approx \gamma\] и условие главного дифракционного максимума первого порядка приобретает вид: \(d\cos \alpha \cdot \gamma \approx \lambda,\) то есть эффективный период решётки уменьшается до \(d\cos \alpha\) и при угле \(\alpha\) , близком к \(90^\circ\) , может быть намного меньше \(d\) . Теперь можно найти угол \(\gamma\) : \[\gamma \approx \dfrac<\lambda>\approx \dfrac\text< м>>\text< м>\cdot 0,00873>\approx 1,718\cdot 10^\approx 0,984^\circ \approx 1^\circ\]
Ускоренная подготовка к ЕГЭ с репетиторами Учи.Дома. Записывайтесь на бесплатное занятие!

-->

Задание 29 № 4168
Свет с неизвестной длиной волны падает нормально на дифракционную решётку с периодом и одному из главных дифракционных максимумов соответствует угол дифракции 30°. При этом наибольший порядок наблюдаемого спектра равен 5. Найдите длину волны света, падающего на решетку, и выразите его в ангстремах.
Справка: 1 ангстрем = 10 −10 м.
Условие наблюдения главных максимумов для дифракционной решетки имеет вид В данной задаче неизвестному порядку m главного максимума соответствует угол дифракции так что где длина волны неизвестна, а m — целое число.
Наибольший порядок наблюдаемого спектра соответствует углу дифракции так что длина волны равна или
Подставляя это неравенство для длины волны в формулу порядка дифракционного максимума, получаем Ближайшее целое число, большее этого значения, равно 3, поэтому длина волны равна
I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом
(в данном случае - условие наблюдения главных максимумов для дифракционной решётки и анализ возможных значений порядка известного максимума):
II) описаны все вводимые в решении буквенные обозначения физических величин (за исключением, возможно, обозначений констант, указанных в варианте КИМ, и обозначений, используемых в условии задачи);
Записи, соответствующие одному или обоим пунктам: II и III, - представлены не в полном объёме или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты, не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка.
В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Ускоренная подготовка к ЕГЭ с репетиторами Учи.Дома. Записывайтесь на бесплатное занятие!

-->

Задание 7 № 28633
При нормальном падении света с длиной волны нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол (отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением Под каким минимальным углом (в градусах) можно наблюдать второй максимум на решeтке с периодом, не превосходящим 1800 нм?
Задача сводится к решению неравенства нм на интервале при заданных значениях длины волны света нм и номера максимума :

Задание 7 № 28639
При нормальном падении света с длиной волны нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом острый угол (отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением Под каким минимальным углом (в градусах) можно наблюдать третий максимум на решeтке с периодом, не превосходящим 2400 нм?
Задача сводится к решению неравенства нм на интервале при заданных значениях длины волны света нм и номера максимума :

Задание 7 № 509418
При нормальном падении света с длиной волны нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол (отсчитываемый от перпендикуляра к решетке), под которым наблюдается максимум, и номер максимума k связаны соотношением Под каким минимальным углом (в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1800 нм.
Задача сводится к решению неравенства нм на интервале при заданных значениях длины волны света нм и номера максимума :
Откуда берется k=2, если в самом задании его нет?
Второй дифракционный максимум

Задание 7 № 521991
При нормальном падении света с длиной волны на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол (отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума k связаны соотношением Под каким минимальным углом (в градусах) можно наблюдать третий максимум на решётке с периодом, не превосходящим 1950 нм?
Задача сводится к решению неравенства нм на интервале при заданных значениях длины волны света нм и номера максимума :

Задание 7 № 560776
При нормальном падении света с длиной волны нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол (отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением Под каким минимальным углом (в градусах) можно наблюдать второй максимум на решeтке с периодом, не превосходящим 1400 нм?
Задача сводится к решению неравенства нм на интервале при заданных значениях длины волны света нм и номера максимума :

Задание 7 № 28635
При нормальном падении света с длиной волны нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол (отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением Под каким минимальным углом (в градусах) можно наблюдать второй максимум на решeтке с периодом, не превосходящим 2600 нм?
Это задание ещё не решено, приводим решение прототипа.
При нормальном падении света с длиной волны нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол (отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением Под каким минимальным углом (в градусах) можно наблюдать второй максимум на решeтке с периодом, не превосходящим 1600 нм?
Задача сводится к решению неравенства нм на интервале при заданных значениях длины волны света нм и номера максимума :
При нормальном падении света с длиной волны 𝜆 = 450 нм на дифракционную решётку с периодом 𝑑 нм наблюдают серию дифракционных максимумов. При этом угол 𝜑 (отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума 𝑘 связаны соотношением 𝑑sin𝜑 = 𝑘𝜆. Под каким минимальным углом 𝜑 (в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1800 нм?
Источник: Пробный ЕГЭ 2015
Решение:
Подставим все значения в формулу и найдём 𝜑:
sinφ ≠ 0
1 – 2sinφ = 0
2sinφ = 1
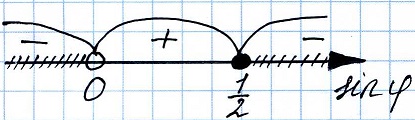
φ ∈ [30º; 150º] U (180º; 360º)
Минимальный угол φ равен 30º.
Читайте также:

