Работа при расширении газа тепловая машина коэффициент полезного действия тепловой машины
Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом . В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами .
Как следует из первого закона термодинамики, полученное газом количество теплоты полностью превращается в работу при изотермическом процессе, при котором внутренняя энергия остается неизменной ():
| . |
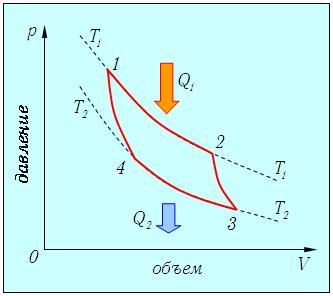
Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически . Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл , при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме () газообразного рабочего тела с помощью замкнутых кривых (рис. 3.11.1). При расширении газ совершает положительную работу , равную площади под кривой , при сжатии газ совершает отрицательную работу , равную по модулю площади под кривой . Полная работа за цикл на диаграмме () равна площади цикла. Работа положительна, если цикл обходится по часовой стрелке, и отрицательна, если цикл обходится в противоположном направлении.
Круговой процесс на диаграмме (). – кривая расширения, – кривая сжатия. Работа в круговом процессе равна площади фигуры
Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем , а с более низкой – холодильником . Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты и отдает холодильнику количество теплоты . Полное количество теплоты , полученное рабочим телом за цикл, равно
| . |
При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (). Согласно первому закону термодинамики,
| . |
Отсюда следует:
| . |
Работа , совершаемая рабочим телом за цикл, равна полученному за цикл количеству теплоты . Отношение работы к количеству теплоты , полученному рабочим телом за цикл от нагревателя, называется коэффициентом полезного действия тепловой машины:
Энергетическая схема тепловой машины: – нагреватель; – холодильник; – рабочее тело, совершающее круговой процесс. , , ;
В двигателях, применяемых в технике, используются различные круговые процессы. На рис. 3.11.3 изображены циклы, используемые в бензиновом карбюраторном и в дизельном двигателях. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (, ) и двух адиабат (, ). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (, ), одной изобары () и одной изохоры (). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.
В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке () газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру . Газ изотермически расширяется, совершая работу , при этом к газу подводится некоторое количество теплоты . Далее на адиабатическом участке () газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу . Температура газа при адиабатическом расширении падает до значения . На следующем изотермическом участке () газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре . Происходит процесс изотермического сжатия. Газ совершает работу и отдает тепло , равное произведенной работе . Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения , газ совершает работу . Полная работа , совершаемая газом за цикл, равна сумме работ на отдельных участках:
| . |
На диаграмме () эта работа равна площади цикла.
Процессы на всех участках цикла Карно предполагаются квазистатическими. В частности, оба изотермических участка (1–2 и 3–4) проводятся при бесконечно малой разности температур между рабочим телом (газом) и тепловым резервуаром (нагревателем или холодильником).
Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли его внутренней энергии. Для 1 моля газа
| , |
Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам
| . |
По определению, коэффициент полезного действия цикла Карно есть
С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя и холодильника :
Любой участок цикла Карно и весь цикл в целом может быть пройден в обоих направлениях. Обход цикла по часовой стрелке соответствует тепловому двигателю, когда полученное рабочим телом тепло частично превращается в полезную работу. Обход против часовой стрелки соответствует холодильной машине , когда некоторое количество теплоты отбирается от холодного резервуара и передается горячему резервуару за счет совершения внешней работы . Поэтому идеальное устройство, работающее по циклу Карно, называют обратимой тепловой машиной .
В реальных холодильных машинах используются различные циклические процессы. Все холодильные циклы на диаграмме () обходятся против часовой стрелки. Энергетическая схема холодильной машины представлена на рис. 3.11.5.
Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением
т. е. эфективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на затраченной работы. При таком определении может быть и больше, и меньше единицы. Для обращенного цикла Карно
Для работы любой тепловой машины по замкнутому циклу необходима внешняя среда, которую условно можно представить себе как два тела — нагреватель, находящийся при температуре Тmах, и холодильник, находящийся при температуре Tmin (Tmin < Тmах). Предполагается, что при контакте с нашей системой температуры нагревателя и холодильника не меняются. При контакте с нагревателем система получает тепло, при контакте с холодильником - отдает его.
В термодинамике существует теорема Карно (рис. 5.2):

Рис. 5.2. Леонар Сади Карно (французский физик и военный инженер)
При заданных температурах нагревателя и холодильника максимально возможный КПД тепловой машины не зависит от природы рабочего тела машины и определяется формулой
Реализация максимально возможного КПД достигается в так называемом цикле Карно, когда идеальный газ проходит замкнутый цикл, составленный из двух адиабат и двух изотерм (рис. 5.3).
Убедимся, что показанный замкнутый процесс действительно имеет КПД, соответствующий формуле (5.5). Температура системы равна T1 в точках 1, 2 и T2 в точках 3, 4. Значения остальных термодинамических параметров (р, V) будут иметь в качестве индекса номер соответствующей точки на диаграмме. Нам надо вычислить количества полученной Q1, и отданной Q2 теплоты, найти совершенную газом работу АЦ = Q1 – Q2 и определить КПД цикла. Сразу заметим, что на участках 2-3 и 4-1 система не обменивается теплом с внешней средой. Следовательно, теплоту Q1 газ получает на участке 1-2, а теплоту Q2 отдает на участке 3-4. Рассмотрим подробнее различные участки цикла.
Изотерма 1-2. На этом участке газ находится в контакте с нагревателем и происходит изотермическое расширение от объема V1 до объема V2. Температура Т1 не меняется, следовательно, не изменяется внутренняя энергия, а вся полученная теплота расходуется на совершение газом работы:
Величину работы газа при изотермическом процессе мы уже вычисляли ранее, так что с учетом формулы (2.13) находим
Адиабата 2-3. Здесь система отсоединяется от нагревателя и не обменивается теплом с внешней средой: Q23 = 0. Газ продолжает расширяться, но уже адиабатно. Работа совершается за счет внутренней энергии газа, и его температура падает до значения Т2. На этом участке цикла нам нужна информация, доставляемая уравнением адиабаты:
Изотерма 3-4. Система подключается к холодильнику, и газ начинает сжиматься. Внутренняя энергия остается неизменной, над газом совершается работа (А34 < 0), а выделяющееся
передается холодильнику. Имеем аналогично (5.6)
Адиабата 4-1. Система отключена от внешней среды и продолжает сжиматься изотермически, что приводит к повышению ее температуры до Т1. В конечном итоге система возвращается в первоначальное состояние. Поскольку точки 4 и 1 лежат на адиабате, получаем связь объемов и температур, аналогичную (5.7):
Из уравнений (5.7) и (5.9) находим отношения объемов
откуда следует, что
Поэтому отдаваемую холодильнику теплоту Q2 (см. уравнение (5.8)) можно записать как
Используя выражение (5.6) для теплоты, полученной системой, находим совершенную в ходе цикла работу
Из проведенного анализа следует также, что максимальная температура в цикле равна Тmах = Т1, а минимальная — Тmin = Т2. Если разделить (5.12) на (5.6), то немедленно получим выражение (5.5) для КПД цикла Карно, из которого выпадают все параметры, кроме температур холодильника и нагревателя.
Пример 1. Котел тепловой станции работает при температуре около t1 = 550 °С. Отработанное тепло отводится к реке при температуре около t2 = 20 °С. Найдем максимально возможный КПД этой станции (рис. 5.4).
Рис. 5.4. Схема работы тепловой машины Карно
Поскольку в формуле для КПД цикла Карно используются абсолютные температуры, надо перейти от шкалы Цельсия к шкале Кельвина: Т1 = 550 + 273 = 823 К, Т2 = 20 + 273 = 293 К. Теперь находим КПД тепловой станции:
Конечно, реальный КПД станции заметно ниже.
Если цикл Карно осуществить в обратном направлении, то есть против часовой стрелки на рис. 5.2, то для определения эффективности холодильной установки надо использовать формулы (5.3), (5.4) и выражения (5.6), (5.11). Получаем тогда
Печально, но чем ниже температура внешней среды Т1, тем меньше мы нуждаемся в холодильнике, и тем эффективнее он работает.
Рис. 5.5. Схема работы холодильной установки
Приведем численный пример. Если кондиционер поддерживает в комнате температуру t2 = 20 °С, а температура наружного воздуха равна t1 = 30 °С, то для холодильного коэффициента имеем
а для КПД холодильника
Конечно, на самом деле температура тепловыделяющего элемента больше наружной температуры на 20–30 градусов, так что разность температур может достигать 30–40 градусов, что приводит к значениям
Напомним, что речь идет об идеальных установках, работающих по циклу Карно. Реальный типичный кондиционер потребляет мощность 750 Вт, перекачивая за час около 5 МДж тепловой энергии. Это значит, что за секунду кондиционер совершает работу А = 750 Дж и отнимает у воздуха в комнате теплоту
Мы видим, что реальный кондиционер гораздо менее эффективен, нежели идеальный холодильник Карно.
Пример 2. Пусть в домашнем холодильнике поддерживается температура t2 = –3 °С (Т2 = 270 К), а температура в кухне равна t1 = 27 °С (T1 = 300 К). Пусть далее мотор холодильника потребляет мощность N = 200 Вт. Предполагая, что холодильник работает по циклу Карно и что тепловыделяющий элемент имеет температуру окружающего воздуха, определим мощность потока тепловой энергии, перекачиваемой из камеры холодильника в кухню.
За время t мотор совершит работу
КПД холодильника равен
откуда находим количество теплоты, поступающее в кухню в единицу времени:
Обратите внимание, что холодильник работает как весьма эффективный обогреватель помещения. Надо только оплачивать потребляемую мотором мощность 200 Вт, а в кухню поступит в 10 раз большая энергия, 90 % которой перекачивается из камеры холодильника (90 % — КПД холодильника в этом примере). Любопытно, что если бы вместо холодильника был включен обогреватель той же мощности, то он нагревал бы помещение в 10 раз слабее.
Наши численные оценки можно рассматривать как пример теплового загрязнения окружающей среды, свойственного технической цивилизации.
Термодинамика возникла как наука с основной задачей – созданием наиболее эффективных тепловых машин.
Тепловая машина или тепловой двигатель – это периодически действующий двигатель, совершающий работу за счет получения теплоты.
Обычно совершение работы в тепловом двигателе производится газом при его расширении. Газ, находящийся в нем, получил название рабочего тела. Зачастую его заменяют на воздух или водяные пары. Расширение газа происходит по причине повышения его температуры и давления.
Устройство, от которого рабочее тело получает тепло Q n , называю нагревателем.
Это понимается как расширение от объема V 1 к V 2 V 2 > V 1 , затем сжатие до первоначального объема. Чтобы значение совершаемой работы за цикл было больше нуля, необходимо температуру и давление увеличить и сделать больше, чем при его сжатии. То есть при расширении телу сообщается определенное количество теплоты, а при сжатии отнимается. Значит, кроме нагревателя тепловой двигатель должен иметь холодильник, которому рабочее тело может отдавать тепло.
Рабочее тело совершает работу циклично. Очевидно, изменение внутренней энергии газа в двигателе равняется нулю. Если при расширении от нагревателя к рабочему телу передается теплота в количестве Q n , то при сжатии Q ' c h теплота рабочего тела передается холодильнику по первому закону термодинамики, учитывая, что ∆ U = 0 , то значение работы газа в круговом процессе запишется как:
A = Q n - Q ' c h ( 1 ) .
Отсюда теплота Q ' c h ≠ 0 . Выгодность двигателя определяется по количеству выделенной и превращенной теплоты, полученной от нагревателя, в работу. Его эффективность характеризуется коэффициентом полезного действия (КПД), определяющимся как:
Запись уравнения ( 2 ) при учитывании ( 1 ) примет вид:
η = Q n - Q ' c h Q n ( 3 ) , КПД всегда.
Машина, отбирающая от тела с меньшей температурой определенное количество теплоты Q c h и отдающая его Q ' n телу с наиболее высокой температурой с Q ' n > Q c h , получила название холодильной машины.
Данная машина должна совершить работу A ' в течение цикла. Эффективность холодильной машины определяется по холодильному коэффициенту, вычисляемому:
a = Q ' n A ' = Q ' n Q ' n - Q c h ( 4 ) .
КПД необратимого теплового двигателя всегда меньше, чем работающего по обратимому циклу.
КПД теплового двигателя
Французским инженером Саади Карно была установлена зависимость КПД теплового двигателя от температуры нагревателя T n и холодильника T c h . Форма конструкции теплового двигателя и выбор рабочего тела не влияет на КПД идеальной тепловой машины:
η m a x = T n - T c h T n ( 5 ) .
Любой реальный тепловой двигатель может обладать КПД η ≤ η m a x .
Принцип работы теплового двигателя
Идеальная машина, модель которой разработал Карно, работает по обратимому циклу, состоящему из двух изотерм ( 1 - 2 , 4 - 3 ) и двух адиабат ( 2 - 3 , 4 - 1 ) , изображенная на рисунке 1 . В качестве рабочего тела выбран идеальный газ. Прохождение адиабатного процесса происходит без подвода и отвода тепла.

Q n = T n ( S 2 - S 1 ) ( 6 ) , где S 1 , S 2 являются энтропиями в соответствующих точках цикла из рисунка 1 .
Видно, что участок 3 - 4 характеризуется отдачей тепла холодильнику с температурой T c h идеальным газом, причем количество теплоты равняется получению газом теплоты - Q c h , тогда:
- Q c h = T c h ( S 1 - S 2 ) ( 7 ) .
Выражение, записанное в скобках в ( 7 ) , указывает на приращение энтропии процесса 3 - 4 .
Принцип действия тепловых двигателей КПД
Произведем подстановку ( 6 ) , ( 7 ) в определение КПД теплового двигателя и получаем:
η = T n ( S 2 - S 1 ) + T c h ( S 1 - S 2 ) T n ( S 2 - S 1 ) = T n - T c h T n ( 8 ) .
В выведенном выражении ( 8 ) не выполнялось предположений о свойствах рабочего тела и устройстве теплового двигателя.
По уравнению ( 8 ) видно, что для увеличения КПД следует повышать T n и понижать T c h . Достижение значения абсолютного нуля невозможно, поэтому единственное решение для роста КПД – увеличение T n .
Задача по созданию теплового двигателя, совершающего работу без холодильника, очень интересна. В физике она получила название вечного двигателя второго рода. Такая задача не находится в противоречии с первым законом термодинамики. Данная проблема считается неразрешимой, как и создание вечного двигателя первого рода. Этот опытный факт в термодинамике приняли в качестве постулата – второго начала термодинамики.
Рассчитать КПД теплового двигателя с температурой нагревания 100 ° С и температурой холодильника, равной 0 ° С . Считать тепловую машину идеальной.
Решение
Необходимо применение выражения для КПД теплового двигателя, которое записывается как:
η = T n - T c h T n .
Используя систему С И , получим:
T n + 100 ° C + 273 = 373 ( К ) . T c h = 0 ° C + 273 = 273 ( К ) .
Подставляем числовые значения и вычисляем:
η = 373 - 273 373 = 0 , 27 = 27 % .
Ответ: КПД теплового двигателя равняется 27 % .
Найти КПД цикла, представленного на рисунке 2 , если в его пределах объем идеального газа проходит изменения n раз. Считать рабочим веществом газ с показателем адиабаты γ .

Решение
Основная формула для вычисления КПД, необходимая для решения данной задачи:
η = Q n - Q ' n Q n ( 2 . 1 ) .
Получения тепла газом происходит во время процесса 1 - 2 Q 12 = Q n :
Q 12 = ∆ U 12 + A 12 ( 2 . 2 ) , где A 12 = 0 потому как является изохорным процессом. Отсюда следует:
Q 12 = ∆ U 12 = i 2 R T 2 - T 1 ( 2 . 3 ) .
Процесс, когда газ отдает тепло, обозначается как 3 - 4 , считается изохорным - Q 34 = Q ' c h . Формула примет вид:
Q 34 = ∆ U 34 = i 2 v R T 4 - T 3 ( 2 . 4 ) .
Адиабатные процессы проходят без подвода и отвода тепла.
Произведем подстановку полученных количеств теплоты в выражение для КПД, тогда:
η = i 2 v R T 2 - T 1 + i 2 v R T 4 - T 3 i 2 v R T 2 - T 1 = T 2 - T 1 + T 4 - T 3 T 2 - T 1 = 1 - T 3 - T 4 T 2 - T 1 ( 2 . 5 ) .
Следует применить уравнение для адиабаты процессу 2 - 3 :
T 2 V 1 γ - 1 = T 3 V 2 γ - 1 → T 2 = T 3 V 2 γ - 1 V 1 γ - 1 = T 3 n γ - 1 ( 2 . 6 ) .
Используем выражение для адиабаты процесса 4 - 1 :
T 1 V 1 γ - 1 = T 3 V 2 γ - 1 → T 1 = T 4 V 2 γ - 1 V 1 γ - 1 = T 4 n γ - 1 ( 2 . 7 ) .
Перейдем к нахождению разности температур T 2 - T 1 :
T 2 - T 1 = T 3 - T 4 n Г - 1 ( 2 . 8 ) .
Произведем подстановку из ( 2 . 8 ) в ( 2 . 5 ) :
η = 1 - T 3 - T 4 T 3 - T 4 n γ - 1 = 1 - 1 n γ - 1 = 1 - n 1 - γ ( 2 . 9 ) .
Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.
Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.
Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты Q полностью преобразуется в работу A в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений ( Δ U = 0 ) :
Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3 . 11 . 1 в виде диаграммы ( p , V ) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A 1 , эквивалентную площади под кривой a b c . При сжатии газ совершает отрицательную работу A 2 , равную по модулю площади под кривой c d a . Полная работа за цикл A = A 1 + A 2 на диаграмме ( p , V ) равняется площади цикла. Работа A положительна, в том случае, если цикл проходит по часовой стрелке, и A отрицательна, когда цикл проходит в противоположном направлении.

Рисунок 3 . 11 . 1 . Круговой процесс на диаграмме ( p , V ) . a b c – кривая расширения, c d a – кривая сжатия. Работа A в круговом процессе равна площади фигуры a b c d .
Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.
Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.
Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q 1 > 0 и теряет, отдавая холодильнику, количество теплоты Q 2 < 0 . Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:
Q = Q 1 + Q 2 = Q 1 - Q 2 .
Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется Δ U = 0 . Основываясь на первом законе термодинамики, запишем:
Из этого следует:
Работа A , которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты Q .
Коэффициентом полезного действия или же КПД η теплового двигателя называют отношение работы A к полученному рабочим телом за цикл от нагревателя количеству теплоты Q 1 , то есть:
η = A Q 1 = Q 1 - Q 2 Q 1 .
Рисунок 3 . 11 . 2 . Модель термодинамических циклов.
Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть ( 1 – η ) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η < 1 . На рисунке 3 . 11 . 3 проиллюстрирована энергетическая схема тепловой машины.

Рисунок 3 . 11 . 3 . Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q 1 > 0 , A > 0 , Q 2 < 0 ; T 1 >T 2 .
Виды тепловых двигателей
В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3 . 11 . 3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры ( 1 – 2 , 3 – 4 ) и две адиабаты ( 2 – 3 , 4 – 1 ) , дизельного двигателя -две адиабаты ( 1 – 2 , 3 – 4 ) , одну изобару ( 2 – 3 ) и одну изохору ( 4 – 1 ) . Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 % , у дизельного двигателя – приблизительно 40 % .
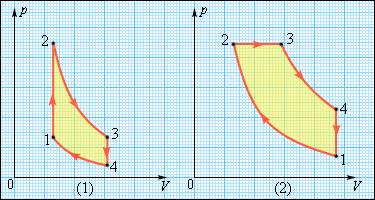
Рисунок 3 . 11 . 4 . Циклы карбюраторного двигателя внутреннего сгорания ( 1 ) и дизельного двигателя ( 2 ) .
Цикл Карно
Круговой процесс, изображенный на рисунке 3 . 11 . 5 , состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 1824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.

Рисунок 3 . 11 . 5 . Цикл Карно.
Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы ( 1 – 2 ) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T 1 . Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A 12 количество теплоты Q 1 = A 12 . После этого на участке адиабаты ( 2 – 3 ) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A 23 > 0 . Его температура при адиабатическом расширении снижается до величины T 2 . На идущем следующим участке изотермы ( 3 – 4 ) газ приводится в тепловой контакт с холодильником в условиях температуры T 2 < T 1 . Производится процесс изотермического сжатия. Газом совершается некоторая работа A 34 < 0 и отдается тепло Q 2 < 0 , эквивалентное произведенной им работе A 34 . Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T 1 , также совершается работа A 41 < 0 . совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках:
A = A 12 + A 23 + A 34 + A 41 .
На диаграмме ( p , V ) данная работа равняется площади цикла.
Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1 – 2 и 3 – 4 , относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.
Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения Δ U его внутренней энергии. Для 1 моля газа верно следующее выражение:
A = - ∆ U = - C V ( T 2 - T 1 ) ,
в котором T 1 и T 2 представляют собой начальную и конечную температуры рабочего тела.
Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:
Коэффициент полезного действия η цикла Карно может рассчитываться с помощью следующих соотношений:
η = A Q 1 = A 12 + A 34 Q 12 = Q 1 - Q 2 Q 1 = 1 - Q 2 Q 1 .
С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T 2 и нагревателя T 1 :
η = T 1 - T 2 T 1 = 1 - T 2 T 1 .
Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника:
η К а р н о = η m a x
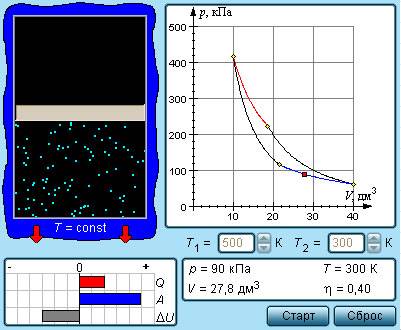
Рисунок 3 . 11 . 6 . Модель цикла Карно.
Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.
Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.
В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме ( p , V ) обходятся против часовой стрелки. На рисунке 3 . 11 . 7 проиллюстрирована энергетическая схема холодильной машины.

Рисунок 3 . 11 . 7 . Энергетическая схема холодильной машины. Q 1 < 0 , A >0 , Q 2 > 0 , T 1 > T 2 .
Работающее по холодильному циклу устройство может обладать двояким предназначением.
Если полезным эффектом является отбор некоторого количества тепла Q 2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.
Эффективность работы холодильника может быть охарактеризована следующим отношением:
Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 д ж о у л ь затраченной работы. В условиях подобного определения β х может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:
β x = T 2 T 1 - T 2 .
В случае, когда полезным эффектом является передача некоего количества тепла
| Q 1 | нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.
Эффективность β Т теплового насоса может быть определена с помощью отношения:
То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 д ж о у л ь затраченной работы. Из первого закона термодинамики следует:
Следовательно, β Т всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение:
Читайте также:

