Показатель лямбда для эквивалентной функции
Крамера и коэффициентом "лямбда". [c.552]
Мы рассмотрим статистики, обычно используемые для оценки статистической значимости и тесноты связи переменных, в таблице сопряженности. Статистическая значимость наблюдаемой связи обычно измеряется критерием Теснота связи важна с практической точки зрения. Обычно она имеет значение, если связь статистически значимая. Тесноту связи можно измерить коэффициентом корреляции фи, коэффициентом сопряженности Крамера и коэффициентом "лямбда". Эти статистики ниже описаны детальнее. [c.575]
Таким образом, связь не очень сильна. В этом случае V = о Так всегда происходит для таблицы Другой обычно рассчитываемой статистикой является коэффициент "лямбда". [c.578]
Мера в процентах улучшения прогнозирования значения зависимой переменной при данном значении независимой переменной. Значения коэффициента "лямбда" лежат в пределах от 0 до [c.578]
Значения коэффициента "лямбда" лежат в пределах от 0 до 1. Значение "лямбда", равное О, означает, что никакого улучшения в прогнозировании не наблюдается. Значение 1 указывает на то, что прогноз может быть сделан без ошибки. Это происходит тогда, когда каждая категория независимой переменной связана с одной категорией зависимой [c.579]
Симметричный коэффициент "лямбда" не дает предположения о какая из переменных зависимая. Он измеряет общее улучшение прогнозирования, когда прогноз уже сделан в обоих направлениях. [c.579]
Если нулевая гипотеза отклонена, то определите тесноту связи, используя статистики коэффициент сопряженности, Крамера, коэффициент "лямбда" или другие статистики). [c.580]
Л (лямбда) - коэффициент Оукена [c.830]
Коэффициент "лямбда" используется в том случае, когда переменные измерены с помощью номинальной шкалы, коэффициент (asymmetri lambda) показывает выраженное в процентах улучшение при прогнозировании значения зависимой переменной при данном значении независимой переменной, [c.578]
Асимметрический коэффициент "лямбда" подсчитывают для каждой из зависимых переменных. Также рассчитывают симметричный коэффициент (symmetri lambda) — средним значением двух асимметричных значений. [c.579]
Симметричный коэффициент "лямбда" не делает предположения о том, какая из переменных зависимая. Он измеряет прогнозирования, когда прогноз уже выполнен в обоих направлениях [14]. Значение асимметричного коэффициента "лямбда" в табл. 15.3, если в качестве переменной взять Internet, равно 0,333. Это указывает на то, что знание пола нашу возможность прогнозирования на 0,333, т.е. имеет место улучшение прогнозирования на 0,33%. Симметричный коэффициент "лямбда" также равен 0,33%. [c.579]
Часто, чтобы лучше уяснить суть связи переменных, вводят третью переменную. Статистика позволяет проверить статистическую значимость наблюдаемой в таблице, s o-i-i пряженности. С помощьюкоэффициента сопряженности, V -коэффициент Крамера и коэффициента "лямбда" определяют силу связи между переменными. [c.598]
Бессмысленно интерпретировать результаты анализа, если определенные дискрими-не являются статистически значимыми. Поэтому выполнить статистическую проверку нулевой гипотезы о равенстве средних всех функций во всех группах генеральной совокупности. В программе SPSS эта проверка базируется на коэффициенте лямбда (X) Уилкса. Если одновременно проверяют несколько [c.695]
Измерители линейной чувствительности к движению финансовых переменных используются под различными обозначениями. На рынке инструментов с фиксированным доходом чувствительность к движению процентных ставок измеряется дюрацией. На рынке акций чувствительность к фактору рынка в цепом (например, фондовому индексу) называется систематическим риском или коэффициентом бета. На рынке производных инструментов чувствительность

Я решил написать эту серию статей, ибо считаю, что никто не должен сталкиваться с той стеной непонимания, с которой столкнулся когда-то я.
Ведь большинство статей написаны таки образом что, для того чтобы понять что-то в Функциональном Программировании (далее ФП), тебе надо уже знать многое в ФП. Эту статью я старался написать максимально просто — настолько понятно, чтобы её суть мог уловить мой племянник, школьник, который сейчас делает свои первые шаги в Python.
Небольшое введение
- Чистая Функция
- Функции высшего порядка
Чистая Функция — Функция которая является детерминированной и не обладает никакими побочными эффектами.
То есть чтобы функция являлась чистой она должна быть детерминированной — то есть каждый раз при одинаковом наборе аргументов выдавать одинаковый результат.
Пример детерминированной функции
И пример не детерминированной:
Каждый раз при смене дня недели (который не является аргументом функции) функция выдает разные результаты.
Самый очевидный пример не детерминированной функции это random:
Второе важное качество чистой функции это отсутствие побочных эффектов.
Функция sort_by_sort имеет побочные эффекты потому что изменяет исходный список элементов и выводит что то в консоль.
В отличии от предыдущего примера функция sort_by_sorted не меняет исходного массива и возвращает результат не выводя его в консоль самостоятельно.
Чистые функции хороши тем что:
- Они проще читаются
- Они проще поддерживаются
- Они проще тестируются
- Они не зависят от того в каком порядке их вызывать
Функции высшего порядка — в программировании функция, принимающая в качестве аргументов другие функции или возвращающая другую функцию в качестве результата.
С основами чуть чуть разобрались и теперь перейдем к следующему шагу.
Итак, начнем
Для начала надо понять следующее — что такое Функциональное Программирование вообще. Лично я знаю две самые часто упоминаемые парадигмы в повседневном программировании — это ООП и ФП.
Если упрощать совсем и объяснять на пальцах, то описать эти две парадигмы можно следующим образом:
- ООП — это Объектно Ориентированное Программирование — подход к программированию, при использовании которого объекты можно передавать в качестве параметров и использовать их в качестве значений.
- По такой логике можно установить, что ФП — подход к программированию, при использовании которого функции можно передавать другим функциям в качестве параметров и использовать функции в качестве значений, возвращаемых другими функциями… Ответ скрыт в самом названии.
Это относится и к ФП — взял какие-то данные, взял какую-то функцию, поигрался с ними и выдал что-то на выходе.
Не стану расписывать всё, иначе это будет оооочень долго. Цель данной статьи — помочь разобраться, а не объяснить, как и что работает, поэтому тут мы рассмотрим основные функции из ФП.
В большинстве своем ФП (как я его воспринимаю) — это просто упрощенное написание кода. Любой код, написанный в функциональном стиле, может быть довольно легко переписан в обычном стиле без потери качества, но более примитивно. Цель ФП заключается в том, чтобы писать код более простой, понятный и который легче поддерживать, а также который занимает меньше памяти, ну и куда же без этого — разумеется, главная вечная мораль программирования — DRY (Don’t Repeat Yourself — Не повторяйся).
Сейчас мы с вами разберем одну из основных функций, которая применяется в ФП — Lambda функцию.
В следующих статьях мы разберем такие функции как Map, Zip, Filter и Reduce.
Lambda функция
Lambda — это инструмент в python и других языках программирования для вызова анонимных функций. Многим это скорее всего ничего не скажет и никак не прояснит того, как она работает, поэтому я расскажу вам просто механизм работы lambda выражений.
Все очень просто.
Рассмотрим пример. Например, нам надо написать функцию которая бы считала площадь круга при известном радиусе.
Формула площади круга это
где
S — это площадь круга
pi — математическая константа равная 3.14 которую мы получим из стандартной библиотеки Math
r — радиус круга — единственная переменная которую мы будем передавать нашей функции

Теперь оформим это все в python:
Вроде бы неплохо, но это всё может выглядеть куда круче, если записывать это через lambda:
Чтобы было понятнее, анонимный вызов функции подразумевает то, что вы используете её, нигде не объявляя, как в примере выше.
Лямбда функция работает по следующему принципу
Рассмотрим пример с двумя входными аргументами. Например, нам надо посчитать объем конуса по следующей формуле:

Запишем это все в python:
А теперь как это будет выглядеть в lambda форме:
Количество переменных здесь никак не ограничено. Для примера посчитаем объем усеченного конуса, где у нас учитываются 3 разные переменные.
Объем усеченного конуса считается по формуле:
И вот, как это будет выглядеть в python классически:
А теперь покажем, как это будет выглядеть с lambda:
После того, как мы разобрались, как работает lambda функция, давайте разберем ещё кое-что интересное, что можно делать с помощью lambda функции, что может оказаться для вас весьма неожиданным — Сортировку.
Сортировать одномерные списки в python с помощью lambda довольно глупо — это будет выглядеть, как бряцание мускулами там, где оно совсем не нужно.
Ну серьезно допустим, у нас есть обычный список (не важно состоящий из строк или чисел) и нам надо его отсортировать — тут же проще всего использовать встроенную функцию sorted(). И в правду, давайте посмотрим на это.
В таких ситуациях, действительно, хватает обычного sorted() (ну или sort(), если вам нужно изменить текущий список на месте без создания нового, изменив исходный).
Но что, если нужно отсортировать список словарей по разным ключам? Тут может быть запись как в классическом стиле, так и в функциональном. Допустим, у нас есть список книг вселенной Песни Льда и Пламени с датами их публикаций и количеством страниц в них.
Как всегда, начнем с классической записи.
А теперь перепишем это все через lambda функцию:
Таким образом, lambda функция хорошо подходит для сортировки многомерных списков по разным параметрам.
Если вы повторите весь этот код самостоятельно, написав его сами, то я уверен, что с этого момента вы сможете сказать, что отныне вы понимаете, как работают lambda выражения, и сможете применять их в работе.
Но где же тут та самая экономия места, времени и памяти? Экономится максимум пара строк.
Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.
Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…
λ-исчисление: основные понятия
Синтаксис
В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.
Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.
Термы:
| переменная: | x |
| лямбда-абстракция (анонимная функция): | λx.t , где x — аргумент функции, t — её тело. |
| применение функции (аппликация): | f x , где f — функция, x — подставляемое в неё значение аргумента |
- Применение функции левоассоциативно. Т.е. s t u — это тоже самое, что (s t) u
- Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е. λx. λy. x y x означает то же самое, что λx. (λy. ((x y) x))
- Скобки явно указывают группировку действий.
Процесс вычисления
Рассмотрим следующий терм-применение:
Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:
который для простоты можно переписать как
(напомним, что id — это функция тождества вида λx.x )
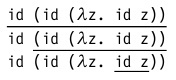
В этом терме содержится три редекса:
Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение
(λx.λy. x) z ((λx.x x)(λx.x x))
Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y . Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y , а z — первоначальный терм имел бы вид (λx.λz.x)y и после редукции выглядел бы как λz.y . Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.
Так же бывает, что у нас есть абстракция λx.t x , причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t . Такое преобразование называется η-конверсией.
На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Конечно многие из нас знакомы с этим понятием, однако данная статья рассчитана на новичков. В данном посте постараюсь рассмотреть данный феномен и привести примеры использования. Для начала необходимо понять что же такое лямбда-функция. Итак, лямбда-функция, часто ее называют анонимной, т. е. функция при определении которой не нужно указывать ее имя. Возвращаемое значение такой функцией присваивается переменной, через которую в последствие эту функцию можно вызывать.
До выхода PHP 5.3 определять лямбда-функции было возможно, но их нельзя было назвать полноценными. Сейчас я приведу пару примеров и продолжим рассматривать данные понятия.
Конечно динамическое создание функций не решает всех проблем, однако порой написание такой одноразовой функции может быть полезным. Можно расширить наш пример:
Понятие замыкания наверняка знакомо программистам на JavaScript, а так же программистам на многих других языках. Замыкание — это функция, охватывающая или замыкающая текущую область видимости. Что бы понять все это, рассмотрим пример:
Как вы уже могли заметить, функция не имеет имени и результат присваивается переменной. Лямбда-функция, созданная таким образом, возвращает значение в виде объекта типа closure.
В PHP 5.3 стало возможно вызывать объекты как если бы они были функциями. А именно магический метод __invoke() вызывается каждый раз, когда класс вызывается как функция.
Переменные недоступны внутри функции, если они не объявлены глобальными, так же переменные из дочернего контекста недоступны если только не используется зарезервированное слово use. Обычно в PHP переменные передаются в замыкание значением, это поведение можно изменить с помощью ампермсанда перед переменной в выражении use. Рассмотрим пример:
Если убрать амперсанды то оба раза выведется 80, т. к. переменная $mul внутри замыкания будет копией, а не ссылкой.
Итак, осталось только выяснить как это можно применить на практике.
Рассмотрим пример:
Этот пример уже можно использовать для достаточно гибкого прототипирования. Достаточно объявить методы для всех SQL-операций с объектом.
Автор не призывает всех придерживаться такой практики, равно как и не считает что так лучше, все вышеописанное лишь пример использования, причем возможно не самый техничный и интересный, и не более того.
UPD Говоря о том самом длинном регулярном выражении, я не стал подписывать его в комментариях и решил вынести сюда. Оно лишь ищет строки в одинарных и двойных кавычках, а так же имена таблиц и экранирует их.





4 14
4 14
В Torque параметра Commanded Equivalence Ratio (lambda), не нашёл. Есть параметр Заданное эквивалентное соотношение (Лямбда), которое всегда равно 1.
По программе CarScanner показания ДК1 следующие. При резком нажатии педали газа, подпрыгивает до 0.85-0.9 V. При резком отпускании педали газа, кратковременно может упасть до 0 V. На холостом и при удержании оборотов на одном уровне, напряжение скачет от 0.1 до 0.7 V.
Подскажите пожалуйста, период колебаний верхнего лямбда в три секунды на холостых это не слишком много, это не говорит о том что датчик подызносился?
281
А при чём тут ДК? С ним как раз всё в порядке, если канеш, эта осциллограмма не анимация. Изменение напряжения на ДК показывает не как быстро реагирует датчик на изменение смеси, а как быстро меняется состав смеси сгоревших газов. Электрический сигнал проходит моментально, а вот изменение выхлопа растянуто по времени.

Затупил немного. начитался где-то, что период должен быть около секунды, а это на оборотах около 2000 период секунда или чуть меньше, так что у меня все нормально.
281
Более того, я бы сказал, что эти осциллограммы уж очень похожи на эталонные. Я вам по-доброму завидую. Если это с вашего автомобиля, то будьте горды состоянием выхлопа вашего автомобиля и получайте удовольствие и дальше!

17 21
Добрый день. Посмотрите, плиз, на дк1 и дк2. Немного пред истории: Выбил кат ( на пробеге 120 т. к, из-за боязни осыпания и всасывании пыли в цилиндры), установил пламик и самую простую обманку. После этого увеличился расход горючки и авто стало подтупливать. При разгоне на 1-й передаче ускоряется норм до 2000 оборотов, потом провал секунды на 3 ( как будто за попу кто-то держит). После набора оборотов до 3000 машина подрывается. Смотрю на дк1 и смущает маленький размах синусоиды примерно 0.5-0.6 ( от 0.1 до 0.7 максимум) очень редко размах проскакивает до от 0.1 до 0.8. Може быть устал дк1. И еще, дк2 учавствует хоть как нибудь в образовании топливо-воздушной смеси? Или он только за состоянием ката наблюдает? Обманка не справляется. На ХХ вроде что-то похоже на правду, а вот на нагрузке нагрузке дк2 начинает повторять дк1. Ошибок никаких нет. Двиг. G4FC. Фото 1 - ХХ. Фото 2 - 2700 об.
Читайте также:

