Лямбда функция в маткаде

Обновлено: 26.01.2025

Функции в Mathcad

Произвольные зависимости между входными и выходными параметрами задаются при помощи функций. Функции принимают набор параметров и возвращают значение, скалярное или векторное (матричное). В формулах рабочего листа можно использовать стандартные встроенные функции, а также функции, определенные пользователем.

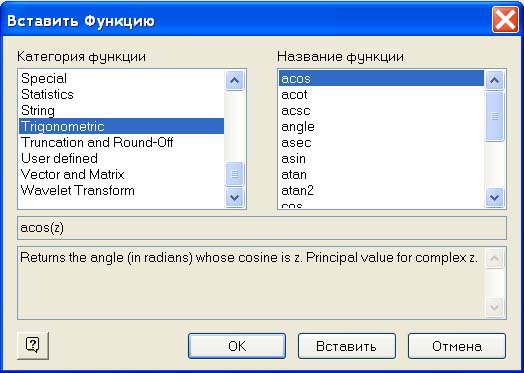
Чтобы использовать функцию в выражении, ее следует вызвать по имени, указав в значения фактических входных параметров в скобках после имени функции. Имена простейших математических функций можно ввести с панели инструментов Калькулятор (Arithmetic). Информацию о других функциях можно почерпнуть в справочной системе или в приложении. Вставить в выражение стандартную функцию можно при помощи команды Вставка > Функция (Insert > Function). В диалоговом окне (рис. 1.9) слева выбирается категория, к которой относится функция, а справа – конкретная функция. В нижней части окна выдается информация о выбранной функции. При вводе функции через это диалоговое окно автоматически добавляются скобки и заполнители для значений параметров.

Пользовательские функции должны быть сначала определены. Определение задается при помощи оператора присваивания. В левой части указывается имя пользовательской функции и, в скобках, формальные параметры – переменные, от которых она зависит. Справа от знака присваивания эти переменные должны использоваться в выражении, например

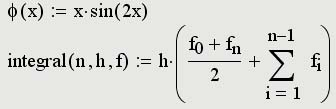
Если для вычисления пользовательской функции необходимо выполнить несколько операций, то в теле функции формируют необходимое число строк с помощью кнопки Add line панели Программирование и в появившиеся заполнители помещают формулы. Отметим, что в операторах тогда допустима операция внутреннего присваивания, задаваемая стрелкой, а все вычисленные подобным образом переменные являются локальными и за пределами функции будут не определенны. Так, на рис. 1.10 функция fct вычисляется за три действия, а переменные с_2k и c_3k будут видимыми только внутри функции.

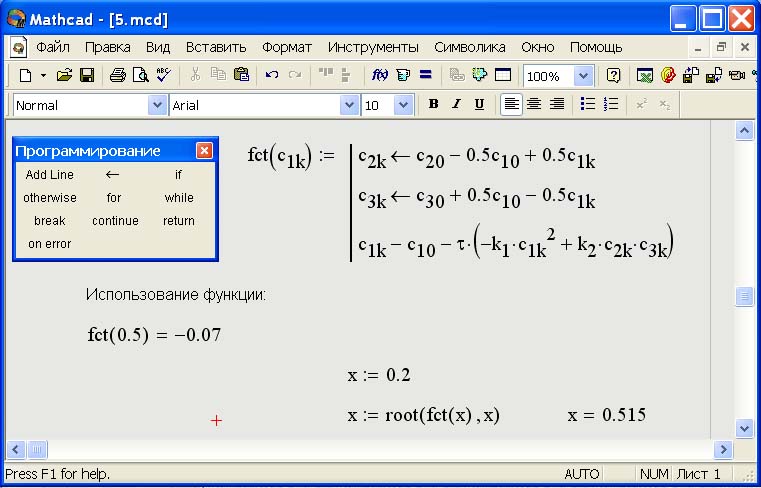
При применении пользовательской функции в последующих формулах ее имя вводят вручную. В диалоговом окне Вставка функции оно не отображается.

Аналитические вычисления в Mathcad

С помощью аналитических вычислений находят аналитические или полные решения уравнений и систем, вычисляют в производные и неопределенные интегралы, а также проводят преобразования сложных выражений (например, упрощение). Иначе говоря, при таком подходе можно получить результат в виде некоторой функции. В программе Mathcad при проведении символьных преобразований конкретные значения, присвоенные переменным, игнорируются – переменные рассматриваются как неопределенные параметры.

Для проведения таких символьных операций, как вычисление производной или интеграла можно набрать выражения с помощью панели Исчисление (рис. 1.15) или "горячих" клавиш, описанных в приложении, и затем использовать оператор вычисления в символьном виде "" панели Символика (рис. 1.16):

; сравните:

Команды для выполнения аналитических вычислений в основном сосредоточены в меню Символика (Symbolics) и продублированы на аналогичной панели инструментов.

Чтобы упростить выражение (или часть выражения), надо выбрать его при помощи уголкового курсора и дать команду Символика > Упростить (Symbolics > Simplify). При этом выполняются арифметические действия, сокращаются общие множители и приводятся подобные члены, применяются тригонометрические тождества, упрощаются выражения с радикалами, а также выражения, содержащие прямую и обратную функции. Некоторые действия по раскрытию скобок и упрощению сложных тригонометрических выражений требуют применения команды Символика > Раскрыть/Расширить (Symbolics > Expand).

В меню Символика (Symbolics) предусмотрен ряд операций, ориентированных на выделенную переменную, использованную в выражении. Например, команда Solve (Решить) ищет корни функции, заданной данным выражением. В примере в аналитической форме получены все корни полинома второй степени: сначала применена команда solve для решения, а затем simplify для упрощения результата:

Другие возможности использования этого меню включают:

пример:
– исходное выражение:
– результат дифференцирования по х:
– результат интегрирования по х:

пример:
– исходное выражение:
– в буфер обмена скопировано выражение:
– результат замены переменной х:

Механизм аналитических вычислений можно использовать для аналитического решения уравнений и систем уравнений и неравенств. Для этого задается блок решения Given, в который помещаются уравния и неравенства, а последняя формула блока должна выглядеть как

Find(х,у. ),

где в скобках приведен список искомых величин, а далее следует знак аналитического вычисления, отображаемый в виде стрелки, направленной вправо:

пример:
– начало блока:
– решаемое уравнение:
– поиск решения по х:

Отметим, что функция Find пытается найти решение в аналитической форме. В том случае, если до блока Given задать численно значения всех параметров, входящих в уравнения, а также начальные приближения для корней, то получим решение в числовом виде.

Примеры использования функции Find для решения уравнений и систем уравнений различного типа приведены в соответствующих разделах пособия.

Любое аналитическое вычисление можно применить с помощью ключевого слова. Cписок ключевых слов приведен в приложении.

Ошибка - это значение должно быть массивом
задание:необходимо определить координаты поворотных точек относительно начала маршрута. дано.

Значение должно быть массивом
Добрый вечер! Очень нужна Ваша помощь (цикл в этой задаче помогали задавать на Вашем форуме, за что.

Значение должно быть массивом
Здравствуйте! Просьба помочь создать 3д-график решения уравнения теплопроводности. Что нужно.

Значение должно быть массивом, переменная не определена
При построении графика появляются ошибки - значение должно быть массивом, переменная не определена.

У Вас наложение двух ошибок: 1) при задании значения лямбда Mathcad сообщает о неизвестной функции Х(), после замены на лямбда=1, он сообщает о неправильном вызове функции f(x,y), потому что Вы её переопределили на другую справа в верхнем углу. Я перенёс описания этих функций вниз, после этого произошёл следующий вывод grad

Решение

И снова здравствуйте!Вопрос в следующем программа grad у меня формирует функцию FF(лямбда) .Нужно чтобы программа XX использовала эту сформированную функцию,т е брала это сформированную функция из программы grad и вычисляла лямбда.Возможно ли это сделать в маткаде?

Решение

Подпрограмму-функцию XX() лучше оставить отдельной, просто добавив в список её аргументов функцию FF, которая переопределяется внутри процедуры-функции grad():

Ошибка - значение должно быть скалярным
Помогите, пожалуйста. Необходимо решить ду первого порядка. Выдает ошибку-"значение должно быть.

Ошибка: значение должно быть скалярным
есть численное значение,которое я задаю,но маткад говорит что значение должно быть скалярным,хотя.

Ошибка: значение должно быть скалярным
Дан АМ-сигнал. Нужно найти его спектральную плотность, но сначала я нахожу спектральную плотность.

Ошибка - значение должно быть функцией
Не могу понять где у меня ошибка (Значение должно быть функцией, но имеет форму: any1.) Подскажите.

Ошибка: значение должно быть скалярным
Возникает такая проблема, не нашел решение в интернете Вот файлы

Известно, что в Mathcad`е нельзя построить график неявно заданной функции встроенными средствами самого матпакета.Однако, мпрограммно-можно.Вот пример построения графика методом "марширующего квадрата".
На картинке изображены только стороны квадрата, которые пересекают график функции.
Причем квадрат именно"шагает" по кривой графика, никакой сетки нет.

График функции, заданной неявно
Есть функция (фото) и не получается задать в маткаде ее в таком виде, как сказано в задании (в.

Построить график неявно заданной функции
Дана функция x^2*y^2-x^3+y^3. Необходимо построить её график. Вроди как её сделал, но не уверен в.

Построить график функции в Маткаде (конхоида Никомеда)
Здравствуйте. Необходимо построить гр. ф-ции выражения: В задании сказано: продемонстрировать.

Квадрат шагает по непрерывной кривой и перескакивать с одной кривой на другую не может.
Если ему задать по одной точке на каждой кривой, то он построит так же как Мaple и программа Мезенцева.
Я задал ему одну точку- он одну кривую и построил.
Maple и Мезенцев используют сетку и их программы сканируют всю область (каждую клетку).
Здесь же - квадрат двигается строго по кривой.

Неявные кривые может строить GeoGebra и она бесплатна.
А вообще алгоритмы рисования в Mathcad, Mathematica, Maple, SMAth похоже софтверные, через процессор. Отсюда сильные тормоза в расчете, это из-за низкого уровня программистов их создавших.Вообще странно, что люди с их уровнем математики так нелепо сделали софтверный рендер. Когда-то даже рисовал не неявные, а даже просто пути из кривых Безье, при этом маткад жутко тормозил. В GeoGebre было быстрей.

А изоповерхности для маткада вообще тяжелые, а вот в k3dsurf строит их и поворачивает намного быстрей(использует OpenGL)… но там нельзя менять порог поля.

Не строится график заданной функции
Помогите, пожалуйста, вообще не строится график функции. Выводит комплексные числа, не знаю, как.

Построить график параметрически заданной функции.
построить график параметрически заданной функции при значениях констант a,b и лямда. фи меняется от.

Построить график параметрически заданной функции
Построить график параметрически заданной функции при значениях конcтант а, b,\lambda . Оси.

График ДУ в Маткаде
Мне необходимо решить ДУ Коши 2 способами - "ручным" и в Маткаде. Стандартным способом я его решил.

Рассмотрим некоторые стандартные функции системы MathCAD. Введем специальные обозначения для аргументов функций. Пусть первый символ имени аргумента обозначает его тип:

M – квадратная матрица;

V – вектор (матрица из одного столбца);

A – произвольная матрица;

S – симметричная матрица;

G – произвольная матрица или число;

X – вектор или число;

Z – комплексная матрица или число;

z – комплексное число;

прочие символы – скалярные величины.

Экспоненциальные и логарифмические функции

exp(X) – экспонента от X;

ln(X) – натуральный логарифм от X;

log(X) – десятичный логарифм от X;

log(X,b) – логарифм от X по основанию b.

Гиперболические и тригонометрические (прямые и обратные) функции

sin(X), cos(X), tan(X), cot(X), sec(X), csc(X) – соответственно синус, косинус, тангенс, котангенс, секанс, косеканс от X, причем аргументы указываются в радианах;

sinh(X), cosh(X), tanh(X), coth(X), sech(X), csch(X) – аналогичные гиперболические функции;

asin(z), acos(z), atan(z), acot(z), asec(z), acsc(z) – соответственно арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс от z.

Функции для работы с комплексными числами

Re(Z), Im(Z) – соответственно вещественная и мнимая части комплексного числа Z;

arg(z) – аргумент комплексного числа z (в радианах).

length(V) – возвращает число элементов вектора V;

cols(A) – возвращает число столбцов матрицы A;

rows(A) – возвращает число строк матрицы A;

matrix(m, n, f) – матрица размером mxn, значения элементов матрицы определяются f – функцией f (i, j) от двух переменных (номера строки и номера столбца). Эта функция должна быть предварительно определена пользователем;

identity(n) – единичная матрица n×n;

tr(M) – след матрицы M (сумма элементов главной диагонали);

rank(A) – ранг матрицы M;

norme(M) – эвклидова норма матрицы M, то есть корень квадратный из суммы квадратов всех элементов;

eigenvals(M) – вектор, элементы которого являются собственными числами матрицы M;

eigenvecs(M) – матрица, состоящая из нормализованных собственных векторов матрицы M;

cholesky(S) – возвращает нижнетреугольную матрицу L – результат разложения Холецкого вида L∙LT = S;

lu(M) – возвращает матрицу размера n×3n, состоящую из трех соединенных матриц P, L, U, являющихся результатом LU-разложения вида P∙M = L∙U.

Пример вычислений с матричными функциями: нахождение собственного числа путем решения матричного уравнения det(M – λE) = 0 и с помощью функции eigenvals.

Элементы статистического анализа данных

gmean(G1,G2,G3…) – среднее геометрическое аргументов;

mean(G1,G2,G3…) – среднее арифметическое аргументов;

stdev(G1,G2,G3…) – среднеквадратичное отклонение.

fft(V1), ifft(V2) – прямое и обратное быстрые преобразования Фурье над вещественными данными. V1 – вектор из 2m элементов, V2 – вектор из 1 + 2m–1 элементов, m > 2;

cfft(A), icfft(A) – прямое и обратное преобразования Фурье над вещественными и комплексными векторами и матрицами;

wave(V), iwave(V) – прямое и обратное вейвлет-преобразования, V – вектор из 2m элементов, m – целое число.

Аппроксимация, интерполяция и экстраполяция

Аппроксимация – поиск функции, которая с заданной степенью точности описывает исходные данные.

Интерполяция – определение наиболее правдоподобных промежуточных значений в интервале между известными значениями (подбор гладкой кривой, проходящей через заданные точки или максимально близко к ним).

Экстраполяция – определение наиболее правдоподобных последующих значений на основании анализа предыдущих значений (предсказание дальнейшего поведения неизвестной функции).

Применяются следующие функции MathCAD:

regress(VX,VY,k) – возвращает вектор данных, используемый для поиска интерполирующего полинома (a0 + a1x + a2x2 + . + akxk) порядка k. Полином должен описывать данные, состоящие из упорядоченных значений аргумента (VX) и соответствующих значений неизвестной функции (VY), то есть график полинома должен проходить через все точки, заданные координатами (VX, VY), или максимально близко к этим точкам;

interp(VS,VX,VY,x) – возвращает интерполированное значение неизвестной функции при значении аргумента x. VS – вектор значений, который вернула функция regress. VX,VY – те же данные, что и для regress. Функции interp и regress используются в паре;

predict(V,m,n) – возвращает вектор из n предсказанных значений на основании анализа m предыдущих значений из вектора V. Предполагается, что значения функции в векторе V были получены при значениях аргумента, взятых последовательно, с одинаковым шагом. Используется алгоритм линейной предикции. Наиболее целесообразно использовать predict для предсказания значений по данным, в которых отмечены колебания.

Для интерполяции система MathCAD использует подход, основанный на применении метода наименьших квадратов.

Примеры интерполяции и экстраполяции:

1.5.1. Пусть заданы координаты пяти точек (1; 1), (2; 2), (3; 3), (4; 2), (5; 3), представляющих результаты измерения значений некоторой неизвестной функции при различных значениях x. Необходимо подобрать интерполирующую функцию (гладкую кривую), проходящую через заданные точки.

1.5.2. Дана функция y(i) = e–i/10∙sin (i). Известны значения данной функции при i = 0, 1, …, 10. Основываясь на десяти последних значениях, необходимо предсказать последующие десять значений.

Решения показаны на рис. 19.

Рис. 19. Решения в MathCAD первой (а) и второй (б) задач

Нахождение корней полинома

polyroots(V) – возвращает вектор, содержащий все корни полинома a0 + a1x + a2x2 + . + akxk, заданного вектором-столбцом коэффициентов

Читайте также: