Газодинамическая функция q от лямбда

Обновлено: 26.01.2025

Мы выяснили, что скорость истечения газов зависит не только от π_с (p_с, ) и , но и от формы сопла. Форма сопла должна быть не цилиндрической трубой, а специально спрофилированной. В таком сопле при изменении скорости происходит одновременное изменение параметров состояния газа.

Для расчёта изменения параметров газа при его движении в каналах, в том числе и соплах, в газовой динамике широко используются газодинамические функции (приведенные параметры или относительные параметры). Газодинамические функции представляют собой отношения действительных (статических) параметров в любом сечении потока к значению тех же параметров заторможенного потока, в каком либо другом, сравнительном сечении.

Таким образом, значение параметра в сравнительном сечении является как бы мерой, масштабом для значения данного параметра во всех других сечениях.

В расчётной практике сложилась традиция брать в качестве масштабов для одних величин значения параметров торможения, для других – значения критических параметров.

Главную роль при расчётах играют следующие газодинамические функции:

– плотности тока газа ; (8.41)

Газодинамическая функция q (λ) имеет важное значение в термодинамике газового потока, так как она характеризует расход газа.

Число Маха представляет собой безразмерную (относительную) скорость потока, причём масштабом скорости здесь является местная скорость звука а.

Все газодинамические функции являются безразмерными параметрами потока. Газодинамические функции позволяют значительно облегчить проведение расчётов авиационных ГТД. Значение этих функций обычно представляются в виде таблиц (смотри приложение П.4), где аргументом выступает коэффициент скорости λ или её называют приведённой скоростью.

Коэффициент скорости λ – отношение действительной скорости потока в любом рассматриваемом сечении потока (с_х) к значению критической скорости (с_кр).

где Т * вычисляется в точке потока к которой относится скорость с.

В формулах (8.43), (8.43') масштабом скорости принимается критическая скорость.

Коэффициент скорости λ имеет вполне конкретные значения. Найдём их. Скорость газа с при его движении по соплу может теоретически изменяться от нуля до с_кр, а потом достигнуть с_max. Критическая скорость с_кр для данного газа при = const является величиной постоянной, следовательно коэффициент скорости λ может принимать значения от λ = 0 до λ = λ_max, так как при значении

с_х = 0, λ = 0;

Определим значения λ_max для воздуха, для которого k = 1,4; R = 287 Дж / (кг ∙ К).

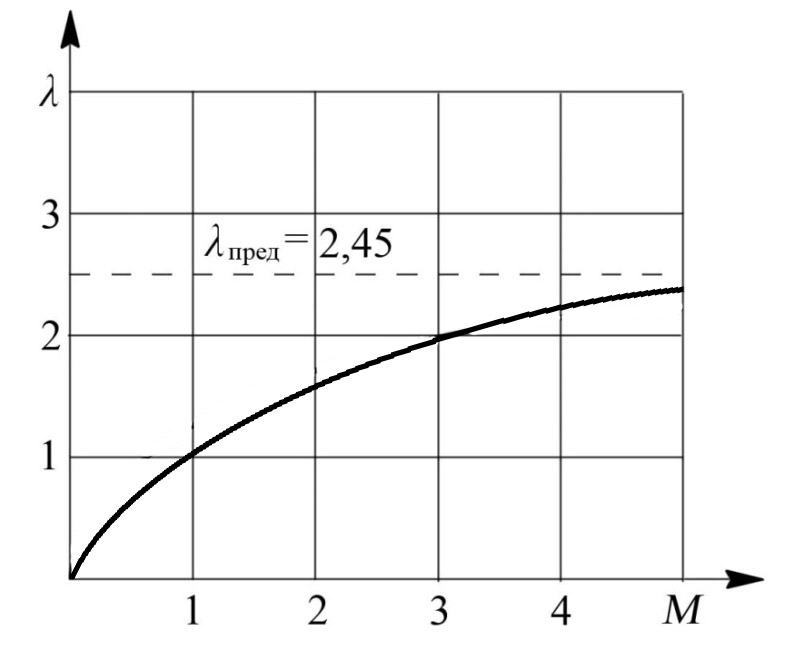
З ависимости скорости потока от коэффициента скорости и зависимости λ = f (M) показаны соответственно на рис. 8. 9. и рис. 8.10.

Рис. 8.9. График зависимости λ = f (M) для k = 1,4; R = 287 Дж / (кг ∙ К)

Таким образом, коэффициент скорости λ для воздуха может иметь конкретные числовые значения

Рис. 8.10. График зависимости с = f (λ) для k = 1,4; R = 287 Дж / (кг ∙ К)

Поэтому газодинамические функции выражают через коэффициент скорости. Получим формулы для вычисления газодинамических функций

После преобразования (8.45) получим газодинамическую функцию температуры, где аргументом выступает коэффициент скорости λ, т. е.

Далее используя адиабатные зависимости между параметрами состояния газа, можно получить газодинамические функции давления и плотности

Используя известные формулы, можно выразить через коэффициент скорости и другие газодинамические функции.

Преобразуем (8.41) и получим газодинамическую функцию плотности тока газа

Величина q (λ) связана с расходом газа следующим образом:

Газодинамическая функция сжимаемости М однозначно связана с коэффициентом скорости λ. Действительно

Построим график изменения функций τ, π, ε, q в зависимости от λ для воздуха (k =1,4; λ_max = 2,45), используя уравнения (8.46; 8.47; 8.48; 8.49) и подставив в них значения λ = 0; λ = 1; λ = λ_max. В результате получим:

при λ = 0 → τ (λ) = π (λ) = ε (λ) = 1; q (λ) = 0

при λ = 1 → τ (λ) = 0,833; π (λ) = 0,528; ε (λ) = 0,634; q (λ) = 1

при λ = λ_max = 2,45 → τ (λ) = π (λ) = ε (λ) = q (λ) = 0.

Полученные результаты используем для построения графиков газодинамических функций, которые приведены на рис. 8.11.

Этими графиками можно пользоваться только для решения задач, не требующих высокой точности расчёта. Для более точных расчётов следует использовать таблицы газодинамических функций, в которых приводятся значения функций от λ с точностью до 5 – 7-го знака (Приложение П.4).

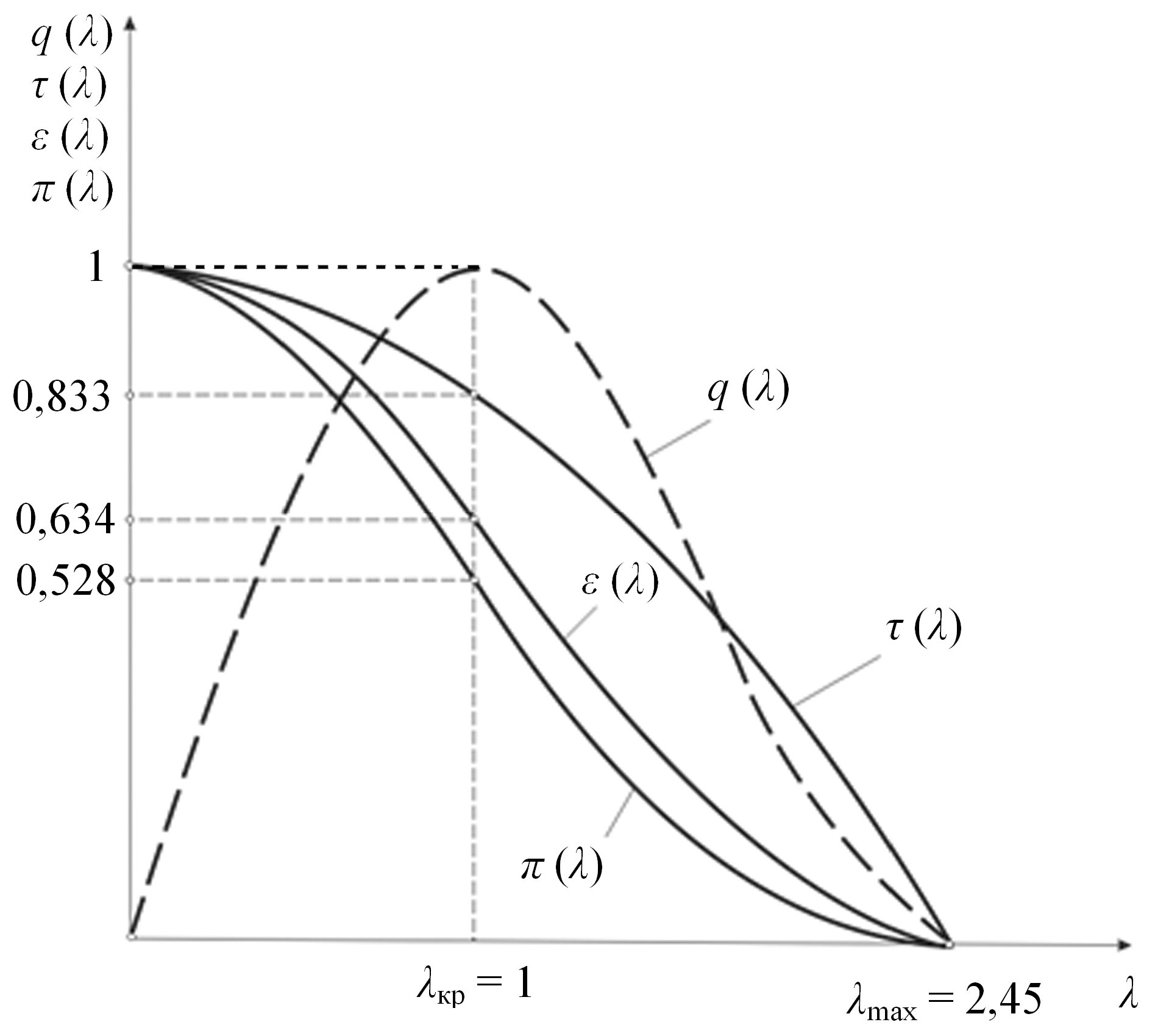
Рис. 8.11. Графическое изображение газодинамических функций

Таблицы газодинамических функций, заранее рассчитанные и приведённые в виде таблиц, существенно упрощают анализ и расчёт газовых потоков.

Здесь рассмотрены пять наиболее употребительных газодинамических функций. В расчётах иногда используют и другие величины, описание и таблицы которых приведены в приложении П.4.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Газодинамические функции – это математические выражения, показывающие характеристики одномерного потока газов (связь между параметрами состояния), характеристики плотности потока, импульса силы и количества движения потока при изменении располагаемого перепада давлений на входе и выходе из рассматриваемого канала.

Для расчета применяют относительные скорости движения:

- скорости звука, т.е. скорости распространения сигнала в упругой среде газов;

- критической скорости – условной скорости потока.

Скорость звука является однозначной зависимостью от местной статической температуры в потоке газа; критическая скорость однозначно зависит от температуры адиабатного торможения потока во входном сечении канала, если полагают, что эта величина в дальнейшем остается неизменной при изменении разности давлений на входе и выходе.

При изменении перепада давлений в рассматриваемом канале происходит увеличение скорости движения потока. При неизменной площади сечения на выходе имеет место кризис течения – скорость движения потока при каком-то значении отношения давлений достигает скорости звука, и при дальнейшем увеличении перепада давлений не может возрасти. Этому моменту соответствует равенство единице как отношения скорости потока к скорости звука, так и отношения скорости потока к критической скорости.

Отношение скорости потока к местной скорости звука называется числом Маха и записывается , где

Т –температура газа, К

- показатель адиабаты, отношение теплоемкостей при постоянном давлении и объеме.

R – газовая постоянная, Дж/кг град

Число М может иметь любые значения от 0 и до бесконечности.

Отношение скорости потока к критической скорости записывается:

Т * - температура торможения, К

Число λ может достигать значения от 0 до

Естественно, удобнее зависимости параметров потока определять по значению λ, а число Маха связано с ним зависимостью:

Функции τ(λ), Π(λ) и ε(λ), характеризующие термодинамическое состояние газа

Функции q(λ) и y(λ) , характеризующие поток массы

Функции z(λ), f(λ) и r(λ), характеризующие поток импульса

Одним из определяющих факторов является показатель адиабаты k. В соответствии с молекулярно-кинетической теорией газов имеется следующая модель. Значение теплоемкостей с_р и с_v зависят от газовой постоянной и числа степеней свободы i движения атомов в молекуле. Для одноатомных молекул число степеней свободы равно 3, для двух-атомных или 5 или 8. Тогда , а и k будет иметь значения 1,66 1,4 и 1,25. Для смеси газов возможный диапазон значений k колеблется между 1,66 и 1,20.

1. Приведенная адиабатная скорость – это отношение скорости газа при адиабатном течении к критической скорости.

, м (1)

где к – показатель адиабаты,

Тт – температура торможения,

Рт – давление торможения,

- удельный объем в заторможенном состоянии, м 3 /кг.

изменяется от =0 – неподвижный поток до _мах= - абсолютный вакуум.

Для двухатомных газов к=1,4, для них же _мах=2,45, для перегретого пара к=1,3, _мах=2,77, для сухого насыщенного пара к=1,13, _мах=4,05.

2. - относительная температура

(2)

3. П₍ ₎ - относительное давление – отношение статического давление движущегося газа к давлению торможения (Р_т)_.

П = (3)

4. - относительная плотность:

(5)

5. q - относительная массовая скорость – это отношение массовой скорости движущегося потока в данном сечении к массовой скорости этого потока в критическом сечении.

q= q=

где f_k – критическое сечение потока, f – сечение потока.

Принципиальная схема струйного компрессора

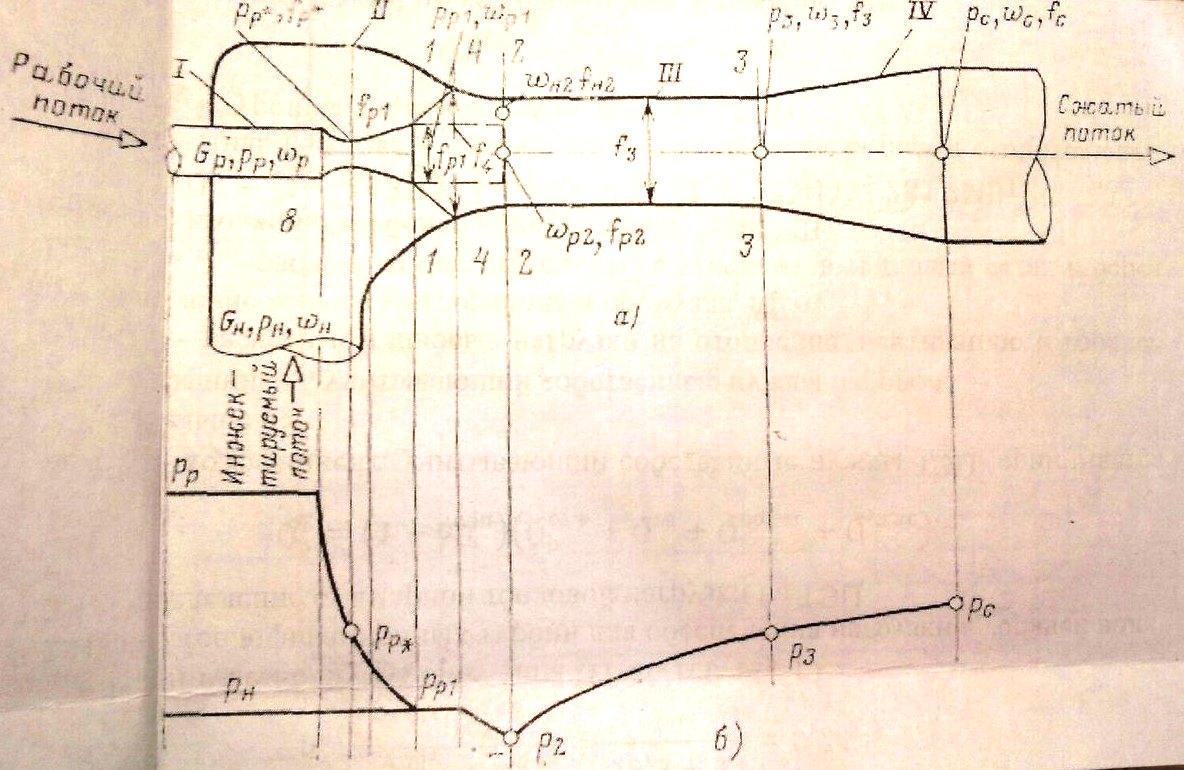
Рабочий газ с давлением Р_р и скоростью _р подводится к рабочему соплу, которое имеет расширяющуюся форму, поскольку степень снижения давления газа в сопле Р_н/Р_р < П. В результате расширения, давление газа падает с Р_р до Р_р1 = Р_н, а скорость увеличивается с w_p до w_p_1.

Рабочий газ, выходящий из сопла в приемную камеру со скоростью w_р1,подсасывает из приемной камеры газ, который подводится в нее с давлением Р_н. По мере удаления от сопла массовый расход потока увеличивается за счёт инжектируемой среды, а поперечное сечение движущегося потока растет. На некотором расстоянии от выходного сечения сопла поток, движущийся по направлению к камере смешения, заполняет всё сечение f₄ приёмной камеры. Сечение f₄ является конечным сечением приемной камеры и начальным сечением камеры смешения. В выходном сечении 2-2 давление потока равно Р₂.

Выравнивание скоростей в этой камере сопровождается увеличением давления от Р₂ до Р₃, далее поток поступает в диффузор, где давление растет с Р₃ до Р_с, а скорость падает с w₃ до w_c. При Р_с и w_c смешанный поток выходит из струйного аппарата.

где i_p_,i_н,i_c – энтальпии рабочей инжектируемой и сжатой среды.

Из эксегетического баланса можно записать :

G_pe_p+G_не_н=(G_p-G_н)е_с+ , где - потери эксергии в аппарате.

Для идеальных условий работы U:

Принципиальная схема пароэжекторных холодильных установок

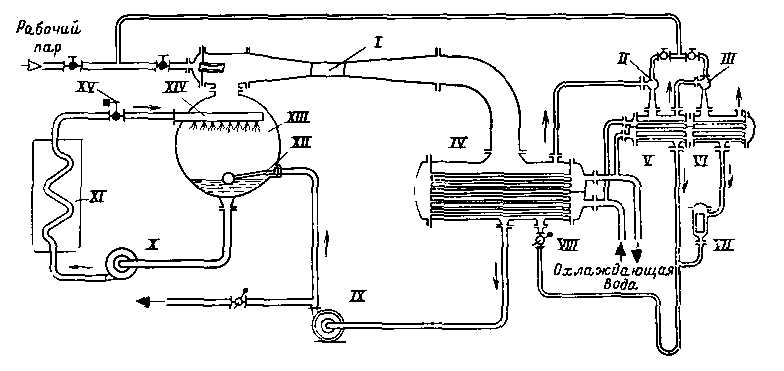
I – главный эжектор;

II, III – вспомогательный эжектор верхней и нижней ступени;

IV – главный конденсатор;

V – вспомогательный конденсатор нижней ступени;

VI – вспомогательный конденсатор верхней ступени;

VII – поплавковый вентиль;

VIII;XII – дроссельные вентили;

IX – конденсатный насос;

X – холодноводный насос;

XI – потребитель холода;

XIV – распределительная гребенка;

XV – регулирующий вентиль;

Эти установки работают по заданной схеме. Благодаря простоте применяются в схемах кондиционирования воздуха.

Основным аппаратом этих установок, соответствующем по назначению компрессору, служит струйный эжектор.

Подлежащая охлаждению вода из камер кондиционирования воздуха или из охлаждающих рубашек технологических аппаратов поступает через дроссельный вентиль XVI и распределительную гребенку XIV в испаритель XIII холодильной установки.

С помощью главного эжектора I установки в испарителе поддерживается давление Р_н=Р₀, соответствующие температуре испарения (кипения) t₀ охлажденной воды. Так как вода, поступающая на охлаждение, имеет температуру t_в> t₀, то она в испарителе вскипает, а температура ее снижается с t_в до t_0. Охлажденная вода с температурой t₀ забирается холодноводным насосом и подается к потребителям. Водяной пар, выделившийся в испарителе из охлаждаемой воды, отсасывается главным эжектором. При установившемся режиме:

G_в – расход воды, поступающей на охлаждение от потребителей в холодильную установку;

G_s – расход охлаждаемой воды, подаваемой от холодильной установки к потребителям.

Аналогично расход пара, отводимого от испарителя равен расходу конденсатора, подаваемого из главного конденсатора в испаритель.

3) тепловой баланс испарителя

G_s и G_н – расход воды и пара из испарителя;

i_в и i_k – энтальпии воды, поступающей в испаритель из системы кондиционирования и из конденсатора установки;

i_o – энтальпия холодной воды после испарителя;

i_н – энтальпия пара после испарителя.

4) отношение массовых расходов пара и воды, выводимых из испарителя

G_н/G_s=(i_B-i₀)/(i_н-i_k)

5) отношение расхода пара на главный эжектор к расходу охлажденной воды

Gp/Gs= /u=1/u*

6) удельный расход тепла на выработку холода

Э_х=

I_p – энтальпия рабочего пара перед главным эжектором при близких значениях i_p и i_н можно принять Э_х=1/U.

7) холодильный коэффициент

1/Э_х=u(i_n-i_k)/(i_p-i_k)

8) удельный расход эксергии рабочего пара на выработку холода

Е_х=

9) КПД установки

Е_хол/E_раб=u(i_n-i_k) /( )

- коэффициент работоспособности

=1-Т_ос/T_o

Т₀ – температура воды после испарителя

Принципиальная схема вихревой трубы

Вихревая труба – аппарат без движущихся частей. Сжатый газ при давлении Р_с и температуре Т_с обычно равной или близкой к Т_ос вводится внутрь цилиндрической трубы I через сопло II тангенциально, т.е. по касательной к внутренней поверхности трубы. Поступивший поток газа, совершающий вращательное движение по отношению к ее оси, перемещается по периферии трубы от соплового сечения С – С к так называемому горячему торцу трубы Г – Г. Через кольцевую щель IV в выходном торце Г – Г трубы часть периферийного потока газа выводится из нее при температуре торможения Т_г>Т_с. Остальной газовый поток проходит по центральной части трубы противотоком к периферийному потоку газа и выводится из нее через диафрагму III и холодный торец трубы Х – Х с температурой торможения Т_хс. Давления обоих потоков газа на выходе из трубы ниже давления Р_с, т.е. Р_хс и Р_гс. Работа вихревой трубы может проходить при двух принципиально различных режимах течения холодного потока в диафрагме: докритическом и критическом.

При докритическом режиме, когда осевая скорость потока в диафрагме меньше критической давление в отверстии диафрагмы равно давлению на холодном конце трубы после диафрагмы P_д=Р_х. На этом режиме труба работает при относительно малых массовых расходах холодного потока. При увеличении расхода холодного потока осевая скорость в диафрагме возрастает. При некотором расходе холодного потока эта скорость достигает критической скорости холодного потока .

Этот режим является переходным от докритического к критическому. При дальнейшем увеличении массового расхода холодного потока труба переходит на критический режим. При работе на критическом режиме осевая скорость холодного потока в диафрагме равно критической , а P_д>Р_х.

Для конечного участка потока 1-2 уравнение энергии имеет вид:

где h* - полная энтальпия, или энтальпия адиабатного торможения при скорости потока W=0. Таким образом, при движении газа его полная энергия, состоящая из кинетической энергии видимого движения и энергии, выражаемой энтальпией h=u+pv, остается постоянной. Всякое изменение кинетической энергии вызывает соответствующее изменение его энтальпии, а, следовательно, и температуры. В соплах скорость увеличивается, а температура уменьшается. В диффузорах скорость уменьшается, а температура увеличивается.

При полном торможении потока (w=0) температура принимает наибольшее значение и называется температурой полного торможения Т*. Для идеального газа с_р=const, h=c_pT и h*=c_pT*. Тогда из уравнения (1) следует, что:

где Т – статическая температура (температура движущейся среды). В уравнении (2) второй член правой части преобразуем к следующему виду:

где R=c_p-c_v по уравнению Майера; c_p=кc_v, M=W/a – число Маха; a 2 =кRT;
а – скорость звука. Тогда окончательно получим выражение для расчета скорости торможения:

Расчет давления торможения проводится по формуле:

Плотность заторможенного потока будет равна:

Для расчета параметров можно использовать таблицы газодинамических функций, которые облегчают решение задач. При этом вводится приведенная скорость , где критическая скорость , а . Тогда получим:

и газодинамическая функция .

Располагая таблицами, в которых для каждого значения или М указаны значения функций , можно быстро переходить от действительных (термодинамических) параметров потока к параметрам торможения и обратно. Выбор для расчета чисел М или определяется удобствами применения в каждом конкретном случае. Для определения расхода газа через произвольный канал по известной площади проходного сечения f, числу М или и по параметрам заторможенного потока можно воспользоваться газодинамической функцией , которая возрастает с ростом числа М при Мq_max=1 при М= =1 и снова убывает при M>1.

Тогда уравнение расхода можно записать в виде , где и , где , т.е. . Для воздуха к=1,4, R=297 Дж/кгК, m=0.3965.

Например, при определении изменения параметров потока газа по длине сопла, принимая р₁=р* и Т₁=Т* при заданном значении показателя адиабаты к и известных геометрических размерах сопла и расхода G можно определить изменение массовой скорости по длине сопла, величину а_кр _кр и функцию q. Далее по таблицам при заданном к можно определить функции и величины и .

В теории турбомашин не удобно пользоваться физической скоростью. Это связано с тем, что на практике важнее знать не саму величину скорости, а то как она соотносится со скоростью звука. Дело в том, что вблизи скорости звука в потоке появляются дополнительные волновые потери, связанные со скачками уплотнения, что мешает получению высоких КПД и требует иных подходов к проектированию.

Скорость звука представляет собой скорость распространения слабых возмущений от источника звука в среде. Как известно она зависит от температуры среды:

где - показатель изоэнтропы

R– газовая постоянная,.

Для воздуха при скорость звука равна. Поэтому, например скорость потокана входе в компрессор, где температура воздуха равна атмосферной, является сверхзвуковой. В то тремя как на выходе из компрессора, когда рабочее нагрелось в результате сжатия те же400м/сявляются глубоким дозвуком.

Оценить насколько далеко скорость рабочего тела отстоит от скорости звука можно с помощью безразмерных скоростей: числа Маха и приведенной скоростью .

Число Махапредставляет собой отношение скорости газа к местной скорости звука

где Т– статическая температура газа, К.

Число Маха может принимать любые положительные значения.

Под приведенной скоростью понимается отношение скорости газа к критической скорости

где - температура торможения, К.

Под критической скоростьюпонимают такую скорость течения газа, которая равна местной скорости звука. Чтобы представить ее следует рассмотреть процесс истечения газа из резервуара через сопло в атмосферу. Это течение является энергоизолированным. По мере нарастания скорости по длине сопла, температура а, следовательно, скорость звука уменьшаются. Таким образом в различных сечениях одного и того же потока скорость звука получается различной. В начале сопла меньше скорости потока, в конце – превышает ее. Где-то в средней части сопла существует сечение, в котором скорость потока равна местной скорости звука. Это сечение называетсякритическим, а параметры потока в нем критическими параметрами.

Приведенная скорость может изменяться в диапазоне от 0до.

Приведенная скорость и число МахаМсвязаны между собой следующими соотношениями

Числа Миявляются критериями подобия для сжимаемой жидкости. Так, например если в двух геометрически подобных каналах числаМна входе будут одинаковы, то отношения скоростей, давлений, плотностей и температур в двух сечениях одного канала будут равны отношению параметров в сходных сечениях подобного канала.

2.1.3 Газодинамические функции

Газодинамические функции представляют собой безразмерные функции приведенной скорости или числа МахаМ, равные отношениям важнейших параметров, характеризующих одномерный поток в различных его сечениях, к значениям этих параметров в критических сечениях или к значениям параметров заторможенного потока. Использование газодинамических функций совместно с параметрами заторможенного потока представляет значительное удобство при инженерных расчетах потоков.

Наиболее часто используются следующие газодинамические функции

- функция “тау от лямбда” , равная отношению статической температуры потокаТк температуре заторможенного потокаТ * в том же сечении

- функция “пи от лямбда” ,равная отношению статического давления потокаpк давлению заторможенного потокаp * в том же сечении

- функция “эпсилон от лямбда” ,равная отношению статической плотности потока к плотности заторможенного потокав том же сечении

- функция “q от лямбда” - приведенная плотность тока, равная отношению плотности тока в произвольном сечении к плотности тока в критическом сечении

Они заранее рассчитываются для всех значений приведенной скорости и сводятся в таблицы газодинамических функций. Последние составляются для различных показателей адиабаты. Наиболее распространены таблицы для воздухаk=1,4и для продуктов сгорания керосинаk=1,33(Приложение А).

Зная значение одной из функций с помощью таблиц легко найти значения остальных. По этой причине таблицы ГДФ получили широкое распространение в отечественной практике термогазодинамичеких расчетов в различных отраслях.

Читайте также: