Как удалить лямбда переходы
Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.
Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…
λ-исчисление: основные понятия
Синтаксис
В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.
Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.
Термы:
| переменная: | x |
| лямбда-абстракция (анонимная функция): | λx.t , где x — аргумент функции, t — её тело. |
| применение функции (аппликация): | f x , где f — функция, x — подставляемое в неё значение аргумента |
- Применение функции левоассоциативно. Т.е. s t u — это тоже самое, что (s t) u
- Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е. λx. λy. x y x означает то же самое, что λx. (λy. ((x y) x))
- Скобки явно указывают группировку действий.
Процесс вычисления
Рассмотрим следующий терм-применение:
Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:
который для простоты можно переписать как
(напомним, что id — это функция тождества вида λx.x )
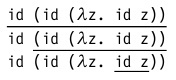
В этом терме содержится три редекса:
Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение
(λx.λy. x) z ((λx.x x)(λx.x x))
Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y . Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y , а z — первоначальный терм имел бы вид (λx.λz.x)y и после редукции выглядел бы как λz.y . Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.
Так же бывает, что у нас есть абстракция λx.t x , причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t . Такое преобразование называется η-конверсией.
На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.
Это до предела упрощенная модель компьютера имеющая конечное число состояний, которая жертвует всеми особенностями компьютеров такие как ОЗУ, постоянная память, устройства ввода-вывода и процессорными ядрами в обмен на простоту понимания, удобство рассуждения и легкость программной или аппаратной реализации.
С помощью КА можно реализовать такие вещи как, регулярные выражения, лексический анализатор, ИИ в играх и тд.
У конечных автоматов имеется таблица переходов, текущее состояние автомата, стартовое состояние и заключительное состояние.
Таблица переходов — В ней хранятся переходы для текущего состояния и входного символа. Простейшая реализация может быть как двумерный массив.
Здесь видно, что из состояния 0 в состояние 1 можно попасть только, если у нас будет входной символ 'a', из состояния 1 в состояние 2, если символ 'b'.
Текущее состояние — множество состояний в котором автомат может находиться в данный момент времени.
Стартовое состояние — состояние откуда КА начинает свою работу.
Заключительное состояние — множество состояний в которых автомат принимает определенную цепочку символов, в ином случае отвергает.
Детерминированные конечные автоматы (deterministic finite automaton)
Простейший КА, в котором может быть одно состояние в текущий момент времени, обладает детерминированностью.
Детерминированность — для всех состояний имеется максимум и минимум одно правило для любого возможного входного символа, то есть например, для состояния 1 не может быть два перехода с одним и тем же входным символом.

Здесь изображена диаграмма переходов для ДКА, визуализация примера 1. Состояние 3 является заключающим. По диаграмме видно, что ДКА принимает цепочку символов только в том случае, если будет последовательность из символов 'a', 'b' и 'c'.
Недетерминированные конечные автоматы (nondeterministic finite automaton)
НКА не является каким-то существенным улучшением ДКА, просто в нем добавлен так сказать синтаксический сахар, в виде свободных переходов, недетерминированности и множеств состояний. Реализовать можно как массив состоящий из структур в которой хранится состояние, входной символ и следующее состояние.
Свободные переходы (эпсилон переходы) — переходы, которые можно совершать без чтения входного символа.
Недетерминированность — ноль и более переходов для одного символа в каких-либо состояниях.
Множества состояний — в один момент времени НКА может находится в нескольких состояниях.
Заключительное состояние обозначается двойным кругом.

В стартовом состоянии у нас текущим состоянием является , при входном символе 'b' у нас появляется возможность, пойти в состояние 1 и в состояние 2, то есть после входного символа 'b' текущим состоянием является множество .
Свободным переходом обозначается пунктирной линией.

Здесь видно два свободных перехода из стартового состояния, то есть без чтения входного символа мы сразу находимся в множестве состоянии .
Для преобразования НКА в ДКА используется алгоритм Томпсона.
При преобразовании НКА в ДКА может получиться не совсем минимальный ДКА и для его минимизации можно применить алгоритм Бржозовского.
Это тот же КА, но с дополнительной памятью в виде стека. Теперь для совершения перехода нужно учитывать еще несколько факторов, символ который нужно удалить из стека и символы которые нужно добавить в стек.
КАМП можно применять в таких местах, где может быть неограниченное количество вложений, например при разборе языков программирование или подсчету вложенных скобок в математических выражениях. Реализовать с помощью КА невозможно, ведь количество возможных состояний конечно в отличие от стека (я понимаю, что память тоже конечна).
Удаление символа из стека — при любом переходе решается какой символ вытолкнуть, если на вершине стека не оказалось такого символа, то он и не выталкивается. Так же если символ нужно оставить в стеке, то он добавляется вместе с добавляемыми символами.
Добавление символов в стек — при любом переходе решает какие символы добавить в стек.
- Детерминированные — к нему применяются те же правила как к ДКА к тому же завершает работу только в заключительном состоянии.
- Недетерминированные — к нему применяются те же правила как к НКА к тому же он может завершать работу в заключительном состоянии или когда стек станет пуст.
Шаблон: входной_символ; удаляемый_символ/добавляемый символ. На дно стека добавляется символ $ для, того, что понять когда он закончился.

Этот КАМП подсчитывает вложенность скобок, за счет добавления и удаления символов из стека.
ДАМП не равен НАМП, поэтому невозможно одно преобразовать в другое, следовательно НАМП обладает преимуществом перед ДАМП.
Самая мощная машина из существующих, его преимущество перед другими в ленте с которой он может работать как хочет. В нем нет свободных переходов. Умеет интерпретировать другие автоматы такие как КА, КАМП.
Лента — это одномерный массив в который могут записываться данные за счет головки над ячейкой, который можно заранее заполнить входными данными.
Шаблон: считаный_символ_с_головки/записаный_символ; сторона_смещения_головки. края ленты обозначаются '_'.

Эта МТ выполняет инкремент двоичного числа, головка стоит слева, там где начинается лента.
- Если находится в состоянии 1 и прочитан нуль, записать единицу, сдвинуть вправо и перейти в состояние 2.
- Если находится в состоянии 1 и прочитана единица, записать нуль, сдвинуть влево и перейти в состояние 1.
- Еcли находится в состоянии 1 и прочитан пустой квадратик, записать единицу, сдвинуть вправо и перейти в состояние 2.
- Если находится в состоянии 2 и прочитан нуль, записать нуль, сдвинуть вправо и остаться в состояние 2.
- Если находится в состоянии 2 и прочитана единица, записать единицу, сдвинуть вправо и остаться в состояние 2.
- Если находится в состоянии 2 и прочитать пустой квадратик, записать пустой квадратик, сдвинуть влево и перейти в состояние 3.
ДМТ эквивалентен НМТ, так, что они тоже не различаются.
Универсальная машина Тьюринга (universal Turing machine)
Машина которая может порождать другие машины Тьюринга, получая на входную ленту данные машины.
Mon, May. 22nd, 2006, 12:25 am
Седьмой семинар
Тема: Регулярные языки и конечные автоматы (продолжение).
Для получения регулярного языка, допускаемого конечным автоматом, в общем случае необходимо решить систему уравнений в полукольце языков (аналогично решалась задача поиска кратчайших расстояний в графе): . Не трудно убедиться, что это идемпотентное полукольцо с итерацией, в котором мы можем решать уравнение вида (см. выше). Чтобы получить систему уравнений, необходимо построить матрицу переходов для графа конечного автомата.
Рассмотрим пример, в котором регулярный язык без составления конечного автомата и системы уравнений достаточно сложно. Рассмотрим алфавит , необходимо получить регулярное выражения для языка, содержащего только чётное число единиц и чётное число нулей. Попытки придумать регулярное выражение ``в лоб'' (например, ) дадут только частные случаи. Построим конечный автомат, допускающий цепочки такого языка: очевидно, что возможно только четыре состояния: ``чётное число нулей и единиц'', ``чётное число нулей, нечётное -- единиц'', ``нечётное число нулей и единиц'' и ``нечётное число нулей и чётное число единиц'', автомат со всеми возможными переходами показан на рисунке 0.
Каждому состоянию конечного автомата ставится в соответствие переменная . Значение этой переменной суть есть регулярное выражение, задающее все слова, которые допускаются кончным автоматом, старующем из данного состояния. Очевидно, что язык, допускаемый конечным автоматом получается сложением переменных всех стартовых состояний.
Каждой строке матрицы соответствует одно уравнение, при этом всем уравнениям, соответствующим конечным состояниям автомата, необходимо прибавить .
В нашем примере получается следующая система уравнений, которая имеет решение:
Таким образом, регулярное выражение для языка, допускаемого автоматом, равно:
Детерминизация конечных автоматов
Выше уже было сказано о том, что при работе конечного автомата возможны ``конфликтные ситуации'', когда существует два правила с одинаковой левой частью или -переходы -- в этом случае необходимо ``знать заранее'', какой путь следует выбрать, чтобы цепочка всё же была прочитана. Такой подход очень неудобен в реализации, поэтому воникает задача детерминизации конечного автомата, т.е. приведение его к такому виду, что ``конфликтныйе ситуации не возможны'', а язык, допускаемый автоматом, не изменяется.
Существует формальный алгоритм детерминизации автомата, который состоит из двух шагов:
- удаление -переходов;
- собственно детерминизация.
Для данного автомата , автомат без -переходов будет иметь вид:
где множество вершин , т.е. начальная вершина плюс все вершины, в которые входит хотя бы одна не--дуга; множество конечных вершин , т.е. множество оставшихся конечных вершин плюс все вершины, достижимые из конечных по -путям (одна или набор -дуг); множество правил перехода -- оставлятются только не--переходы, к ним добавляются переходы, следующими за -путями из данной вершины (т.е. для в добавляется правило ).
Рассмотрим пример: на рисунке 1 показаны автоматы с -переходами и без -- при этом они допускают один и тот же язык.
Детерминизация производится построением новых вершин и переходов. При этом в качестве вершин графа автомата могут теперь выступать не отдельные состояния изначального автомата, анаборы состояний, например .
В качестве нового исходного состояния принимается состояние . Далее для всех букв алфавита стоятся новые вершины, в которые можно попасть из данной вершины. Для нашего примера все новые состояния и переходы будут выглядеть так:
Новыми конечными вершинами являются все вершины, содержащие в себе хоть одну из конечных вершин исходного автомата: , , , .
Новые вершины можно переименовать. Граф детерменизированного автомата показан на рисунке 2.
Существует теорема, согласно которой для каждого автомата может быть построен эквивалентный (допускающий тот же язык) автомат. Это позволяет для любого регулярного языка построить детерминизированный автомат.
Из этой теоремы есть интересное следствие -- с помощью детерменизированного автомата можно получать автоматы не досускающие заданную цепочку. Для этого необходимо в детерминизированном автомате, допускающем данную цепочку, взять в качестве конечных вершин дополнение относительно всех вершин: .
Рассмотрим пример -- необходимо получить автомат (в алфавите ), не допускающий идущих подряд букв . На рисунке 3 показан исходный автомат, допускающий все слова, содержащие подряд , затем тот же автомат, но детерминизированный. Третьим показан автомат, не досускающий цепочки, содержащие подряд . В данном случае две правые вершины в последнем автомате можно объединить как неверные состояния, в том смысле, что попав туда, автомат заведомо не прочитает заданную цепочку.
Делегаты
Делегат это особый тип. И объявляется он по особому:
Тут все просто, есть ключевое слово delegate, а дальше сам делегат с именем MyDelegate, возвращаемым типом int и одним аргументом типа string.
По факту же при компиляции кода в CIL — компилятор превращает каждый такой тип-делегат в одноименный тип-класс и все экземпляры данного типа-делегата по факту являются экземплярами соответствующих типов-классов. Каждый такой класс наследует тип MulticastDelegate от которого ему достаются методы Combine и Remove, содержит конструктор с двумя аргументами target (Object) и methodPtr (IntPtr), поле invocationList (Object), и три собственных метода Invoke, BeginInvoke, EndEnvoke.
Объявляя новый тип-делегат мы сразу через синтаксис его объявления жестко определяем сигнатуру допустимых методов, которыми могут быть инициализированы экземпляры такого делегата. Это сразу влияет на сигнатуру автогенерируемых методов Invoke, BeginInvoke, EndEnvoke, поэтому эти методы и не наследуются от базового типа а определяются для каждого типа-делегата отдельно.
Экземпляр же такого делегата стоит понимать как ссылку на конкретный метод или список методов, который куда то будет передан и скорее всего выполнен уже на той стороне. Причем клиент не сможет передать с методом значение аргументов с которыми он будет выполнен (если только мы этого ему не позволим), или поменять его сигнатуру. Но он сможет определить логику работы метода, то есть его тело.
Это удобно и безопасно для нашего кода так как мы знаем какой тип аргумента передать в делегат при выполнении и какой возвращаемый тип ожидать от делегата.
Если пофантазировать, то можно предоставить право передачи аргумента для делегатов клиентской стороне, например создать метод с аргументом делегатом и аргументом который внутри нашего метода этому делегату будет передан, что позволит клиенту задавать еще и значение аргумента для метода в делегате. Например таким образом.
Создавая в коде экземпляр делегата его конструктору передается метод (подойдет и экземплярный и статический, главное чтобы сигнатура метода совпадала с сигнатурой делегата). Если метод экземплярный то в поле target записывается ссылка на экземпляр-владелец метода (он нужен нам, ведь если метод экземплярный то это как минимум подразумевает работу с полями этого объекта target), а в methodPtr ссылка на метод. Если метод статический то записываются в поля target и methodPtr будут записаны null и ссылка на метод соответственно.
Инициализировать переменную делегата можно через создание экземпляра делегата:
Или упрощенный синтаксис без вызова конструктора:
Организовать передачу/получение экземпляра делегата можно по разному. Так как делегат это в итоге всего лишь тип-класс, то можно свободно создавать поля, свойства, аргументы методов и т.д. конкретного типа делегата.
Invoke — синхронное выполнение метода который храниться в делегате.
BeginInvoke, EndEnvoke — аналогично но асинхронное.
Вызывать выполнение методов хранящихся в делегате можно и через упрощенный синтаксис:
это аналогично записи:
А зачем делегату поле invocationList?
Поле invocationList имеет значение null для экземпляра делегата пока делегат хранит ссылку на один метод. Этот метод можно всегда перезаписать на другой приравняв через " членом типа в котором вы используете данное лямбда выражение, и передается в конструктор делегата явно в CIL коде.
Причем компилятор анализирует содержит ли выражение в своем теле операции с экземплярными полями типа в котором выражение обновлено или нет. Если да то генерируемый метод будет экземплярным, а если нет, то метод будет статическим. Использование в лямбда выражении статических полей данного типа, а так же экземпляров и экземплярных полей других типов на это не влияют.
Вы можете спросить почему бы CLR не генерировать экземплярный метод в обоих случаях, ответ прост — такому методу нужен дополнительный параметр this, что делает его выполнение более трудоемким по сравнению со статическим.
Помимо этого CLR создает конструкцию, которая кэширует делегат с нашим методом в анонимном закрытом поле (все там же в нашем типе где было использовано лямбда выражении) при первом обращении к нему, а при последующих просто читает из его из поля. И действительно, нет никакого толка создавать его заново каждый раз, ведь информация о методе заданном выражением неизменна на этапе выполнения программы.
В итоге
В этом дополнении мы подробно докажем корректность приведенного в доказательстве теоремы 7.7 о детерминизации алгоритма построения по заданному конечному автомату эквивалентного ему детерминированного конечного автомата.
Сначала докажем корректность алгоритма удаления λ-переходов, после чего подобное доказательство проведем уже для самого алгоритма детерминизации.
1. Корректность алгоритма удаления λ-переходов
Пусть — исходный конечный автомат, а — конечный автомат без λ-переходов, построенный согласно алгоритму, описанному в доказательстве теоремы 7.7 о детерминизации. Мы должны доказать, что .
а. Докажем, что для любых цепочки из того, что в конечном автомате цепочка в , т.е. имеет место , следует, что в конечном автомате в такое состояние , что в имеет место , т.е. либо , либо в существует путь ненулевой длины по пустым дугам из в : (на рис. 7.32 и на аналогичных следующих рисунках мы соединяем тонкой штриховой линией кружки, изображающие одно и то же состояние, которое остается после удаления λ-переходов).
Возможны два случая для состояния : оно или остается после удаления λ-переходов, т.е. , либо удаляется в результате удаления λ-переходов, т.е. .
1°. Состояние остается после удаления λ-переходов, т.е. .
Проведем индукцию по длине пути в конечном автомате , на котором читается цепочка доказываемое свойство имеет место, и пусть цепочка на некотором пути длины из в , то есть . Тогда существует такое состояние , что в имеет место
Если , то , и тогда цепочка на некотором пути длины .
При остается только использовать индукционное предположение, и тогда найдется такое состояние , что в и в имеется , но так как в имеется , то в выполняется (рис. 7.33). Таким образом, мы, исходя из условия, что в имеется , нашли такое состояние , что в , а при этом в выполняется , что и требовалось доказать.
Пусть теперь , т.е. состояние г удаляется при удалении λ-переходов. Это значит, что в состояние заходят только дуги с меткой в в конечном автомате читается цепочка , то найдется такое состояние , что в будет иметь место , и и тогда )- Согласно предположению индукции, отсюда следует, что в , где в , а так как в имеет место , то в имеется (рис. 7.34), и мы снова, исходя из условия, что в имеется , нашли в такое состояние , что цепочка , при том что в исходном конечном автомате из этого состояния ведет путь по пустым дугам в состояние .
Итак, случай в (7.9) проанализирован полностью.
Пусть . Если при этом , то, согласно предположению индукции, существует такое состояние , что в конечном автомате , при том что в имеется .
При конечного автомата , метка которой содержит символ а, останется и в конечном автомате , то есть в .
При , т.е. в случае, когда в конечном автомате заключаем, что в существует тройка состояний , такая, что и . По построению конечного автомата в , то есть (рис. 7.35). Случай тем самым полностью проанализирован.
Если же , т.е. состояние удаляется при переходе к конечному автомату , что в цепочка читается на некотором пути длины в , а из в ведет путь ненулевой длины по пустым дугам, т.е. в конечном автомате имеется (рис. 7.36). Тогда, согласно предположению индукции, в , где в . Тогда опять в возникает тройка состояний , такая, что и (см. рис. 7.36). По построению конечного автомата . Итак, в , т.е. в конечном автомате в .
2°. Состояние удаляется при удалении λ-переходов, то есть .
В этом случае для некоторого будет выполняться в конечном автомате , откуда, согласно результатам, доказанным для случая 1°, в конечном автомате , такого, что в имеется . Следовательно, в , то есть , что и требовалось доказать.
Итак, мы полностью доказали, что любая цепочка на некотором пути из начального состояния в какое-то состояние , читается также и в автомате в такое состояние , что в имеет место .
б. Докажем, что для любых состояния и цепочки в какое-то состояние , т.е. имеет место , следует, что в исходном конечном автомате цепочка в в .
Проведем опять индукцию по длине пути в конечном автомате , допустим, что в . Тогда для некоторого в , причем , а так как в нет λ-переходов, то , то есть имеется . Далее, из того, что в в , на которой читается символ в , и тогда в , либо в существует такое состояние , что . Как в том, так и в другом случае имеем в конечном автомате , т.е. в цепочка .
в. Пусть цепочка , т.е. для некоторого заключительного состояния цепочка . Тогда из п. а следует, что в в такое состояние , что в . Если , то ; если же , т.е. в существует путь ненулевой длины по пустым дугам из в , то, согласно определению множества . Итак, .
Обратно, если , т.е. в , где , то, согласно п. б, и в . Но так как в множество , либо те его вершины, из которых заключительная вершина достижима по пустым дугам, то найдется такое , что в имеем и , то есть в конечном автомате , откуда .
Итак, что и обосновывает корректность алгоритма удаления λ-переходов.
2. Корректность алгоритма детерминизации
Пусть теперь — исходный конечный автомат без λ-переходов, а — детерминированный конечный автомат, построенный согласно алгоритму, описанному в доказательстве теоремы о детерминизации, т.е.
и для любого и любого имеем . Мы должны доказать, что .
а. Докажем, что для любых цепочки из того, что в цепочка в какое-то состояние , то есть , следует, что эта цепочка читается и в в состояние-множество , которое содержит , т.е. в имеется , где .
Доказательство проводим индукцией по длине пути в конечном автомате , на котором читается цепочка , допустим, что цепочка на некотором пути длины из в , то есть . Тогда найдется такое , что (где и )
Тогда, согласно предположению индукции, в конечном автомате в такое . Так как конечный автомат и метка этой дуги содержит символ в . Состояние есть объединение всех множеств при . В частности, при множество состояний в силу (7.10) содержит состояние . Следовательно, это состояние принадлежит и множеству , и тогда в , то есть .
б. Докажем теперь, что для любой цепочки из в в .
Проведем индукцию по длине цепочки , т.е. для пустой цепочки , и пусть в , то есть , в , причем и . Тогда, согласно предположению индукции, в имеется для каждого , то любой элемент в есть элемент некоторого множества при есть дуга . Но, как мы только что доказали, для любого состояния , т.е. для любого имеем в конечном автомате , откуда , что и требовалось доказать.
в. Теперь, если , т.е. цепочка на некотором пути из начального состояния в одно из заключительных, а именно для некоторого , то, согласно результатам, доказанным в п. а, в , содержащее вершину , то есть и .
Обратно, если , то есть в будем иметь в конечном автомате имеем . Но состояние-множество обязательно содержит некоторое заключительное состояние исходного конечного автомата (состояние из подмножества получим в , что и означает .
Итак, и тем самым вся процедура детерминизации конечных автоматов полностью обоснована.
Читайте также:

