Добротность формула что такое лямбда
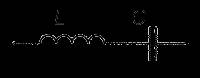
LC - фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли. Это антиквариат, причём наиболее древним из семейства фильтров, построенных при помощи индуктивностей и ёмкостей, является параллельный LC колебательный контур, изображённый на Рис.1.
Частотная зависимость коэффициента передачи такого LC контура соответствует характеристике резонансного полосового фильтра. Именно с этого самого простого LC-фильтра мы и начнём расчёт.
Как уже было сказано - LC контур, включённый по схеме, приведённой на Рис.1, представляет собой узкополосный полосовой резонансный фильтр, настроенный на частоту:
fо= 1/(2π√ LС ) .
На резонансной частоте сопротивление контура равно:
Rо = pQ , где р - это характеристическое сопротивление колебательного контура, численно равное: р = √ L/C , а
Q = fо/Δf - это параметр добротности LC контура, определяющий полосу пропускания фильтра по уровню 3 дБ.
Рис.1
А рассчитать добротность контура можно по формуле Q = p/Rпот = (√ L/C )/Rпот ,
где Rпот - это сумма сопротивлений потерь:
а) в катушке индуктивности (в первом приближении = активному сопротивлению катушки) и
б) в конденсаторе (сопротивление потерь в диэлектрике).
На низких частотах конденсаторы практически не вносят потерь, поэтому добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления катушки. Чем ниже частота, тем больше витков и тоньше провод, тем проще его измерить активное сопротивление тестером.
На радиочастотах значение активного сопротивления катушки может составлять доли ома. Поэтому для расчёта добротности надо: либо найти сопротивление катушки в Омах по формуле R= 4ρ*L/(πd²), где ρ — удельное сопротивление меди, равное 0,017 Ом•мм²/м, L - длина в метрах, d - диаметр провода в мм. Либо (и лучше) - вооружиться генератором сигналов, каким-либо измерителем уровня выходного сигнала с высоким внутренним сопротивлением, и определить добротность контура экспериментально.
Это решение является более правильным в связи с тем, что на высоких частотах на сопротивление потерь начинают влиять и другие факторы, в частности потери в конденсаторе, особенно если он окажется варикапом.
Нарисуем табличку с расчётом фильтра для низкочастотных приложений.
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ НЧ.
Если параметр активного сопротивления катушки R опущен, его значение принимается равным 100 Омам.
Необходимо отметить, что все полученные в таблице данные верны и для последовательного колебательного контура. При этом, если мы хотим использовать свойства контура полностью, т. е. получить острую резонансную кривую, соответствующую конструктивной добротности, то параллельный контур надо нагружать слабо, выбирая R1 и Rн намного больше Rо (на практике десятки-сотни кОм), для последовательного же контура, сопротивление генератора R1 наоборот должно быть на порядки меньше характеристического сопротивления ρ.
Теперь, нарисуем таблицу для расчёта высокочастотных резонансных контуров.
Тут на добротность влияет не только активное сопротивление катушек, но и другие факторы, такие как - потери в ферритах, наличие экрана, эффект близости витков и т. д. Поэтому вводить этот параметр в качестве входного я не стану - будем считать, что добротность катушки вы измерили, или подсмотрели в документации на готовые катушки. Естественным образом значение добротности катушки должно измеряться на резонансной частоте контура, ввиду прямой зависимости этой величины от рабочей частоты (Q=2πfL/R).
К тому же я добавлю сюда параметр добротности конденсатора, особенно актуальный в случае применения варикапов.
По умолчанию (для желающих оставить эти параметры без внимания), добротность катушки примем равной 100, конденсатора - 1000, а для испытывающих стремление измерить эти параметры в радиолюбительских условиях, рекомендую посетить страницу ссылка на страницу .
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ ВЧ.
Теперь плавно переходим к LC фильтрам верхних и нижних частот (ФВЧ и ФНЧ).
«Добротность обозначается символом Q (от английского quality factor) и является тем параметром колебательной системы, который определяет ширину резонанса и характеризует, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан.
Да уж. Напустили тумана ироды - без поллитры не разберёшься. А ведь придётся, раз впряглись.
Так вот. К чему это я?
А к тому, что для получения в сухом остатке высокодобротного колебательного контура, придётся поискать в загашнике и высококачественный конденсатор с низким током утечки, и катушку индуктивности - крепкую, добротную и красивую, словно выпавшую из картины венецианского мастера в Пушкинском музее.
Приведём эквивалентную схему колебательного контура.
Здесь L и C - собственные индуктивность и ёмкость компонентов, входящих в состав колебательного контура,
rL - сопротивление катушки, эквивалентное потерям электрической энергии в проводе катушки индуктивности,
Rш - сумма сопротивлений, обусловленных потерями в изоляции провода, каркасе, экране, сердечнике катушки индуктивности, а также потерями, вызванные наличием токов утечки в конденсаторе.
При подключении к контуру внешних цепей, параллельно Rш добавляется дополнительное сопротивление Rн, вносимое этими внешними цепями.
По большому счёту, на Рис.1 не хватает ещё одной ёмкости, равной сумме паразитных ёмкостей катушки индуктивности, внешних цепей и паразитной ёмкости монтажа. На высоких частотах эти привнесённые ёмкости могут иметь существенные величины, соизмеримые с ёмкостью самого контурного конденсатора. На добротность эти ёмкости существенного влияния не оказывают, но при расчёте резонансной частоты их необходимо учитывать и суммировать со значением основной ёмкости С.
Теперь давайте разберёмся, что такое "скорость затухания собственных колебаний в системе" и, каким боком она связана с добротностью.
Для начала мысленно спаяем схему, нарисованную на Рис.1, и замкнём переключатель на батарейку (в левое по схеме положение).
Конденсатор С зарядится до уровня, равного напряжению питания.
Теперь перещёлкнем переключатель в правое по схеме положение.

Благодаря энергии, запасённой в конденсаторе, в образовавшейся LC-цепи возникнут свободные колебания на частоте резонанса колебательного контура, равной fо= 1/2π√ LС .
Поскольку у нас ни с какой стороны не вечный двигатель - свободные колебания затухают, причём скорость затухания зависит от потерь в конденсаторе и катушке индуктивности: чем они меньше, тем медленнее затухание.
Число колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в е π = 23,14 раза, как раз и будет числено равняться добротности контура Q.
Число периодов свободных колебаний в контуре можно подсчитать счётчиком импульсов и таким образом узнать добротность колебательного контура, генератор сигналов в этом случае не нужен.
Собственно говоря, на таком принципе и строится большинство промышленных измерителей добротности.
Рисуем резонансную кривую (амплитудно частотную характеристику) колебательного контура.
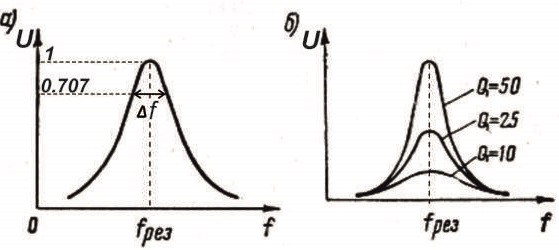
По частотной характеристике условно определяется полоса пропускания контура Δf.
При этом сделано допущение, что напряжение внутри этой полосы имеет право снижаться до уровня 0,707 от максимального.
Исходя из этого, формула для определения добротности приобретает следующий вид: Q = f рез/Δf .
Рис.2
Из формулы естественным образом вытекает, что чем выше добротность - тем уже полоса пропускания резонансного контура, соответственно, чем ниже - тем шире.
А как измерить добротность контура, не прибегая к изготовлению специальных устройств, в домашней лаборатории?
1. Если речь идёт о низких (звуковых) частотах, то тут всё просто.
В этом случае, Q равна отношению реактивного сопротивления индуктивного или ёмкостного характера (характеристического сопротивления) к полному последовательному сопротивлению потерь в резонансном контуре. В виду того, что конденсаторы на данных частотах практически не вносят потерь, то добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления катушки.
А поскольку данное сопротивление можно легко измерить обычным омметром, то имеет полный смысл проделать эту не сильно замысловатую манипуляцию, после чего перейти на страницу ссылка на страницу и в первой таблице произвести расчёт добротности. Естественным образом, подразумевается, что катушка намотана на соответствующем для данных частот сердечнике, не вносящих существенных потерь в работу колебательного контура.
2. На высоких частотах (радиочастотах) значение активного сопротивления катушки может составлять доли ома, к тому же возможно проявление влияния добротности конденсатора на общую добротность цепи, поэтому такими же примитивными методами, как в случае НЧ обойтись не удастся.
Рискну сделать осторожное предположение, что в радиолюбительской лаборатории у нас затерялся высокочастотный генератор с 50-омным выходом и такой же высокочастотный осциллограф, или, на худой конец, измеритель ВЧ напряжений.
В этом случае мы воспользуемся ещё одним определением Q. Добротность резонансного контура равна фактору увеличения напряжения и может быть выражена отношением напряжения, развиваемого на реактивных элементах к входному напряжению, поданному последовательно с контуром.
Спаяем пару резисторов.
Добротность измеряется при настройке генератора сигналов на частоту резонанса контура, соответствующую максимальному выходному напряжению.
Добротность Q рассчитывается как отношение выходного напряжения на резонансном контуре к напряжению, поданному на него.
В нашем случае Q = 250 x V2/V1 .
Рис.3
Так как в случае высокодобротных элементов, сопротивление контура на резонансной частоте может превышать значение в сотню килоом, для корректного измерения добротности, входные импедансы измерителя ВЧ напряжений, либо осциллографа должны превышать это значение как минимум на порядок.
Все наши рассуждения и формулы корректны для ненагруженных параллельных колебательных контуров, то есть для случаев, когда на выходе отсутствует реальная нагрузка.
В реальной схеме контур связан с источником колебаний и нагрузкой, которые вносят в него дополнительные потери, снижающие добротность.
Эквивалентная добротность Q параллельного колебательного контура с учётом этих потерь вычисляется по следующей формуле: Q = Q0 x Rш/(Rш+Rо) , где
Q0 - добротность ненагруженного контура,
Rш - шунтирующее сопротивление, равное R(источника) ll R(нагрузки),
Rо - эквивалентное сопротивление ненагруженного контура, равное сопротивлению контура на резонансной частоте, значение которого можно посчитать на той же странице ссылка на страницу во 2-ой таблице.
А на следующей странице порассуждаем на тему: что надо сделать, чтобы намотать катушку с максимально-возможной добротностью.
Электрическая цепь — предназначена не только для передачи тока и напряжения от источника к потребителю. В данной электроцепи возникают определенные физические процессы, которые связаны с влиянием ее элементов на протекание данного тока.

В этой статье будет описано, что такое добротность контура. Кроме того будет приведена формула для расчета этой величины, схемы последовательного и параллельного контуров.
Определение
Физика дает следующее определение добротности. Добротностью называют параметр колебательной системы, который определяет ширину резонанса и характеризует, насколько запасы энергии в системе больше возникающих ее потерь во время изменения фазы на один радиан. Дело в том, что данный показатель определяет разницу вынужденных колебаний при резонансе с определенной амплитудой колебаний на каком-то удалении от места резонанса. При этом амплитуда вынужденных колебаний не имеет никакой зависимости от их частоты. Параметр находит применение не только при расчетах электрических цепей. Его применяют так же в механике, акустике и химии.


Получается, что колебательный контур является разницей между входящим реактивным сопротивлением и выходящим активным. Если в колебательном контуре имеется емкость C, индуктивность L и нагрузка R, то для расчета Q используется формула:
В данной формуле за резонансную частоту электроцепи ω0 отвечает показатель 1/R.
Параметр добротности измеряется при настройке генератора электросигналов на частоту резонансных колебаний. Сама частота резонанса равна максимальному выходному напряжению такой цепи.
Параллельный контур
Добротность любого параллельного колебательного контура предполагает наличие цепи, в которой имеется емкость, нагрузка и индуктивность, соединенные параллельно. Они образуют так называемую RLC-схему.

Определяющая величина для такой схемы — это проводимость конденсатора с катушкой. Именно она суммируется при расчетах и является реактивной проводимостью параллельного колебательного контура. На резонансной частоте проводимость катушки с конденсатором будут равны, а общая разница при этом равняется 0. Для расчета такой цепи используется формула:

При этом стоит учитывать следующее:
- Не принимается во внимание емкостная паразитная характеристика катушки индуктивности, но учитывается добротность индуктивного элемента. Она соответствует выражению:
- Также учитывается добротность конденсатора, использующегося в такой электроцепи. Потери в конденсаторе связаны с наличием диэлектрика в его конструкции. Добротность конденсатора вместе с имеющимися потерями, напрямую связаны с потерями энергии на его диэлектрике tgδ. Данный коэффициент определяем с помощью такого выражения:
- На резонансной частоте к переменному току прилагается бесконечное сопротивление.
- В реальной RLC-цепи отсутствует бесконечное сопротивление, но этот параметр при увеличении сопротивления контура значительно снижается.
В параллельном колебательном контуре резонансная частота является той частотой, при которой реактивное сопротивление равняется 0, а величина входящего сопротивления является активным. Отсюда можно сделать вывод, что отсутствует фазовый сдвиг между током и напряжением.
Последовательный контур
Для последовательного колебательного контура характерно наличие последовательного соединения емкости с индуктивностью. При этом эти два элемента не влияют на потери энергии в цепи и являются идеальными элементами.

Потери в данной схеме вызваны только наличием активной нагрузки. Ниже представлен график амплитудно-частотной характеристики такой схемы.

Для такой цепи сопротивление катушки и конденсатора являются паразитными, приводят к появлению резонанса. Данный резонанс выравнивает или обнуляет сопротивления, оставляя только влияние активной нагрузки R от резистора. При этом добротность такой электроцепи определяется, как разницу напряжений на источнике тока и выходах катушки/конденсатора. В этом случае Q определяют с помощью следующего выражения:

В данной формуле:
- С — емкость конденсатора.
- L — индуктивность катушки.
- R — потери сопротивления.
Для примера попробуем решить следующую задачу. В цепи имеется катушка индуктивности L=100 мГн с сопротивлением R=100 Ом, которая соединена последовательно с конденсатором емкостью C=0.07 мкФ. Найдите резонансную частоту ω0, характеристическое сопротивление и добротность колебательного контура.
Вычисляем резонансную частоту контура:

Определяем характеристическое сопротивление:

Конечный шаг — вычисление добротности контура:

Заключение
В статье было дано краткое описание, что такое добротность контура и чему параметр равен для различных вариантов контура (параллельного, последовательного). Данная характеристика цепи и ее составных элементов играет ключевое значение при определении потерь от включения в нее различных конденсаторов, катушек и активных резисторов. С помощью добротности можно определить разницу между входным и выходным напряжениями электроцепи.
Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.
Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.
Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения:
где r - коэффициент сопротивления среды. Знак минус показывает, что FC направлена в сторону противоположную скорости.
Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r. По второму закону Ньютона
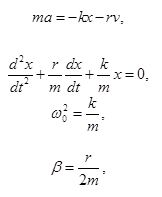
где β - коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.
- дифференциальное уравнение затухающих колебаний.
- уравнение затухающих колебаний.
ω – частота затухающих колебаний: Период затухающих колебаний:
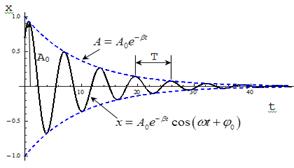
Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало. Если затухания выражены слабо (β→0), то
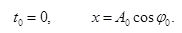
Затухающие колебания можно рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону В уравнении (1) А0 и φ0 - произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз
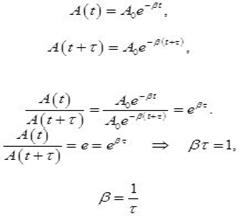
τ - время релаксации.
Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D, который равен отношению амплитуд, отстоящих по времени на период:
Логарифмический декремент затухания равен логарифму D:
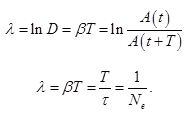
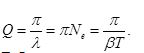
Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания - постоянная для данной системы величина. Еще одной характеристикой колебательной система является добротность Q.
Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ. Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии. Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.
Последовательный колебательный контур является простейшей резонансной (колебательной) цепью. Состоит последовательный колебательный контур, из последовательно включенных катушки индуктивности и конденсатора. При воздействии на такую цепь переменного (гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина которого вычисляется по закону Ома: I = U / ХΣ , где ХΣ - сумма реактивных сопротивлений последовательно включенных катушки и конденсатора (используется модуль суммы).
Для освежения памяти, вспомним как зависят реактивные сопротивления конденсатора и катушки индуктивности от частоты приложенного переменного напряжения. Для катушки индуктивности, эта зависимость будет иметь вид:
Из формулы видно, что при увеличении частоты, реактивное сопротивление катушки индуктивности увеличивается. Для конденсатора зависимость его реактивного сопротивления от частоты будет выглядеть следующим образом:
В отличии от индуктивности, у конденсатора всё происходит наоборот - при увеличении частоты, реактивное сопротивление уменьшается
. На следующем рисунке графически представлены зависимости реактивных сопротивлений катушки XL и конденсатора ХC от циклической (круговой) частоты ω, а также график зависимости от частоты ω их алгебраической суммы ХΣ. График, по сути, показывает зависимость от частоты общего реактивного сопротивления последовательного колебательного контура.
Из графика видно, что на некоторой частоте ω=ωр , на которой реактивные сопр отивления катушки и конденсатора равны по модулю (равны по значению, но противоположны по знаку), общее сопротивление цепи обращается в ноль. На этой частоте в цепи наблюдается максимум тока, который ограничен только омическими потерями в катушке индуктивности (т.е. активным сопротивлением провода обмотки катушки) и внутренним сопротивлением источника тока (генератора). Такую частоту, при которой наблюдается рассмотренное явление, называемое в физике резонансом, называют резонансной частотой или собственной частотой колебаний цепи. Также из графика видно, что на частотах, ниже частоты резонанса реактивное сопротивление последовательного колебательного контура носит емкостной характер, а на более высоких частотах - индуктивный. Что касается самой резонансной частоты, то она может быть вычислена при помощи формулы Томсона, которую мы можем вывести из формул реактивных сопротивлений катушки индуктивности и конденсатора, приравняв их реактивные сопротивления друг к другу:
На рисунке справа, изображена эквивалентная схема последовательного резонансного контура с учетом омических потерь R, подключенного к идеальному генератору гармонического напряжения с амплитудой U. Полное сопротивление (импеданс) такой цепи определяется: Z = √(R 2 +XΣ 2 ), где XΣ = ω L-1/ωC. На резонансной частоте, когда величины реактивных сопротивлений катушки XL = ωL и конденсатора ХС= 1/ωС равны по модулю, величина XΣ обращается в нуль (следовательно, сопротивление цепи чисто активное), а ток в цепи определятся отношением амплитуды напряжения генератора к сопротивлению омических потерь: I= U/R. При этом на катушке и на конденсаторе, в которых запасена реактивная электрическая энергия, падает одинаковое напряжение UL = UС = IXL = IXС.
На любой другой частоте, отличной от резонансной, напряжения на катушке и конденсаторе неодинаковы - они определяются амплитудой тока в цепи и величинами модулей реактивных сопротивлений XL и XС.Поэтому резонанс в последовательном колебательном контуре принято называть резонансом напряжений. Резонансной частотой контура называют такую частоту, на которой сопротивление контура имеет чисто активный (резистивный) характер.Условие резонанса - это равенство величин реактивных сопротивлений катушки индуктивности и ёмкости.
Одними из наиболее важных параметров колебательного контура (кроме, разумеется, резонансной частоты) являются его характеристическое (или волновое) сопротивление ρ и добротность контура Q. Характеристическим (волновым) сопротивлением контура ρ называется величина реактивного сопротивления емкости и индуктивности контура на резонансной частоте: ρ = ХL = ХC при ω =ωр . Характеристическое сопротивление может быть вычислено следующим образом: ρ = √(L/C). Характеристическое сопротивление ρ является количественной мерой оценки энергии, запасенной реактивными элементами контура - катушкой (энергия магнитного поля) WL = (LI 2 )/2 и конденсатором (энергия электрического поля) WC=(CU 2 )/2. Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью Q контура, что в буквальном переводе с английского языка обозначает "качество". Добротность колебательного контура - характеристика, определяющая амплитуду и ширину АЧХ резонанса и показывающая, во сколько раз запасы энергии в контуре больше, чем потери энергии за один период колебаний. Добротность учитывает наличие активного сопротивления нагрузки R.
Для последовательного колебательного контура в RLC цепях, в котором все три элемента включены последовательно, добротность вычисляется:

где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно. Величину, обратную добротности d = 1 / Q называют затуханием контура. Для определения добротности обычно пользуются формулой Q = ρ / R, где R-сопротивление омических потерь контура, характеризующее мощность резистивных (активных потерь) контура Р = I 2 R. Добротность реальных колебательных контуров, выполненных на дискретных катушках индуктивности и конденсаторах, составляет от нескольких единиц до сотни и более. Добротность различных колебательных систем, построенных на принципе пьезоэлектрических и других эффектов (например, кварцевые резонаторы) может достигать нескольких тысяч и более.
Частотные свойства различных цепей в технике принято оценивать с помощью амплитудно-частотных характеристик (АЧХ), при этом сами цепи рассматривают как четырёхполюсники. На рисунках ниже представлены два простейших четырехполюсника, содержащих последовательный колебательный контур и АЧХ этих цепей, которые приведены (показаны сплошными линями). По вертикальной оси графиков АЧХ отложена величина коэффициента передачи цепи по напряжению К, показывающая отношение выходного напряжения цепи к входному.
Для пассивных цепей (т.е. не содержащих усилительных элементов и источников энергии), величина К никогда не превышает единицу. Сопротивление переменному току изображённой на рисунке цепи, будет минимально при частоте воздействия, равной резонансной частоте контура. В этом случае коэффициент передачи цепи близок к единице (определяется омическими потерями в контуре). На частотах, сильно отличающихся от резонансной, сопротивление контура переменному току достаточно велико, а следовательно, и коэффициент передачи цепи будет падать практически до нуля.
При резонансе в этой цепи, источник входного сигнала оказывается фактически замкнутым накоротко малым сопротивлением контура, благодаря чему коэффициент передачи такой цепи на резонансной частоте падает практически до нуля (опять-таки в силу наличия конечного сопротивления потерь). Наоборот, при частотах входного воздействия, значительно отстоящих от резонансной, коэффициент передачи цепи оказывается близким к единице. Свойство колебательного контура в значительной степени изменять коэффициент передачи на частотах, близких к резонансной, широко используется на практике, когда требуется выделить сигнал с конкретной частотой из множества ненужных сигналов, расположенных на других частотах. Так, в любом радиоприемнике при помощи колебательных цепей обеспечивается настройка на частоту нужной радиостанции. Свойство колебательного контура выделять из множества частот одну принято называть селективностью или избирательностью. При этом интенсивность изменения коэффициента передачи цепи при отстройке частоты воздействия от резонанса принято оценивать при помощи параметра, называемого полосой пропускания. За полосу пропускания принимается диапазон частот, в пределах которого уменьшение (или увеличение - в зависимости от вида цепи) коэффициента передачи относительно его значения на резонансной частоте, не превышает величины 0,7 (3дБ).
Пунктирными линиями на графиках показаны АЧХ точно таких же цепей, колебательные контуры которых имеют такие же резонансные частоты, как и для случая рассмотренного выше, но обладающие меньшей добротностью (например, катушка индуктивности намотана проводом, обладающим большим сопротивлением постоянному току). Как видно из рисунков, при этом расширяется полоса пропускания цепи и ухудшаются ее селективные (избирательные) свойства. Исходя из этого, при расчете и конструировании колебательных контуров нужно стремиться к повышению их добротности. Однако, в ряде случаев, добротность контура, наоборот, приходится занижать (например, включая последовательно с катушкой индуктивности резистор небольшой величины сопротивления), что позволяет избежать искажений широкополосных сигналов. Хотя, если на практике требуется выделить достаточно широкополосный сигнал, селективные цепи, как правило, строятся не на одиночных колебательных контурах, а на более сложных связанных (многоконтурных) колебательных системах, в т.ч. многозвенных фильтрах.
Читайте также:

