Что такое лямбда в гидравлике

Обновлено: 08.01.2025

Любой расчет гидравлических систем выполняется на определенной основе, в этой статье мы рассмотрим методы, и формулы на которых базируются расчеты гидравлических систем. Для гидравлического расчета трубопровода вы можете воспользоваться калькулятором гидравлического расчета трубопровода.

Потери напора на трение .

Всем известно, что при движении жидкости по трубопроводу возникают постери напора на трение. В случае, когда движении жидкости в трубах равномерное, то потери давления на трение как при ламинарном, так и при турбулентном режимах движения можно рассчитать по формуле Дарси–Вейсбаха:

D ρ тр = λ· l / d · ρ · V 2 /2

l – коэффициент гидравлического трения;
l –длина трубопровода;
d – диаметр трубопровода;
r – плотность жидкости;
V – средняя скорость течения жидкости.

Коэффициент гидравлического трения будет зависеть от режима движения жидкости, значения критерия Рейнольдса:

Re = Vd/ν

А так же коэффициент гидравлического трения будет зависеть от состояния стенок трубы, которое характеризуется относительной шероховатостью:

D ̅ = D ,/d ,

D_э – эквивалентная равномерно-зернистая шероховатость (то есть такая высота неровностей, которые образовани песчинками одинакового размера, которая при расчете дает одинаковое с действительной шероховатостью значение коэффициента гидравлического трения).

При ламинарном режиме течения жидкости коэффициент гидравлического трения можно рассчитать по формуле:

λ = 64/Re .

При турбулентном режиме течения жижкости весь диапазон значений чисел Рейнольдса, в зависимости от относительной шероховатости, необходимо разделить на области, каждой из которых будет соответствовать своя формула для расчета коэффициента гидравлического трения:

область гидравлически гладких труб 2300 ≤ Re ≤ 10 √D:

1. λ = 0.3164/Re 0.25 – формула Блазиуса;

2. 10/D̅ ≤ Re ≤ 500√D – переходная область;

3. λ = 0.11 · (D̅ + 68/Re) 0.25 – формула А.Д. Альтшуля;

4. Re > 500√D – квадратичная область;

5. λ = 0.11 · D -0.25 – формула Б.Л. Шифринсона.

Если жидкость будет протекать по трубам, форма поперечного сечения которых не будет круглой, то в приведенных выше формулах будет использоваться вместо d эквивалентный диаметр:

d, = 4S/ П ,

где S – площадь поперечного сечения трубы; П – полный смоченный периметр трубы.

Коэффициент гидравлического трения при ламинарном течении в трубах различной формы можно рассчитать по формуле

λ = A/Re ,

где А – коэффициент, численное значение которого зависит от формы поперечного сечения трубы.

Сифон - это соединяющий два резервуара трубопровод, часть которого находится выше уровня жидкости в напорном резервуаре. Допустимое возвышение верхней точки сифона вычисляют по формуле

h o = p α - D p ’/ ρg

где Dp’– потеря давления на участке от напорного резервуара до верхней точки сифона.

Минимально допустимое давление в верхней точке сифона должно быть выше давления насыщения при данной температуре.

Пропускная способность трубопроводов в период эксплуатации снижается. Вследствие коррозии и образования отложений в трубах шероховатость их увеличивается, что в первом приближении можно оценить по формуле:

D , = D 0 + αt ,

где D_о – абсолютная шероховатость новых труб, мм;
D_t – абсолютная шероховатость через t лет эксплуатации, мм;
a – коэффициент, характеризующий быстроту возрастания шероховатости, мм/год.

Местные потери давления в трубах .

Местные сопротивления, к которым относится арматура, фасонные части трубопроводов и прочее оборудование, могут вызывать изменения величины и (или) направления скорости движения жидкости на определенных участках трубопровода, что неизбежно приводит к потерям давления в этих трубах. Потери давления определяют по формуле Вейсбаха:

D p ж = ζρ V 2 /2 .

Значения коэффициентов местных сопротивлений V зависят от конфигурации местного сопротивления и режима течения жидкости перед ним.

При резком сужении трубопровода (резком изменении площади проходного сечения от S₁ до S₂) коэффициент местного сопротивления рассчитывается по формуле:

ζ o = (1/G – 1) 2 ,

где e – коэффициент сжатия струи, который можно определить по формуле А.Д. Альтшуля:

G = 0.57 + 0.043/(1.1 – n) , где: n = S 2 /S 1 .

Коэффициент местного сопротивления диафрагмы, которая располагается внутри трубы постоянного сечения (отнесенный к сечению трубопровода):

ζ д = (1 /n д G – 1) 2 ,

При движении жидкости с малыми числами Рейнольдса коэффициенты местных сопротивлений ориентировочно определяют по формуле А.Д. Альтшуля:

ζ = A / Re + ζ L

где ζ_L – значение коэффициента местного сопротивления в квадратичной области; Re – число Рейнольдса, отнесенное к нестесненному сечению трубопровода.

В случаях, когда расстояние между отдельными местными сопротивлениями довольно велико для того, чтобы искажение эпюры скоростей, вызванное одним из них, не сказывалось на следующем, потери давления во всех местных сопротивлениях суммируются. Для этого необходимо, чтобы местные сопротивления отстояли друг от друга на расстояние, превышающее l_вл, определяемое по формулам:

Формула Дарси — формула, определяющая потери напора или потери давления на гидравлических сопротивлениях:

$\Delta h = \xi \cdot \frac<V^2> $

$\frac<V^2> <ul> <li>Δh — потери напора на гидравлическом сопротивлении;</li> <li>ξ — коэффициент потерь (коэффициент Дарси;</li> <li>V — средняя скорость течения жидкости;</li> <li>g — ускорение свободного падения;</li> <li>величина$
называется скоростным напором.

Формула Дарси, определяющая потери давления на гидравлических сопротивлениях, имеет вид:

$\Delta P = \xi \cdot \frac<V^2> \cdot \rho$

ΔP — потери давления на гидравлическом сопротивлении;
ρ — плотность жидкости.

Содержание

Формула Дарси-Вейсбаха

Если гидравлическое сопротивление представляет собой участок трубы длиной L и диаметром D , то коэффициент Дарси определяется следующим образом:

$\xi = \lambda \cdot \frac<L> $

где λ — коэффициент потерь на трение по длине.

Тогда формула Дарси приобретает вид:

$\Delta h = \lambda \cdot \frac<L> \cdot \frac$

или для потери давления:

$\Delta P = \lambda \cdot \frac<L> \cdot \frac \cdot \rho$

Последние две зависимости получили название формулы Дарси-Вейсбаха.

Если определяются потери на трение по длине для трубы некруглого поперечного сечения, то D представляет собой гидравлический диаметр.

Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.

Определение коэффициента потерь на трение по длине

Коэффициент λ определяется по разному для разных случаев.

Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле:

$\lambda = \frac<64> <\mathrm<Re>>,$

Иногда для гибких труб в расчётах приниают

$\lambda = \frac<68> <\mathrm<Re>>.$

Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:

$\lambda = \frac<0,316> <\sqrt[4]<\mathrm<Re>>>.$

Эта формула даёт хорошие результаты при числах Рейнольдса, изменяющихся в пределах от критического числа Рейнольдса Re_кр до значений Re = 10 5 . Формула Блазиуса применяется для гидравлически гладких труб.

Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).

Определение коэффициента Дарси для местных сопротивлений

Рис. 1. Гидравлический конфузор: Q₁ — поток жидкости в широком сечении трубы; Q₂ — поток жидкости в узком сечении трубы

Для каждого вида местных сопротивлений существуют свои зависимости для определения коэффициента ξ .

К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.

1. При внезапном расширении трубы:

$\xi = \left( 1 - \frac<S_1> \right)^2 ,$

где S₁ и S₂ — площади поперечного сечения трубы, соответственно перед расширением и после него.

2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:

$\xi = \frac<1 -S_2/S_1> ,$

где S₁ и S₂ — площади поперечного сечения трубы, соответственно, перед сужением и после него.

3. При постепенном сужении трубы (конфузор):

$\xi =\frac<\lambda_T> > \left( 1-\frac \right)$
,

$n =\frac<S_1> где$
— степень сужения; λ_T — коэффициент потерь на трение по длине при турбулетном режиме.

4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).

См. также

Литература

Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/ Т.М. Башта, С.С. Руднев, Б.Б. Некрасов и др. — 2-е изд., перераб. – М.: Машиностроение, 1982.
Гейер В.Г., Дулин В.С., Заря А.Н. Гидравлика и гидропривод: Учеб для вузов. — 3-е изд., перераб. и доп. — М.: Недра, 1991.

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое "Формула Дарси-Вейсбаха" в других словарях:

Формула Дарси — Формула Вейсбаха[1] в гидравлике эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом (англ.) в 1855… … Википедия

ДАРСИ — ВЕЙСБАХА ФОРМУЛА — (в гидравлике), определяет величину потерь напора на трение при движении жидкости в трубах: hv=(ll/d)(v2/2g), где l коэфф. гидравлич. трения, l и d длина и диаметр трубы, ч ср. скорость течения жидкости, g ускорение свободного падения. Коэфф. l… … Физическая энциклопедия

ДАРСИ - ВЕЙСБАХА ФОРМУЛА — в гидравлике определяет величину потерь напора на трение при движении жидкости в трубах: , где коэф. гидравлич. трения, l и d длина и диаметр трубы, v ср. скорость течения жидкости, g ускорение свободного падения. Коэф. зависит от характера… … Физическая энциклопедия

Формула Шези — Формула Шези формула для определения средней скорости потока при установившемся равномерном турбулентном движении жидкости в области квадратичного сопротивления для случая безнапорного потока. Опубликована французским инженером гидравликом… … Википедия

Формула Прони — Формула Прони это исторически важная формула в гидравлике, применявшаяся для расчётов потерь напора на трение при течении жидкости по трубам. Это эмпирическая формула, полученная французом Гаспаром де Прони в XIX веке: где hf потери… … Википедия

Дарси, Анри — Анри Дарси Henry Darcy Дата рождения … Википедия

Формула Борда — В гидродинамике, формула (теорема) Борда Карно это эмпирическая формула, описывающая потери энергии (или напора) жидкости, происходящие при местном расширении потока. Эта формула, в отличие от уравнения Бернулли для идеальной жидкости … Википедия

Гидравлические потери — или гидравлическое сопротивление безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения[1][2].… … Википедия

Диффузор (гидроаэродинамика) — У этого термина существуют и другие значения, см. Диффузор. Диффузор (в гидроаэродинамике) часть канала (трубы), в которой происходят замедление (расширение) потока. При этом перепад статических давлений на диффузоре может быть меньше, чем… … Википедия

Гидравлический диаметр — Гидравлический диаметр мера эффективности русла в пропускании потока жидкости. Чем меньше гидравлический диаметр, тем большее сопротивление потоку оказывает русло (при одинаковой площади поперечного сечения потока). Определяется по формуле … Википедия

Потери энергии (уменьшение гидравлического напора) можно наблюдать в движущейся жидкости не только на сравнительно длинных участках, но и на коротких. В одних случаях потери напора распределяются (иногда равномерно) по длине трубопровода - это линейные потери; в других - они сосредоточены на очень коротких участках, длиной которых можно пренебречь, - на так называемых местных гидравлических сопротивлениях: вентили, всевозможные закругления, сужения, расширения и т.д., короче всюду, где поток претерпевает деформацию. Источником потерь во всех случаях является вязкость жидкости.

Следует заметить, что потери напора и по длине и в местных гидравлических сопротивлениях существенным образом зависят от так называемого режима движения жидкости.

При наблюдении за движением жидкости в трубах и каналах, можно заметить, что в одном случае жидкость сохраняет определенный строй своих частиц, а в других - перемещаются бессистемно. Однако исчерпывающие опыты по этому вопросу были проведены Рейнольдсом в 1883 г. На рис. 4.1 изображена установка, аналогичная той, на которой Рейнольдс производил свои опыты.

Установка состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С на конце, и сосуда D с водным раствором краски, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.

Первый случай движения жидкости. Если немного приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить краску в поток воды, то увидим, что введенная в трубу краска не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Если при этом, если к трубе подсоединить пьезометр или трубку Пито, то они покажут неизменность давления и скорости по времени. Такой режим движения называется ламинарный.

Второй случай движения жидкости. При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка краски по выходе из трубки начинает колебаться, затем размывается и перемешивается с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито при этом покажут непрерывные пульсации давления и скорости в потоке воды. Такое течение называется турбулентным (рис.4.1, вверху).

Если уменьшить скорость потока, то восстановится ламинарное течение.

Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.

Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической υ _кр.

Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.

Как показывает опыт, для труб круглого сечения Re_кр примерно равно 2300.

Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re < Re_кр течение является ламинарным, а при Re > Re_кр течение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равно 4000, а при Re = 2300…4000 имеет место переходная, критическая область.

Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубопроводов.

В некоторых случаях при движении жидкости в закрытых руслах происходит явление, связанное с изменением агрегатного состояния жидкости, т.е. превращение ее в пар с выделением из жидкости растворенных в ней газов.

Наглядно это явление можно продемонстрировать на простом устройстве, состоящим из трубы, на отдельном участке которой установлена прозрачная трубка Вентури (рис.4.2). Вода под давлением движется от сечения 1-1 через сечение 2-2 к сечению 3-3. Как видно из рисунка, сечение 2-2 имеет меньший диаметр. Скорость течения жидкости в трубе можно изменять, например, установленным после сечения 3-3 краном.

При небольшой скорости никаких видимых изменений в движении жидкости не происходит. При увеличении скорости движения жидкости в узком сечении трубки Вентури 2-2 появляется отчетливая зона с образованием пузырьков газа. Образуется область местного кипения, т.е. образование пара с выделением растворенного в воде газа. Далее при подходе жидкости к сечению 3-3 это явление исчезает.

Это явление обусловлено следующим. Известно, что при движении жидкой или газообразной среды, давление в ней падает. Причем, чем выше скорость движения среды, тем давление в ней ниже. Поэтому, при течении жидкости через местное сужение 2-2, согласно уравнению неразрывности течений, увеличивается скорость с одновременным падением давления в этом месте. Если абсолютное давление при этом достигает значения равного давлению насыщенных паров жидкости при данной температуре или значения равного давлению, при котором начинается выделение из нее растворимых газов, то в данном месте потока наблюдается интенсивное парообразование (кипение) и выделение газов. Такое явление называется кавитацией.

При дальнейшем движении жидкости к сечению 3-3, пузырьки исчезают, т.е. происходит резкое уменьшение их размеров. В то время, когда пузырек исчезает (схлопывается), в точке его схлопывания происходит резкое увеличение давления, которое передается на соседние объемы жидкости и через них на стенки трубопровода. Таким образом, от таких многочисленных местных повышений давлений (гидроударов), возникает вибрация.

Таким образом, кавитация - это местное нарушение сплошности течения с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в потоке.

Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Кавитация возникает в кранах, вентилях, задвижках, жиклерах и т.д.

Кавитация может иметь место в гидромашинах (насосах и гидротурбинах), снижая при этом их коэффициент полезного действия, а при длительном воздействии кавитации происходит разрушение деталей, подверженных вибрации. Кроме этого разрушаются стенки трубопроводов, уменьшается их пропускная способность вследствие уменьшения живого сечения трубы.

Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью - квадратичную параболу (рис.4.3).

Уравнение, связывающее переменные υ и r, имеет следующий вид:

где P1 и P2 - давления соответственно в сечениях 1 и 2.

У стенок трубы величина r = R, , значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной

Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.

Максимальная скорость дает высоту параболоида

Как известно из геометрии, объем параболоида высотой h и площадью ρR 2 равен

а в нашем случае

Если вместо R подставить диаметр трубы d, то формула (4.4) приобретет вид

Расход в трубе можно выразить через среднюю скорость:

Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.4.3).

Потеря давления в трубопроводе будет равна

Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ ( μ = υ ρ ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:

Так как левая часть полученного равенства равна потерям напора h_пот в трубе постоянного диаметра, то окончательно это равенство примет вид:

Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:

где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:

Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re < 2300 применять формулу

Как было указано в п.4.1, для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерять пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рис.4.4. Скорость беспорядочно колеблется около некоторого осредненного по времени значения υ _оср, которое данном случае остается постоянным.

Характер линий тока в трубе в данный момент времени отличается большим разнообразием (рис.4.5).

Рис. 4.4. Пульсация скорости в турбулентном потоке. Рис. 4.5. Характер линий тока в турбулентном потоке

При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рис. 4.6. В тонком пристенном слое толщиной δ жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой δ с ламинарным режимом весьма мал по сравнению с турбулентным ядром.

Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является уже приводившаяся выше эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:

Различие заключается лишь в значениях коэффициента гидравлического трения λ. Этот коэффициент зависит от числа Рейнольдса Re и от безразмерного геометрического фактора - относительной шероховатости Δ/d (или Δ/r₀, где r₀ - радиус трубы).

Впервые наиболее исчерпывающей работы по определению были даны И.И. Никурадзе, который на основе опытных данных построил график зависимости lg(1000λ) от lg Re для ряда значений Δ/r ₀. Опыты Никурадзе были проведены на трубах с искусственно заданной шероховатостью, полученной путем приклейки песчинок определенного размера на внутренние стенки трубопровода. Результаты этих исследований представлены на рис. 4.7, где построены кривые зависимости lg (1000λ) от lg Re для ряда значений Δ/r₀.

Прямая I соответствует ламинарному режиму движения жидкости.

Далее на графике можно рассматривать три области.

Первая область - область малых Re и Δ/r₀, где коэффициент λ не зависит от шероховатости, а определяется лишь числом Re (отмечена на рис.4.7 прямой II ). Это область гидравлически гладких труб. Если число Рейнольдса лежит в диапазоне 4000 2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом

2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10). Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.

Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:

где n = S₂/S₁ = ( r₂/r₁ ) 2 - степень расширения диффузора. Потеря напора на расширение h_расш имеет ту же самую природу, что и при внезапном расширении русла

где k - коэффициент смягчения, при α= 5…20°, k = sinα.

Учитывая это полную потерю напора можно переписать в виде:

откуда коэффициент сопротивления диффузора можно выразить формулой

Функция ζ = f(α)имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:

При подстановке в эту формулу λ_Т =0,015…0,025 и n = 2…4 получим α_опт = 6 (рис.4.11).

3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис.4.12).

Полная потеря напора определится по формуле ;

где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:

в которой n = S₁/S₂ - степень сужения.

При выходе трубы из резервуара больших размеров, когда можно считать, что S₂/S₁ = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζ_суж = 0,5.

4. Постепенное сужение русла. Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рис.4.13). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение

где коэффициент сопротивления конфузора определяется по формуле

в которой n = S₁/S₂ - степень сужения.

Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рис.4.14).

5. Внезапный поворот трубы (колено). Данный вид местного сопротивления (рис.4.15) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле

где ζ_кол - коэффициент сопротивления колена круглого сечения, который определяется по графику в зависимости от угла колена δ (рис.4.16).

Рис. 4.15.

Рис. 4.16. Зависимости ζ_кол от угла δ

Рис. 4.17. Отвод

6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d рис.4.17). Коэффициент сопротивления отвода ζ_отв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.

Для отводов круглого сечения с углом δ= 90 и R/d 1 при турбулентном течении можно воспользоваться эмпирической формулой:

Все выше изложенное относится к турбулентному движению жидкости. При ламинарном движении местные сопротивления играют малую роль при определении общего сопротивления трубопровода. Кроме этого закон сопротивления при ламинарном режиме является более сложным и исследован в меньшей степени.

Гидравлическое сопротивление – это сопротивление движению потока рабочей среды, которое оказывается со стороны трубопроводной системы и оценивается количеством потерянной удельной энергии, безвозвратно расходуемой на работу сил трения. При этом гидропотери могут возникать в результате:

Трения по длине. Даже на прямых отрезках трубопровода создаётся противодействие движущемуся потоку. Это возникает на фоне появления сил вязкого трения. Причём с увеличением длины прямолинейного участка повышается сопротивление внутри трубопровода на данном участке.
Местных факторов. Это могут быть повороты, различные сужения, тройники, краны и прочее.

Расчет гидравлического сопротивления и его роль

Любая трубопроводная коммуникация имеет не только прямолинейные участки, но и повороты, ответвления, для создания которых используются различные фитинги. А для регулирования потока рабочей среды устанавливается запорная арматура. Всё это создаёт сопротивление, поэтому очень важно перед тем, как приступать к монтажу трубопровода, необходимо выполнить ряд расчётов, в том числе определить гидравлическое сопротивление. Это позволит в будущем сократить теплопотери и, соответственно, избежать лишних энергозатрат.

Гидравлический расчёт выполняется с целью:

Вычисления потерь давления на конкретных отрезках системы отопления;
Определения оптимального диаметра трубопровода с учётом рекомендованной скорости перемещения рабочего потока;
Расчёта тепловых потерь и величины наименьшего давления в трубопроводе;
Правильного выполнения увязки параллельно расположенных гидравлических ветвей и закреплённой на ней запорной арматуры.

Во время движения по замкнутому контуру рабочему потоку приходится преодолевать определённое гидравлическое сопротивление. Причём с увеличением его значения, должна увеличиваться мощность насоса. Только правильные расчёты помогут выбрать оптимальный вариант насоса. Нет смысла покупать слишком мощное оборудования для трубопроводов с низким гидравлическим сопротивлением, ведь, чем больше мощность, тем выше энергозатраты.

А если мощность будет, наоборот, недостаточной, то насосное оборудование не сможет обеспечить достаточный напор теплоносителя, что приведёт к увеличению тепловых потерь.

Коэффициент гидравлического сопротивления трубы

Это безмерная величина, показывающая, каковы потери удельной энергии.

Ламинарное перемещение рабочего потока

При ламинарном (равномерном) перемещении рабочей среды по трубопроводу круглого сечения потери давления по длине вычисляется по формуле Дарси-Вейсбаха:

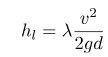
- потери давления по длине;

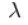
- коэффициент гидравлического сопротивления;

v – скорость движения рабочей среды;

g – ускорение силы тяжести;

d – диаметр трубопроводной магистрали.

Практически определено, что на коэффициент гидравлического сопротивления непосредственное влияние оказывает число Рейнольдса (Re) – безмерная величина, которая характеризует поток жидкости и выражается отношением динамического давления к касательному напряжению.

Если Re меньше, чем 2300, то для расчёта применяется формула:

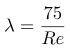
Для трубопроводов в форме круглого цилиндра:

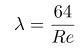
Для трубопроводных коммуникаций с другим (не круглым) сечением:

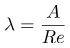
Где А=57 – для квадратных труб.

Турбулентное течение рабочего потока

При турбулентном (неравномерном, беспорядочном) перемещении рабочего потока коэффициент сопротивления вычисляют опытным путём, как функцию от Re. Если необходимо определить коэффициент гидравлического сопротивления для магистрали круглого сечения с гладкими поверхностями при

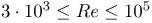
, то для расчёта применяется формула Блаузиуса:

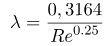
В случае турбулентного перемещения рабочей среды на величину коэффициента трения влияет число Рейнольдса (характер течения) и насколько гладкая внутренняя поверхность трубопроводной коммуникации.

Коэффициент местного сопротивления

Это безмерная величина, которая устанавливается экспериментальным путём с помощью формулы:

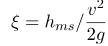
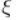
– коэффициент местного сопротивления;

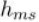
– потеря напора;

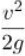
– отношение скорости потока к ускорению силы тяжести – скоростной поток.

При неизменной скорости перемещения рабочей среды по всему сечению применяется формула:

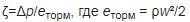
, где

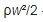
– энергия торможения.

Коэффициент гидравлического сопротивления различных труб

Для фитингов из ППР:

Деталь	Примечание	Коэффициент
Муфта	0,25
Муфта переходная	Уменьшение на 1 размер	0,40
	Уменьшение на 2 размер	0,50
	Уменьшение на 3 размер	0,60
	Уменьшение на 4 размер	0,70
Угольник 90°	1,20
Угольник 45°	0,50
Тройник	Разделение потока	1,20
Тройник	Соединение потока	0,80
Крестовина	Соединение потока	2,10
Крестовина	Разделение потока	3,70
Муфта комб. вн. рез.	0,50
Муфта комб. нар. рез	0,70
Угольник комб. вн. рез.	1,40
Угольник комб. нар. рез.	1,60
Тройник комб. вн. рез.	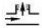1,40 - 1,80
Вентиль	20 мм	9,50
	25 мм	8,50
	32 мм	7,60
	40 мм	5,70

Для полиэтиленовых труб

Труба	Расход, м3/час	Скорость, м/с	Потери напора в метрах, на 100 метров прямого трубопровода (м/100м)
Сталь новая 133x5	60	1,4	3,6
Сталь старая 133x5	60	1,4	6,84
ПЭ 100 110x6,6 (5ЭР 17)/td>	60	2,26	4,1
ПЭ 80 110x8,1 (ЗйР 13,6)	60	2,41	4,8
Сталь новая 245x6	400	2,6	4,3
Сталь старая 245x6	400	2,6	7,0
ПЭ 100 225x13,4 (50 В 17)	400	3,6	4,0
ПЭ 80 225x16,6 (ЗЭК 13,6)	400	3,85	4,8
Сталь новая 630x10	3000	2,85	1,33
Сталь старая 630x10	3000	2,85	1,98
ПЭ 100 560x33,2 (ЗЭК 17)	3000	4,35	1,96
ПЭ 80 560x41,2 (ЗЭК 13,6)	3000	4,65	2,3
Сталь новая 820x12	4000	2,23	0,6
Сталь старая 820x12	4000	2,23	0,87
ПЭ100 800x47,4 (ЗЭК 17)	4000	2,85	0,59
ПЭ 80 800x58,8 (ЗЭР 13,6)	4000	3,0	0,69

Для бесшовных стальных труб

Режим движения		Определения λ
Ламинарный		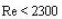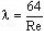или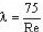
Переходный		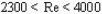Проектирование трубопроводов не рекомендуется
Турбулентный	1-я область	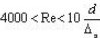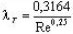(ф-ла Блазиуса) 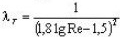Бф-ла Конакова)
	2-я область	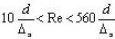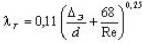(ф-ла Альтшуля)
	3-я область	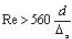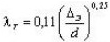(ф-ла Альтшуля) 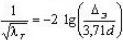(ф-ла Никурадзе)

Для металлопластиковых труб

Наименование	Символ	Коэффициент
Тройник разделения потока		7,6
Тройник проходной		4,2
Тройник противоположные потоки при разделении потока		8,5
Тройник противоположные потоки при слиянии потока		8,5
Угол 90°		6,3
Дуга		0,9
Редукционный переход		6,3
Установочный уголок		5,4

Трубы с низким коэффициентом гидравлического сопротивления

С точки зрения гидравлического сопротивления, наиболее оптимальными являются трубопроводные системы с гладкой внутренней стенкой:

Читайте также: