Тело находящееся в газе плавает на каком рисунке правильно изображены архимедова сила и сила тяжести

Обновлено: 08.01.2025

Нет времени уже во всем разбираться, но очень нужно сдать домашку
Спасибо
1. При каком условии тело, находящееся в жидкости, тонет; плавает? всплывает? 2. Как показать на опыте, что вес жидкости, вытесненной плавающим телом, равен весу тела в воздухе? 3. Чему равна выталкивающая сила, которая действует на тело, плавающее на поверхности жидкости? 4. Как зависит глубина погружения в жидкость плавающего тела от его плотности? 5. Почему водные животные не нуждаются в прочных скелетах? в. Какую роль играет плавательный пузырь у рыб? 7. Как регулируют глубину погружения киты?

НАВИГАЦИЯ ПО САЙТУ:

1.24 Закон Архимеда.

Теория: На всякое тело погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной жидкости.

Сила Архимеда возникает из за разности давлений на разных глубинах.

Сила Архимеда находится по формуле: F_А=ρgV_т

Плавание тел: В жидкости (газе) на тело действуют две силы:
F_А=ρ_жgV_т - сила Архимеда
и сила тяжести F_т=mg=ρ_тgV_т
формулы похожи, но отличие в плотностях ρ_ж и ρ_т.
Если тело находится на поверхности жидкости то силы равны F_т=F_А

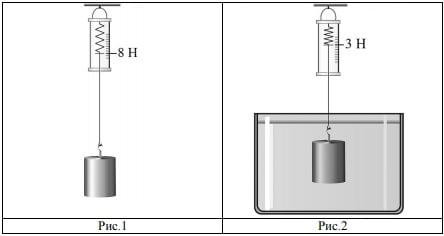
Задание демонстрационного варианта ОГЭ 2019: К динамометру прикрепили цилиндр, как показано на рисунке 1. Затем цилиндр полностью погрузили в воду (рисунок 2).

Определите объём цилиндра.
Решение: Вес цилиндра в воздухе 8 Н, в воде вес 3 Н. Следовательно, в воде на цилиндр действует выталкивающая сила (сила Архимеда) 5 Н. выталкивающая сила находится по формуле F_А=ρgV_т, нам известно что плотность воды ρ=1000 кг/(м 3 ), выразим объем цилиндра
V_т=F_А/(ρg)=5/(1000·10)=0,0005 м 3 = 500 см 3 . т.к. (1м 3 =1000000см 3 )
Ответ: 500

Задание фипи: На рычажных весах уравновешены два сплошных шара: медный и железный. Нарушится ли равновесие весов и если нарушится, то как, если шары опустить в воду? Ответ поясните.
Решение: Так как шары уравновешены на рычажных весах, следовательно их массы равны, при опускании в воду на шары начнет действовать сила Архимеда F_А=ρ_жgV_т,
m=ρV, так как плотность меди ρ_Сu=8900 кг/м 3 больше чем плотность железа ρ_Fe=7800кг/м 3 , значит объем медного шара меньше объема железного V_Сu

Персональный сайт учителя физики Германова Сергея Константиновича.
Все права защищены © 2018–

Брусок массой m погружен в жидкость и находится в равновесии.

Изображенные на рисунке сила Архимеда Fа и сила тяжести mg равны по модулю согласно.

В ответе: второму закону Ньютона. Разве не третьему? Fa = -Fт => |Fа| = |Fт|

Третий здесь ни при чем. Силы по 3-му з. Н. приложены к РАЗНЫМ телам. А нас интересует одно тело - брусок. Раз он находится в равновесии (не ускоряется) , значит, равнодействующая сил равна нулю.

Закон Архимеда — закон статики жидкостей и газов, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа) и направленная по вертикали вверх.

Ниже приведены выводы, следующие из закона Архимеда.

Действие жидкости и газа на погруженное в них тело .

Если погрузить в воду мячик, наполненный воздухом, и отпустить его, то он всплывет. То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?

На тело, погруженное в воду, со всех сторон действуют силы давления воды (рис. а). В каждой точке тела эти силы направлены перпендикулярно его поверхности. Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростатическое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих иа тело сверху.

Если заменить все силы давления, приложенные к погруженному в воду телу, одной (результирующей или равнодействующей) силой, оказывающей на тело то же самое действие, что и все эти отдельные силы вместе, то результирующая сила будет направлена вверх. Это и заставляет тело всплывать. Эта сила называется выталкивающей силой, или архимедовой силой (по имени Архимеда, который впервые указал на ее существование и установил, от чего она зависит). На рисунке б она обозначена как F_A.

Архимедова (выталкивающая) сила действует на тело не только в воде, но и в любой другой жидкости, т. к. в любой жидкости существует гидростатическое давление, разное на разных глубинах. Эта сила действует и в газах, благодаря чему летают воздушные шары и дирижабли.

Благодаря выталкивающей силе вес любого тела, находящегося в воде (или в любой другой жидкости), оказывается меньше, чем в воздухе, а в воздухе меньше, чем в безвоздушном пространстве. В этом легко убедиться, взвесив гирю с помощью учебного пружинного динамометра сначала в воздухе, а затем опустив ее в сосуд с водой.

Уменьшение веса происходит и при переносе тела из вакуума в воздух (или какой-либо другой газ).

Если вес тела в вакууме (например, в сосуде, из которого откачан воздух) равен P₀, то его вес в воздухе равен:

где F´_A — архимедова сила, действующая на данное тело в воздухе. Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что P_возд.=P₀=mg.

Вес тела в жидкости уменьшается значительно сильнее, чем в воздухе. Если вес тела в воздухе P_возд.=P₀, то вес тела в жидкости равен P_жидк = Р₀ — F_A. Здесь F_A — архимедова сила, действующая в жидкости. Отсюда следует, что

Поэтому чтобы найти архимедову силу, действующую на тело в какой-либо жидкости, нужно это тело взвесить в воздухе и в жидкости. Разность полученных значений и будет архимедовой (выталкивающей) силой.

Другими словами, учитывая формулу (1.32), можно сказать:

Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.

Определить архимедову силу можно также теоретически. Для этого предположим, что тело, погруженное в жидкость, состоит из той же жидкости, в которую оно погружено. Мы имеем право это предположить, так как силы давления, действующие на тело, погруженное в жидкость, не зависят от вещества, из которого оно сделано. Тогда приложенная к такому телу архимедова сила F_A будет уравновешена действующей вниз силой тяжести m_жg (где m_ж — масса жидкости в объеме данного тела):

Но сила тяжести равна весу вытесненной жидкости Р_ж. Таким образом.

Учитывая, что масса жидкости равна произведению ее плотности ρ_ж на объем, формулу (1.33) можно записать в виде:

где V_ж — объем вытесненной жидкости. Этот объем равен объему той части тела, которая погружена в жидкость. Если тело погружено в жидкость целиком, то он совпадает с объемом V всего тела; если же тело погружено в жидкость частично, то объем V_ж вытесненной жидкости меньше объема V тела (рис. 1.39).

Формула (1.33) справедлива и для архимедовой силы, действующей в газе. Только в этом случае в нее следует подставлять плотность газа и объем вытесненного газа, а не жидкости.

С учетом вышеизложенного закон Архимеда можно сформулировать так:

На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или газа), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).

Продолжаем подготовку к олимпиадам. Тема сегодняшней статьи – сила Архимеда. Рекомендую начать с предыдущей статьи, там представлены более простые, вводные, задачи. Здесь немного сложнее, но тоже уровня городской олимпиады, не более.

Задача 1. Шар лежит на дне сосуда, погруженный в воду на 1/2 своего объема и давит на дно сосуда с силой равной 1/5 от действующей на шар силы тяжести. Найти плотность материала шара , если плотность воды равна .

На шар действуют силы:

$N=\frac<1> По условию mg$
, поэтому

$\frac V \rho_0 g+\fracmg=mg$

$\frac<1> V \rho_0=\fracV\rho$

$\rho=\frac \rho_0=\frac\cdot1000=625$

Ответ: 625 кг/м .

Задача 2. Тело плавает на границе двух несмешивающихся жидкостей с плотностями и (). При этом отношение объемов, погруженных в нижнюю и верхнюю жидкости, равно =n" width="54" height="22" />
. Определите плотность тела.

Запишем условие плавания:

Масса тела может быть записана как

Сила Архимеда сложится из двух слагаемых: сил Архимеда, действующих на каждый из объемов:

$(V_1+V_2)\rho_t g=\rho_1 g V_1+\rho_2 g V_2$

$\rho_t=\frac<\rho_1 V_1+\rho_2 V_2> < V_1+V_2>=\frac< nV_2+V_2>=\frac< n+1>$

$\rho_t=\frac<\rho_1 n+\rho_2> Ответ: < n+1>$
.

Задача 3. К коромыслу весов подвешены два груза равной массы. Если один из грузов поместить в жидкость плотности " width="22" height="12" />
, а другой в жидкость плотности " width="23" height="12" />
, то равновесие сохраняется. Найдите отношение плотностей грузов.

Сила, действующая на груз, погруженный в жидкость, равна разности его веса и силы Архимеда:

$F=mg-F_A=\rho V g-\rho_0 V g$

Пусть плотность одного груза , а второго – . Так как у грузов равные массы, то очевидно, что плечи рычага равны. Обозначим длину рычага , плечи сил тогда будут иметь длину . Тогда:

$L(\rho_1 V_1 g-\rho_<01 > V_1 g)=L(\rho_2 V_2 g-\rho_ V_2 g)$

$V_1(\rho_1-\rho_<01 > )= V_2(\rho_2-\rho_)$

Но , , или

$\frac<V_1> =\frac$

$\frac <\rho_1-\rho_<01 > >= \frac>$

$1-\frac <\rho_<01 > >=1-\frac>$

$\frac<\rho_1 > =\frac >>$

Задача 4. Определите силу натяжения нижней лески у поплавка, изображенного на рисунке, если поплавок погружен в воду на две трети своей длины. Масса поплавка 2 г.

Здесь нужно аккуратно расставить силы, действующие на поплавок. Сила тяжести приложена к центру масс тела, а вот сила Архимеда – к центру погруженного объема. Поэтому рисунок такой:

Определяем плечи сил относительно точки приложения силы Архимеда: у силы натяжения нижней лески плечо – проеция на горизонтальную ось " width="7" height="22" />
длины поплавка, а у силы – (проекция на горизонтальную ось " width="7" height="22" />
длины поплавка).

$T=\frac<mg> =0,01$

Задача 5. Подводная опора, забитая в глинистый грунт водоема глубиной м, представляет из себя два соосных цилиндра различного диаметра. Найти силу, действующую на опору со стороны воды в водоеме, если площадь сечения цилиндра меньшего диаметра, забитого в грунт, равна м , объем части опоры, находящейся в воде, м , плотность воды 1 г/см .

Пусть площадь верхнего основания , площадь нижнего – . Тогда площадь “шляпки” . Выталкивающая сила, действующая на “шляпку” снизу, равна

$\[F$

Сила, прижимающая опору сверху:

$\[F$

результирующая будет равна

$\[F$

В составе этой результирующей сила Архимеда

$F_A=\rho_0 g(h_2S_2-h_1S_1)=\rho_0 gh_2S_2-\rho_0 gh_1S_1=F_2-F_1$

А два последних слагаемых – это сила, показанная на рисунке как

$\[F$

Ответ: в нашем случае сила прижимает сваю ко дну (поэтому в ответе минус), Н.

Читайте также: