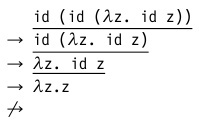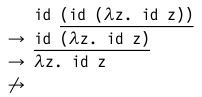Q лямбда m что за формула

Под плавлением в физике подразумевают процесс превращения тела из твердого состояния в жидкое, под действием температуры. Классическим повсеместным примером плавления из жизни является таяние льдов, их превращение в воду, или превращение твердого куска олова в жидкий припой под действием паяльника. Передача тому или иному телу определенного количества тепла может изменить его агрегатное состояние, это удивительное свойство твердых тел превращаться в жидкие под действием температуры имеет большое значение для науки и техники. Ученым (а также техникам, инженерам) важно знать при каких температурах плавятся те или иные металлы (а порой и не только металлы), и для этого в физику вошло такое понятие как «удельная теплота плавления». О том, что означает удельная теплота плавления, какая ее формула расчета, читайте далее.
Почему твердое тело становится жидким?
Но давайте для начала разберем, как происходит сам процесс плавления на атомно-молекулярном уровне. Как мы знаем, в любом твердом теле все атомы и молекулы находятся четко и упорядочено в узлах кристаллической решетки, благодаря этому твердое тело и является твердым.
Но что происходит, если мы начинает это самое гипотетическое твердо тело сильно нагревать – под действием температуры атомы и молекулы резко увеличивают свою кинетическую энергию и по достижении определенных критических значений, они начинают покидать кристаллическую решетку, вырываться из нее. А само твердое тело начинает буквально распадаться, превращаясь в некое жидкое вещество – так происходит плавление.
При этом процесс плавления происходит не резким скачком, а постепенно. Также стоит заметить, что плавление относится к эндотермическим процессам, то есть процессам, при которых происходит поглощение теплоты.
Процесс обратный к плавлению называют кристаллизацией – это когда тело из жидкого состояния наоборот превращается в твердое. Если вы оставите воду в морозилке, она через какое-то время превратится в лед – это самый типичный пример кристаллизации из реальной жизни.
Определение удельной теплоты плавления
Формула удельной теплоты плавление выглядит так:
Где m – масса плавящегося вещества, а Q – количество тепла, переданное веществу при плавлении.
Зная значение удельной теплоты плавления, мы можем определить, какое количество тепла необходимо передать для тела с той или иной массой, для его полного расплавления:
Для разных веществ удельная теплота плавления была определена экспериментально.
Единица удельной теплоты плавления
Многих интересует вопрос, в каких единицах измеряется удельная теплота плавления. Так вот, удельная теплота плавления измеряется в Джоулях на килограмм – Дж/кг.
Таблица удельной теплоты плавления
Значение удельной теплоты для разных веществ: золота, серебра, цинка, олова и многих других металлов можно найти в специальных таблицах и справочниках. Обычно эти значения приводятся в виде таблицы.
Вашему вниманию таблица удельной теплоты плавления разных веществ
| Вещество | 10 5 * Дж/кг | ккал/кг | Вещество | 10 5 * Дж/кг | ккал/кг |
| Алюминий | 3,8 | 92 | Ртуть | 0,1 | 3,0 |
| Железо | 2,7 | 65 | Свинец | 0,3 | 6,0 |
| Лед | 3,3 | 80 | Серебро | 0,87 | 21 |
| Медь | 1,8 | 42 | Сталь | 0,8 | 20 |
| Нафталин | 1,5 | 36 | Цинк | 1,2 | 28 |
| Олово | 0,58 | 14 | Платина | 1,01 | 24,1 |
| Парафин | 1,5 | 35 | Золото | 0,66 | 15,8 |
Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.
Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.
Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…
λ-исчисление: основные понятия
Синтаксис
В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.
Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.
Термы:
| переменная: | x |
| лямбда-абстракция (анонимная функция): | λx.t , где x — аргумент функции, t — её тело. |
| применение функции (аппликация): | f x , где f — функция, x — подставляемое в неё значение аргумента |
- Применение функции левоассоциативно. Т.е. s t u — это тоже самое, что (s t) u
- Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е. λx. λy. x y x означает то же самое, что λx. (λy. ((x y) x))
- Скобки явно указывают группировку действий.
Может показаться, будто нам нужны какие-то специальные механизмы для функций с несколькими аргументами, но на самом деле это не так. Действительно, в мире чистого лямбда-исчисления возвращаемое функцией значение тоже может быть функцией. Следовательно, мы можем применить первоначальную функцию только к одному её аргументу, «заморозив» прочие. В результате получим новую функцию от «хвоста» аргументов, к которой применим предыдущее рассуждение. Такая операция называется каррированием (в честь того самого Хаскелла Карри). Выглядеть это будет примерно так:
| f = λx.λy.t | Функция с двумя аргументами x и y и телом t |
| f v w | Подставляем в f значения v и w |
| (f v) w | Эта запись аналогична предыдущей, но скобки явно указывают на последовательность подстановки |
| ((λy.[x → v]t) w) | Подставили v вместо x . [x → v]t означает «тело t , в котором все вхождения x заменены на v » |
| [y → w][x → v]t | Подставили w вместо y . Преобразование закончено. |
И напоследок несколько слов об области видимости. Переменная x называется связанной, если она находится в теле t λ-абстракции λx.t . Если же x не связана какой-либо вышележащей абстракцией, то её называют свободной. Например, вхождения x в x y и λy.x y свободны, а вхождения x в λx.x и λz.λx.λy.x(y z) связаны. В (λx.x)x первое вхождение x связано, а второе свободно. Если все переменные в терме связаны, то его называют замкнутым, или комбинатором. Мы с вами будем использовать следующий простейший комбинатор (функцию тождества): id = λx.x . Она не выполняет никаких действий, а просто возвращает без изменений свой аргумент.
Процесс вычисления
Рассмотрим следующий терм-применение:
Его левая часть — (λx.t) — это функция с одним аргументом x и телом t . Каждый шаг вычисления будет заключаться в замене всех вхождений переменной x внутри t на y . Терм-применение такого вида носит имя редекса (от reducible expression, redex — «сокращаемое выражение»), а операция переписывания редекса в соответствии с указанным правилом называется бета-редукцией.
Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:
который для простоты можно переписать как
(напомним, что id — это функция тождества вида λx.x )
В этом терме содержится три редекса: 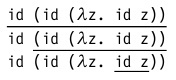
- Полная β-редукция. В этом случае каждый раз редекс внутри вычисляемого терма выбирается произвольным образом. Т.е. наш пример может быть вычислен от внутреннего редекса к внешнему:
![]()
- Нормальный порядок вычислений. Первым всегда сокращается самый левый, самый внешний редекс.
![]()
- Вызов по имени. Порядок вычислений в этой стратегии аналогичен предыдущей, но к нему добавляется запрет на проведение сокращений внутри абстракции. Т.е. в нашем примере мы останавливаемся на предпоследнем шаге:
![]()
Оптимизированная версия такой стратегии (вызов по необходимости) используется Haskell. Это так называемые «ленивые» вычисления. - Вызов по значению. Здесь сокращение начинается с самого левого (внешнего) редекса, у которого в правой части стоит значение — замкнутый терм, который нельзя вычислить далее.
![]()
Для чистого лямбда-исчисления таким термом будет λ-абстракция (функция), а в более богатых исчислениях это могут быть константы, строки, списки и т.п. Данная стратегия используется в большинстве языков программирования, когда сначала вычисляются все аргументы, а затем все вместе подставляются в функцию.
Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение
(λx.λy. x) z ((λx.x x)(λx.x x))
Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.
Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y . Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y , а z — первоначальный терм имел бы вид (λx.λz.x)y и после редукции выглядел бы как λz.y . Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.
Так же бывает, что у нас есть абстракция λx.t x , причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t . Такое преобразование называется η-конверсией.
На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.
Дифракционная решетка - оптическое устройство, представляющее собой совокупность большого числа параллельных щелей, равноудаленных друг от друга.
Суммарная ширина щели и штриха (a+b=d) – период решетки.
! d=((a+b)*N)/N=C/N!, где С –ширина решетки, N -число штрихов на ней.

на нем: Л- линза; Р – решетка; Э - экран
Максимумы, которые образуются на экране, после интерференции вторичных волн, идущих от узких щелей, удовлетворяют условию:
!d*sin фи = k*лямбда! - формула дифракционной решетки.
фи - угол дифракции (угол отклонения от прямолинейного направления);
k - порядок спектра;
лямбда - длина волны света, освещающего решетку,
Дифракционные спектры для монохроматического света представляет собой чередование максимумов и минимумов по обе стороны от центрального механизма. Максимумы имеют цвет соответствующей длины света, освещающего решетку.
Если решетку освещать белым светом, то центральный максимум будет белым, а остальные будут представлять собой чередование цветных полос плавно переходящих друг в друга, т. к. sin фи= k*лямбда/d - зависит от длины волны света. D = к/t - угловая дисперсия решетки. R =k*N - разрешающая способность.
Диффузия в жидкости. Уравнение Фика. Уравнение диффузии для мембран.
Диффузия - самопроизвольное проникновение молекул одного вещества между молекулами других.
Явление диффузии - важный элемент диффракционирования мембран. При диффузии происходит перенос массы вещества. В биофизике это называется транспорт частиц. Основным уравнением диффузии является уравнение Фика:
где I – плотность частиц при диффузии в жидкость.
D – коэффициент диффузии.
Коэффициент 1/3 возник ввиду трехмерного пространства и хаоса в движении молекул (в среднем в каждом из 3-х направлений перемещается 1/3 часть всех молекул)
сигма - средняя длина свободного пробега молекул
тау -среднее время оседлой жизни молекул
С- массовая концентрация молекул
Х- перемещение молекул вдоль оси X
- градиент массовой концентрации
Знак «-» показывает, что диффузия молекул происходит из области их большей концентрации в область меньшей концентрации.
Уравнение диффузии можно записать в виде:
n – концентрация молекул.
Градиент концентрации
R- универсальная газовая постоянная; Т- абсолютная температура градиент химического потенциала,
Тогда
С - концентрация частиц. А Эйнштейн показал, что D пропорционально Т. Дня биологических мембран уравнение Фика имеет вид:
- концентрация молекул внутри клеток
- коэффициент проницаемости
l – толщина мембраны.
Дифракция света на щелях.
Дифракцией света называют явление отклонения света от прямолинейного распространения в среде с резкими неоднородностями.
Описать картину дифракции можно с учетом интерференции вторичных волн.

Рассмотрим дифракцию от узкой щели (АВ)
MN – непрозрачная преграда;
АВ=а – ширина щели;
АВ – часть волновой поверхности, каждая точка которой является источником вторичных волн, которые распространяются за щелью по разным направлениям. Линза соберет лучи А, А1 и В в точке О1 экрана.
АD - перпендикуляр к направлению пучка вторичных волн. Разбили ВD на отрезки =лямда/2.
АА1, А1В - зоны Френеля. Вторичные волны, идущие от двух соседних зон Френеля, не гасят друг друга, так как отличаются по фазе на пи. Число зон, укладывающихся в щели, зависит от длины волны лямда и угла альфа.
Поэтому на экране получится система светлых (mах) и темных (min) полос симметричных относительно центра (альфа=треугольник - изменение) - наиболее яркой полосы.
Интенсивность остальных максимумов убывает с увеличением к.
3аконы излучения абсолютно чёрного тела (Стефана - Больцмана, Вина). Формула Планка. Использование термографии в диагностике.
Излучение чёрного тела имеет сплошной спектр. Графически это выглядит для разных температур так:
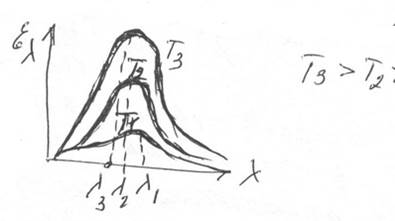
Существует максимум спектральной светимости, который при повышении
температуры смещается в сторону коротких волн.
По мере нагревания чёрного тела его энергетическая светимость (Re)
увеличивается: Re = опред интеграл от 0 до бескон от Eлямда*dлямда
Стефан и Больцман установили, что Re=сигма*T^4
Сигма = 5,6696*10^-8 Вт/K*м^2 - постоянная Стефана-Больцмана,
T=t+273 - абсолютная (термодинамическая) температура по шкале
Кельвина. Все замечали это на практике, чем выше температура спирали, нагретой печи, тем больше они излучают тепла.

Планк получил формулу для спектральной плотности абсолютно черного тела (Eлямда) и серого тела (r лямда) (лямда-индекс): Eлямда=2п*h*c^2/лямда^5 * 1/exp[h*c/k*T*лямда-1]
альфа - коэффициент поглощения
h - постоянная Планка;
С - скорость света в вакууме;
лямда - длина волны;
k - постоянная Больцмана;
Т - абсолютная температура.
2 Затухающие колебания и декремент затухания. Апериодические колебания.
Свободные колебания (происходящие без внешнего воздействия периодически действующей силы) являются затухающими. График затухающих колебаний имеет вид:

Амплитуда колебаний с каждым разом убывает. Затуханию способствуют силы трения и сопротивления, возникающие в средах. Пусть r-коэффициент трения, характеризующий свойство среды оказывать сопротивление движению. Тогда БЕТТА= r/2m – коэффицент затухания.
Wo= корень(K/m) – циклическая частота собственных колебаний, тогда W^2=Wo^2-БЕТТА^2, где W – циклическая частота затухания колебаний.
Быстрота затухания колебаний определяется коэффициентом затухания. Уравнение затухающих колебаний имеет вид А=Ао*l в степени минус бета*t
Ao – первоначальная амплитуда, А-амплитуда затухающих через время t.
Лямда=lnA(t)/A(t+T)=lnAo*(e в степени минус бета*t)/Ao*e^-бета*(t+T)=ln(e^ бета*t) –логарифмический декрет затухания.
!Лямда=бета*Т!- связь логарифмического декремента затухания с коэффициентом затухания. При сильно затухании колебания становятся апериодическими (если бета^2>Wo^2)
№31 Импеданс полной цепи переменного тока. Сдвиг фаз. Резонанс напряжения.
Рассмотрим последовательно соединенные R, L, C.
При последовательном соединении:

1) Uвх=U0*cosW*t=Ur+Ul+Uc – входное напряжение.
2) I=I0*cos(W*t-фи) – сила тока в цепи.
Начертим векторную диаграмму:

Ur0 – совпадает по фазе с силой тока;
Ul0 – опережает на пи/2;
Uc0 – отстает от тока на пи/2.
По теореме Пифагора: (U0)^2=(U0r)^2+(U0l-U0c)^2
Сократив обе части уравнения на (I0)^2 получим выражение для полного сопротивления (Z):
Z=квадратный корень из (R^2+(W*L-1/W*c)^2) – импеданс.
Если сопротивление катушки Xl= W*L равно сопротивлению конденсатора Xc=1/W*c, то полное сопротивление Z=R; по закону Ома Iрез=U0/Z=U0/R (Iрез – резонансный ток) – сила тока резко возрастает – РЕЗОНАНС. При этом Ul=Uc>>U0 – резонанс напряжений. Это возможно, т.к. Ul и Uc сдвинуты по фазе между собой на пи:

При этом на резисторе R выделяется максимальное количество теплоты:
№32 Импенданс тканей организма. Эквивалентная Электрическая схема. Оценка жизнеспособности тканей и органов но частотной зависимости к углу сдвига фаз.
Ткани организма проводят как постоянный так и переменный ток. Биологическая мембрана а значит и весь организм обладает емкостным сопротивлением, т.к. обладают емкостью, т.е. способны
накапливать заряд. При пропускании через живые ткани переменного тока наблюдается отставание напряжения от тока. Омические емкостные свойства биологических тканей можно моделировать используя эквивалентные электрические схемы, при любых частотах зависимость сдвига фаз и импенданса от частоты выполняется для схемы
1/Zв2=1/Rв2+1/корень(R1 в2+1/Wв2*Св2)!, где Z-полное сопротивление данной цепи, с - ёмкость.
При малых частотах: Z=R2 При больших частотах: Zmin=(R1*R2)/(R1+R2).

Графическое изображение зависимости импенданса живой ткани от частоты переменного тока.
Сдвиг фаз между током и напряжением tg фи = R/Xc=RWC (1).

Частотная зависимость сдвига фаз живой ткани. При отмирании ткани натрий-калиевый канал биологических мембран разрушается, цитоплазма
клетки (проводник) соединяется с межклеточной
жидкостью(проводник) и емкостные свойства ткани уменьшаются, а это значит, что и импенданс (Z) и сдвиг фаз (фи) меньше зависят от частоты. Мёртвая ткань обладает лишь омическим сопротивлением (R), и не зависит от частоты. Диагностический метод, основанный на регистрации изменения импенданса тканей и сдвига фаз называется РЕОГРАФИЕЙ.
Сомнительная заправка, плохой бензин, «чек» на панели — стандартный и быстрый путь к замене кислородного датчика. Про лямбда-зонд слышали многие автомобилисты, но мало кто разбирался, за что именно он отвечает и почему так легко выходит из строя. Рассказываем про датчик кислорода — «обоняние» двигателя.
Лямбда и стехиометрия двигателя
Название датчика происходит от греческой буквы λ (лямбда), которая обозначает коэффициент избытка воздуха в топливно-воздушной смеси. Для полного сгорания смеси соотношение воздуха с топливом должно быть 14,7:1 (λ=1). Такой состав топливно-воздушной смеси называют стехиометрическим — идеальным с точки зрения химической реакции: топливо и кислород в воздухе будут полностью израсходованы в процессе горения. При этом двигатель произведёт минимум токсичных выбросов, а соотношение мощности и расхода топлива будет оптимальным.
Если лямбда будет <1 (недостаток воздуха), смесь станет обогащённой; при лямбде >1 (избыток воздуха) смесь называют обеднённой. Чересчур богатая смесь — это повышенный расход топлива и более токсичный выхлоп, а слишком бедная смесь грозит потерей мощности и нестабильной работой двигателя.
Из графика видно, что при λ=1 мощность двигателя не пиковая, а расход топлива не минимален — это лишь оптимальный баланс между ними. Наибольшую мощность мотор развивает на слегка обогащённой смеси, но расход топлива при этом возрастает. А максимальная топливная эффективность достигается на слегка обеднённой смеси, но ценой падения мощности. Поэтому задача ЭБУ (электронного блока управления) двигателя — корректировать топливно-воздушную смесь исходя из ситуации: обогащать её при холодном пуске или резком ускорении, и обеднять при равномерном движении, добиваясь оптимальной работы мотора во всех режимах. Для этого блок управления ориентируется на показания датчика кислорода.
Зачем нужен кислородный датчик
Датчиков в современном двигателе великое множество . С помощью различных сенсоров ЭБУ замеряет температуру забортного воздуха и его поток, «видит» положение дроссельной заслонки, отслеживает детонацию и положение коленвала — словом, внимательно следит за воздухом «на входе» и показателями работы мотора, регулируя подачу топлива для создания оптимальной смеси в цилиндрах.
Лямбда-зонд показывает, что же получилось «на выходе», замеряя количество кислорода в выхлопных газах. Другими словами, кислородный датчик определяет, оптимально ли работает мотор, соответствуют ли расчёты ЭБУ реальной картине и нужно ли вносить в них поправки. Основываясь на данных с лямбда-зонда, ЭБУ вносит соответствующие коррекции в работу двигателя и подготовку топливно-воздушной смеси.
Где находится кислородный датчик
Датчик кислорода установлен в выпускном коллекторе или приёмной трубе глушителя двигателя, замеряя, сколько несгоревшего кислорода находится в выхлопных газах. На многих автомобилях есть ещё один лямбда-зонд, расположенный после каталитического нейтрализатора выхлопа — для контроля его работы.
Если у двигателя две головки блока (V-образники, «оппозитники»), то удваивается количество выпускных коллекторов и катализаторов, а значит и лямбда-зондов — у современной машины может быть и 4 кислородных датчика.
Устройство кислородного датчика
Классический лямбда-зонд порогового типа — узкополосный — работает по принципу гальванического элемента. Внутри него находится твёрдый электролит — керамика из диоксида циркония, поэтому такие датчики часто называют циркониевыми. Поверх керамики напылены токопроводящие пористые электроды из платины. Будучи погружённым в выхлопные газы, датчик реагирует на разницу между уровнем кислорода в них и в атмосферном воздухе, вырабатывая на выходе напряжение, которое считывает ЭБУ.
Циркониевый элемент лямбда-зонда приобретает проводимость и начинает работать только после прогрева до температуры 300 °C. До этого ЭБУ двигателя действует «вслепую» согласно топливной карте, без обратной связи от кислородного датчика, что повышает расход топлива при прогреве двигателя и количество вредных выбросов. Чтобы быстрее задействовать лямбда-зонд, ему добавляют принудительный электрический подогрев. Кислородные датчики с подогревом внешне отличаются увеличенным количеством проводов: у них 3–4 жилы против 1–2 у обычных датчиков.
В названии узкополосного датчика кроется его недостаток — он способен замерять количество кислорода в выхлопе в достаточно узком диапазоне. ЭБУ может корректировать смесь по его показаниям только в некоторых режимах работы мотора (холостой ход, движение с постоянной скоростью), что не отвечает современным требованиям по экономичности и экологичности двигателей. Для более точных замеров в широком диапазоне используют широкополосный лямбда-зонд (A/F-сенсор), который также называют датчиком соотношения «воздух-топливо» (Air/Fuel Sensor). Обычно к нему подходят 5–6 проводов, хотя бывают и исключения.
Внешне «широкополосник» похож на обычный датчик кислорода, но внутри есть отличия. Благодаря специальным накачивающим ячейкам эталонный лямбда-коэффициент газового содержимого датчика всегда равен 1, и генерируемое им напряжение постоянно. А вот ток меняется в зависимости от количества кислорода в выхлопных газах, и ЭБУ двигателя считывает его в реальном времени. Это позволяет электронике быстрее и точнее корректировать смесь, добиваясь её полного сгорания в цилиндрах.
Почему до сих пор производят узкополосные датчики? Во-первых, для старых автомобилей, где A/F-сенсоры не применялись. Во-вторых, из-за особенностей «широкополосника» его нельзя устанавливать после катализатора, где он быстро выходит из строя. А контролировать работу катализатора как-то надо. Поэтому в современных двигателях ставят два лямбда-зонда разного типа: широкополосный (управляющий) — в районе выпускного коллектора, а узкополосный (диагностический) — после катализатора.
Причины и признаки неисправности лямбда-зонда
Основная причина поломок кислородных датчиков — некачественный бензин: свинец и ферроценовые присадки оседают на чувствительном элементе датчика, выводя его из строя. На состояние лямбда-зонда влияет и нестабильная работа двигателя: при пропусках зажигания от старых свечей или пробитых катушек несгоревшая смесь попадает в выхлопную систему, где догорает, выжигая и катализатор, и датчики кислорода. Приговорить датчик также может попадание в цилиндры антифриза или масла.
Самый очевидный признак неисправности лямбда-зонда — индикатор Check Engine на приборной панели. Считав код ошибки с помощью сканера или самодиагностики, можно проверить, какой именно датчик вышел из строя, если их несколько. Иногда всё дело в повреждённой проводке датчика — с проверки цепи и стоит начать поиск поломки.
Но далеко не всегда проблемный лямбда-зонд зажигает «Чек»: иногда он не ломается полностью, а медленно умирает, давая при этом ложные показания, из-за чего ЭБУ двигателя неверно корректирует состав смеси. В этом случае нужно ориентироваться на косвенные признаки — ухудшение работы двигателя.
Проблемы с датчиком кислорода нарушают всю систему обратной связи и лямбда-коррекции, вызывая целый букет неисправностей. Прежде всего, это увеличение расхода топлива и токсичности выхлопа, снижение мощности и нестабильный холостой ход. Если вовремя не заменить лямбда-зонд, следом выйдет из строя каталитический нейтрализатор, осыпавшись из-за перегрева от обогащённой смеси.
Универсальные кислородные датчики
Цена на оригинальные датчики кислорода вряд ли обрадует автомобилистов, но все лямбда-зонды работают по единому принципу, что позволяет без труда подобрать замену. Главное, чтобы соответствовал типа датчика (широкополосный/узкополосный), количество проводов и резьбовая часть. В продаже есть универсальные кислородные датчики без разъёма, которые можно использовать на десятках моделей автомобилей — подобрать и купить лямбда-зонд не составляет проблемы.
Чтобы избежать проблем с кислородными датчиками, следите за состоянием двигателя, заправляйтесь качественным топливом и регулярно выполняйте компьютерную диагностику, которая позволит выявить неисправности на ранней стадии.
Важно совершенствовать математику.
Внимание! Данное сообщение содержит исключительно личное мнение автора. Есть основания полагать, что оно может не отвечать критериям научности.
| Цитата |
|---|
| Алексей Трофимов пишет: То есть, могут возникать и более тяжелые частицы с "центрами центров", но только в результате самых грандиозных катастроф, преобразующих ГА соответствующего уровня модуляции, в супертяжелые частицы. |
Важно совершенствовать математику.
Внимание! Данное сообщение содержит исключительно личное мнение автора. Есть основания полагать, что оно может не отвечать критериям научности.
| Цитата |
|---|
| Петр Тайгер пишет: Наверное, в недалеком будущем, уже после БАК-а, произойдет следующее - в областях ультравысоких энергий (что априори - и в областях ультрамалых пространственно-временных масштабов) приведет кроманьонов к выводу о том, что само понятие частицы в этих областях станет несостоятельным, - энергия, связанная с взаимодействием, окажется намного больше энергии, соответствующей массе покоя частицы, и вся процедура вторичного квантования, которой обязано появление частицы в нынешней теории поля, - коту под хвост, - сплошное противоречие, - однако! |
Важно совершенствовать математику.
Внимание! Данное сообщение содержит исключительно личное мнение автора. Есть основания полагать, что оно может не отвечать критериям научности.
[QUOTE]Алексей Трофимов пишет:
Рассматривая приведенную формулу лямбда = h/mc можно заметить, что это по сути соотношение неопреденностей Гейзенберга дельта х *дельта p = h так как mc это импульс. Тем более "странно", почему никто не замечает, что из этого ракурса следует - размер электрона равен половине среднего размера атома и , следовательно, ни о какой планетарной
вать внутри формул символами и пока не обращая внимание на Вашу ключевую фразу « примем во внимание следствие ГР о том, что масса и длина волны жестко связаны, (неизбежный структурализм ГР), то это позволит записать произведение
например, через M и следовательно формула приобретет вид M*c = h ».
Мне особенно нравится вот это волшебное превращение из
« лямбда х m х С »
в
и потому, мол, вот как все просто –
и, ясен пень, С никак не может быть константой, и сей факт, конечно же, ставит под сомнение всю сегодняшнюю физику как таковую. 8)
***
Хорошо. Начнем с определений, наполненных хотя бы какого-то физического смысла.
Допустим, я не знаю темы Алексея Трофимова «Математика …….гносеологии» и оттого действую, как махрово закоренелый классически-традиционный ортодокс. 8)
***
Вещество излучает или поглощает энергию квантами (порциями), пропорциональными излучаемой или поглощаемой частоте. Энергия одной порции (кванта):
Частица взаимодействует с фотонами света, облучающего частицу. Здесь существенно, что фотон, характеризируемый волновыми параметрами .является в то же время носителем определенной энергии и количества движения. Давайте даже скажем так – носите лем свойств «частицы света». Теперь смотрим. В наших рассуждениях появилась «энергия». Продолжаем дальше. Мы должны учитывать в своих дальнейших рассуждениях волновые и корпускулярные свойства фотона и как они повязаны с понятим «энергия». Это ортодоксальная классика. В одних ситуациях свет ведет себя как волна, а в других ситуациях свет ведет себя как поток частиц (фотонов).
Фотон обладает энергией
Частица с энергией Е обладает массой
C ^ - ( C в квадрате , прим. П.Тайгер ).
Фотон – частица, движущаяся со скоростью света С .
Мы знаем, что фотон - это особая частица – он может существовать только в движении со скоростью С и никогда в отличии от других частиц не имеет массы покоя.
h x частота = m x C ^
Импульс фотона p = m x C и,
p = h x частота / C ,
Эту формулу-закон, устанавливающий зависимость длины волны, связанной с движущейся частицей, от импульса частицы, как известно, и получил Луи де Бройль.
h = лямбда х m x C.
***
Почему никто еще тогда, во времена Луи ле Бройля (1924 г.) не «уплотнил» произведение лямбда * m до символа-константы M , вроде бы, тоже понятно: хотя и просматривается здесь жесткая конструкция взаимоувязки массы и длины волны, - проследим еще раз, -
Е = h x частоту , или
h x частоту = m x C ^ ,
но с какого вдруг такого перепугу здесь компоновать дуализм проявлений волны и корпускулы в нечто единое в виде какой-то странного М ?
это волновые свойства фотона в правой части уравнения, а
это фотон как частица в правой части уравнения.
Частица тогда, когда фотон приобретает массу в движении.
Движение – это импульс фотона p , равный, как и полагается
m x C .
Разделили мухи от котлет, так сказать. Дальше понятно (крутанемся белкой в колесе…) –
p = h x частота , или
Сразу же после опубликования такого рода хода рассуждений Л. де Бройля Дэвиссон и его колега Д. Джермер установили, что такие частицы, как электрон дифрагируют как волны, а длины этих волн полностью соответствуют формуле Л. Де Бройля.
И только уже отталкиваясь от этих рассуждений, Гейзенберг через три года, в 1927 году (принцип полной неопределенности импульса частицы при знании ее точной координаты, и наоборот, полной неопределенности координаты частицы при точном знании импульса частицы), установил предельную точность, с котрой можно одновременно определить координату и импульс частицы, и получил то соотношение неопределенностей, которые в самом начале одного из своих предыдущих постов приводите и Вы, Алексей:
дельта икс умножено на дельта р равно или больше h ,
где дельта х – неопределенность в значении координаты, а дельта р – неопределенность в значении импульса. Ну, и так далее, кто знает физику хотя бы в пределах школьного курса, - тем все не надо дадьше рассказывать. Позволю себе лишь наполнить всем - там как? Малая длина волны света, благоприятная для локализации частицы в пространстве координат, означает применение фотонов, несущих большую энергию и способных, ясен пень, сообщить частице большой толчок, и тем самым сильно нарушающих ее локализацию в пространстве импульсов. Применение же фотонов малих энергий означает использование света большой длины волны, что приводит к расширению всех дифракционных полос и к уменьшению точности локализации частицы в обычном (координатном) пространстве.
По моему, Алексей, все в этих двух ребят, Л. Де Бройля и Гейзенберга логично объясняется Волновые свойства в правой стороне, корпускулярные – в левой стороне уравнения. Лямбда умноженная на массу движущейся частицы – эт-т они воспринимали не в соединении каком-то, производящем непостоянного свойства символ М (массу), а в разделении понятий. Потому у них и скорость света С, – константой всегда считалась.
***
Не знаю, прав ли я иль нет в своих выводах, - честно, - Вы немного посеяли во мне какое-то сомнение. Но тут, в принципе, я как и ни при чем, - что я сделал? Просто взял, да и воспроизвел в своей интерпретации рассуждения чужие, воспроизвел так, как это до сих пор понимал.
Читайте также: