Как посчитать момент на колесе
Сразу оговорюсь, что мы строим внедорожный автомобиль. Честный, без понтов.
Для пояснения сути поделюсь таким наблюдением:
Как-то после заезда в дреге я пересел на внедорожник Тойоту и отправился домой. Еду – наслаждаюсь комфортом, после тряски на жёстком корче. И вдруг пришла мысль выяснить цену этого удовольствия… Родился вопрос: А как эта железка проедет 402 метра?
Я остановился, чуть раскрутил двигатель, стартовал, раскрылся, переключился и… расхохотался.
Не проведи я этот эксперимент, и дальше-бы думал, что подо мной находится реально быстрый джип, разгоняющийся так, что «вдавливает в кресло». А по факту он – резкая черепаха.
На самом деле, в нём всё настроено под ощущение динамики. Не под внедорожные качества машины, не под максимальный разгон на асфальте, а под субъективные чувства.
Главная его задача – качать туда-сюда жопу водителя в кресле. Для чего передаточные ряды точно подобраны под… мягкость сидений. Такой «динамикой» хорошо пугать пассажиров, бросая машину вперёд на пару метров, играя газом в проулках города, запруженных другими машинами.
Это природа и беда современного автопрома. Он весь показушный, услужливый, но запредельно лживый.
Нам же нужно, чтобы машина именно ехала. И в грязях, и в князях. Не более того.
Итак, начнём:
Напомню начальные условия движения машины вне дороги, что мы рассматривали ранее. Сила сопротивления качению должна быть меньше тяговой силы на колёсах, а та, в свою очередь, должна быть меньше силы сцепления с дорогой.
Для отдельного колеса полноприводной машины в буковках формул выразим это так:
F сопр.кач. < F кол < F сцепл.
F сопр. кач. = К сопр. кач. (коэффициент сопротивления качению) * G кол. (масса, приходящееся на колесо).
F сцепл. = К сцепл. (коэффициент сцепления)*G кол (масса, приходящаяся на колесо).
Масса, приходящаяся на колесо, G кол – 400 кг.
Посмотрим на цифры коэффициентов сопротивления качению и сцепления для наиболее сложных условий.
Глинистая целина в распутицу:
К сопр. кач. — 0.2-0.3, К сцепл. — 0.15-0.25
Песок сухой:
К сопр. кач. — 0.1-0.3, К сцепл. — 0.2-0.4
Сырой чернозём:
К сопр. кач. — 0.35, К сцепл. — 0.2-0.4
Движение, без привлечения грунтозацепов, здесь условно возможно только в отдельных случаях. Коэффициенты накладываются друг на друга с областью пересечения 0.1-0.4.
То есть, чтобы машина имела возможность двигаться в натяг, F кол должна находиться в диапазоне от 40 (0.1*400) до 160 (0.4*400) кгс.
Момент на колесе будет равным М кол = F кол*R кол, где F-кол тяговая сила на колесе, а R кол – радиус колеса.
Ранее мы выбрали шины с диаметром 31 дюйм, то есть R кол = 393.7 мм, 0.3937 м
М кол минимум = 40*0.3937 = 15.748 кг*м, М кол максимум = 160*0.3937 = 62.992 кг*м
Переведём в ньютоны на метр (*9,80665):
М кол минимум = 15.748 *9,80665 = 154,435 Н*м, М кол максимум = 62.992 *9,80665 = 617,74 Н*м,
Теперь посчитаем нужный крутящий момент на валу двигателя.
По ТЗ коробка у нас АДС, 5 ступеней со следующими передаточными числами:
I передача — 3,83
II передача — 2,16
III передача — 1,29
IV передача — 1,00
V передача — 0,79
R задний ход — 3,52
Далее идёт раздаточная коробка:
прямая передача — 1,00
понижающая передача -1,94
И замыкает ряд мост Тимкен с передаточным числом 4,625 (ранее было 5.125)
На первой пониженной передаче передаточное число равняется:
Кпер.пон = 3.83*1.94*4.625 = 34.365
На первой прямой:
Кпер.пр = 3.83*1*4.625 = 17.714
Рассчитаем момент на валу двигателя, с учётом коэффициента потерь в трансмиссии (примем его за 0.85, что является нормой для нашего класса машин):
M двиг = (М кол*4/ Кпер)/0.85.
Для первой пониженной передачи момент двигателя должен равняться:
М двиг. мин = (154,435*4/34.365)/0.85 = 21.14 Н*м
М двиг. макс = (617,74*4/34.365)/0.85 = 84.59 Н*м
Для первой прямой передачи момент двигателя должен равняться:
М двиг. мин = (154,435*4/17.714)/0.85 = 41.02 Н*м
М двиг. макс = (617,74*4/17.714)/0.85 = 164.1 Н*м
Утомил я вас цифрами и буковками? Предлагаю посмотреть на картинку:
Это кривые момента двигателя и мощности для УМЗ 417.
Как мы видим, с крутящим моментом на валу двигателя мы попадаем тютелька в тютельку, на первой прямой передаче.
Теперь давайте подсчитаем скорость движения автомобиля в диапазоне от 1000 до 5000 оборотов в минуту на валу двигателя (n двиг):
Длина окружности колеса равняется L = 2πR = 2x3,14157*0.3937=2.474м
Обороты колеса равны n кол = n двиг/Кпер
Для первой пониженной передачи, при оборотах 1000, п кол = 1000/34.365 = 29.09 об/мин.
Для первой пониженной передачи, при оборотах 5000, п кол = 5000/34.365 = 145.5 об/мин.
Для первой прямой передачи, при оборотах 1000, п кол = 1000/17.714 = 56.45 об/мин.
Для первой прямой передачи, при оборотах 5000, п кол = 5000/17.714 = 282.26 об/мин.
Скорость, понятно, равняется S = L*n кол.
Для первой пониженной передачи, при оборотах 1000, S = 2.474*29.09 = 71.969 м/мин, т.е. 4.318 км/ч.
Для первой пониженной передачи, при оборотах 5000, S = 2.474*145.5 = 359.967 м/мин, т.е. 21.59 км/ч.
Для первой прямой передачи, при оборотах 1000, S = 2.474*56.45 = 139.657 м/мин, т.е. 8.379 км/ч.
Для первой прямой передачи, при оборотах 5000, S =2.474*282.26 = 698.31 м/мин, т.е. 41.80 км/ч.
Вот тут попадание чуточку хуже.
Суть в том, наилучшая скорость преодоления бездорожья ходом – 30 км/ч (выяснена экспериментальным путём). А комфортная скорость преодоления наиболее опасных участков – 5 км/ч, то есть скорость движения человека. В идеале обе скорости должны достигаться в пределах одной передачи.
На первой прямой передаче 30 км/ч (считаем в обратную сторону, 30 км/ч = 500 м/мин, (500/2.474)*17.714 = 3580 об/мин) практически приходится на пик мощности двигателя – это отлично. Но для движения с наименьшей необходимой скоростью данный двигатель необходимо научить устойчиво работать при 600 об/мин. С достаточно уверенным контролем крутящего момента в диапазоне от 41.02 до 164.1 Н*м. Это прямо противоположное действие от реализации «современных канонов тюнинга двигателей». Т.е. с двигателем надо серьёзно поработать «на низах».
При этом рабочая частота вращения двигателя – 3580 об/мин. На этих оборотах нужно обеспечить максимально комфортный уровень шума. Т.е. звук должен быть именно рабочим, не вызывающим тревоги и напряжения.
Да, забегая вперёд, посчитаем, на какую скорость приходится пик мощности двигателя на пятой повышенной передаче: S = ((4000/0.79)/4.625)*2.474 = 2708.45 м/мин., 162.5 км/ч.
P.S. Юмор этой части истории в том, что заводской размер шин («теза») вновь оказался правильно рассчитанным, шины для варианта «синтез» проходят по самому краю расчётов, а вот «антитеза» – гаражный тюнинг в сторону максимально больших колёс – пролетает мимо кассы.
Нет, конечно, при последующих играх с раздатками и мостами, есть шансы попасть в цель на какой-либо передаче, но лишь одна замена заводских шин на «35 катки и т.д.» это совсем не сулит.
Мы перестали спорить в курилках на технические темы. А жаль. Какой нормальный мужик откажется побазарить о том, как распределяется по колесам крутящий момент мотора? Или хотя бы постоять рядом, храня молчанье в важном споре. Не сериалы же нам обсуждать!
Про мощности и скорости спорить неинтересно, а вот момент — дело другое! Разброд мнений здесь гарантирован. По секрету скажем, что даже «доценты с кандидатами» сгоряча давали противоположные ответы на простые, казалось бы, вопросы. В итоге истину удалось постичь только после длительной дискуссии с представителями заводов ГАЗ и УАЗ и нескольких профильных вузов, а также в результате консультаций с зарубежными коллегами.
Предлагаем всем желающим попытаться найти правильные ответы в предложенных нами ситуациях. А предварительно перечислим условия, которые следует учитывать при выборе правильного варианта.
2-uslovn-Zalacha-diff-CP-222
ВОПРОС № 1
2-1-Zalacha-diff-CP
Автомобиль сел на брюхо и беспомощно крутит ведущими колесами в воздухе. Чему при этом приблизительно равен момент на маховике двигателя?
Б — зависит от оборотов
В — заявленной паспортной величине
Г — зависит от включенной передачи
Правильный ответ: А
Тем, кому непонятен ответ, поясняем: момента без сопротивления не бывает! Представьте себе электрическую розетку, рядом с которой стоит неподключенный утюг. Напряжение в розетке есть, но отдаваемый ток — нулевой. Так и здесь: двигатель не совершает никакой полезной работы, колеса не встречают сопротивления, а потому и момент отсутствует.
* Если это понятно, то даем задание более сложное — уже с участием дифференциала. Тем, кто подзабыл, что это такое, рекомендуем заглянуть в подсказку ниже.
C чем его едят
1-2-Zalacha-diff-CP
Дифференциал (от лат. differentia — разность, различие) — механизм, обеспечивающий вращение ведущих колес с разными скоростями (например, в повороте). Реальные условия движения автомобиля обусловливают разницу в угловых скоростях его колес. Почему? Потому, что они проходят пути разной длины (в повороте или по неровностям) и радиусы качения также различны. Поэтому ведущие колеса работают с участием межколесных и межосевых дифференциалов — чтобы не возникал так называемый паразитный (тормозящий) крутящий момент на одном из колес, как это бывает на поворотной оси телеги с цельной осью. Дифференциал, распределяющий крутящий момент между выходными валами поровну, называют симметричным.
ВОПРОС № 2
Автомобиль ВАЗ‑2107 едет по кругу на четвертой передаче. Как приблизительно распределены моменты на его задних колесах?
2-2-Zalacha-diff-CP
Б — обратно пропорционально частоте вращения каждого из колес
В — в зависимости от силы сцепления с дорогой и от нагрузок
Г — прямо пропорционально частоте вращения каждого из колес
Правильный ответ: А
Моменты распределены поровну: по-другому симметричный дифференциал просто не умеет себя вести. Напоминаем, что трение и прочие потери мы условились не учитывать
*Если и это понятно, то усложняем вопросы.
ВОПРОС № 3
У ВАЗ‑2107 при включенной передаче одно ведущее колесо вывешено в воздухе. Как приблизительно распределены моменты на задних колесах, если принять момент, поступающий от двигателя, за 100%?
2-3-Zalacha-diff-CP
А — 100% на вращающемся колесе и 0% на неподвижном
Б — на обоих колесах момент равен нулю
В — в зависимости от сцепления неподвижного колеса с дорогой
Г — пропорционально оборотам двигателя
Правильный ответ: Б
Почему нулю, если колесо крутится? Дело в том, что полезной работы двигатель не совершает. Висящее колесо не испытывает сопротивления, а потому и момент на нем нулевой. На неподвижном колесе, само собой, момент также равен нулю.
*Теперь переходим к полноприводным автомобилям: здесь к межколесным дифференциалам добавлен межосевой.
ВОПРОС № 4
Chevrolet Niva едет по кругу на четвертой передаче. Включена блокировка межосевого дифференциала. Каково приблизительное соотношение моментов на всех колесах, если принять момент, поступающий от двигателя, за 100%?
2-4-Zalacha-diff-CP
А — по 25% на каждом
Б — по 50% на каждом
В — пропорционально оборотам двигателя
Г — на колесах каждой оси моменты делятся поровну, а распределение по осям — в зависимости от нагрузок и сил сцепления
Правильный ответ: Г
Межколесные дифференциалы на каждой из осей делят моменты поровну, как и в предыдущих примерах. Если бы межосевой дифференциал оставался свободным, каждому колесу досталось бы по 25% крутящего момента. Но водитель его заблокировал, а потому распределение между осями стало зависеть от конкретной дорожной ситуации. В пределе (колеса одной из осей стоят на сухом асфальте, а колеса другой — на гладком льду) практически весь момент реализуется на асфальте.
*А теперь предположим, что мы немножко застряли.
ВОПРОС № 5
У вседорожника Chevrolet Niva при включенной передаче одно ведущее колесо вывешено в воздухе. Водитель заблокировал межосевой дифференциал. Как приблизительно распределены моменты на всех четырех колесах?
2-5-Zalacha-diff-CP
А — на вывешенном колесе 0%, на втором колесе той же оси 0%; на другой оси моменты на каждом из колес равны половине момента, поступающего на ее дифференциал от двигателя
Б — на вывешенном колесе 0%, на остальных — по 33,3% момента, поступающего от двигателя
В — на всех колесах по 25% момента, поступающего от двигателя
Г — в зависимости от нагрузок и сил сцепления
Правильный ответ: А
Висящее в воздухе колесо не работает — следовательно, момент на нем нулевой. То же относится к другому колесу на этой оси: незаблокированный межколесный дифференциал обеспечил равенство. А вот другая ось работает в штатном режиме. И ненулевые моменты на ее колесах при свободном межколесном дифференциале равны между собой.
*Теперь попробуем заблокировать межколесный дифференциал!
ВОПРОС № 6
Полноприводный вседорожник едет по кругу на четвертой передаче. Включена блокировка заднего дифференциала. Межосевой дифференциал не заблокирован. Каково приблизительное соотношение моментов на колесах?
2-6-Zalacha-diff-CP
А — на каждом по 25% момента, поступающего к межосевому дифференциалу от двигателя
Б — на каждом по 50% момента, поступающего от двигателя
В — зависит от оборотов мотора
Г — на передних колесах по 25%. Остальные 50% распределяются между задними колесами пропорционально нагрузке на них и силам сцепления.
Правильный ответ: Г
Благодаря работающему межосевому дифференциалу задний мост получает столько же ньютон-метров, сколько и передний. Но реальное соотношение моментов на его колесах уже зависит от конкретной дорожной ситуации, поскольку блокированный межколесный дифференциал ничего не выравнивает. Если одно из колес зависнет в воздухе, то всё достанется второму колесу, а если сцепление одинаковое, то и дележ будет равным. Поэтому соотношение моментов определяется нагрузками и силами сцепления. ;
*Попытаемся застрять еще раз.
ВОПРОС № 7
У полноприводного вседорожника при включенной передаче одно заднее колесо вывешено в воздухе. Включена блокировка заднего дифференциала. Межосевой дифференциал не заблокирован. Каково примерное соотношение моментов на колесах, если условно принять момент, поступающий от двигателя, за 100%?
2-7-Zalacha-diff-CP
А — 100% на колесе, касающемся земли, 0% на вывешенном и по 25% на передних колесах
Г — 50% на колесе, касающемся земли, 0% на вывешенном и по 25% на передних колесах
Правильный ответ: Г
Межосевой дифференциал поделил моменты между осями поровну. Висящее колесо не испытывает сопротивления, а потому его момент равен нулю. За него отдувается другое колесо на этой оси, толкающее машину, — и весь передающийся назад крутящий момент (50% общего) достается именно второму колесу.
*Напоследок напомним основные принципы, которые помогут разобраться в моментах, осях и дифференциалах.
- Там, где нет сопротивления, момент всегда равен нулю.
- Заблокированный межколесный дифференциал фактически превращает ось автомобиля в аналог колесной пары железнодорожного вагона. Но даже при этом момент на вывешенном колесе равен нулю.
- На вывешенном колесе момент равен нулю независимо от того, блокирован дифференциал или нет.
- Симметричный дифференциал всегда выравнивает моменты: межосевой — на осях, межколесный — на колесах.
Всем удачи на дорогах — без зависших колес и нулевых моментов!
Как работает дифференциал
Дифференциал состоит из корпуса (1), шестерен-сателлитов (2) и полуосевых шестерен (3). Корпус обычно совмещен с ведомой шестерней главной передачи (4). Шестерни-сателлиты играют роль планетарного механизма и соединяют полуосевые шестерни с корпусом дифференциала. Полуосевые (солнечные) шестерни соединены с ведущими колесами через полуоси.
Ведомая шестерня главной передачи вращает корпус с сателлитами, который в свою очередь вращает шестерни полуосей. Когда автомобиль движется идеально прямо, сателлиты неподвижны относительно своих осей. Но как только движение становится неравномерным (например, при повороте), сателлиты начинают собственные фуэте, ускоряя одну полуось и замедляя другую.
Если сцепление колес с покрытием разное, то крутящий момент, реализуемый на скользком покрытии, ограничен коэффициентом сцепления шины с дорогой. Чем меньше сопротивление, тем ниже момент на этом колесе. Но таким же становится момент и на другом колесе той же оси. А вот если заблокировать дифференциал, то дележка моментов между колесами происходит в соответствии с силами их сопротивлений (или сцеплений) с дорогой.
В так называемых дифференциалах повышенного трения сателлиты изначально лишены возможности вращаться свободно. Это сделано как раз для того, чтобы при вывешивании или проскальзывании одного колеса машина беспомощно не застревала. Если с обычным дифференциалом в таких случаях моменты на колесах падают до нуля, то его «коллега» с повышенным трением оставляет им запас, равный заложенному в него моменту трения! Получается эдакий облегченный вариант полной блокировки, помогающий выбраться из неприятных ситуаций, если это позволяет сила трения на колесе с лучшим сцеплением.
Область классической механики включает изучение тел в движении, особенно физические законы, касающиеся тел, находящихся под воздействием сил. Большинство механических аспектов проектирования роботов тесно связано с концепциями из этой области. В данном блоке описываются несколько ключевых применяемых концепций классической механики.
СКОРОСТЬ - это мера того, насколько быстро перемещается объект. Обозначает изменение положения во времени (проще говоря, какое расстояние способен преодолеть объект за заданный период времени). Данная мера представлена в единицах расстояния, взятых в единицу времени, например, в количестве миль в час или футов в секунду.
ЧАСТОТА ВРАЩЕНИЯ – Скорость может также выражаться во вращении, то есть насколько быстро объект движется по кругу. Измеряется в единицах углового перемещения во времени (то есть в градусах в секунду), или в циклах вращения в единицу времени (например, в оборотах в минуту). Когда измерения представлены в оборотах в минуту (RPM), речь идет о частоте вращения. Есть речь идет об об/мин автомобильного двигателя, это означает, что измеряется скорость вращения двигателя.
УСКОРЕНИЕ – Изменение скорости во времени представляет собой ускорение. Чем больше ускорение, тем быстрее изменяется скорость. Если автомобиль развивает скорость от 0 до 60 миль в час за две секунды, в этом случае ускорение больше, чем когда он развивает скорость от 0 до 40 миль в час за тот же период времени. Ускорение - это мера изменения скорости. Отсутствие изменения означает отсутствие ускорения. Если объект движется с постоянной скоростью - ускорение отсутствует.
СИЛА - Ускорение является следствием воздействия сил, которые провоцируют изменение в движении, направлении или форме. Если вы нажимаете на объект, это означает, что вы прикладываете к нему силу. Робот ускоряется под воздействием силы, которую его колеса прикладывают к полу. Сила измеряется в фунтах или ньютонах.
Например, масса объекта воздействует на объект как сила вследствие гравитации (ускорение объекта в направлении центра Земли).
КРУТЯЩИЙ МОМЕНТ – Сила, направленная по кругу (вращение объекта), называется крутящим моментом. Крутящий момент - это вращающая сила. Если к объекту приложен крутящий момент, на границе первого возникает линейная сила. В примере с колесом, катящемся по земле, крутящий момент, приложенный к оси колеса, создает линейную силу на границе покрышки в точке ее контакта с поверхностью земли. Так и определяется крутящий момент - как линейная сила на границе круга. Крутящий момент определяется величиной силы, умноженной на расстояние от центра вращения (Сила х Расстояние = Крутящий момент). Крутящий момент измеряется в единицах силы, умноженной на расстояние, например, фунто-дюймах или ньютон-метрах.

В примере с колесом, катящемся по земле, если известен крутящий момент, приложенный к оси с закрепленным на ней колесом, мы можем рассчитать количество силы, прикладываемой колесом к поверхности. В этом случае, радиус колеса является расстоянием силы от центра вращения.
Сила = Крутящий момент/Радиус колеса

В примере с рукой робота, удерживающей объект, мы можем рассчитать крутящий момент, требуемый для поднятия объекта. Если объект обладает массой, равной 1 ньютону, а рука имеет длину 0,25 метра (объект располагается на расстоянии 0,25 метра от центра вращения), тогда
Крутящий момент = Сила х Расстояние = 1 ньютон х 0,25 метра = 0,25 ньютон-метров.
Это означает, что для удержания объекта в неподвижном положении, необходимо применить крутящий момент, равный 0,25 ньютон-метров. Чтобы переместить объект вверх, роботу необходимо приложить к нему крутящий момент, значение которого будет превышать 0,25 ньютон-метров, так как необходимо преодолеть силу гравитации. Чем больше крутящий момент робота, тем больше силы он прикладывает к объекту, тем больше ускорение объекта, и тем быстрее рука поднимет объект.


Для данных примеров, мы можем рассчитать крутящий момент, необходимый для подъем этих объектов.
Пример 7.2 - Крутящий момент = Сила х Расстояние = 1 ньютон х 0,125 метра = 0,125 ньютон-метров.
Для данного примера, длина рука равна половине длины руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза меньше. Значение длины руки пропорционально значению требуемого крутящего момента. При равных исходных характеристиках объекта, чем короче рука, тем меньший крутящий момент необходим для подъема.
Пример 7.3 - Крутящий момент = Сила * Расстояние = 1 ньютон х 0,5 метра = 0,5 ньютон-метров.
Для данного примера, длина рука равна удвоенной длине руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза больше.
Еще одна точка зрения относительно ограниченного крутящего момента в соединении руки робота заключается в следующем: более короткая рука сможет поднять объект большей массы, чем более длинная рука; однако, для первой доступная высота подъема объекта будет меньше, чем для второй.


Эти примеры иллюстрируют руку робота, поднимающую объекты разной массы. Какова взаимосвязь с требуемым количеством крутящего момента?
Пример 4 - Крутящий момент = Сила х Расстояние = ½ ньютона х 0,25 метра = 0,125 ньютон-метров.
Пример 5 - Крутящий момент = Сила х Расстояние = 2 ньютона х 0,25 метра = 0,5 ньютон-метров.
Эти примеры иллюстрируют уменьшение значения требуемого крутящего момента по мере снижения массы объекта. Масса пропорциональна крутящему моменту, необходимому для ее подъема. Чем тяжелее объект, тем больше крутящий момент, требуемый для его подъема.
Проектировщики роботов должны обратить внимание на ключевые взаимосвязи между значениями крутящего момента, длины руки и массы объекта.
РАБОТА – Мера силы, приложенной на расстоянии, называется работой. Например, для удерживания объекта необходимо 10 фунтов силы. Далее, чтобы поднять этот объект на высоту 10 дюймов, требуется определенное количество работы. Количество работы, требуемое для подъема объекта на высоту 20 дюймов, удваивается. Работа также понимается как изменение энергии.
МОЩНОСТЬ - Большинство людей полагает, что мощность является термином из области электрики, но мощность также относится и к механике.
Мощность - это количество работы в единицу времени. Насколько быстро кто-то может выполнить работу?
В робототехнике принято понимать мощность как ограничение, так как соревновательные робототехнические системы имеют ограничения в части выходной мощности. Если роботу требуется поднять массу в 2 ньютона (прилагая 2 ньютона силы), скорость подъема будет ограничиваться количеством выходной мощности робота. Если робот способен произвести достаточное количество мощности, он сможет быстро поднять объект. Если он способен произвести лишь малое количество энергии, подъем объекта будет производиться медленно (либо не будет производиться вообще!).

Мощность определяется как Сила, умноженная на Скорость (насколько быстро выполняется толчок при постоянной скорости), и обычно выражается в Ваттах.
Мощность [Ватты] = Сила [Ньютоны] х Скорость [Метры в секунду]
1 Ватт = 1 (Ньютон х Метр) / Секунда
Как это применяется в соревновательной робототехнике? К проектам роботов применяются определенные ограничения. Проектировщики соревновательных роботов, использующие систему проектирования VEX Robotics Design, также должны учитывать физические ограничения, связанные с применением электромоторов. Электромотор обладает ограниченной мощностью, поэтому он может производить только определенное количество работы с заданной скоростью.
Примечание: все перспективные концепции имеют базовое описание. Более глубоко обсуждать эти физические свойства учащиеся будут в процессе обучения в ВУЗах, если выберут область STEM в качестве направления обучения.
Пользуясь случаем хотелось бы пролить свет на вечные споры о мощности и крутящем моменте двигателей внутреннего сгорания. Одни считают главным показателем максимальную мощность мотора, другие ставят во главу угла крутящий момент. Встречаются люди, которые считают, что 100 «дизельных» л.с. соответствуют примерно 140 «бензиновым» л.с. Также бытует мнение, что VW Golf TDI c 330 Нм крутящего момента будет ускоряться лучше, чем Porsche 911 с 320 Нм.
Пользуясь случаем хотелось бы пролить свет на вечные споры о мощности и крутящем моменте двигателей внутреннего сгорания. Одни считают главным показателем максимальную мощность мотора, другие ставят во главу угла крутящий момент. Встречаются люди, которые считают, что 100 «дизельных» л.с. соответствуют примерно 140 «бензиновым» л.с. Также бытует мнение, что VW Golf TDI c 330 Нм крутящего момента будет ускоряться лучше, чем Porsche 911 с 320 Нм.
Очевидно, что эти утверждения не соответствуют действительности.
Определения и разъяснения:
Крутящий момент:
Крутящий момент двигателя прилагается к коленчатому валу двигателя или к первичному валу коробки передач. Крутящий момент изменяется в зависимости от частоты вращения двигателя. Крутящий момент на колесах зависит от передаточного отношения трансмиссии.
Крутящий момент на колесах:
Это преобразованный трансмиссией крутящий момент двигателя.
Мощность двигателя непосредственно взаимосвязана с крутящим моментом двигателя, а именно, через соотношение P=M*n/9550, где М- крутящий момент двигателя. Единица измерения 1 Н*м, n – частота вращения двигателя в об/мин.
Диаграммы крутящего момента достаточно, чтобы просчитать кривую мощности (и наоборот).

Возьмем два двигателя. У обоих максимальный крутящий момент 200 Нм при 4000 об/мин и мощность 147 л.с. при 6000 об/мин. Несмотря на то, что основные данные этих двух моторов одинаковы, они все же отличаются по динамическим характеристикам. Диапазон крутящего момента и мощности первого двигателя лучше чем у второго. Предположим, что переключение передач происходит при 6500 об/мин и обороты двигателя на следующей, более высокой передаче опускаются до 4300 об/мин. Первый двигатель имеет до точки при 6000 об/мин непрерывно больший крутящий момент и мощность. Таким образом, первый автомобиль будет ускоряться лучше. Это показывает, что основные данные двигателя дают только частичную информацию.
Так что мы теперь знаем о «крутящем моменте» и «мощности двигателя»? На самом деле сравнительно мало. Поскольку трансмиссия и ее передаточное отношение играю существенную роль в движении автомобиля. Старые американские автомобили были оборудованы 2-3 ступенчатыми коробками передач, и несмотря на значительные мощности двигателей, разгонялись они достаточно скромно, т.к. падение оборотов при переключении передач было слишком большим. Как грубое сравнение можно привести Mercedes S-Klasse. Он оборудован 7-ступенчатым автоматом, который позволяет полностью использовать имеющуюся в распоряжении мощность двигателя.
Почему это так?
Все мы знаем, что ускоряется автомобиль лучше в определенной области оборотов двигателя. Оптимально, когда обороты двигателя постоянно находятся в этом диапазоне. Но это возможно лишь на немногих автомобилях оборудованных CVT (безступенчатыми трансмиссиями).
Чем больше передач имеется в распоряжении, тем меньше становится скачок оборотов и тем ближе мы становимся к оптимальному числу оборотов двигателя между переключениями. Усилие на ведущих колесах, это то, что приводит автомобиль в движение. Это сила, приложенная по касательной к окружности колеса. Она несет в себе всю информацию (Крутящий момент, передаточное отношение трансмиссии, размер колес) и направлена противоположно силе сопротивления движению и силе инерции.
Когда нужно переключаться?
Оптимальная точка переключения достигается тогда, когда на следующей высшей передаче имеется большее усилие на ведущих колесах чем на актуальной передаче. Чтобы найти оптимальную точку переключения, необходимо воспользоваться кривой крутящего момента. Диаграмма тягового усилия на ведущих колесах зависит от передаточного отношения трансмиссии и размера установленных шин. Как только пересекутся кривые отдельных передач, нужно переключиться на следующую передачу, чтобы достичь лучшего ускорения. Если же кривые не пересекаются, тогда следует выкручивать двигатель до ограничителя. Далее отображены диаграммы тягового усилия на ведущих колесах, чтобы можно было прочувствовать теорию в деле.
Влияние передаточного отношения
Турбодизель достигает очень высоких значений крутящего момента при низких оборотах двигателя.
Но это только цифры, по которым можно судить о том, как автомобиль будет ускоряться и по ним нельзя делать окончательные выводы. Почему? Потому что дизелю нужно значительно дольше переключаться, чтобы достичь одинаковую с бензином скорость(т.к. число оборотов дизеля существенно ниже чем у бензинового двигателя). Это приводит к тому, что бензиновый двигатель свой низкий крутящий момент преобразует значительно лучше за счет коротких передач, чем дизель с длинными передачами.
Турбодизель против высокооборотистого атмосферного двигателя.
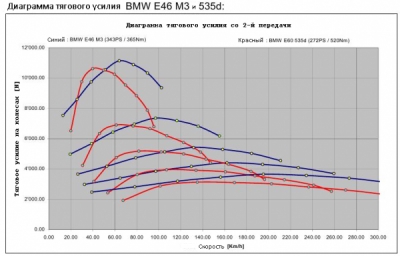
Несмотря на длинные передаточные отношения дизель как правило имеет лучшую тяговитость при низких оборотах. Наглядно это отображено на диаграмме сравнения BMW М3 3.2 л двигателя и BMW 535d. Несмотря на гигантский крутящий момент дизеля (520Нм), бензиновый двигатель (365Нм) в очень широком диапазоне оборотов двигателя имеет значительно большее тяговое усилие на ведущих колесах. Так что этот бензиновый двигатель (вопреки многим мнениям) может ездить с редкими переключениями, иногда даже ленивее чем 535d (на шестой передаче тяговое усилие на колесах стабильно выше чем у 535d, независимо при каких оборотах и какой скорости). Но можно говорить о том, что большая часть турбированных двигателей имеет лучшую приемистость (на низких оборотах) чем атмосферные двигатели. Так что предпочитаете ли вы двигатели имеющие «подрыв» на низких скоростях, или те, которые выдают тягу плавно, это остается делом вкуса.

Турбодизель против турбобензина
Сравним BMW E90 335i с 306 л.с. и 400 Нм и BMW E90 335d с 286 л.с. и 560 Нм. На низших передачах в среднем диапазоне оборотов тяга на колесах дизеля существенно выше, чем у бензинового двигателя. При высоких оборотах бензин свою мощность отыгрывает. На 6-й передаче бензин имеет стабильно большее усилие на колесах чем дизель.
Диаграмма тягового усилия BMW E90 335i и E90 335d

Дизель или бензин как тягач
Широко распространено мнение, что дизельный двигатель из-за его высокого крутящего момента лучше подходит для буксировки. Тем не менее из-за огромного скачка в развитии бензиновых двигателей это не совсем верно. Современные бензиновые двигатели все чаще оснащаются турбонагнетателями, которые могут создавать достаточное давление наддува при низких оборотах, и следовательно достигать высокого крутящего момента. Сравним двигатели 1.4 TSI (170 л.с., 240 Нм) и 2.0TDI (170 л.с., 350 Нм) в VW Golf5.
За основу взят 5% уклон, коэффициент лобового сопротивления 0.7, площадь лобового сопротивления 5.87 м2 и общая масса 3250 кг. 1-я передача для лучшего рассмотрения исключена.
Все режимы выше голубой линии возможны с вышеназванными условиями. Все режимы ниже голубой линии ведут к снижению скорости и в конечном счете к переходу на низшую передачу. Можно увидеть, что дизель может использовать первые четыре передачи, TSI – первые пять. Максимально допустимые скорости следующие:
TDI:
68 км/ч на второй передаче (в ограничителе оборотов)
104 км/ч на третьей передаче (вблизи ограничителя оборотов около 4400 об/мин)
TSI:
99 км/ч на второй передаче (вблизи ограничителя оборотов около 7000 об/мин)
106 км/ч на третьей передаче (при около 5500 об/мин)
90 км/ч на четвертой передаче (при около 3500 об/мин)
65 км/ч на пятой передаче (при около 2300 об/мин)
В целом TSI гораздо лучше подходит для движения с прицепом. Единственным недостатком может быть значительный рост расхода топлива у бензина.


Как выглядит диаграмма тягового усилия авто со ступенчатыми коробками передач мы уже знаем.
Для полноты картины следует отметить бесступенчатую трансмиссию Audi «Multitronic».

Рассмотрим кратко, так как эта трансмиссия имеет призрачные шансы на существование. Это безступенчатая трансмиссия с различными профилями вождения. Спортивно настроенный водитель использует голубую линию для максимального ускорения, с высокими оборотами и большим расходом. Средний водитель будет использовать более низкие обороты. А значит тяга на колесах будет не так высока как в спорт режиме. Соответственно автомобиль ускоряется медленнее. CVT, как уже говорилось ранее, превосходное решение. Теоретически она позволяет получить максимальную производительность. На практике все выглядит по другому. Авто с Мультитроником ускоряются хуже, чем авто с МКПП. Потери в трансмиссии слишком велики и перекрывают все преимущества.
А что же насчет двигателей грузовиков и коммерческих автомобилей?
Глядя на кривые мощности и крутящего момента грузовиков можно быстро обнаружить существенные отличия от легковых автомобилей. В то время как на двигателях легковых авто целью является как можно более равномерное и высокое значение крутящего момента, двигателям грузовиков необходим пик крутящего момента. Покажем качественные отличия грузовых и легковых турбодизелей:

Почему так?
Области применения полностью различны. Легковому автомобилю необходимо достичь максимального ускорения и как можно более высокой максимальной скорости. В тоже время необходимо принять во внимание тот факт, что эти двигатели практически постоянно используются в режимах частичной нагрузки. Грузовые же двигатели (в качестве простого примера возьмем двигатели бульдозера или трактора) обычно используются на максимальной нагрузке. Максимальные крутящие момент и мощность ему необходимы при низких оборотах, а также как можно большее нарастание крутящего момента. Почему не падение а именно нарастание крутящего момента станет ясно в следующем абзаце.
Цель этого нарастания величины крутящего момента может быть хорошо объяснена на примере бульдозера. Насыпь земли перед ковшом бульдозера всегда большая, поэтому возникает необходимость увеличить мощность, чтобы продвинуть насыпь дальше. При этой нагрузке частота вращения двигателя падает и вместе с тем падает скорость сдвига. Снижение числа оборотов двигателя благодаря типичной для грузовых транспортных средств кривой крутящего момента ведет к росту крутящего момента и мощности двигателя (смотри график). Таким образом в некоторой степени предотвращается дальнейшее падение оборотов и скорости сдвига – чем сильнее падение числа оборотов, тем больше мощности отдает двигатель. В переносном смысле можно сказать: кривая крутящего момента таких двигателей позволяет независимо от нагрузки относительно сохранять необходимую скорость. Такие моторы имеют «иммунитет» против увеличения нагрузки и становятся ненамного медленнее при ее увеличении. Но все же почему «нарастание крутящего момента» а не «падение»? Теперь нужно смотреть на график в направлении рабочих оборотов. При нагрузке число оборотов падает и происходит РОСТ крутящего момента.

В первой части мы рассмотрели понятия мощности и момента двигателя. Теперь же посмотрим что происходит на колесах. Как зависит момент на колесах от текущей передачи. На каких оборотах двигателя лучше переключаться для наибольшей топливной экономичности и для интенсивного разгона. Посмотрим видео разгона VW Polo GTI с коробкой DSG7 до максимальной скорости.
Возьмем автомобиль VW Polo GTI с рядной четверкой объемом 1,4 л с непосредственным впрыском и наддувом от нагнетателя и турбокомпрессора. Двигатель развивает 180 л.с. (на 6200 об/мин) и за счет «двойного» наддува имеет полку момента в 250 Н·м в диапазоне с 2000 до 4500 об/мин.

VW Polo GTI с коробкой DSG7. Максимальная скорость 229 км/ч
Момент и мощность на колесах
Мощность на оси колес примерно равна мощности выдаваемой двигателем за вычетом КПД трансмиссии и всех вращающихся компонентов между колесами и двигателем. Момент же может сильно отличаться в зависимости от выбранной передачи. Момент на оси колес равен моменту на двигателе, умноженному на произведение передаточного числа передачи в коробке и главной пары в дифференциале. Каждая передача характеризуется своим передаточным числом, равным отношению количества зубцов на шестернях. Высшие передачи могут иметь передаточное число меньше единицы, но из-за понижающей пары в дифференциале на колеса все равно передается больший момент. Скорость же вращения колес падает прямо пропорционально росту момента. Также нужно принимать во влияние радиус колес. Чем он больше, тем меньше крутящего момента с двигателя будет прикладываться для движения автомобиля, но тем быстрее он будет ехать.
Рассмотрим момент, передаваемый на колеса, в зависимости от передачи.

Зависимость момента на колесах от их угловой скорости на разных передачах. Для сравнения приведен момент на коленвале двигателя в зависимости от его угловой скорости
Коробка передач имеет передаточное число для первой передачи равное 15,53. Это означает что момент на оси колеса будет умножен почти в 15 раз. Для момента на двигателе в 250 Н·м момент на колесах будет равен 3880 Н·м. Но при этом максимальная угловая скорость колеса будет составлять 419 об/мин при оборотах двигателя 6500 и этим будет обусловлена максимальная скорость на первой передачи.
Рассмотрим зависимость момента от скорости. Для диска с параметрами 7Jx17 и покрышек с профилем 215/40 радиус колеса составляет 0,3 м. Зная угловую скорость колеса легко вычислить скорость автомобиля.

Зависимость момента на колесах от скорости автомобиля
Обратим внимание на то, что на первой передаче момент на колесах при оборотах двигателя в 6500 об/мин больше, чем для всего диапазона второй передачи. Хотя момент на двигателе меньше, чем если бы мы переключились на вторую передачу. Это означает что для сохранения максимального момента на колесах переключаться с первой на вторую стоит лишь тогда, когда двигатель упрется в ограничитель оборотов, несмотря на то, что мы прошли уже и максимум момента и максимум мощности на двигателе.
Тоже самое справедливо и для второй передачи, а начиная с третьей, передаточные отношения передач подобраны так, что момент для переключения передач (для сохранения максимального момента на колесах) смещается на более ранние обороты и проходит где-то в районе максимума мощности.
Режим экономии топлива
Режим максимальной экономии топлива характеризуется движением на малых оборотах. Ведь для поднятия оборотов нужно больше открыть дроссельную заслонку, впуская больше воздуха в двигатель. А пропорционально росту воздуха будет расти и потребление топлива. При этом, чтобы езда была уверенной необходимо ехать на максимальном моменте. (Кроме того двигатель развивая максимальный момент будет работать экономичнее чем даже на меньших оборотах, но идя «внатяг»). Для этого нужно переключать передачи так, чтобы обороты двигателя на следующей передачи попадали в зону (начала полки) максимального момента.
Рассмотрим зависимость скорости автомобиля в зависимости от оборотов двигателя на разных передачах в режиме экономии топлива.

Красной стрелкой отмечена скорость на разных передачах
Очень кстати приходится наличие «двойного» наддува, позволяющего получить максимум момента начиная с 2000 об/мин. А наличие семиступенчатой коробки DSG позволяет в полной мере реализовать тяговитость низов. Автоматы с двойным сцеплением имеют очень быстрое время переключения передач, а благодаря плавной передачи момента с одной передачи на другую, делают переключение очень плавным (без рывков). Все это позволяет двигаться на скорости 90 км/ч при 2000 об/мин (максимальные обороты при разгоне при этом не превышают 3000 об/мин). Этим достигается крайне эффективный с точки зрения топливной экономичности режим передвижения. Большое количество ступеней нужно для экономичного передвижения на невысоких оборотах. Заявленный расход в смешанном цикле составляет 6л/100км.
Режим интенсивного разгона
Интенсивный разгон характеризуется переключением передач таким образом, чтобы на колесах был наибольший момент. Причем, как мы уже выяснили, в зависимости от передаточных чисел передач может быть так, что момент на колесах на текущей передаче больше чем на следующей, хотя момент на двигателе наоборот меньше.

Зависимость скорости от оборотов двигателя на разных передачах в режиме интенсивного разгона. Пунктиром приведены характеристики двигателя — момент и мощность
В заключении посмотрим видео с разгоном автомобиля до максимальной скорости. DSG7 в режиме Sport не включает седьмую передачу.
Читайте также:

