Максимальное давление колеса на рельс
3.7 Определить среднюю величину, среднее квадратическое отклонение и максимально вероятную величину расчетной нагрузки от колеса на рельс, если статическая нагрузка от веса экипажа на колесо Pст = 100000 Н, а среднее значение силы инерции от колебания кузова на рессорах = 16800 Н, среднее квадратическое отклонение нагрузки от колебания надрессорного строения Sр = 1800 Н, от сил инерции необрессоренных масс, вызванных: неровностью на пути Sнп = 9200 Н, изолированной неровностью на колесе Sинк = 15000 Н, непрерывной неровностью на колесе Sннк = 2000 Н.
3.7Определить среднюю величину, среднее квадратическое отклонение и максимально вероятную величину расчетной нагрузки от колеса на рельс, если статическая нагрузка от веса экипажа на колесо Pст = 143139 Н, а среднее значение силы инерции от колебания кузова на рессорах = 15592 Н, среднее квадратическое отклонение нагрузки от колебания надрессорного строения Sр = 3598 Н, от сил инерции необрессоренных масс, вызванных: неровностью на пути Sнп = 8209 Н, изолированной неровностью на колесе Sинк = 15363 Н, непрерывной неровностью на колесе Sннк = 1330 Н.
Решение задачи
Среднее значение расчетной нагрузки от колеса на рельс определяется по формуле
Здесь Pст – статическая нагрузка колеса на рельс;
– среднее значение динамической добавки от колебания кузова на рессорах.
Расчетная нагрузка определяется по формуле
Численные значения Pрасч и Sрасч составят
3.8 Определить эквивалентную нагрузку от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения изгибающего момента при средней величине расчетной нагрузки = 122000 Н, величине среднего квадратического отклонение расчетной нагрузки = 14500 Н и коэффициента относительной жесткости подрельсового основания и рельса k = 1,421 м -1 .
Определить эквивалентную нагрузку от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения изгибающего момента при средней величине расчетной нагрузки = 158731 Н, величине среднего квадратического отклонение расчетной нагрузки = 9687 Н и коэффициента относительной жесткости подрельсового основания и рельса k = 1,421 м -1 .
Решение задачи
Определим вначале Pрасч по формуле
Максимальная эквивалентная нагрузка для расчета изгибных напряжений в рельсах определяется по формуле
где – ординаты линии влияния изгибающих моментов рельса в сечениях пути xi, расположенных под колесными нагрузками тележки на расстоянии xi от, смежных с расчетной осью
Расчет ведется для системы, состоящей из трех колесных нагрузок.
Для этого случая координаты средних нагрузок равны x1 = l1, x2 = l1 + l2. Причем для двухосной тележки l2 –– это расстояние между крайней осью первой тележки и первой осью следующей по ходу поезда тележки.
Значения расстояний l1 и l2 для четырехосного грузового вагона
x1 = l1 = 1,85 м; x2 = l1 + l2 = 1,85 + 6,75 = 8,6 м.
Ординаты линии влияния изгибающих моментов рельса
Максимальная эквивалентная нагрузка для расчетов напряжений в рельсах от изгиба определяется по формуле
3.9 Определить эквивалентную нагрузку от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения прогиба рельса и нагрузки рельса на шпалу при средней величине расчетной нагрузки = 121900 Н, величине среднего квадратического отклонение расчетной нагрузки = 14600 Н и коэффициента относительной жесткости подрельсового основания и рельса k = 1,421 м -1 .
Определить эквивалентную нагрузку от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения прогиба рельса и нагрузки рельса на шпалу при средней величине расчетной нагрузки = 158731 Н, величине среднего квадратического отклонение расчетной нагрузки = 9687 Н и коэффициента относительной жесткости подрельсового основания и рельса k = 1,421 м -1 .
Решение задачи
Максимальная величина эквивалентной нагрузки определяется по формуле
где – ординаты линии влияния давлений рельса на шпалы в сечениях пути xi, расположенных под колесными нагрузками на расстоянии xi от осей тележки, смежных с расчетной осью
В этом случае при расчете координаты средних нагрузок равны x1 = l1, x2 = l2.
Определим вначале Pрасч по формуле
Ординаты линии влияния давления рельса на шпалу определяются следующим образом
Максимальная величина эквивалентной нагрузки для определения давления рельса на шпалу:
3.10 Определить напряжения изгиба в подошве рельса: осевые σпо и кромочные σпк при воздействии эквивалентной нагрузки = 141800 Н, коэффициенте относитлеьной жесткости подрельсового основания и рельса k = 1,421 м -1 , моменте сопротивления поперечного сечения рельса относительно подошвы Wп = 417·10 -6 м3 , коэффициенте учета внецентренного приложения вертикальных и горизонтальных поперечных сил f = 1,4.
Определить напряжения изгиба в подошве рельса: осевые σпо и кромочные σпк при воздействии эквивалентной нагрузки = 167356 Н, коэффициенте относитлеьной жесткости подрельсового основания и рельса k = 1,4214 м -1 , моменте сопротивления поперечного сечения рельса относительно подошвы Wп = 417·10 -6 м3 , коэффициенте учета внецентренного приложения вертикальных и горизонтальных поперечных сил f = 1,33.
Решение задачи
Нормальные изгибные напряжения в подошве рельса находятся по общеизвестной формуле
где М – изгибающий момент;
Wп – момент сопротивления относительно наиболее удаленного волокна.
Напряжения в кромке подошвы рельса определяется по формуле
f – коэффициент, переводящий осевые напряжения в подошве в кромочные напряжения; он учитывает влияние горизонтальных поперечных сил Н и внецентренное приложение вертикальных сил Р.
Изгибающий момент в рельсе от воздействия эквивалентной нагрузки
Осевые изгибные напряжения в подошве рельса
Изгибные напряжения в кромке подошвы рельса
3.11 Определить напряжения изгиба в подошве рельса: осевые σпо и кромочные σпк от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если величина расчетной нагрузки Pрасч = 158000 Н, средняя величина расчетной нагрузки = 132000 Н, коэффициенте относительной жесткости подрельсового основания и рельса k = 1,421 м -1 , момент сопротивления поперечного сечения рельса относительно подошвы Wп = 417·10 -6 м3 , коэффициент учета внецентренного приложения вертикальных и горизонтальных поперечных сил f = 1,37.
Определить напряжения изгиба в подошве рельса: осевые σпо и кромочные σпк от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если величина расчетной нагрузки Pрасч = 182946 Н, средняя величина расчетной нагрузки = 158731 Н, коэффициенте относительной жесткости подрельсового основания и рельса k = 1,4214 м -1 , момент сопротивления поперечного сечения рельса относительно подошвы Wп = 417·10 -6 м3 , коэффициент учета внецентренного приложения вертикальных и горизонтальных поперечных сил f = 1,33.
Решение задачи
Нормальные изгибные напряжения в подошве рельса находятся по общеизвестной формуле
где М – изгибающий момент;
Wп – момент сопротивления относительно наиболее удаленного волокна.
Напряжения в кромке подошвы рельса определяется по формуле
f – коэффициент, переводящий осевые напряжения в подошве в кромочные напряжения; он учитывает влияние горизонтальных поперечных сил Н и внецентренное приложение вертикальных сил Р.
Изгибающий момент в рельсе от воздействия эквивалентной нагрузки определяется по формуле
Максимальная эквивалентная нагрузка для расчета изгибных напряжений в рельсах определяется по формуле
где – ординаты линии влияния изгибающих моментов рельса в сечениях пути xi, расположенных под колесными нагрузками тележки на расстоянии xi от, смежных с расчетной осью
Для заданных условий координаты средних нагрузок равны x1 = l1, x2 = l1 + l2. Причем для двухосной тележки l2 – это расстояние между крайней осью первой тележки и первой осью следующей по ходу поезда тележки.
Значения расстояний l1 и l2 для четырехосного грузового вагона
x1 = l1 = 1,85 м; x2 = l1 + l2 = 1,85 + 6,75 = 8,6 м.
Ординаты линии влияния изгибающих моментов рельса
Максимальная эквивалентная нагрузка для расчетов напряжений в рельсах от изгиба определяется
Изгибающий момент в рельсе от воздействия эквивалентной нагрузки
Осевые изгибные напряжения в подошве рельса
Изгибные напряжения в кромке подошвы рельса
3.12 Определить напряжения сжатия в резиновых прокладках на шпалах σш и в балластном слое под шпалой σб от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если средняя величина расчетной нагрузки = 131500 Н, среднее квадратическое отклонение расчетной нагрузки Sрасч = 63000 Н, расстояние между осями шпал lш = 0,5 м, коэффициент относительной жесткости подрельсового основания и рельса k = 1,43 м -1 , площадь прокладки ω = 518·10 -4 м2 и опорная площадь полушпалы Ωα = 2975·10 -4 м2 .
Определить напряжения сжатия в резиновых прокладках на шпалах σш и в балластном слое под шпалой σб от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если средняя величина расчетной нагрузки = 158731 Н, среднее квадратическое отклонение расчетной нагрузки Sрасч = 9687 Н, расстояние между осями шпал lш = 0,5 м, коэффициент относительной жесткости подрельсового основания и рельса k = 1,4214 м -1 , площадь прокладки ω = 210·10 -4 м2 и опорная площадь полушпалы Ωα = 2975·10 -4 м2 .
Решение задачи
В начале определим расчетную нагрузку от колеса на рельс
Для заданных условий
Напряжения смятия в деревянных шпалах под подкладками и в прокладках при железобетонных шпалах определяются по формуле
где Q – давление колеса на рельс;
w – площадь передачи давления на шпалу через подкладку или прокладку (при бесподкладочном скреплении типа ЖБР).
Напряжения в балластном слое под шпалой в подрельсовом сечении определяется по формуле
где 0,5аb – площадь полушпалы (а и b – длина и ширина шпалы);
α – коэффициент изгиба шпалы;
Ωα – эффективная площадь полушпалы с учетом изгиба.
Давление колеса на рельс определяется по формуле
Максимальная величина эквивалентной нагрузки определяется по формуле
где – ординаты линии влияния давлений рельса на шпалы в сечениях пути xi, расположенных под колесными нагрузками на расстоянии xi от осей тележки, смежных с расчетной осью
При расчете координаты средних нагрузок равны x1 = l1, x2 = l2.
Подставив численные значения в приведенные здесь формулы, определим напряжения в элементах верхнего строения пути.
3.13 Определить напряжения сжатия в резиновых прокладках на шпалах σш и в балластном слое под шпалой σб от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если величина эквивалентной нагрузки = 155400 Н, коэффициенте относительной жесткости подрельсового основания и рельса k = 1,38 м -1 , расстояние между осями шпал lш = 0,5 м, площадь прокладки ω = 518·10 -4 м2 и опорная площадь полушпалы Ωα = 2975·10 -4 м2 .
Определить напряжения сжатия в резиновых прокладках на шпалах σш и в балластном слое под шпалой σб от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если величина эквивалентной нагрузки = 178571 Н, коэффициенте относительной жесткости подрельсового основания и рельса k = 1,421 м -1 , расстояние между осями шпал lш = 0,5 м, площадь прокладки ω = 210·10 -4 м2 и опорная площадь полушпалы Ωα = 2975·10 -4 м2 .
Решение задачи
Напряжения смятия в деревянных шпалах под подкладками и в прокладках при железобетонных шпалах определяются по формуле
где Q – давление колеса на рельс;
w – площадь передачи давления на шпалу через подкладку или прокладку (при бесподкладочном скреплении типа ЖБР).
Напряжения в балластном слое под шпалой в подрельсовом сечении определяется по формуле
где 0,5аb – площадь полушпалы (а и b – длина и ширина шпалы);
α – коэффициент изгиба шпалы;
Ωα – эффективная площадь полушпалы с учетом изгиба.
Давление колеса на рельс определяется по формуле
Подставив численные значения в приведенные здесь формулы, определим напряжения в элементах верхнего строения пути.
3.14 Поезд движется по спуску крутизной i = 7 ‰ и по кривой R = 400 м, основное сопротивление движению вагонов ω’’0 = 1,7 Н/кН. Определить суммарное сопротивление движению вагонов.
Поезд движется по спуску крутизной i = 5 ‰ и по кривой R = 500 м, основное сопротивление движению вагонов ω’’0 = 1,7 Н/кН. Определить суммарное сопротивление движению вагонов.
Решение задачи
Суммарное удельное сопротивление движению вагонов в поезде определяется по формуле
Суммарное удельное сопротивление
3.15 Определить поперечную составляющую продольной силы в поезде, действующую наружу кривой R = 500 м, если величина продольной силы в автосцепке N = 700 кН.
Определить поперечную составляющую продольной силы в поезде, действующую наружу кривой R = 600 м, если величина продольной силы в автосцепке N = 600 кН.
Решение задачи
Поперечная составляющая продольной силы в поезде ΔH определяется по формуле
3.16 Определить устойчивость колеса на рельсе в кривой при величине нагрузок от колес на рельсы P = 105 кН, величине рамной силы Ур = 85 кН и величине непогашенного поперечного ускорения αн = 0,25 м/с 2 .
Определить устойчивость колеса на рельсе в кривой при величине нагрузок от колес на рельсы P = 110 кН, величине рамной силы Ур = 80 кН и величине непогашенного поперечного ускорения αн = 0,3 м/с 2 .
Решение задачи
Коэффициент запаса устойчивости колеса на рельсе определяется по формуле
Нагрузки на наружный и внутренний рельсы кривой определяются по формулам
где Q – вес вагона, приходящийся на одну ходовую тележку Q = 4P = 4·110 = 440 кН.
Проверка (126,76+93,24)/2=110 кН.
Подставив полученные значения в первую формулу, получим
В заданных условиях колесо устойчиво на рельсе.
Расчеты бесстыкового пути
3.17 Определить длину концевого участка продольных деформаций рельсовых плетей Р65 при температуре рельсов минус 40 °С и температуре закрепления +25 °С (при нормативной затяжке гаек клеммных и закладных болтов). Стыковое сопротивление 300 кН. Нарисовать эпюру продольных сил.
3.18 Определить величину раскрытия зазора при изломе рельсовой плети Р65 при температуре рельсов –45 °С и температуре закрепления +35 °С (при нормативной затяжке гаек клеммных и закладных болтов). Построить эпюру продольных сил.
3.20 Определить границы интервала закрепления бесстыковой плети при наибольшей температуре рельсов в данной местности tmaxmax = +58 °С, наименьшей tminmin = –54 °С, допускаемое повышение [Δtу] = 45 °С и понижение [Δtр] = 95 °С температуры рельсов.
Расчеты земляного полотна
3.21 Определить ширину основной площадки земляного полотна B и начертить ее схему, для однопутного участка I категории железнодорожной линии в кривой радиусом R = 500 м, грунт земляного полотна – пылеватый песок.
Ширина основной площадки b на прямых однопутных участках, м
| Категория линии | Вид грунта земляного полотна | |
| глинистые, недренирующие мелкие и пылеватые пески | скальные, крупнообломочные с песчаным заполнителем, дренирующие пески | |
| скоростные, особогрузонапряженные, I и II | 7,6 | 6,6 |
| III | 7,3 | 6,4 |
| IV | 7,1 | 6,2 |
Уширение основной площадки Db на кривых участках, м
| Радиус кривой | Уширение |
| 3000 и более 2500-1800 1500-700 600 и менее | 0,2 0,3 0,4 0,5 |
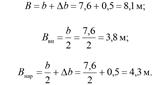
Схема основной площадки земляного полотна
3.22 Назначить крутизну откосов и начертить схему поперечного профиля для насыпи высотой 11 м на однопутном участке, сооружаемой из глинистого грунта со следующими характеристиками: влажность на границе раскатывания Wp = 12 %, влажность на границе текучести WL = 14 %, природная влажность We = 11 %.
Крутизна откосов насыпей

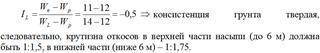
Схема поперечного профиля насыпи
3.23 Определить интенсивность пучения грунта f при следующих значениях влажности грунта: We = 16 %, Wp = 15 %. Рекомендовать способ защиты откосов земляного полотна и определить отметку бермы Гб при следующих исходных данных: ГВВ = 198,4 м, hп = 0,2 м, hн = 1,1 м, DZ = 0,15 м.
Интенсивность пучения f глинистых грунтов в зависимости от влажности в зоне промерзания
Схема к расчету отметки бермы Гб
3.24 Оценить гидравлическую эффективность дренажа, устраиваемого на участке выемки, сложенной грунтами, имеющими условный номер 7в.
Физико-технические характеристики грунта
3.25 Изобразить типовой поперечный профиль щебеночной балластной призмы в кривой на однопутном участке для 1 класса пути. Представить схему с указанием основных размеров.

Форумы

ОАО "РЖД"

Фото

Дневники

Видео

Группы

Файлы

Игры

Объявления

Лента
по наличию или отсутствию выступов (реборд) и направляющих движения крановых конструкций – на одноребордные, двухребордные и безребордные.
При выборе типа колеса крана двухребордные ходовые колеса наиболее применимы. На башенных кранах колеса только двухребордными.
В тележках мостовых кранов, перегрузочных мостов, передвижных кранов с колеей до 4 м можно применять одноребордные ходовые колеса. Эти же колеса применяют для козловых кранов и перегрузочных мостов, каждая сторона которых опирается на два рельсовых пути, при условии, что расположение реборд колес на одном пути будет обратным расположению на противоположной стороне.
Безребордные ходовые колеса применяют в мостовых, консольных кранах, в кранах с поворотным кругом, в поворотных тележках мостовых кранов и т. д. при наличии устройств, исключающих сход колес с рельсов.
При больших пролетах мостовых кранов, опирающихся на четыре ходовых колеса, с целью устранения перекосов моста в качестве ведущих ходовых колес применяют колеса с коническим ободом, установленным большим диаметром внутрь колеи.
Типоразмер ходовых колес определяется их диаметром, который можно принять по таблице в зависимости от максимальной статической нагрузки от веса груза и металлоконструкции крана, приходящихся на одно колесо.
Типоразмер ходовых колес и рельсов
Ходовые колеса кранов входят в состав сборочных единиц “Приводное колесо в сборе” и “Неприводное колесо в сборе”. Эти сборочные единицы называют колесными установками.
В состав колесной установки входит колесо, вал (ось), подшипники, корпусы подшипников (буксы).
по наличию или отсутствию выступов (реборд) и направляющих движения крановых конструкций – на одноребордные, двухребордные и безребордные.
При выборе типа колеса крана двухребордные ходовые колеса наиболее применимы. На башенных кранах колеса только двухребордными.
В тележках мостовых кранов, перегрузочных мостов, передвижных кранов с колеей до 4 м можно применять одноребордные ходовые колеса. Эти же колеса применяют для козловых кранов и перегрузочных мостов, каждая сторона которых опирается на два рельсовых пути, при условии, что расположение реборд колес на одном пути будет обратным расположению на противоположной стороне.
Безребордные ходовые колеса применяют в мостовых, консольных кранах, в кранах с поворотным кругом, в поворотных тележках мостовых кранов и т. д. при наличии устройств, исключающих сход колес с рельсов.
При больших пролетах мостовых кранов, опирающихся на четыре ходовых колеса, с целью устранения перекосов моста в качестве ведущих ходовых колес применяют колеса с коническим ободом, установленным большим диаметром внутрь колеи.
Типоразмер ходовых колес определяется их диаметром, который можно принять по таблице в зависимости от максимальной статической нагрузки от веса груза и металлоконструкции крана, приходящихся на одно колесо.
Типоразмер ходовых колес и рельсов
Ходовые колеса кранов входят в состав сборочных единиц “Приводное колесо в сборе” и “Неприводное колесо в сборе”. Эти сборочные единицы называют колесными установками.
В состав колесной установки входит колесо, вал (ось), подшипники, корпусы подшипников (буксы).
Читайте также:


