Газодинамическая функция q от лямбда
Газодинамическими функциями (приведенными параметрами) называются отношния действительного значения какого- то параметра в произвольном течении потока газа к значению такого же параметра в сравнительном течении.
В качестве сравнительных течений используют критические параметры и параметры торможения. В газодинамике широко используется коэффициент скорости, равный отношению действительной скорости к критической:
Cоотношения между параметрами заторможенного потока и текущими параметрами обозначаются:
Одной из наиболее важных газодинамических функций в теории газодинамики является величина приведенной плотности потока массы газа:
В выражении (19) произведение имеет размерность: и выражение называется плотностью потока массы (удельный расход газа).
Выражение определяет количество газа (кг), протекающее через единицу площади (м 2 ) в единицу времени (с):
, где G (кг/c)- секундный расход потока газа через
сечение площадью F (м 2 ).
Величина 1/q характеризует относительную площадь сечения канала. Действительно, с учетом уравнения неразрывности:
(20) Все приведенные газодинамические функции можно выразить друг через друга.
Затем, зная значения масштабных параметров для приведения, можно числить и действительные параметры для потока газа.
Из (18) видно, что в качестве основного параметра (независимой переменной) принимается коэффициент скорости λ.
Зависимость газодинамических функция от λ для (k=1.4), λmax=2.45 показаны на графике.
Пример расчета сопла Лаваля с использованием газодинамических функций
Определить основные параметры и размеры критического и выходного сечений сопла Лаваля, через которое проходит 2 кг/с газа с параметрами po=1.5 МПа,
To= 2000 o K при истечении в среду рср=0.12 МПа. (Для газа R=400дж/кг К, k=1.4).
По таблицам или по графику находим значения приведенных параметров в критическом сечении (λ=1)
Параметры в выходном сечении найдем, используя исходные данные:
По найденной величине определим:
Тогда параметры потока в выходном сечении соcтавят:
Площадь выходного сечения сопла:
Лекция5
- Особенности распространения слабых возмущений в потоке
Рассмотрим картину распространения слабых возмущений в потоке газа, движущимся с различными скоростями.
Источником возмущения может служить точечное тело или острие тонкого предмета, на которое набегает поток газа.
В это случае от источника возмущения, находящегося в точке Ао, будут распространяться сферические волны со скоростью с=a;
Через некоторый промежуток времени : t, 2t, 3t возмущения достигают точек, расположенных на сферических поверхностях: at; a2t; a3t.
Через достаточно большой промежуток времени возмущение распространится на весь объем, занимаемый газом.

В этом случае каждая определенная волна возмущения также является сферической, но точки, которых достигло возмущение, сносятся потоком со скоростью, равной с, вправо.
Центр каждой волны смещается вправо с той же скоростью и в моменты времени: t,2t, 3t.
и т.д. находятся на расстоянии сt; 2ct; 3ct. Как и в предыдущем случае, любая волна через достаточно большой промежуток времени распределяется на весь объем газа, толко навстречу потоку возмущения распространяются со скоростью с-a, а по потоку со скоростью с+a.
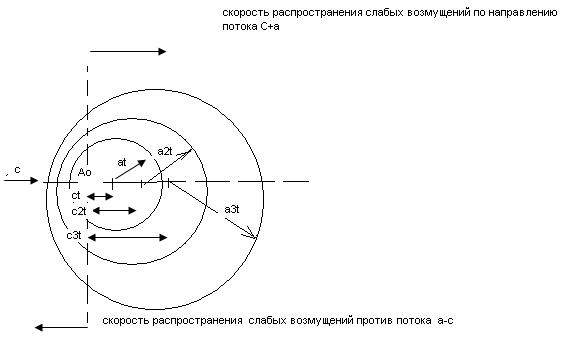
- скорость газа равна скорости звука (с=a)
В этом случае сферическая волна возмущения сносится потоком на величину своего размера и источник возмущения всегда находится на фронте волны.
С течением времени возмущения распространяются в газе, но они никогда не могут проникнуть в область, находящуюся перед источником возмущения, т.е. левее линии АОВ.

Cкорость газа больше скорости звука с>a
Область, куда могут проникнуть возмущения, становится меньше, чем в предыдущем случае. Она имеет вид конуса с вершиной в точке источника возмущения, описанного около сферических поверхностей.
Ясно, что в точки, расположенные за пределами этой сферической поверхности, возмущения никогда не попадут.Область, в которую проникают возмущения от точечных источников, движущихся в газе со сверхзвуковой скоростью, называется конусом Маха.
Угол называется углом возмущений.
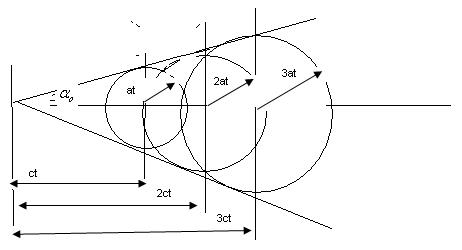
Если скорость потока газа меньше скорости звука, то возмущения распространяются во всех объемах газа в том числе и в областях, находящихся перед источником возмущения.
Поток “ чувствует” находящееся впереди него препятствие задолго до приближении к нему и поэтому заранее перестраивается в зависимости от характера препятствия.
Если скорость потока равна скорости звука или большее ее, то возмущение, возникающее
от неподвижных предметов, не может проникнуть навстречу потоку.
До тех пор, пока частица газа не пересечет поверхность конца возмущений, возмущение, создающее этот конус, никак не влияет на движение частицы. Поэтому при движении со сверхзвуковой скоростью поток частиц подходит к препятствию неподготовленным- он не “ чуствует “ препятствия, расположенного впереди.
Невозможность предварительной перестройки (подготовки) потока при подходе к
препятствию является главной особенностью сверхзвукового потока и в этом случае в потоке образуется поверхность разрыва.
При пересечении потоком поверхности разрыва давление, температура и плотность возрастают, а скорость падает. Причем эти изменения происходят резко, скачком.
Поверхность разрыва, перемещающаяся в пространстве, называется ударной волной, а неподвижную ударную волну- скачком уплотнения.
Скачок уплотнения- зона резкого возрастания давления и плотности газа в сверхзвуковом потоке.
Скачок уплотнения сопровождается возрастанием давления, плотности, температуры, уменьшением скорости и чисел М и λ.
Существуют прямой и косой скачки уплотнений.
Прямой скачок- фронт скачка уплотнения перпендикулярен вектору скорости потока.
Уравнение энергии для прямого скачка примет вид:
С1, T1 – cкорость и температура потока газа до скачка уплотнения;
С2, T2 – cкорость и температура потока газа после скачка уплотнения;
Используя уравнения неразрывности и изменения количества движения, можно получить выражения для прямого скачка:
Из (1) видно, что в прямом скачке уплотнения сверхзвуковая скорость газа переходит в дозвуковую и чем выше скорость до скачка, тем сильнее скачок. С уменьшением начальной скорости с1 скачок ослабевает и исчезает совсем при .
Давление и плотность газа до и после скачка уплотнения связаны соотношениям
называемым уравнением ударной адиабаты:
Для прямого скачка:
Cущественной особенностью параметров потока газа при сверхзвуковом течении является то, что при неограниченном возрастании давления в скачке уплотнения ( отношение температур и давлений возрастают безгранично, а отношение плотностей имеет определенный предел, значение которого определяется выражением:
Косой скачок- фронт скачка уплотнения расположен по углом, отличном от 90 о к вектору скорости потока. Скорость С1- до косого скачка и С2- после косого скачка можно представить составляющими- нормальными к плоскости скачка Cn1 и Cn2 и касательными к ней: Ct1 и Сt2.
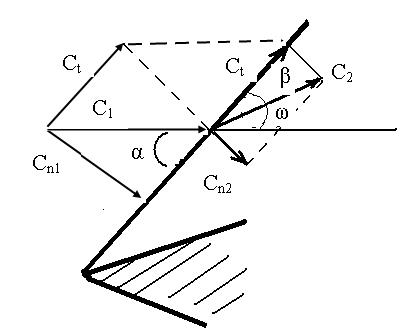
С1- вектор скорости потока перед скачком уплотнения
С2- вектор скорости потока после скачка уплотнения
α- угол наклона фронта скачка к вектору скорости невозмущенного потока
ω- угол поворота вектора скорости после скачка уплотнения
- угол между вектором скорости и фронтом скачка
Основная задача о косом скачке- установление связи между параметрами до и после скачка и определение потерь , возникающих при переходе через скачок.
Используя закон сохранения массы- уравнение неразрывности, получим:
Используя закон сохранения импульсов- уравнение изменения количества движения, получим:
- касательные составляющие скоростей до и после скачка уплотнения одинаковы.
Используя закон сохранения энергии- уравнение Бернулли, можно найти взаимосвязь скоростей до и после скачка уплотнения:
Из уравнений сохранения можно получить выражения, связывающие между собой определенные параметры (например, статическое и заторможенное давления) в одном и том же сечении через число Маха или приведенную скорость и показатель адиабаты. Эти выражения получили название газодинамических функций.
Расчет газовых потоков с помощью газодинамических функций получил широкое распространение и является общепринятым.
Газодинамическим функциям присвоены следующие обозначения:
| отношение статического давления к заторможенному | ; |
| отношение статической температуры к заторможенной | |
| отношение статической плотности к заторможенной | ; |
| отношение плотности тока к максимальному значению плотности тока, соответствующему течению со скоростью звука | . |
Кроме перечисленных функций используются и другие функции, одна из которых равна отношению функций q(M) и p(M):
Формулы для расхода газа в некотором сечении через параметры газа и газодинамические функции имеют вид
Для воздуха (g = 1,4, R = 287,3 Дж/(кг×К)) коэффициент m = 0,0404 с×К 0,5 /м.
Определить расход воздуха из отверстия площадью Fот = 5 см 2 в стенке сосуда, а также температуру и давление воздуха в этом отверстии, если температура и давление в сосуде поддерживаются постоянными и равными соответственно Тс = 500 К и рс = 0,15 МПа. Давление окружающей среды р0 = 0,1 МПа. Потери не учитывать.
Определим значение газодинамической функции p(М), предполагая, что давление в отверстии равно р0.
По таблицам газодинамических функций для g = 1,4 (приложение 2) находим число Маха в отверстии Мот = 0,78. Поскольку
Мот
Задача 2.5.6. Температура воздуха в баке большого объема равна
500 К. Температура струи воздуха, вытекающего из бака равна 400 К. Какова скорость потока и число Маха в струе?
Задача 2.5.7. Воздух вытекает из бака через суживающееся сопло. В баке поддерживается постоянное давление рб = 0,18 МПа, а скорость газа в нем можно считать пренебрежимо малой. Определить давление в выходном сечении сопла в двух случаях: давление в пространстве за соплом равно 0,12 МПа и 0,08 МПа.
Задача 2.5.8. Параметры изоэнтропийного торможения воздуха перед суживающимся соплом равны: давление – 0,1 МПа; температура – 600 К. Определить критический расход воздуха через сопло, если площадь его минимального сечения составляет 25×10 -4 м2 .
Задача 2.5.9. Воздух течет из бака через суживающееся сопло, причем течение можно рассматривать как изоэнтропийное одномерное. Отношение давлений в пространстве за соплом и в баке равно 0,8. Во сколько раз нужно повысить давление в баке, чтобы расход через сопло увеличился в 1,3 раза при условии, что температура воздуха в баке и давление за соплом неизменны?
Задача 2.5.10. Воздух из левого резервуара течет в правый через суживающееся сопло 1, а из него вытекает в атмосферу через суживающееся сопло 2 (рис. 2.19). Струя, выходящая из сопла 1, полностью тормозится в правом резервуаре. Резервуары теплоизолированы. Давление в левом резервуаре можно произвольно изменять с помощью дросселя 3 на трубопроводе, по которому подается сжатый воздух. Выходные площади сопел равны. Атмосферное давление равно 0,1 МПа. При каком условии расход воздуха через систему пропорционален давлению воздуха в левом резервуаре?
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.004)
Газодинамическими функциями (приведенными параметрами) называются отношния действительного значения какого- то параметра в произвольном течении потока газа к значению такого же параметра в сравнительном течении.
В качестве сравнительных течений используют критические параметры и параметры торможения. В газодинамике широко используется коэффициент скорости, равный отношению действительной скорости к критической:
Cоотношения между параметрами заторможенного потока и текущими параметрами обозначаются:
Одной из наиболее важных газодинамических функций в теории газодинамики является величина приведенной плотности потока массы газа:
В выражении (19) произведение имеет размерность: и выражение называется плотностью потока массы (удельный расход газа).
Выражение определяет количество газа (кг), протекающее через единицу площади (м 2 ) в единицу времени (с):
, где G (кг/c)- секундный расход потока газа через
сечение площадью F (м 2 ).
Величина 1/q характеризует относительную площадь сечения канала. Действительно, с учетом уравнения неразрывности:
(20) Все приведенные газодинамические функции можно выразить друг через друга.
Затем, зная значения масштабных параметров для приведения, можно числить и действительные параметры для потока газа.
Из (18) видно, что в качестве основного параметра (независимой переменной) принимается коэффициент скорости λ.
Зависимость газодинамических функция от λ для (k=1.4), λmax=2.45 показаны на графике.
Пример расчета сопла Лаваля с использованием газодинамических функций
Определить основные параметры и размеры критического и выходного сечений сопла Лаваля, через которое проходит 2 кг/с газа с параметрами po=1.5 МПа,
To= 2000 o K при истечении в среду рср=0.12 МПа. (Для газа R=400дж/кг К, k=1.4).
По таблицам или по графику находим значения приведенных параметров в критическом сечении (λ=1)
Параметры в выходном сечении найдем, используя исходные данные:
По найденной величине определим:
Тогда параметры потока в выходном сечении соcтавят:
Площадь выходного сечения сопла:
Лекция5
- Особенности распространения слабых возмущений в потоке
Рассмотрим картину распространения слабых возмущений в потоке газа, движущимся с различными скоростями.
Источником возмущения может служить точечное тело или острие тонкого предмета, на которое набегает поток газа.
В это случае от источника возмущения, находящегося в точке Ао, будут распространяться сферические волны со скоростью с=a;
Через некоторый промежуток времени : t, 2t, 3t возмущения достигают точек, расположенных на сферических поверхностях: at; a2t; a3t.
Через достаточно большой промежуток времени возмущение распространится на весь объем, занимаемый газом.

В этом случае каждая определенная волна возмущения также является сферической, но точки, которых достигло возмущение, сносятся потоком со скоростью, равной с, вправо.
Центр каждой волны смещается вправо с той же скоростью и в моменты времени: t,2t, 3t.
и т.д. находятся на расстоянии сt; 2ct; 3ct. Как и в предыдущем случае, любая волна через достаточно большой промежуток времени распределяется на весь объем газа, толко навстречу потоку возмущения распространяются со скоростью с-a, а по потоку со скоростью с+a.

- скорость газа равна скорости звука (с=a)
В этом случае сферическая волна возмущения сносится потоком на величину своего размера и источник возмущения всегда находится на фронте волны.
С течением времени возмущения распространяются в газе, но они никогда не могут проникнуть в область, находящуюся перед источником возмущения, т.е. левее линии АОВ.

Cкорость газа больше скорости звука с>a
Область, куда могут проникнуть возмущения, становится меньше, чем в предыдущем случае. Она имеет вид конуса с вершиной в точке источника возмущения, описанного около сферических поверхностей.
Ясно, что в точки, расположенные за пределами этой сферической поверхности, возмущения никогда не попадут.Область, в которую проникают возмущения от точечных источников, движущихся в газе со сверхзвуковой скоростью, называется конусом Маха.
Угол называется углом возмущений.

Если скорость потока газа меньше скорости звука, то возмущения распространяются во всех объемах газа в том числе и в областях, находящихся перед источником возмущения.
Поток “ чувствует” находящееся впереди него препятствие задолго до приближении к нему и поэтому заранее перестраивается в зависимости от характера препятствия.
Если скорость потока равна скорости звука или большее ее, то возмущение, возникающее
от неподвижных предметов, не может проникнуть навстречу потоку.
До тех пор, пока частица газа не пересечет поверхность конца возмущений, возмущение, создающее этот конус, никак не влияет на движение частицы. Поэтому при движении со сверхзвуковой скоростью поток частиц подходит к препятствию неподготовленным- он не “ чуствует “ препятствия, расположенного впереди.
Невозможность предварительной перестройки (подготовки) потока при подходе к
препятствию является главной особенностью сверхзвукового потока и в этом случае в потоке образуется поверхность разрыва.
При пересечении потоком поверхности разрыва давление, температура и плотность возрастают, а скорость падает. Причем эти изменения происходят резко, скачком.
Поверхность разрыва, перемещающаяся в пространстве, называется ударной волной, а неподвижную ударную волну- скачком уплотнения.
Скачок уплотнения- зона резкого возрастания давления и плотности газа в сверхзвуковом потоке.
Скачок уплотнения сопровождается возрастанием давления, плотности, температуры, уменьшением скорости и чисел М и λ.
Существуют прямой и косой скачки уплотнений.
Прямой скачок- фронт скачка уплотнения перпендикулярен вектору скорости потока.
Уравнение энергии для прямого скачка примет вид:
С1, T1 – cкорость и температура потока газа до скачка уплотнения;
С2, T2 – cкорость и температура потока газа после скачка уплотнения;
Используя уравнения неразрывности и изменения количества движения, можно получить выражения для прямого скачка:
Из (1) видно, что в прямом скачке уплотнения сверхзвуковая скорость газа переходит в дозвуковую и чем выше скорость до скачка, тем сильнее скачок. С уменьшением начальной скорости с1 скачок ослабевает и исчезает совсем при .
Давление и плотность газа до и после скачка уплотнения связаны соотношениям
называемым уравнением ударной адиабаты:
Для прямого скачка:
Cущественной особенностью параметров потока газа при сверхзвуковом течении является то, что при неограниченном возрастании давления в скачке уплотнения ( отношение температур и давлений возрастают безгранично, а отношение плотностей имеет определенный предел, значение которого определяется выражением:
Косой скачок- фронт скачка уплотнения расположен по углом, отличном от 90 о к вектору скорости потока. Скорость С1- до косого скачка и С2- после косого скачка можно представить составляющими- нормальными к плоскости скачка Cn1 и Cn2 и касательными к ней: Ct1 и Сt2.

С1- вектор скорости потока перед скачком уплотнения
С2- вектор скорости потока после скачка уплотнения
α- угол наклона фронта скачка к вектору скорости невозмущенного потока
ω- угол поворота вектора скорости после скачка уплотнения
- угол между вектором скорости и фронтом скачка
Основная задача о косом скачке- установление связи между параметрами до и после скачка и определение потерь , возникающих при переходе через скачок.
Используя закон сохранения массы- уравнение неразрывности, получим:
Используя закон сохранения импульсов- уравнение изменения количества движения, получим:
- касательные составляющие скоростей до и после скачка уплотнения одинаковы.
Используя закон сохранения энергии- уравнение Бернулли, можно найти взаимосвязь скоростей до и после скачка уплотнения:
а) Газодинамические функции. Расчеты течений газа в элементах авиационных силовых установок являются сложной задачей, так как требует учета одновременного изменения скорости, температуры, давления и плотности газа. Эта задача может быть упрощена, если проводить такие расчеты с использованием газодинамических функций, представляющих собой зависимости ряда безразмерных параметров газового потока от приведенной скорости . К ним относятся следующие функции.
Функция t(l) - это отношение статической температуры газового потока при данном значении l к температуре адиабатно заторможенного потока, т.е. .
Подставив в формулу для выражение, связывающее числа М и , и сделав ряд алгебраических преобразований, получим
Функция П(l) - это отношение статического давления газового потока при данном значении l к давлению адиабатно заторможенного потока.
Используя соотношение параметров в адиабатном процессе, получим
Функция e(l) - это отношение статической плотности газового потока при данном значении l к плотности адиабатно заторможенного потока:
Эти три функции характеризуют изменение параметров состояния газа при изменении l в энергоизолированном потоке. На рис. 4.12а показан характер их зависимокти от l при различных значениях показателя адиабаты. При l = 0 эти функции равны единице, а при l ® l пред стремятся к нулю.
Функция q(l) - относительная плотность тока,- это отношение плотности тока в потоке газа при данной величине l к её значению , которое достигается (при данных параметрах заторможенного потока) при скорости газа, равной скорости звука (т.е. при значении l=1).
Учитывая, что , , а ,получим
Как видно из рис. 4.12б, максимальное значение , равное единице, достигается при l = 1. Это означает, что в энергоизолированом потоке максимальная плотность тока достигается тогда, когда скорость потока становится равной скорости звука.
Читайте также:

