В данных изображениях определи вид симметрии осевая центральная или обе знак мерседеса
Доступно для всех учеников 1-11 классов и дошкольников
секция: естественно - научная
ВИДЫ СИММЕТРИИ
Руководитель: учитель математики высшей
категории Мочалыгина Ирина Анатольевна
Структура проекта:
2. Цели и задачи проекта.
3. Виды симметрии :
3.1. Центральная симметрия;
3.2. Осевая симметрия;
3.3. Зеркальная симметрия (симметрия относительно плоскости);
3.4. Поворотная симметрия;
3.5. Переносная симметрия.
Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.
Цель работы : Знакомство с различными видами симметрии.
Задачи:
Изучить литературу по данному вопросу.
Обобщить и систематизировать изученный материал.
Существуют две группы симметрий.
К первой группе относится симметрия положений, форм, структур. Это та симметрия, которую можно непосредственно видеть. Она может быть названа геометрической симметрией.
Вторая группа характеризует симметрию физических явлений и законов природы. Эта симметрия лежит в самой основе естественнонаучной картины мира: ее можно назвать физической симметрией.
Я остановлюсь на изучении геометрической симметрии .
В свою очередь, геометрической симметрии существует тоже несколько видов: центральная, осевая, зеркальная (симметрия относительно плоскости) радиальная (или поворотная), переносная и другие. Я рассмотрю сегодня 5 видов симметрии.
Центральная симметрия
Две точки А и А 1 называются симметричными относительно точки О, если они лежат на прямой, проходящей через т О и находятся по разные стороны от неё на одинаковом расстоянии. Точка О называется центром симметрии.

Фигура называется симметричной относительно точки О , если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры, говорят, что фигура обладает центральной симметрией.

Примерами фигур, обладающими центральной симметрией является окружность и параллелограмм.
Фигуры, изображённые на слайде симметричны, относительно некоторой точки
2. Осевая симметрия
Две точки X и Y называются симметричными относительно прямой t , если эта прямая проходит чрез середину отрезка ХУ и перпендикулярна к нему. Также следует сказать, что каждая точка прямой t считается симметричной сама себе.
Прямая t – ось симметрии.
Фигура называется симметричной относительно прямой t , если для каждой точки фигуры симметричная ей точка относительно прямой t также принадлежит этой фигуре.
Прямая t называется осью симметрии фигуры, говорят, что фигура обладает осевой симметрией.

Осевой симметрией обладают неразвёрнутый угол , равнобедренный и равносторонний треугольники, прямоугольник и ромб, буквы (смотри презентацию).

Зеркальная симметрия (симметрия относительно плоскости)
Две точки Р 1 и Р называются симметричными относительно плоскости а если они лежат на прямой, перпендикулярной плоскости а, и находятся от неё на одинаковом расстоянии
Зеркальная симметрия хорошо знакома каждому человеку. Она связывает любой предмет и его отражение в плоском зеркале. Говорят, что одна фигура зеркально симметрична другой.
На плоскости фигурой с бесчисленным множеством осей симметрии был круг. В пространстве бесчисленное множество плоскостей симметрии имеет шар.
Но если круг является единственным в своем роде, то в трехмерном мире имеется целый ряд тел, обладающих бесконечным множеством плоскостей симметрии: прямой цилиндр с кругом в основании, конус с круговым основанием, шар.
Легко установить, что каждая симметричная плоская фигура может быть с помощью зеркала совмещена сама с собой. Достойно удивления, что такие сложные фигуры, как пятиконечная звезда или равносторонний пятиугольник, тоже симметричны. Как это вытекает из числа осей, они отличаются именно высокой симметрией. И наоборот: не так просто понять, почему такая, казалось бы, правильная фигура, как косоугольный параллелограмм, несимметрична.

4. П оворотная симметрия (или радиальная симметрия)
Поворотная симметрия — это симметрия, сохраняющаяся форму предмета при повороте вокруг некоторой оси на угол, равный 360°/ n (или кратный этой величине), где n = 2, 3, 4, … Указанную ось называют поворотной осью n -го порядка.



При п=2 все точки фигуры поворачиваются на угол 180 0 ( 360 0 /2 = 180 0 )вокруг оси, при этом форма фигуры сохраняется, т.е. каждая точка фигуры переходит в точку той же фигуры(фигура преобразуется сама в себя). Ось называют осью второго порядка.
На рисунке 2 показана ось третьего порядка, на рисунке 3 – 4 порядка, на рисунке 4 - 5-го порядка.
Предмет может иметь более одной поворотной оси: рис.1 – 3оси поворота, рис.2 -4 оси, рис 3 – 5 осей, рис. 4 – только 1 ось
Кроме того буква и имеет центр симметрии, а буква Ф ось симметрии
Вернемся к примерам из жизни: стакан, конусообразный фунтик с мороженым, кусочек проволоки, труба.
Если мы повнимательней присмотримся к этим телам, то заметим, что все они, так или иначе состоят из круга, через бесконечное множество осей симметрии которого проходит бесчисленное множество плоскостей симметрии. Большинство таких тел (их называют телами вращения) имеют, конечно, и центр симметрии (центр круга), через который проходит по меньшей мере одна поворотная, ось симметрии.
Отчетливо видна, например, ось у конуса фунтика с мороженым. Она проходит от середины круга (торчит из мороженого!) до острого конца конуса-фунтика. Совокупность элементов симметрии какого-либо тела мы воспринимаем как своего рода меру симметрии. Шар, без сомнения, в отношении симметрии является непревзойденным воплощением совершенства, идеалом. Древние греки воспринимали его как наиболее совершенное тело, а круг, естественно, как наиболее совершенную плоскую фигуру.
Для описания симметрии конкретного объекта надо указать все поворотные оси и их порядок, а также все плоскости симметрии.
Рассмотрим, например, геометрическое тело, составленное из двух одинаковых правильных четырехугольных пирамид.
Оно имеет одну поворотную ось 4-го порядка (ось АВ), четыре поворотные оси 2-го порядка (оси СЕ, DF , MP , NQ ), пять плоскостей симметрии (плоскости CDEF , AFBD , ACBE , AMBP , ANBQ ).
5 . Переносная симметрия
Ещё одним видом симметрии является переносная с имметрия.

а
Периодически повторяющийся рисунок на длинной ленте называется бордюром. На практике бордюры встречаются в различных видах (настенная роспись, чугунное литье, гипсовые барельефы или керамика). Бордюры применяют маляры и художники при оформлении комнаты. Для выполнения этих орнаментов изготавливают трафарет. Передвигаем трафарет, переворачивая или не переворачивая его, обводим контур, повторяя рисунок, и получается орнамент (наглядная демонстрация).
Бордюр легко построить с помощью трафарета (исходного элемента), сдвигая или переворачивая его и повторяя рисунок. На рисунке изображены трафареты пяти видов: а ) несимметричный; б, в ) имеющие одну ось симметрии: горизонтальную или вертикальную; г ) центрально-симметричный; д ) имеющий две оси симметрии: вертикальную и горизонтальную.
Для построения бордюров используют следующие преобразования:
а ) параллельный перенос; б ) симметрию относительно вертикальной оси; в ) центральную симметрию; г ) симметрию относительно горизонтальной оси.
Аналогично можно построить розетки. Для этого круг делят на n равных секторов, в одном из них выполняют образец рисунка и затем последовательно повторяют последний в остальных частях круга, поворачивая рисунок каждый раз на угол 360°/ n .
Наглядным примером применения осевой и переносной симметрии может служить забор, изображённый на фотографии.

Вывод: Таким образом, существуют различные виды симметрии, симметричные точки в каждом из этих видов симметрии строятся по определённым законам. В жизни мы повсюду встречаемся тем или иным видом симметрии, а часто у предметов, которые нас окружают, можно отметить сразу несколько видов симметрии. Это создаёт порядок, красоту и совершенство в окружающем нас мире.
Современный словарь иностранных слов. — М.: Русский язык, 1993г .

Здравствуйте, помогите решить нестандартную задачу, это задали в 6 классе человеку, кумуляту даже в вузе не изучали в России, есть пара вариантов реше … ния, но может кто-то знает как это решать? По переводу примерно следующее: кумулятивная частота показывает количество часов, которое группа людей проводит за рулем каждую неделю. Найти среднее кол-во часов вождения по ответам внизу
Задача про скидку Марина выбрала в магазине юбку за 1000 р и футболку за 800 р. На кассе она узнала, что сегодня на всю одежду скидка 20%. Сколько руб … лей составит стоимость покупки с учётом скидки?
Помогите пжпж!! ДАМ 55 БАЛЛОВ! Какие числа надо вписать в окошки, чтобы равенство стало верным? Запишите в ответ цифры без запятых, пробелов и других … дополнительных символов. дробь: числитель: 2, знаменатель: 7 конец дроби плюс дробь: числитель: 3, знаменатель: 7 конец дроби = дробь: числитель: ?, знаменатель: ? конец дроби . Ответ: 2 Задание 2 Какое число нужно написать в числителе, чтобы равенство стало верным? дробь: числитель: 8, знаменатель: 36 конец дроби = дробь: числитель: ?, знаменатель: 9 конец дроби $ Ответ: 3 Задание 2 Какое число нужно написать в числителе, чтобы равенство стало верным? дробь: числитель: 9, знаменатель: 27 конец дроби = дробь: числитель: ?, знаменатель: 3 конец дроби Ответ: 4 Задание 2 Какое число нужно написать в числителе, чтобы равенство стало верным? дробь: числитель: 14, знаменатель: 63 конец дроби = дробь: числитель: ?, знаменатель: 9 конец дроби Ответ: 5 Задание 2 Какое число нужно написать в числителе, чтобы равенство стало верным? дробь: числитель: 10, знаменатель: 25 конец дроби = дробь: числитель: ?, знаменатель: 5 конец дроби Ответ: 6 Задание 2 Сколько минут в дробь: числитель: 1, знаменатель: 10 конец дроби ч? Ответ: 7 Задание 2 Сколько минут в дробь: числитель: 3, знаменатель: 4 конец дроби ч? Ответ: 8 Задание 2 Сложите дробь: числитель: 2, знаменатель: 5 конец дроби числа 40 и дробь: числитель: 2, знаменатель: 3 конец дроби числа 60. В ответе напишите полученный результат. Ответ: 9 Задание 2 Из дробь: числитель: 5, знаменатель: 6 конец дроби числа 72 вычтите дробь: числитель: 2, знаменатель: 9 конец дроби числа 81. В ответе напишите полученный результат. Ответ: 10 Задание 2 Треть числа равна 27. Найдите это число. Ответ: 11 Задание 2 Три четверти числа равны 60. Найдите это число. Ответ: 12 Задание 2 Сколько минут в дробь: числитель: 2, знаменатель: 5 конец дроби ч? В ответе укажите только число. Ответ: 13 Задание 2 Сложите дробь: числитель: 3, знаменатель: 5 конец дроби числа 20 и дробь: числитель: 1, знаменатель: 6 конец дроби числа 18. В ответе напишите полученный результат. Ответ: 14 Задание 2 Из дробь: числитель: 4, знаменатель: 7 конец дроби числа 56 вычтите дробь: числитель: 3, знаменатель: 11 конец дроби числа 33. В ответе напишите полученный результат. Ответ: 15 Задание 2 Представьте число 4 в виде дроби со знаменателем 7. Ответ: 16 Задание 2 Представьте число 3 в виде дроби с числителем 21. Ответ: 17 Задание 2 Даны четыре числа: 1 дробь: числитель: 5, знаменатель: 16 конец дроби ; дробь: числитель: 21, знаменатель: 11 конец дроби ; дробь: числитель: 19, знаменатель: 16 конец дроби ; 1 дробь: числитель: 8, знаменатель: 11 конец дроби . Запишите в ответ самое большое из данных чисел. Ответ: 18 Задание 2 Даны четыре числа: 1 дробь: числитель: 8, знаменатель: 17 конец дроби ; дробь: числитель: 20, знаменатель: 17 конец дроби ; дробь: числитель: 25, знаменатель: 13 конец дроби ; 1 дробь: числитель: 7, знаменатель: 13 конец дроби . Запишите в ответ самое большое из данных чисел. Ответ: 19 Задание 2 Представьте в виде смешанного числа выражение дробь: числитель: 17, знаменатель: 7 конец дроби плюс дробь: числитель: 6, знаменатель: 7 конец дроби . Ответ: 20 Задание 2 Представьте в виде смешанного числа выражение дробь: числитель: 37, знаменатель: 9 конец дроби плюс дробь: числитель: 12, знаменатель: 9 конец дроби . Ответ: 21 Задание 2 Представьте в виде смешанного числа выражение дробь: числитель: 45, знаменатель: 7 конец дроби минус дробь: числитель: 26, знаменатель: 7 конец дроби . Ответ: 22 Задание 2 Найдите значение выражения дробь: числитель: 58, знаменатель: 9 конец дроби минус дробь: числитель: 4, знаменатель: 9 конец дроби . Ответ: 23 Задание 2 Представьте число 4 в виде дроби со знаменателем 6. Ответ: 24 Задание 2 Представьте число 5 в виде дроби с числителем 35. Ответ: 25 Задание 2 Представьте в виде смешанного числа выражение дробь: числитель: 27, знаменатель: 7 конец дроби минус дробь: числитель: 8, знаменатель: 7 конец дроби . Ответ: 26 Задание 2 Представьте в виде смешанного числа выражение дробь: числитель: 45, знаменатель: 7 конец дроби минус дробь: числитель: 26, знаменатель: 7 конец дроби . Ответ: 27 Задание 2 Представьте число 8 в виде дроби со знаменателем 6. Ответ: 28 Задание 2 Запишите число 9 в виде дроби со знаменателем 7. Ответ: 29 Задание 2 Представьте в виде неправильной дроби число 2 дробь: числитель: 3, знаменатель: 7 конец дроби . Ответ: 30 Задание 2 Найдите значение выражения дробь: числитель: 47, знаменатель: 9 конец дроби минус дробь: числитель: 2, знаменатель: 9 конец дроби . Ответ:
Найдите наименьшее пятизначное число, которое делится на 45, а все цифры этого числа являются чётными.
Перевозили некоторое количество контейнеров двух типов; масса каждого контейнера первого типа составляла 0,4 т, а масса каждого контейнера второго тип … а составляла 0,7 т. Общий вес всех контейнеров составил 6 т. Найдите возможное количество контейнеров каждого типа, составив систему уравнений и решив ее!
в одной школе есть 750 учеников,495 из этих все хорошо сдали материалы.какой процент студентов сдали хорошо все материалы.?
Центральная симметрия – самая интересная и познавательная тема в геометрии, которую изучают в начальных классах школы и более тщательно — в 8 — 11 классах. Знания по этой теме обязательно пригодятся ученику в жизни.
Что такое центральная симметрия
Начнём с определения: центральная симметрия - одно из свойств определённой геометрической фигуры, при котором точке В соответствует некая точка В1, находящая в таком же пространственном положении относительно точки С. Точка С лежит на середине отрезка ВВ1. Точка С называется центром симметрии. Это определение соответствует курсу планиметрии.
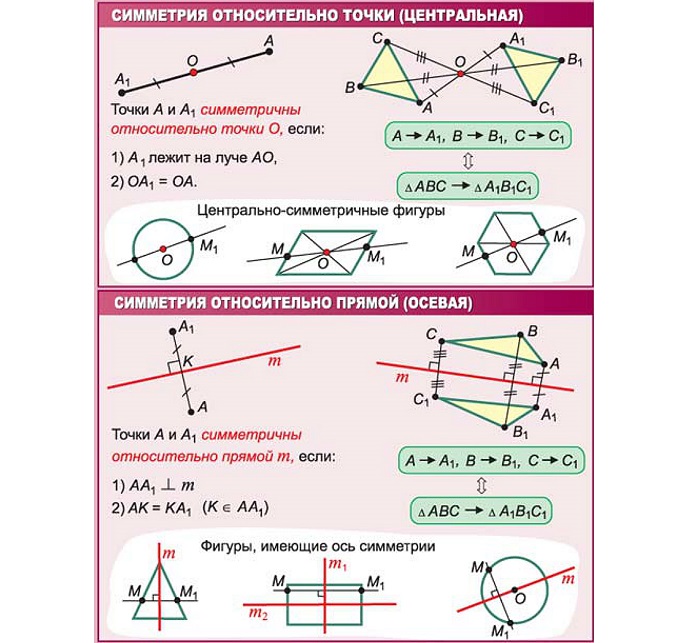
Центральную симметрию можно построить и в пространстве. В пространстве центральной симметрией называется словно зеркальное отображение какой-либо геометрической фигуры. Она представляет собой две одинаковые фигуры, соответственные точки которых попарно симметричны относительно точки пространства О.
Свойства центральной симметрии
Основные свойства следующие:
1. Центральную симметрию называют движением, при котором соответствующие точки также остаются симметричными, то есть расстояние между ними остаётся прежним.
Посмотрим на рисунок. Треугольники АВС и А1В1С1 симметричны в пространстве относительно точки О. При каком либо преобразовании пространства сохраняются условия: АО=А1О, ВО=В1О, СО=С1О. Значит, картинка остаётся той же.

Однако если представить геометрическую фигуру в виде векторов, то при преобразовании пространства эти векторы поменяют свои направления;
2. Центральная симметрия имеет только одну центральную точку, которая является неподвижной при преобразовании пространства;
3. Если прямая проходит через центр симметрии, то она соответствует самой себе, то есть симметрична;
4. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.
Доказывается это свойство достаточно просто. Для этого нужно построить две параллельные прямые АВ и А1В1 относительно точки О.
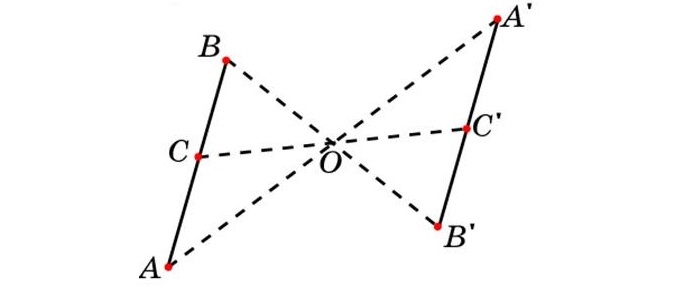
Далее соединяем симметричные точки и получаем отрезки АА1 и ВВ1. Далее легко заметить, что отрезки АО и А1О будут равны. Соответственно равны и отрезки ВО и В1О. Углы, которые образуются при пересечении двумя прямыми точки О также равны.
Значит, треугольники равны по двум сторонам и углу между ними. Следовательно, равны углы А,А1 и В,В1. Значит они являются накрест лежащими при секущих АА1 и ВВ1. Задача решена, АВ и А1В1 параллельны;
5. При центральной симметрии отрезки симметричны отрезкам, лучи симметричны лучам, прямые симметричны прямым.
Примеры фигур, обладающих центральной симметрией
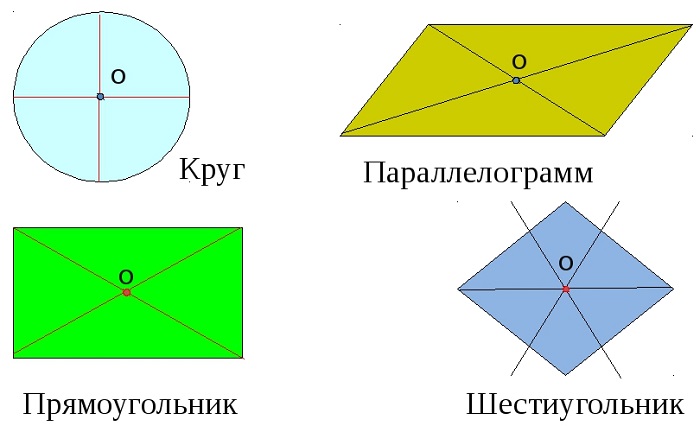
Фигур, как имеющих углы, так и без углов, но при этом обладающих центральной симметрией не так уж мало:
различные правильные многоугольники.
Интересные факты о центральной симметрии
Вся окружающая нас природа – сплошная центральная симметрия. Многие растения и насекомые обладают центральной симметрией.

Практически у каждого фрукта есть своя симметрия. Например, кокос в разрезе представляет собой окружность с центром в некоторой точке.
Ещё один очевидный пример – бабочка.

Великолепные узоры на её крылышках – четкая и яркая симметрия.
Каждый знает, что видовое разнообразие морских ракушек бесконечно. Наверняка, вы сможете найти несколько как с осевой, так и центральной симметрией.
Великолепные примеры с элементами центральной симметрии можно наблюдать и в архитектуре. Потолки различных храмов и церквей украшаются орнаментами, основой которых является центральная симметрия.

Собор Парижской Богоматери имеет прекрасный, утончённый узор, основанный на центральной симметрии.
Рукодельницы в своих произведениях искусства применяют симметрию, которая заметна в удивительных и затейливых узорах.
Таким образом, центральная симметрия – основа, которая составляет природу, архитектуру и даже иногда музыку. Именно это проявление так радует человеческий глаз при появлении первых снежинок или при знакомстве с сооружениями архитектуры.

Осевая и центральная симметрия — тема для перфекционистов, любителей снимков в отражении и противников заваленного горизонта. Симметрично — значит красиво? Тогда давайте разберемся, что такое симметрия с точки зрения математики.
О чем эта статья:
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
На рисунках осевая симметрия: точки A и B симметричны относительно прямой a; точки R и F симметричны относительно прямой AB
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.

Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Читайте также:

