Показательное распределение с параметром лямбда
В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.
Каталог формул по теории вероятности онлайн
Законы распределения на этой странице
Дискретные случайные величины
Биномиальное распределение ДСВ
Пусть дискретная случайная величина $X$ - количество "успехов" в последовательности из $n$ независимых случайных экспериментов, таких что вероятность "успеха" в каждом из них равна $p$ ("неуспеха" - $q=1-p$).
Закон распределения $X$ имеет вид:
| $x_k$ | 0 | 1 | . | k | . | n |
| $p_k$ | $q^n$ | $n\cdot p \cdot q^$ | $C_n^k \cdot p^k \cdot q^$ | $p^n$ |
Здесь вероятности находятся по формуле Бернулли:
$$ P(X=k) = C_n^k \cdot p^k \cdot (1-p)^ = C_n^k \cdot p^k \cdot q^, k=0,1,2. n. $$
Числовые характеристики биномиального распределения:
Примеры многоугольников распределения для $n=5$ и различных вероятностей:
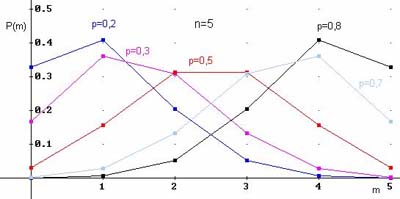
Пуассоновское распределение ДСВ
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
При условии $p\to 0$, $n \to \infty$, $np \to \lambda = const$ закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность $p$ события $A$ в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Ряд распределения по закону Пуассона имеет вид:
| $x_k$ | 0 | 1 | . | k | . |
| $p_k$ | $e^<-\lambda>$ | $\lambda e^<-\lambda>$ | . | $\frac<\lambda^k>\cdot e^<-\lambda>$ | . |
Вероятности вычисляются по формуле Пуассона:
Числовые характеристики для распределения Пуассона:
Разные многоугольники распределения при $\lambda = 1; 4; 10$.
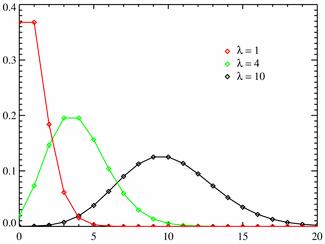
Геометрическое распределение ДСВ
Пусть происходит серия независимых испытаний, в каждом из которых событие может появится с одной и той же вероятностью $p$. Тогда случайная величина $X$ - количество испытаний до первого появления события, имеет геометрическое распределение вероятностей.
Формула для вероятностей:
$$ P(X=k) = q^k \cdot p, k=0,1,2. n. $$
Ряд распределения геометрического закона:
| $x_k$ | 0 | 1 | 2 | . | k | . |
| $p_k$ | $p$ | $q\cdot p$ | $q^2 \cdot p$ | . | $q^k \cdot p$ | . |
Гипергеометрическое распределение ДСВ
Из урны, в которой находятся $N$ шаров ($K$ белых и $N-K$ чёрных шаров), наудачу и без возвращения вынимают $n$ шаров ($n \le N$). Найти закон распределения случайной величины $X$ - равной числу белых шаров среди выбранных.
Случайная величина $X$ может принимать целые значения от $0$ до $K$ (если $n \lt K$, то до $n$). Вероятности вычисляются по формуле: $$ P(X=k)=\frac^>, \quad 0\le k \le K. $$
$$M(X)=\frac\cdot n, \quad D(X)=\frac\cdot n \cdot \frac \cdot \frac.$$
Непрерывные случайные величины
Показательное распределение НСВ
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Плотность распределения величины $X$(везде $ \lambda \gt 0)$:
Функция распределения величины $X$:
Числовые характеристики можно найти по формулам:
Плотность распределения при различных значениях $\lambda \gt 0$:
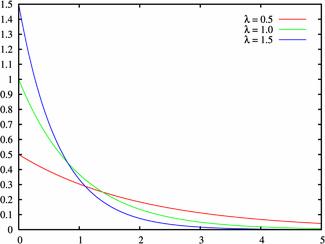
Равномерное распределение НСВ
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.
Плотность распределения на отрезке $(a;b)$:
$$ f(x)= \left\< \begin 0,\ x \le a\\ \frac ,\ a \lt x \le b, \\ 0,\ x \gt b, \\ \end \right. $$
$$ F(x)= \left\< \begin 0,\ x \le a\\ \frac ,\ a \lt x \le b, \\ 1,\ x \gt b, \\ \end \right. $$
Числовые характеристики равномерно распределенной случайной величины:
График плотности вероятностей:
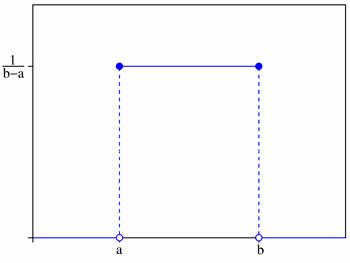
Нормальное распределение или распределение Гаусса НСВ
Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.
Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Плотность распределения нормальной случайной величины $X$ имеет вид:
При $a=0$ и $\sigma=1$ эта функция принимает вид:
Числовые характеристики для нормального распределения:
Пример графика плотности распределения для различных значений среднего и СКО:
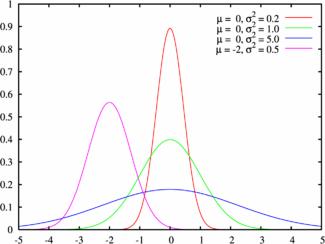
Нормальный закон распределения случайной величины с параметрами $a=0$ и $\sigma=1$ называется стандартным или нормированным, а соответствующая нормальная кривая - стандартной или нормированной.
Функция Лапласа определяется как:
Вероятность попадания нормально распределенной случайной величины $X$ в заданный интервал $(\alpha, \beta)$:
$$ P(\alpha \lt X \lt \beta) = \Phi\left( \frac \right) - \Phi\left( \frac \right). $$
Вероятность отклонения нормально распределенной случайной величины $X$ на величину $\delta$ от математического ожидания (по модулю).
Большим достоинством показательного распределения является тот факт, что оно определяется всего лишь одним параметром. Всего лишь одним, Карл! …нет, лучше, конечно, вообще отсутствие параметров, но дальше их количество будет только возрастать =)
Как-то так получилось, что во всех примерах статьи о равномерном распределении мы начинали с функции , и поэтому для разнообразия зайдём в лес с другой стороны:
Непрерывная случайная величина задана своей функцией распределения:
1) определить коэффициент ;
2) найти плотность распределения вероятностей ;
3) схематично построить графики функций и ;
4) вычислить математическое ожидание и дисперсию ;
5) определить вероятность того, что примет значение из интервала .
Одним словом, обычная задача на НСВ бессмысленная и беспощадная.
Решаем:
1) В силу непрерывности функции распределения:
– при этом и только при этом значении предложенная функция задаёт закон распределения непрерывной случайной величины:
Пока, кстати, мы не знаем, что это за закон, ведь вверху я привёл другое определение.
2) Найдём функцию плотности распределения:
надеюсь, все в ладах с производной сложной функции: .
Ну вот, теперь избушка повернулась к нам передом, а к лесу задом. Поскольку данная функция имеет вид , то случайная величина распределена показательно. Даже образцово-показательно, т.к. значение наиболее приятно.
3) Условие допускает схематическое построение графиков, но зачем занижать планку? Даже при их ручном построении не составляет никакого труда найти пару дополнительных точек и проявить маломальскую аккуратность.
Кстати, о чём идёт речь в 5-м пункте условия? В контексте рассматриваемого примера, нам нужно найти – вероятность того, что лампочка проработает более 2 тыс. часов (значения, естественно, условные). Давайте сразу и вычислим эту вероятность:
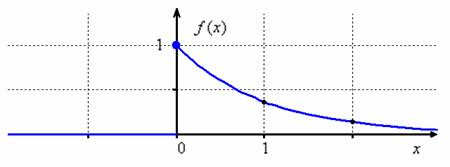
Ситуацию наглядно иллюстрирует чертёж ПЛОТНОСТИ распределения вероятностей:
Площадь между графиком и осью абсцисс равна единице (проверено в начале статьи), и значительная часть этой площади (а именно, ) сосредоточена на промежутке от 0 до 2.
И, наверное, все поняли, что несобственный интеграл – есть вероятность того, что лампочка проработает более тыс. часов, и Пункт 5 можно решить вторым способом:
4) Вычислим математическое ожидание и дисперсию.
Здесь есть короткий путь, и есть универсальный. Начнём с общей формулы математического ожидания, которая приводит нас к следующему несобственному интегралу:
Сначала удобно найти неопределенный интеграл:
, произвольную константу приплюсовывать не надо, т.к. она всё равно сократится:
Дробь по той причине, что знаменатель более высокого порядка роста, чем числитель.
Дисперсию вычислим по формуле:
И из избушки на курьих ножках появляется следующий интеграл:
Как и в случае с матожиданием, сначала проясним первообразную:
По канонам жанра тут нужно дважды интегрировать по частям, но решение облегчается тем, что после 1-го применения формулы мы сталкиваемся с только что решённым интегралом:
Таким образом, несобственный интеграл:
Здесь по той же самой причине – порядок роста.
И, наконец, дисперсия:
Пункты решения можно переставлять, т.к. они бывают расположены неудобно, а иногда и совершенно несуразно.
Показательное распределение нашло широкое применение в теории надёжности, и этой теме даже посвящены отдельные главы учебного пособия В.Е. Гмурмана. Помимо лампочек и более грустных примеров существуют и другие приложения. Так, например, в простейшем потоке событий, время ожидания каждого последующего события распределено по экспоненциальному закону. Проанализируйте работу диспетчера такси самостоятельно.
И для самостоятельного решения я предлагаю вам не только интересное, но ещё и крайне полезное Задание:
1) Дать определение показательного распределения вторым способом, с помощью функции распределения.
В начале статьи я привёл формулировку через плотность , и теперь ваша очередь – найдите функцию и запишите грамотный ответ на поставленный вопрос.
2) Вывести формулы математического ожидания и дисперсии.
Фактически тут нужно решить задачу в общем виде.
3) Записать закон распределения для и вычислить и .
Полученными формулами можно пользоваться и на практике, но с оглядкой. Будьте готовы к тому, что вас попросят привести подробные выкладки.
Дополнительных примеров с показательным распределением совсем немного. Впрочем, мы только что охватили все возможные случаи =) Вот она, мощь одного параметра.
Да, в сводном справочнике по теории вероятностей, конечно, приведены все частные формулы, но очень важно, чтобы вы умели получать их самостоятельно, исходя из общих определений. Это один из основополагающих принципов изучения математики, который красной нитью проходит через все её разделы.
Ну а сейчас пришло время зажечь новые огни и перейти к кульминационной статье под названием Нормальное распределение вероятностей.
1) Составим функцию :
– На интервале и .
– На промежутке , следовательно:
Показательным называют распределение, которое характеризуется функцией:
, где
2) Вычислим математическое ожидание:
Сначала найдём неопределённый интеграл:
Интегрируем по частям:
Дисперсию вычислим по формуле:
Сначала найдём неопределенный интеграл:
Интегрируем по частям:
Таким образом, дисперсия:
3) Запишем показательный закон для :
Вычислим математическое ожидание и дисперсию:
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
О непрерывной случайной величине (НСВ) я неоднократно упоминал в предыдущих статьях, и поэтому, если вы зашли с поисковика и/или не совсем в теме, то начните с первого урока о случайных величинах. После чего продолжаем и сразу вспоминаем разницу:
– В отличие от дискретной случайной величины, НСВ может принять любое действительное значение из некоторого промежутка ненулевой длины, что делает невозможным её представление в виде таблицы (т.к. действительных чисел несчётно много). В этой связи непрерывную случайную величину задают функциями двух типов, названия которых вы видите в заголовке.
Функция распределения непрерывной случайной величины определяется точно так же, как и функция распределения ДСВ:
Важной особенностью является тот факт, что функция распределения ЛЮБОЙ непрерывной случайной величины всегда и всюду непрерывна! Часто её можно встретить в кусочном виде, например:
и если там разрыв, то вы имеете дело с опечаткой или откровенной ошибкой!
! Но сама по себе непрерывность и ноль слева, единица справа – ещё не означают, что перед нами функция распределения.
Что касаемо масштаба, то смотрим по ситуации, чаще всего оптимальный масштаб составляет 1 ед. = 1 см (две клетки), но поскольку я строю графики не от руки, то особо не слежу за пропорциями – в данном случае по оси ординат вышло примерно в 2 раза больше, чем по оси абсцисс.
– вероятность того, что случайная величина примет значение, МЕНЬШЕЕ, чем –1;
– вероятность того, что случайная величина примет значение, МЕНЬШЕЕ, чем 4.
Ну, и очевидно, что рассматриваемая случайная величина принимает случайные, наперёд неизвестные значения из отрезка . Если вкладывать в задачу содержательный смысл, то это может быть случайная продолжительность некоего процесса (в секундах, например), или масса либо размер случайно выбранного объекта (например, крупинки песка). И тому подобное – примеров масса. Конкретные задачи непременно будут, но прежде остановимся на технической стороне вопроса.
Вероятность того, что случайная величина примет значение из некоторого промежутка рассчитывается ещё проще, чем для дискретной случайной величины. Здесь нет никакой Санта-Барбары: отрезок ли нам дан, полуинтервал или интервал , соответствующую вероятность можно вычислить по единой формуле:
Примечание: в следующем параграфе мы обоснуем это утверждение
Например:
– вероятность того, что случайная величина примет значение из отрезка . И точно такими же будут вероятности ;
– вероятность того, что случайная величина примет значение из отрезка ;
– вероятность того, что случайная величина примет значение из интервала ;
Эффективный ответ на поставленный вопрос даёт
функция ПЛОТНОСТИ распределения вероятностей
или дифференциальная функция распределения. Она представляет собой производную функции распределения: .
Примечание: для дискретной случайной величины такой функции не существует
В нашем примере:
То есть, всё очень просто – берём производную от каждого куска, и порядок.
Теперь разберём весьма любопытный факт: поскольку действительных чисел несчётно много, то вероятность того, что случайная величина примет какое-то конкретное значение стремится к нулю. И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадались:
(синяя площадь на чертеже) – вероятность того, что случайная величина примет значение из отрезка ;
(красная площадь) – вероятность того, что случайная величина примет значение из отрезка .
По той причине, что отдельно взятые значения можно не принимать во внимание, с помощью этих же интегралов рассчитываются и вероятности по интервалам / полуинтервалам, в частности:
Возможно, кто-то спросит: а зачем считать интегралы, если есть функция ?
Непрерывная случайная величина задана своей функцией распределения:
Найти значения и функцию . Проверить, что действительно является функцией плотности распределения. Вычислить вероятности . Построить графики .
Тренируемся самостоятельно! Если возникнут затруднения, то внимательно перечитайте вышеизложенный материал. Краткое решение и ответ в конце урока.
Вообще, типовые задачи на непрерывную случайную величину можно разделить на 2 большие группы: 1) когда дана функция , 2) когда дана функция .
В первом случае не составляет никаких трудностей отыскать функцию плотности распределения – почти всегда производные не то что простЫ, а примитивны (в чём мы недавно убедились). Но вот когда НСВ задана функцией , то нахождение функции распределения – есть более кропотливый процесс:
Непрерывная случайная величина задана функцией плотности распределения:
Найти значение и составить функцию распределения вероятностей. Вычислить . Построить графики .
Решение: найдём константу . Это классика. В подавляющем большинстве задач вам не предложат готовую функцию плотности. Используем свойство . В данном случае:
На практике нулевые интегралы можно опускать, а константу сразу выносить за знак интеграла:
Пользуясь чётностью подынтегральной функции, вычислим:
и подставим результат в уравнение:
, откуда выразим
Таким образом, функция плотности распределения:
Выполним проверку, а именно, вычислим тот же самый интеграл, но уже с известной константой. Для разнообразия я не буду пользоваться чётностью:
, что и требовалось проверить.
Обратите внимание, что только при – и только при этом значении, предложенная в условии функция является функцией плотности распределения. Ну и тут не лишним будет проконтролировать, что на интервале , т.е. условие неотрицательности выполнено. Доверяй условию, да проверяй ;) Не раз и не два мне встречались функции, которые в принципе не могли быть плотностью, что говорило об опечатках или о невнимательности авторов задач.
Теперь начинается самое интересное. Функция распределения вероятностей – есть интеграл:
Так как наша состоит из трёх кусков, то решение разобьётся на 3 шага:
1) На промежутке , поэтому:
2) На интервале , и мы прицепляем следующий вагончик:
3) И, наконец, на , и детский паровозик отправляется в путь:
! А вот в этом задании нулевые интегралы пропускать НЕ НАДО. Чтобы показать своё понимание функции распределения ;) К тому же, они могут оказаться вовсе не нулевыми, и тогда придётся иметь дело с интегралами несобственными. Соответствующие примеры я обязательно разберу ниже.
Записываем наши достижения под единую скобку:
– вероятность того, что случайная величина примет значение из промежутка
Но ценители интегрального исчисления, конечно же, не откажут себе в удовольствии:
, что, кстати, не труднее. И проверочка заодно получилась.
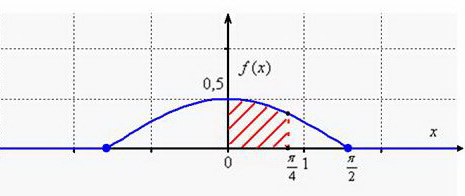
Выполним чертежи. График представляет собой косинусоиду, сжатую вдоль ординат в 2 раза:
Тот редкий случай, когда функция плотности непрерывна.
Чертежи желательно расположить так, чтобы оси ординат лежали ровненько одна под другой. Это будет хорошим тоном.
И я так чувствую, вам уже не терпится проверить свои силы. Как водится, пример попроще:
Задана плотность распределения вероятностей непрерывной случайной величины :
Требуется:
1) определить коэффициент ;
2) найти функцию распределения ;
3) построить графики ;
4) найти вероятность того, что примет значение из промежутка
и задачка поинтереснее:
Непрерывная случайная величина задана плотностью распределения вероятностей:
Найти значение и построить график плотности распределения. Найти функцию распределения вероятностей и построить её график. Вычислить вероятность .
Дерзайте! Свериться с решением можно внизу страницы.
И в заключение 1-й части урока обещанные случаи с несобственными интегралами:
Непрерывная случайная величина задана своей плотностью распределения:
Найти коэффициент и функцию распределения . Построить графики.
Решение: по свойству функции плотности распределения:
В данной задаче состоит из 2 частей, поэтому:
Таким образом, наше уравнение превратилось в готовый результат:
и функция плотности:
Функция , как нетрудно понять, отыскивается в 2 шага:
1) На промежутке , следовательно:
– вот такая вот у нас замечательная экспонента. Как птица Феникс.
2) На интервале и:
, что и должно получиться.
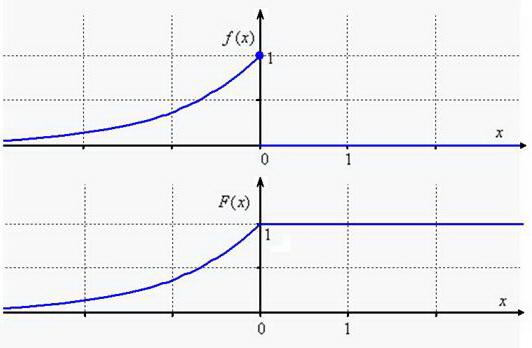
Для построения графиков найдём пару опорных точек: и аккуратно прочертим кусочки экспонент с причитающимися дополнениями:
Заметьте, что теоретически случайная величина может принять сколь угодно большое по модулю отрицательное значение, и ось абсцисс является горизонтальной асимптотой для обоих графиков при .
Ещё более интересное задание для самостоятельного изучения:
Проверить, что является функцией плотности распределения вероятностей непрерывной случайной величины. Найти и выполнить чертежи.
Решения и ответы:
Пример 1. Решение: в силу непрерывности функции распределения:
Таким образом:
Найдём функцию плотности распределения:
Покажем, что действительно является функцией плотности:
1) Для любого значения , в частности, на среднем промежутке:
Внимание! Без 1-го пункта обойтись нельзя!
2)
Таким образом, найденная функция действительно является функцией плотности распределения.
Требуемые вероятности выгоднее вычислить с помощью функции распределения:
– вероятность того, что случайная величина примет значение из полуинтервала ;
– вероятность того, что случайная величина примет значение, больше, чем .
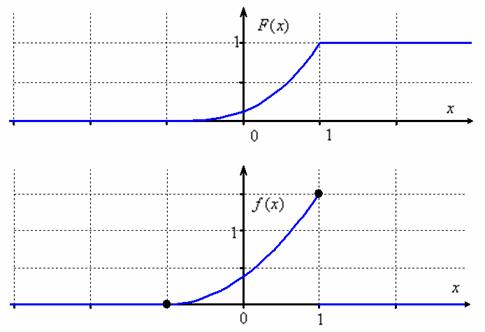
Построим графики :
Пример 3. Решение:
1) По свойству функции плотности распределения:
В данной задаче:
Таким образом, искомая плотность:
2) Функцию распределения найдём с помощью формулы :
– если то и ;
– если то и ;
– если то и:
.
Таким образом:
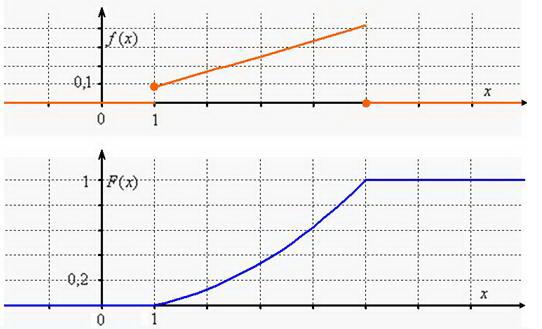
3) Выполним чертежи:
4) Найдём вероятность того, что случайная величина примет значение из промежутка :
Пример 4. Решение: функция плотности распределения вероятности обладает свойством . В данном случае:
Таким образом, функция плотности распределения:
Выполним чертеж:
Составим функцию распределения вероятностей :
1) Если , то и
2) Если , то и
3) Если , то и:
4) Если , то и:
Таким образом:
,
Выполним чертеж:
Вычислим – вероятность того, что случайная величина примет значение из интервала .
Пример 6. Решение: проверим, что функция является функцией плотности:
1) Поскольку экспоненциальная функция положительна, то для любого , значит, свойство неотрицательности функции плотности выполнено.
2) Проверим выполнение свойства . Сначала удобно найти неопределённый интеграл:
.
Используем чётность подынтегральной функции:
Вывод: является функцией плотности распределения вероятностей непрерывной случайной величины, что и требовалось проверить.
Найдём функцию распределения:
– для всех .
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ - распределенных по показательному (или экспоненциальному) закону.
Плотность распределения величины $X$ с экспоненциальным законом распределения задается формулой:
Функция распределения величины $X$:
Здесь $\lambda$ - единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: $M(X)=1/\lambda$, $D(X)=1/\lambda^2$.
Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр $\lambda$ описываетс среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.
В этом разделе мы приведем разные примеры задач с полным решением, где используются показательно распределенные случайные величины.
Примеры решений
Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 часов прибор не выйдет из строя.
Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?
Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $\lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.
Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^$ при $t\ge 0$ и $f(t)=0$ при $t\lt 0$.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.
Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^$ при $x \gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.
Задача 8. Непрерывная случайная величина $\xi$ распределена по показательному закону с параметром $\lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $\xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $\xi$ и вероятность того, что $\xi$ принимает значения, меньшие своего математического ожидания.
Задача 9. Случайная величина $\xi$ распределена по показательному закону с параметром 2. Найти $M_<\xi>$, $D_<\xi>$ вероятность попадания $\xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $\xi$.
Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(\lambda)$. Найдите вероятность события $|Х - МХ | \lt 3\sigma$ ("правило $3\sigma$" для показательного распределения).
Без преувеличения его можно назвать философским законом. Наблюдая за различными объектами и процессами окружающего мира, мы часто сталкиваемся с тем, что чего-то бывает мало, и что бывает норма:
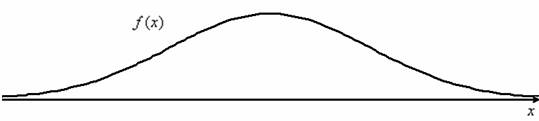
Перед вами принципиальный вид функции плотности нормального распределения вероятностей, и я приветствую вас на этом интереснейшем уроке.
Непрерывная случайная величина , распределённая по нормальному закону, имеет функцию плотности (не пугаемся) и однозначно определяется параметрами и .

Данная функция получила фамилию некоронованного короля математики, и я не могу удержаться, чтобы не запостить:
Одну из таких купюр мне довелось лично держать в руках, и ещё будучи школьником я внимательно изучил функцию Гаусса. Педантичные немцы отобразили все её особенности (на картинке видно плохо), и мы с толком, с расстановкой приступаем к их немцев изучению.
Начнём с того, что для функции выполнены свойства плотности вероятностей , а именно (почему?) и , откуда следует, что нормально распределённая случайная величина достоверно примет одно из действительных значений. Теоретически – какое угодно, практически – узнаем позже.
Любопытно отметить, что сам по себе неопределённый интеграл является неберущимся, однако указанный выше несобственный интеграл сходится и равен . Вычисления для простейшего случая можно найти здесь, все же остальные варианты сводятся к нему с помощью линейной замены .
Следующие замечательные факты я тоже приведу без доказательства:
Эти значения выводятся с помощью общих формул математического ожидания и дисперсии, и желающие / нуждающиеся могут ознакомиться с подробными выкладками в учебной литературе, и совсем здОрово, если вам удастся провести их самостоятельно.
Нормально распределённая случайная величина задана параметрами . Записать её функцию плотности и построить график.
Несмотря на кажущуюся простоту задания, в нём существует немало тонкостей.
Решение начнём шаблонной фразой: функция плотности нормально распределённой случайной величины имеет вид . В данном случае и:
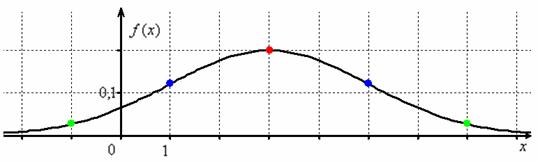
Сначала полная картина, затем комментарии:
Строим декартову систему координат. При выполнении чертежа от руки во многих случаях оптимален следующий масштаб:
по оси абсцисс: 2 тетрадные клетки = 1 ед.;
по оси ординат: 2 тетрадные клетки = 0,1 ед., при этом саму ось следует расположить из тех соображений, что в точке функция достигает максимума, и вертикальная прямая (на чертеже отсутствует) является линией симметрии графика.
И логично, что в первую очередь удобно найти максимум функции. В данном примере он находится в точке :
Отмечаем вершину графика (красная точка).
Далее вычислим значения функции при , а точнее только одно из них – в силу симметрии графика они равны:
Отмечаем синим цветом.
Внимание! – это точки перегиба нормальной кривой. На интервале график является выпуклым, а на крайних интервалах – вогнутым.
Далее отклоняемся от центра ещё на одно стандартное отклонение и рассчитываем высоту:
Отмечаем точки на чертеже (зелёный цвет) и видим, что этого вполне достаточно.
При электронном оформлении решения график легко построить в Экселе, и неожиданно для самого себя я даже записал короткий видеоролик на эту тему. Но сначала поговорим о том, как меняется форма нормальной кривой в зависимости от значений и .
Ну а теперь смотрим кино:
Почти все значения не поддаются точному расчету, но как мы только что видели, с современными вычислительными мощностями с этим нет никаких трудностей. Так, для функции стандартного распределения соответствующая экселевская функция вообще содержит один аргумент:
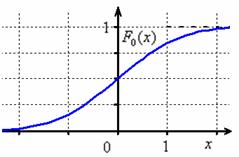
Раз, два – и готово:
На чертеже хорошо видно выполнение всех свойств функции распределения, и из технических нюансов здесь следует обратить внимание на горизонтальные асимптоты и точку перегиба .
! Вспоминаем также, что
Примечание: функцию легко получить из общего случая с помощью линейной замены . Тогда и:
и из проведённой замены как раз следует формула перехода от значений произвольного распределения – к соответствующим значениям стандартного распределения.
Зачем это нужно? Дело в том, что значения скрупулезно подсчитаны нашими предками и сведены в специальную таблицу, которая есть во многих книгах по терверу. Но ещё чаще встречается таблица значений , с которой мы уже имели дело в интегральной теореме Лапласа:
, где – функция Лапласа.
Из пункта ведётся стрельба из орудия вдоль прямой . Предполагается, что дальность полёта распределена нормально с математическим ожиданием 1000 м и средним квадратическим отклонением 5 м. Определить (в процентах) сколько снарядов упадёт с перелётом от 5 до 70м.
Решение: в задаче рассматривается нормально распределённая случайная величина – дальность полёта снаряда, и по условию .
Так как речь идёт о перелёте за цель, то . Вычислим вероятность – того, что снаряд упадёт в пределах этой дистанции.
Если в нашем распоряжении есть таблица значений функции , то используем формулу :
Если же в нашем распоряжении есть таблица значений функции Лапласа , то решаем через неё:
Дробные значения традиционно округляем до 4 знаков после запятой, как это сделано в типовой таблице. И для контроля есть Пункт 5 макета.
Напоминаю, что , и во избежание путаницы всегда контролируйте, таблица КАКОЙ функции перед вашими глазами.
Ответ требуется дать в процентах, поэтому рассчитанную вероятность нужно умножить на 100 и снабдить результат содержательным комментарием:
– с перелётом от 5 до 70 м упадёт примерно 15,87% снарядов
Диаметр подшипников, изготовленных на заводе, представляет собой случайную величину, распределенную нормально с математическим ожиданием 1,5 см и средним квадратическим отклонением 0,04 см. Найти вероятность того, что размер наугад взятого подшипника колеблется от 1,4 до 1,6 см.
В образце решения и далее я буду использовать функцию Лапласа, как самый распространённый вариант. Кстати, обратите внимание, что согласно формулировке, здесь можно включить концы интервала в рассмотрение. Впрочем, это не критично.
И уже в этом примере нам встретился особый случай – когда интервал симметричен относительно математического ожидания. В такой ситуации его можно записать в виде и, пользуясь нечётностью функции Лапласа, упростить рабочую формулу:
– вероятность того, что значение случайной величины отклонится от математического ожидания менее чем на .
Хорошо то решение, которое умещается в одну строчку:)
– вероятность того, что диаметр наугад взятого подшипника отличается от 1,5 см не более чем на 0,1 см.
Результат этой задачи получился близким к единице, но хотелось бы ещё бОльшей надежности – а именно, узнать границы, в которых находится диаметр почти всех подшипников. Существует ли какой-нибудь критерий на этот счёт? Существует! На поставленный вопрос отвечает так называемое
Его суть состоит в том, что практически достоверным является тот факт, что нормально распределённая случайная величина примет значение из промежутка .
И в самом деле, вероятность отклонения от матожидания менее чем на составляет:
или 99,73%
Продолжаем решать суровые советские задачи:
Случайная величина ошибки взвешивания распределена по нормальному закону с нулевым математическим ожиданием и стандартным отклонением 3 грамма. Найти вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей по модулю 5 грамм.
Решение очень простое. По условию, и сразу заметим, что при очередном взвешивании (чего-то или кого-то) мы почти 100% получим результат с точностью до 9 грамм. Но в задаче фигурирует более узкое отклонение и по формуле :
– вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей 5 грамм.
Ответ:
…срочно разрабатываю курс по подготовке продавцов =)
Самостоятельно решаем обратную задачу:
Диаметр валика – случайная нормально распределенная случайная величина, среднее квадратическое отклонение ее равно мм. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью попадет длина диаметра валика.
Пункт 5* расчётного макета в помощь. Обратите внимание, что здесь не известно математическое ожидание, но это нисколько не мешает решить поставленную задачу.
И экзаменационное задание, которое я настоятельно рекомендую для закрепления материала:
Нормально распределенная случайная величина задана своими параметрами (математическое ожидание) и (среднее квадратическое отклонение). Требуется:
Такие задачи предлагаются повсеместно, и за годы практики мне их довелось решить сотни и сотни штук. Обязательно попрактикуйтесь в ручном построении чертежа и использовании бумажных таблиц ;)
Ну а я разберу пример повышенной сложности:
Плотность распределения вероятностей случайной величины имеет вид . Найти , математическое ожидание , дисперсию , функцию распределения , построить графики плотности и функции распределения, найти .
Так как функция определена при любом действительном значении , и её можно привести к виду , то случайная величина распределена по нормальному закону.
Приводим. Для этого выделяем полный квадрат и организуем трёхэтажную дробь:
Обязательно выполняем проверку, возвращая показатель в исходный вид:
, что мы и хотели увидеть.
Теперь найдём значение параметра . Поскольку множитель нормального распределения имеет вид и , то:
, откуда выражаем и подставляем в нашу функцию:
, после чего ещё раз пробежимся по записи глазами и убедимся, что полученная функция имеет вид .
Построим график плотности:
и график функции распределения :
Если под рукой нет Экселя и даже обычного калькулятора, то последний график легко строится вручную! В точке функция распределения принимает значение и здесь находится перегиб графика (малиновая точка) Кроме того, для более или менее приличного чертежа желательно найти ещё хотя бы пару точек. Берём традиционное значение и стандартизируем его по формуле . Далее с помощью таблицы значений функции Лапласа находим: – жёлтая точка на чертеже. С симметричной оранжевой точкой никаких проблем: и:
.
После чего аккуратно проводим интегральную кривую, не забывая о перегибе и двух горизонтальных асимптотах.
Да, и ещё нужно вычислить:
– вероятность того, что случайная величина примет значение из данного отрезка.
Ответ:
Но этим, конечно, всё дело не ограничивается! Дополнительные примеры, причём довольно творческие, можно найти в тематической pdf-книжке.
И в заключение урока обещанный секрет:
понятие о центральной предельной теореме
которую также называют теоремой Ляпунова. Её суть состоит в том, что если случайная величина является суммой очень большого числа взаимно независимых случайных величин , влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.
В окружающем мире условие теоремы Ляпунова выполняется очень часто, и поэтому нормальное распределение (близкое к нему) и встречается буквально на каждом шагу.
Так, например, молекул воздуха очень и очень много, и каждая из них своим движением оказывает ничтожно малое влияние на всю совокупность. Поэтому скорость молекул воздуха распределена нормально.
Большая популяция некоторых особей. Каждая из них (или подавляющее большинство) оказывает несущественное влияние на жизнь всей популяции, следовательно, длина их лапок тоже распределена по нормальному закону.
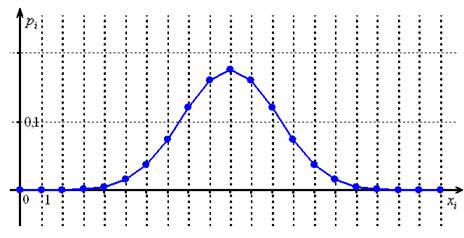
Уже при и в многоугольнике биномиального распределения хорошо просматривается нормальная кривая:
И чем больше , тем ближе будет сходство. Вероятность может быть и другой, но не слишком малой.
Именно этот факт мы и использовали в теоремах Лапласа – когда приближали биномиальные вероятности соответствующими значениями функций нормального распределения.
Вот такие вот пироги.
До скорых встреч!
Решения и ответы:
Пример 3. Решение: т.к. случайная величина (диаметр подшипника) распределена нормально, то используем формулу , где – функция Лапласа. В данном случае:
– вероятность того, что диаметр наугад взятого подшипника будет находиться в пределах от 1,4 до 1,6 см.
Пример 5. Решение: используем формулу: .
В данной задаче , таким образом:
откуда находим:
Длина искомого интервала составляет
Ответ: 20 мм
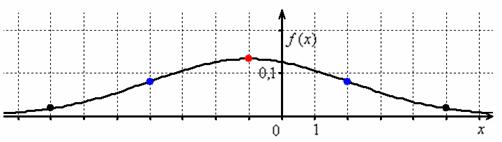
Пример 6. Решение: функция плотности нормально распределённой случайной величины имеет вид , где – математическое ожидание, – стандартное отклонение. В данном случае , следовательно:
Выполним чертёж:
! Примечание: несмотря на то, что условие допускает схематическое построение графика, на чертеже обязательно отображаем все его принципиальные особенности, в частности, на забываем о перегибах в точках .
б) Используем формулу , где – функция Лапласа.
В данной задаче :
– вероятность того, что случайная величина примет значение из данного интервала.
в) Используем формулу для :
– вероятность того, что значение случайной величины отклонится от её математического ожидания не более чем на 2.
Ответ: а) , б) , в) , г)
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Читайте также:

