Лямбда характеристика и средняя наработка на отказ

Обновлено: 29.01.2025

В современном постоянно движущемся мире сбои в работе и технические инциденты становятся как никогда важными. Ошибки и простои ведут к реальным последствиям. Пропущенные сроки. Задержки оплаты. Задержки работы по проектам.

Вот почему для компаний важно количественно оценивать и отслеживать показатели безотказной работы, времени простоя и того, как быстро и эффективно команды решают проблемы.

Некоторые из наиболее часто отслеживаемых в отрасли метрик: MTBF (средняя наработка на отказ), MTTR (среднее время восстановления, исправления, реагирования или устранения), MTTF (средняя наработка до отказа) и MTTA (среднее время подтверждения) — эти метрики предназначены для того, чтобы помочь техническим командам понять, как часто происходят инциденты и как быстро команда справляется с ними.

Многие эксперты спорят о действительной пользе этих метрик, если использовать их в отрыве от остальных показателей, потому что они не дают ответа на сложные вопросы о том, как устраняются инциденты, что работает, а что нет, и как, когда и почему проблемы обостряются или ослабляются.

С другой стороны, MTTR, MTBF и MTTF могут быть хорошей основой или эталоном, с которых стоит начинать обсуждение более глубоких и важных вопросов.

Как профессионалы реагируют на крупные инциденты

Получите наше бесплатное руководство по управлению инцидентами. Изучите все инструменты и методы, которые Atlassian использует для управления крупными инцидентами.

Оговорка об MTTR

Поэтому если вашей команде нужно отслеживать MTTR, рекомендуется уточнить, какой именно MTTR имеется в виду и как его определить. Прежде чем вы начнете отслеживать успехи и неудачи, у вашей команды должно быть общее понимание того, что именно вы отслеживаете.

MTBF: средняя наработка на отказ

Что такое средняя наработка на отказ?

MTBF (средняя наработка на отказ) — это среднее время между исправляемыми сбоями технологического продукта. Эта метрика используется для отслеживания как доступности, так и надежности продукта. Чем больше времени проходит между отказами, тем надежнее система.

Цель для большинства компаний — сохранить наработку на отказ как можно выше, достигнув сотни тысяч (или даже миллионов) часов между инцидентами.

Как рассчитать среднюю наработку на отказ

MTBF рассчитывается с использованием среднего арифметического. По сути, вы должны взять данные за период, на который вы хотите рассчитать MTBF (можно за шесть месяцев, год, за пять лет), и поделить общее время работы за этот период на количество сбоев.

Итак, предположим, что мы оцениваем 24-часовой период и за этот период мы потеряли два часа из-за двух отдельных инцидентов. Наше общее время безотказной работы составляет 22 часа. Разделим на два и получаем 11 часов. Итак, наша наработка на отказ составляет 11 часов.

Поскольку эта метрика используется для отслеживания надежности, наработка на отказ не учитывает ожидаемое время простоя во время планового технического обслуживания. Вместо этого она фокусируется на неожиданных простоях и проблемах.

Происхождение понятия средней наработки на отказ

MTBF берет свое начало в авиационной отрасли, где системные сбои означают особенно серьезные последствия не только с точки зрения стоимости, но и человеческой жизни. С тех пор эта аббревиатура пробралась в различные технические и механические отрасли промышленности и особенно часто используется в производстве.

Как и когда использовать среднюю наработку на отказ

Время наработки на отказ полезно для покупателей, которые хотят быть уверены, что получают самый надежный продукт, полетят на самом надежном самолете или выберут самое безопасное производственное оборудование для своего завода.

Для внутренних команд эта метрика помогает выявлять проблемы и отслеживать успехи и неудачи. Она также может помочь компаниям разработать подробные рекомендации для клиентов, чтобы они знали, когда они должны заменить деталь, обновить систему или принести продукт на техническое обслуживание.

MTBF — это метрика для сбоев в восстанавливаемых системах. Для сбоев, требующих замены системы, обычно используют термин MTTF (средняя наработка до отказа).

Например, представьте двигатель автомобиля. При расчете времени между внеплановыми техническими обслуживаниями двигателя следует использовать MTBF (среднюю наработку на отказ). При расчете времени до полной замены двигателя вы должны использовать MTTF (среднюю наработку до отказа).

MTTR: среднее время исправления

Что такое среднее время исправления?

MTTR (среднее время ремонта) — это среднее время, необходимое для ремонта системы (обычно технического или механического). Оно включает в себя как время ремонта, так и любое время тестирования. В этой метрике учитывается все время до тех пор, пока система не будет снова полностью работоспособна.

Как рассчитать среднее время исправления

Вы можете рассчитать MTTR, суммируя общее время, затраченное на ремонт в течение любого заданного периода, а затем разделив это время на количество ремонтов.

Итак, предположим, мы считаем эту метрику для ремонта в течение недели. За это время было 10 простоев, и системы активно ремонтировались в течение четырех часов. Четыре часа — это 240 минут. 240 делим на 10 и получаем 24. Что означает, что среднее время ремонта в этом случае будет составлять 24 минуты.

Ограничения среднего времени исправления

Среднее время ремонта не всегда совпадает с тем же временем, что и время сбоя работы системы. В некоторых случаях ремонт начинается в течение нескольких минут после сбоя продукта или сбоя системы. В других случаях между собственно инцидентом, обнаружением инцидента и началом ремонта бывает некоторая задержка.

Эта метрика наиболее полезна при отслеживании того, как быстро обслуживающий персонал может устранить проблему. Она не предназначена для выявления проблем с системными оповещениями или задержками перед восстановлением, которые также являются важными факторами при оценке успехов и сбоев программы управления инцидентами.

Как и когда использовать среднее время исправления

MTTR — это метрика, которую используют команды поддержки и технического обслуживания для обеспечения восстановительных работ на нужном уровне. Цель состоит в том, чтобы этот показатель был как можно ниже за счет повышения эффективности процессов восстановления и продуктивности команд.

MTTR: среднее время восстановления

Что такое среднее время восстановления?

MTTR (среднее время восстановления или среднее время стабилизации) — это среднее время восстановления после сбоя работы продукта или системы. Оно включает в себя полное время простоя с момента выхода из строя системы или продукта до момента, когда они снова становятся полностью работоспособными.

Это основной показатель DevOps, который, по мнению программы DevOps Research and Assessment (DORA), можно использовать для оценки стабильности команды DevOps.

Как рассчитать среднее время восстановления

Среднее время восстановления рассчитывается путем суммирования всего времени простоя в работе за определенный период и деления его на количество инцидентов. Итак, предположим, что наши системы были отключены на 30 минут в течение двух отдельных инцидентов за 24-часовой период. 30 делим на два, получаем 15, так что наш MTTR составляет 15 минут.

Ограничения среднего времени восстановления

MTTR используется для измерения скорости полного процесса восстановления. Достаточно ли она высокая? А по сравнению с вашими конкурентами?

Эта общая метрика помогает определить, есть ли у вас проблемы. Однако если вы хотите диагностировать, в какой именно части вашего процесса есть проблема (проблема в вашей системе оповещений? команда слишком много времени работает над исправлением? кто-то слишком долго отвечает на запрос на исправление?), то вам понадобится больше данных. Потому что между сбоем и восстановлением может произойти много чего.

Проблема может быть связана с вашей системой оповещения. Существует ли задержка между сбоем и отправкой оповещения? Достаточно ли быстро оповещения доходят до нужного человека?

Проблема может быть в диагностике. Можете ли вы быстро выяснить, в чем проблема? Существуют ли процессы, которые можно было бы улучшить?

Или проблема может быть с самим процессом исправления. Достаточно ли эффективны ваши команды технического обслуживания? Если они тратят все свое время на исправление, то что именно их тормозит?

Вам нужно будет копнуть глубже, чем MTTR, чтобы ответить на эти вопросы, но среднее время восстановления может стать отправной точкой для диагностики того, существует ли проблема в процессе восстановления и требует ли она более глубокого анализа.

Как и когда использовать среднее время восстановления

MTTR является хорошей метрикой для оценки скорости общего процесса восстановления.

MTTR: среднее время разрешения

Что такое среднее время разрешения?

MTTR (среднее время разрешения) — это среднее время, необходимое для полного устранения сбоя. Оно включает в себя не только время, затраченное на обнаружение сбоя, диагностику проблемы и ее устранение, но и время, затраченное на предотвращение повторения проблемы.

Эта метрика расширяет ответственность команды, обрабатывающей исправление: она задает ожидания в плане повышения ее продуктивности в долгосрочной перспективе. В этом и заключается разница между простым тушением пожара и тушением пожара с последующей установкой противопожарной системы.

Существует сильная связь между этим MTTR и удовлетворенностью клиентов, так что этой метрике нужно уделить особое внимание.

Как рассчитать среднее время разрешения

Чтобы рассчитать этот MTTR, рассчитайте полное время разрешения в течение периода, который вы хотите отслеживать, и разделите на количество инцидентов.

Таким образом, если ваши системы были отключены в общей сложности 2 часа за 24-часовой период из-за одного инцидента и команды потратили еще 2 часа на исправление, чтобы гарантировать, что сбой системы не повторится, в сумме получается 4 часа, потраченных на решение проблемы. Это означает, что ваш MTTR составляет 4 часа.

Заметка об отслеживании среднего времени разрешения

Имейте в виду, что MTTR чаще всего рассчитывается с использованием рабочих часов (поэтому если вы восстановите работу в конце рабочего дня и потратите время на исправление основной проблемы первым делом на следующее утро, ваш MTTR не будет включать 16 часов, в течение которых вы не работали). Если у вас есть команды в разных часовых поясах и вы работаете круглосуточно или если у вас есть дежурные сотрудники, работающие во внеурочное время, важно определить, как вы будете отслеживать время для этой метрики.

Как и когда использовать среднее время разрешения

MTTR обычно используется, когда речь идет о незапланированных инцидентах, а не о запросах на обслуживание (которые обычно планируются).

MTTR: среднее время реагирования

Что такое среднее время реагирования?

MTTR (среднее время реагирования) — это среднее время, необходимое для восстановления после сбоя продукта или системы с момента первого оповещения об этом сбое. Оно не включает время задержки в вашей системе оповещения.

Как рассчитать среднее время реагирования

Чтобы рассчитать этот MTTR, рассчитайте полное время отклика с момента получения оповещения до того, когда продукт или услуга снова полностью функционируют. Затем разделите его на количество инцидентов.

Например: если у вас было 4 инцидента за 40-часовую рабочую неделю и вы потратили на них 1 час (от оповещения до исправления), то MTTR за эту неделю будет составлять 15 минут.

Как и когда использовать среднее время реагирования

MTTR часто используется в кибербезопасности при измерении успеха команды в нейтрализации атак на систему.

MTTA: среднее время подтверждения

Что такое среднее время подтверждения?

MTTA (среднее время подтверждения) — это среднее время, которое проходит с момента отправки оповещения до начала работы над исправлением. Эта метрика полезна для измерения скорости реагирования вашей команды и эффективности вашей системы оповещения.

Как рассчитать среднее время подтверждения

Чтобы рассчитать MTTA, посчитайте время между отправкой оповещения и подтверждением его получения, а затем разделите на количество инцидентов.

Например: если у вас было 10 инцидентов и в общей сложности прошло 40 минут между отправкой оповещения и подтверждением его получения для всех 10, вы поделите 40 на 10 и получите в среднем 4 минуты.

Как и когда использовать среднее время подтверждения

MTTF: средняя наработка до отказа

Что такое средняя наработка до отказа?

MTTF (средняя наработка до отказа) — среднее время между неремонтируемыми отказами технологического продукта. Например, если автомобильные двигатели марки X исправно работают в среднем 500 000 часов, до того как они полностью выйдут из строя и будут подлежать замене, MTTF двигателей будет составлять 500 000.

Эта метрика помогает понять, как долго система будет исправно работать, и определить, превосходит ли новая версия системы старую. Метрика позволяет предоставить клиентам информацию об ожидаемом сроке исправной работы и о том, когда следует запланировать проверку системы.

Как рассчитать среднюю наработку до отказа

Средняя наработка до отказа — это среднее арифметическое, которое определяется как сумма общего времени работы оцениваемых продуктов, деленная на общее количество устройств.

Например: предположим, вы рассчитываете MTTF лампочек. Как долго лампочки бренда Y в среднем работают, прежде чем они перегорают? Далее предположим, что для расчета у вас есть четыре лампочки (если вам нужны статистически значимые данные, вам понадобится гораздо больше, но, чтобы не перегружать вас расчетами, давайте возьмем всего четыре).

Лампочка А горит 20 часов. Лампочка B — 18. Лампочка C —21. И лампочка D —21 час. Это в общей сложности 80 часов горения лампочки. Делим на четыре и получаем MTTF в 20 часов.

Проблема, связанная со средней наработкой до отказа

Для таких случаев, как лампочки, смысл MTTF совершенно ясен. Мы можем включить лампочки и ждать до тех пор, пока не перегорит последняя, а затем использовать полученную информацию, чтобы сделать выводы о времени работы наших лампочек.

Но что происходит, когда мы измеряем что-то, что не перегорает так быстро? Что-то, что должно бесперебойно работать в течение долгих лет? Хотя MTTF часто используется и для этих случаев, эта метрика — не лучший выбор. Потому что мы не держим продукт включенным до тех пор, пока он не выйдет из строя; в основном мы запускаем продукт на определенный период времени и измеряем количество выходов из строя.

Например: предположим, что мы пытаемся получить статистику MTTF на планшетах бренда Z. Планшеты по-хорошему рассчитаны на долгие годы, но у бренда Z есть всего шесть месяцев для сбора данных. Поэтому тестируют 100 планшетов в течение шести месяцев. Допустим, один планшет ломается ровно на шестимесячной отметке.

Итак, мы умножаем общее время работы (полгода, умноженное на 100 планшетов) и получаем 600 месяцев. Только один планшет вышел из строя, так что мы разделим значение на один, и наш MTTR будет составлять 600 месяцев, то есть 50 лет.

Прослужат ли планшеты Brand Z в среднем 50 лет каждый? Маловероятно. И поэтому эта метрика не подходит в таких случаях.

Как и когда использовать среднюю наработку до отказа

MTTF хорошо работает, когда вы пытаетесь оценить средний срок службы продуктов и систем с коротким сроком службы (например, лампочек). Показатель предназначен только для случаев, когда оценивается полное прекращение работы продукта. При расчете времени между инцидентами, требующими восстановления, предпочтительной аббревиатурой является MTBF (средняя наработка на отказ).

MTBF, MTTR, MTTF и MTTA

Итак, какую метрику лучше использовать, когда дело доходит до отслеживания и улучшения управления инцидентами?

Хотя они иногда используются взаимозаменяемо, каждая метрика позволяет рассмотреть ситуацию с разных сторон. При совместном использовании они могут показать более полную картину и дать вам понять, насколько успешна ваша команда в управлении инцидентами и что она может улучшить.

Среднее время восстановления показывает, как быстро у вас получается возобновить работу ваших систем.

Рассчитайте среднее время реагирования, и вы получите представление о том, сколько времени восстановления тратится на работу вашей команды и сколько — на получение оповещения.

Потом рассчитайте среднее время исправления, и вы поймете, сколько времени команда тратит на исправление, а сколько на диагностику.

Теперь рассчитайте среднее время разрешения, и вы начнете понимать весь процесс исправления и решения проблем, выходящий за рамки самого простоя, который они вызывают.

Посчитайте среднюю наработку на отказ, и картина станет еще шире: вы увидите, насколько успешна ваша команда в предотвращении или сокращении будущих проблем.

А затем добавьте среднюю наработку до отказа, чтобы понять полный жизненный цикл продукта или системы.

Jira Service Management предлагает возможности создания отчетов, чтобы ваша команда могла отслеживать KPI, а также контролировать и оптимизировать управление инцидентами.

Для оценки безотказности изделий используют следующие показатели:

P(t) – вероятность безотказной работы за время t;

Q(t) – вероятность отказа;

T_ср – средняя наработка до первого отказа (или среднее время безотказной работы);

T_о – средняя наработка на отказ;

T – средняя наработка между отказами;

λ(t) – интенсивность отказов;

λ₁(t) – параметр потока отказов – для восстанавливаемых изделий;

ω(t) – средняя частота отказов.

Кроме вышеперечисленных, могут использоваться и другие критерии, оценивающие то или иной фактор в зависимости от особых условий работы изделия.

Показатели безотказности могут вводиться как по отношению ко всем возможным отказам изделия, так и по отношению к какому-либо одному типу отказа.

Очевидно, что изделие работает безотказно, если оно при этом сохранят свои рабочие параметры в установленных пределах в течение рассматриваемого промежутка времени t.

Вероятность безотказной работы отдельного изделия оценивается так:

где T – время от начала работы до отказа;

t – время, для которого определяется вероятность безотказной работы.

Величина Т может быть больше, меньше или равна t. Следовательно 0 ≤ P(t) ≤ 1.

Вероятность безотказной работы – это статистический и относительный показатель сохранения работоспособности однотипных изделий серийного производства, выражающий вероятность того, что в предела заданной наработки отказ изделий не наступает. Для установления значения вероятности безотказной работы серийных изделий используют формулу для среднестатистического значения:

где N – число наблюдаемых изделий (или элементов);

N₀ – число отказавших изделий за время t;

N_p – число работоспособных изделий к концу времени t испытаний или эксплуатации.

Вероятность безотказной работы является одной из наиболее значимых характеристик надёжности изделия, так как она охватывает все факторы влияющие на надёжность. Для вычисления вероятности безотказной работы используются данные, накапливаемые путём наблюдений за работой при эксплуатации или специальных испытаниях. Чем больше изделий подвергается наблюдениям или испытаниям на надёжность, тем точнее определяется вероятность безотказной работы других однотипных изделий.

Так как безотказная работа и отказ – взаимно противоположные события, то оценку вероятности отказа (Q(t)) определяют по формуле:

Распределение отказов во времени характеризуется функцией плотности распределения (t) наработки до отказа. Статистическая оценка плотности распределения имеет вид:

где ∆N(t) – приращение числа отказавших изделий за время ∆t.

В вероятностном смысле плотность распределения наработки до отказа

Вероятности отказов и безотказной работы в функции плотности распределения наработки на отказ выражаются зависимостями:

Рис.7.2.Типичное изменение вероятности безотказной работы изделия во времени.

Относительная безотказность P(t), определенная на основе экспериментальных данных, служит отправной характеристикой при проектировании новой аналогичной техники с повышенной надежностью.

При проектировании методом расчета оценивают возможное значение P(t) будущего изделия. Повышается P(t) от использования более надежных деталей и элементов (блоков, частей), от повышения надежности методов работы техники, от оптимизации структурных схем изделий, а также от использования более эффективных технологий изготовления новых образцов техники.

Расчет среднестатистического времени наработки до отказа ( или среднего времени безотказной работы ) по результатам наблюдений определяют по формуле:

где N – число элементов или изделий, подвергнутых наблюдениям или испытаниям; t – время безотказной работы i-го элемента (изделия).

Средняя наработка до отказа – это математическое ожидание наработки изделия до первого отказа. Следовательно, среднюю наработку до отказа можно определить по формулам:

- для непрерывной функции распределения надежности

- для дискретной функции надежности

Средняя наработка на отказ –это отношение наработки восстанавливаемого изделия к математическому ожиданию числа его отказов в течение этой наработки.

Статистическую оценку среднего значения наработки на отказ вычисляют как отношение суммарной наработки за рассматриваемый период испытаний или эксплуатации изделий к суммарному числу отказов этих изделий за тот же период времени:

Показатель наработки на отказ можно оптимизировать по экономическим критериям. На рис.7.3 показаны принципиальные зависимости затрат:

З_о - затраты на повышение времени наработки на отказ; З_э - затраты эксплуатационные; З_с - суммарные затраты.

Рис. 7.3. Общая модель экономически обоснованных норм

показателя надёжности T_о

Средняя наработка между отказами – это математическое ожидание наработки изделия от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа. Статистическую оценку среднего значения наработки между отказами вычисляют как отношение суммарной наработки изделия между отказами рассматриваемый период испытаний или эксплуатации к числу отказов этого (их) объекта(ов) за тот же период:

где m – число отказов за время t.

Интенсивность отказовλ(t) характеризует условную плотность вероятности возникновения отказов невосстанавливаемого изделия за рассматриваемый период времени в случае, если до этого их не наблюдалось

На практике при установлении статистического значения интенсивности отказов λ_с(t) пользуются формулой:

где N(Dt) – число отказавших изделий в интервале времени Dt;

N_cp - среднее число исправно работающих изделий в интервале Dt.

Интенсивность отказовλ(t) показывает, какая часть изделий становится неисправной за единицу времени работы по отношению к среднему числу исправно работающих изделий. Интенсивность отказов используется в качестве одного из основных критериев при оценке надежности изделий. На рис. 7.4. показано характерное изменение интенсивности отказов во времени для большинства промышленных изделий.

Рис. 7.4. Изменение интенсивности отказов во времени эксплуатации

Вероятность безотказной работы, выраженная через интенсивность отказов, имеет вид:

Это уравнение является одним из основных в теории и практике расчетов показатели надежности.

Параметр потока отказовλ₁(t) для восстанавливаемого изделия характеризуют плотность вероятности появления отказа ремонтопригодного объекта для определенного момента времени

где f(t) – плотность распределения потока отказов за период времени t.

При определении этого показателя статистическим методом имеем

где n(t) – количество отказов i-го изделия до наработки t;

n - число отказов изделия в интервале времени Dt.

Средняя частота отказов ω(t) показывает отношение числа отказавших изделий в единицу времени к числу испытываемых или наблюдаемых при условии, что отказавшие элементы изделий заменяются исправными или восстанавливаются, т.е.

Для качественного анализа безотказности работы изделия обычно принимают, что вероятность безотказной работы в период нормальной эксплуатации приближенно равна Р(t) = 1- λ(t). Дополнительными показателями безотказности служат коэффициенты технических простоев (η_пр) и исправности (η_испр). Коэффициент технических простоев (иначе говоря коэффициент неисправности), представляет собой отношение продолжительности простоев t_пр по причине неисправности техники за определенный промежуток времени к сумме продолжительности фактической работы t_ф и t_пр за тот же период времени:

Длительность исправной работы машины, характеризуемая коэффициентом исправности, рассчитывается по формуле:

Необходимо отметить, что в рассмотренных способах численных оценок показателей, связанных с отказами, не учитываются тяжести последствий от различных отказов. В большинстве случаев при определении показателей безотказности надо было бы установить критерий или коэффициент весомости отказов изделия, например, по экономическим последствиям восстановления работоспособности, исчерпанию ресурса и другим характеристикам работоспособности во времени.

Показатели безотказности в зависимости от целей управления качеством определяют на различных стадиях работы технического изделия. Например, наработку на отказ в период приработки изделия определяют для выявления ранних отказов с целью принятия необходимых мер по совершенствованию конструкции и технологии изготовления, исключающих причины появления ранних отказов серийно изготавливаемых изделий.

Во время производства техники показатели ее безотказности определяют через определенные промежутки времени, для контроля их нормируемых значений. На стадии эксплуатации оценивают безотказность с целью прогнозирования ее на интересующее время эксплуатации.

Инженер должен иметь в своем распоряжении методы измерения надежности, способы ее количественной оценки, позволяющие производить сравнительную количественную оценку, расчеты и испытания на надежность.

При написании выражений статистические показатели будем отмечать волнистой чертой сверху.

Вероятность безотказной работы объекта Р(t) – это вероятность того, что в пределах заданной наработки отказ объекта не возникает (наработка – продолжительность или объем работы).

Математическое определение:

где Т – случайное время (наработка) объекта до отказа;

t₃ – заданная наработка.

Другими словами, Р(t_з) есть вероятность того, что объект проработает безотказно в течение заданного времени t_з, начав работать в момент времени t=0.

Статистическое определение:

где N(0) – достаточно большое число одинаковых работоспособных объектов в момент времени t=0;

N(t₃) – число работоспособных объектов к моменту времени t₃.

Известно, что при N(0)→∞ статистическая оценка (t₃) сходится по вероятности к Р(t₃).

Вероятность Р(t₃) является монотонно убывающей функцией времени (см. рис. ), причем Р(0)=1 и Р(t₃=∞)=0, так как любой объект, работоспособный в момент включения, со временем откажет.

Вероятность отказа Q(t) –это вероятность того, что наработка объекта до отказа окажется меньше заданной наработки.

Математическое определение:

Статистическое определение:

Вероятность отказа объекта является функцией распределения наработки до отказа и в ряде случаев обозначается F(t₃). Очевидно, что Q(0)=0 и Q(t₃→∞)=1 (см. рис. ).

Рис. Пояснение статистического определения и

Рис. Зависимости P(t) и Q(t) от времени

Вероятность безотказной работы объекта на промежуточном интервале времени от t₁ до t₂ можно определить из соотношения

где P(t₁) и P(t₂) – вероятности безотказной работы объекта соответственно на интервале (0,t₁) и (0,t₂).

Вероятность безотказной работы объекта на интервале (t₁,t₂)

представляет собой условную вероятность безотказной работы объекта на интервале (t₁,t₂) при условии, что к моменту времени t₁ он был работоспособен.

Статистическое определение:

где N(t₁) и N(t₂) – соответственно число работоспособных объектов к моментам времени t₁ и t₂.

Плотность вероятности отказа f(t)- производная от вероятности отказа невосстанавливаемого объекта:

Из соотношения (9) следует, что f(t) характеризует скорость убывания вероятности безотказной работы, т. е. - это дифференциальный закон распределения .

Проинтегрировав соотношение (9), получим интегральный закон распределения

Статистическое определение:

характеризуется отношением числа отказавших в единицу времени невосстанавливаемых объектов к их первоначальному числу (в момент времени t=0).

Рис. К определению

Так как N(t)=N(0)·P(t) и N(t+∆t)=N(0)·P(t+∆t), то в пределе при

∆t→0 получим

Интенсивность отказов невосстанавливаемого объекта - λ(t) (лямбда от t) .

Математическое определение:

где f(t) – плотность вероятности отказа в момент времени t.

Ранее было показано:

Интегрируя левую и правую части (15) получим

Таким образом, имеем

Определим вероятность безотказной работы объекта на интервале (t₁,t₂)

(При делении экспонент показатели вычитаются.)

Статистическое определение:

характеризуется отношением числа отказавших в единицу времени невосстанавливаемых объектов к числу объектов работоспособных в начале интервала ∆t.

Интервал ∆t должен быть достаточно малым, чтобы обеспечить плавный характер кривой λ(t), и в то же время достаточно большим, чтобы на нем могли быть зафиксированы отказы объектов.

Нетрудно заметить, что при ∆t→0

Типовые зависимости P(t), f(t) и λ(t) для радиоэлектронных элементов показаны на рис.3.

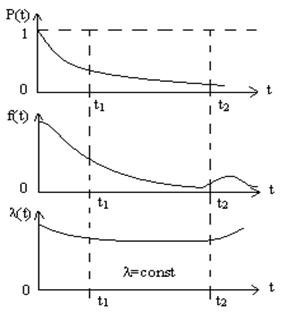
Рис.3. Типовые зависимости показателей надежности от времени.

Участок 0–t₁ характеризуется интенсивными отказами, вызываемыми скрытыми дефектами. Этот участок называется участком приработки. Участок при t>t₂ также характеризуется более интенсивными отказами. Эти отказы связаны со старением элементов, их механическим и электрическим износом. На участке от t₁ до t₂ преобладают случайные внезапные отказы; это участок нормальной работы, для которого обычно принимают интенсивность отказов λ(t)= λ=const.

Если λ(t)= λ, то из состояния (17) следует

Из соотношения (13) получим

При допущении постоянства интенсивности отказов говорят, что наработка до отказа распределена по экспоненциальному закону.

В таблице 1 показаны базовые значения интенсивности отказов для некоторых видов радиоэлектронных элементов.

Вид элемента	Интенсивность отказов, Е-6, 1/час
Конденсатор КСО	0,100
Полупроводниковый диод КД908	0,070
Дроссель	0,600
Кинескоп 61ЛК3Ц	7,300
Штепсельный разъем	3,000
Интегральная микросхема К155	0,160
Резистор СП3-35	0,050
Транзистор КТ965А	0,500
Трансформатор ТАН	0,200
Печатный проводник	0,010
Точка пайки	0,010

Средняя наработка до отказа –математическое ожидание наработки объекта до отказа.

из соотношения (25)

т.е. Т_ср численно равна площади под кривой Р(t).

С учетом (7) из соотношения (26) получим

Если λ(х)= λ=const, то средняя наработка до отказа

т.е. при экспоненциальном законе надежности средняя наработка объекта обратно пропорциональна интенсивности отказов, а интенсивность отказов обратно пропорциональна средней наработке.

Принимая во внимание соотношение (28), из формул (22) и (24) получим

Выясним смысл Т_{ср .}

т.е. под средней наработкой до отказа можно понимать такую наработку, по которой из множества одинаковых объектов в среднем должны остаться работоспособными 37%.

Основными качественными показателями надежности является:

- вероятность безотказной работы;

- средняя наработка до отказа.

Интенсивность отказов l(t) - это число отказавшихn(t) элементов устройства в единицу времени, отнесенное к среднему общему числу элементов N(t), работоспособных к моменту времени Δt[ 9]

l (t)=n(t)/(Nt*Δt),

где Δt - заданный отрезок времени.

Например: 1000 элементов устройства работали 500 часов. За это время отказали 2 элемента. Отсюда,

l (t)=n(t)/(Nt*Δt)=2/(1000*500)=4*10 -6 1/ч, то есть за 1 час может отказать 4-е элемента из миллиона.

Показатели интенсивности отказов l(t) элементов являются справочными данными, в приложении Г приводятся интенсивности отказов l(t)для элементов, часто применяемых в схемах.

Электротехническое устройство состоит из большого числа комплектующих элементов, поэтому определяют эксплуатационную интенсивность отказов l(t) всего устройства как сумму интенсивностей отказов всех элементов, по формуле [ 11]

где k – поправочный коэффициент, учитывающий относительное изменение средней интенсивности отказов элементов в зависимости от назначения устройства;

m – общее количество групп элементов;

n_і - количество элементов в і- й группе с одинаковой интенсивностью отказов l_і(t) .

Вероятность безотказной работы P(t) представляет собой вероятность того, что в пределах указанного периода времени t, отказ устройства не возникнет. Этот показатель определяется отношение числа устройств, безотказно проработавших до момента времени t к общему числу устройств, работоспособных в начальный момент.

Например, вероятность безотказной работы P(t) =0,9 представляет собой вероятность того, что в пределах указанного периода времени t= 500час, отказ произойдет в (10-9=1) одном устройстве из десяти, и из 10 устройств 9 будут работать без отказов.

Вероятность безотказной работы P(t) =0,8 представляет собой вероятность того, что в пределах указанного периода времени t=1000час, отказ произойдет двух 2 устройствах из ста, и из 100 устройств 80 устройств будут работать без отказов.

Вероятность безотказной работы P(t) =0,975 представляет собой вероятность того, что в пределах указанного периода времени t=2500час, отказ произойдет в 1000-975=25 устройствах из тысячи, а 975 устройств будут работать без отказов.

Количественно надёжность устройства оценивается как вероятность P(t) события, заключающегося в том, что устройство в течение времени от 0 до t будет безотказно выполнять свои функции. Величина P(t) вероятность безотказной (рассчитанное значение Р(t) не должно быть менее 0,85) работы определяется выражением

(10.1)

где t – время работы системы, ч (t выбирается из ряда: 1000, 2000, 4000, 8000, 10000 ч.);

λ – интенсивность отказов устройства, 1 /_ч;

Т₀ – наработка на отказ, ч.

Расчёт надёжности заключается в нахождении общей интенсивности отказов λ устройства и наработки на отказ:

. (10.2)

Время восстановления устройства при отказе включает в себя время поиска неисправного элемента, время его замены или ремонта и время проверки работоспособности устройства.

Среднее время восстановления Т_в электротехнических устройств может выбираться из ряда 1, 2, 4, 6, 8, 10, 12, 18, 24, 36, 48 час. Меньшие значения соответствуют устройствам с высокой ремонтнотпригодностью. Среднее время восстановления Т_в можно уменьшить используя встроенный контроль или самодиагностику, модульное исполнение составных частей, доступный монтаж.

Значение коэффициента готовности определяется по формуле

где Т₀ – наработка на отказ, ч.

Т_в – среднее время восстановления, ч.

Надёжность элементов в значительной степени зависит от их электрических и температурных режимов работы. Для повышения надёжности элементы необходимо использовать в облегченных режимах, определяемых коэффициентами нагрузки.

Коэффициент нагрузки – это отношение расчетного параметра элемента в рабочем режиме к его максимально допустимому значению. Коэффициенты нагрузки различных элементов могут сильно отличаться.

При расчёте надежности устройства все элементы системы разбиваются на группы элементов одного типа и одинаковыми коэффициентами нагрузки К_н.

Интенсивность отказа і- го элемента определяется по формуле

(10.3)

где К_{н і} - коэффициент нагрузки, рассчитывают в картах рабочих режимов, либо задают полагая, что элемент работает в нормальных режимах, в приложении Г приводятся значения коэффициентов нагрузки элементов;

λ _0і – базовая интенсивность отказов і - го элемента приводится в приложении Г.

Часто, для расчета надежности, используются данные интенсивности отказа λ _0і аналогов элементов.

Пример расчета надежности устройства состоящего из покупного комплекса BT-85W импортного производства и разрабатываемого на элементной базе серийного производства источника питания.

Интенсивности отказов изделий импортного производства определяют, как обратную величину времени эксплуатации, (иногда берут гарантийный срок обслуживания изделия) из расчета эксплуатации в одни сутки определенного числа часов.

Гарантийный срок службы покупного импортного изделия 5 лет, изделие будет работать 14,24часа в сутки:

Т=14,24час х 365дней х 5 лет = 25981 часов – время наработки на отказ.

10 -6 1/час - интенсивность отказов.

Расчёты и исходные данные выполняют на ЭВМ с использованием программ Excel и приводятся в таблицах 10.1 и 10.2. Пример расчета приводится в таблице 10.1.

Таблица 10.1 – Расчет надежности системы

Наименование и тип элемента или аналога	Коэффи-циент, нагрузки, К_н_i
λ_i *10 -6 , 1 /_ч	λ_i К_н_i10 -6 1 /_ч	Кол-во n_i,	n_і λ_i 10 -6 , 1 /_ч
Комплекс BT-85W	1,00	38,4897	38,4897	38,4897
Конденсатор К53	0,60	0,0200	0,0120	0,0960
Розетка (вилка)СНП268	0,60	0,0500	0,0300	0,0900
Микросхема TRS	0,50	0,0460	0,0230	0,0230
Резистор ОМЛТ	0,60	0,0200	0,0120	0,0120
Вставка плавкая ВП1-1	0,30	0,1040	0,0312	0,0312
Стабилитрон 12В	0,50	0,4050	0,2500	0,4050
Индикатор 3Л341Г	0,20	0,3375	0,0675	0,0675
Кнопочный выключатель	0,30	0,0100	0, 0030	0,0030
Фотодиод	0,50	0,0172	0,0086	0,0086
Соединение сваркой	0,40	0,0001	0,0004	0,0004
Провод, м	0,20	0,0100	0,0020	0,2	0,0004
Соединение пайкой	0,50	0,0030	0,0015	0,0045
l всего устройства	å=39,2313

Определяем общую интенсивность отказов устройства

Тогда наработка на отказ согласно выражению (10.2) и соответственно равна

Для определения вероятности безотказной работы за определенный промежуток времени построим график зависимости:

Таблица 10.2 - Расчет вероятности безотказной работы

t(час)
P(t)	0,97	0,9	0,8	0,55	0,74	0,65	0,52	0,4	0,34

График зависимости вероятности безотказной работы от времени работы показан на рисунке 10.1.

Рисунок 10.1 – Вероятность безотказной работы от времени работы

Для устройства, как правило задают вероятность безотказной работы от 0,82 до 0,95. По графику рисунка 10.1 можем определить для разработанного устройства при заданной вероятности безотказной работы Р(t)=0,82, время наработки на отказ Т_о=5000час.

Расчет выполнен для случая, когда отказ любого элемента приводит к отказу всей системы в целом, такое соединение элементов называется логически последовательным или основным. Надежность можно повысить резервированием.

Например. Технология элементов обеспечивает среднюю интенсивность отказов элементарных деталей l_i=1*10 -5 1/ч. При использовании в устройстве N=1*10 4 элементарных деталей суммарная интенсивность отказов lо= N*li=10 -1 1/ч. Тогда среднее время безотказной работы устройства To=1/lо=10 ч. Если выполнить устройство на основе 4-х параллельно включенных одинаковых устройств, то среднее время безотказной работы увеличится в N/4=2500 раз и составит 25000 ч. или 34 месяца или около 3 лет.

Формулы позволяют выполнить расчет надежности устройства, если известны исходные данные - состав устройства, режим и условия его работы, интенсивности отказов его элементов.

В последнее время мне довольно много приходится работать с расчетами надежности и рисков, и в этой статье я постараюсь восполнить этот пробел, отталкиваясь от своего предыдущего материала (из цикла о машинном обучении) о пуассоновском случайном процессе и подкрепляя текст вычислениями в Mathcad Express, повторить которые вы сможете скачав этот редактор (подробно о нем тут, обратите внимание, что нужна последняя версия 3.1, как и для цикла по machine learning). Сами маткадовские расчеты лежат здесь (вместе с XPS- копией).

1. Теория: основные характеристики отказоустойчивости
Вроде бы, из самого определения (Mean Time To Failure) понятен его смысл: сколько (конечно, в среднем, поскольку подход вероятностный) прослужит изделие. Но на практике такой параметр не очень полезен. Действительно, информация о том, что среднее время до отказа жесткого диска составляет полмиллиона часов, может поставить в тупик. Гораздо информативнее другой параметр: вероятность поломки или вероятность безотказной работы (ВБР) за определенный период (например, за год).

Для того чтобы разобраться в том, как связаны эти параметры, и как, зная MTTF, вычислить ВБР и вероятности отказа, вспомним некоторые сведения из математической статистики.

Оба параметра — это интервальные характеристики отказоустойчивости, т.к. речь идет о вероятности отказа (или наоборот, безотказной работы) на интервале (0,t). Если отказ рассматривать, как случайное событие, то, очевидно, что Q(t) — это, по определению, его функция распределения. А точечную характеристику можно определить, как
p(t)=dQ(t)/dt = плотность вероятности, т.е. значение p(t)dt равно вероятности, что отказ произойдет в малой окрестности dt момента времени t.

И, наконец, самая важная (с практической точки зрения) характеристика: λ(t)=p(t)/P(t)=интенсивность отказов.
Это (внимание!) условная плотность вероятности, т.е. плотность вероятности возникновения отказа в момент времени t при условии, что до этого рассматриваемого момента времени t изделие работало безотказно.

Измерить параметр λ(t) экспериментально можно путём испытания партии изделий. Если к моменту времени t работоспособность сохранило N изделий, то за оценку λ(t) можно принять процент отказов в единицу времени, происходящих в окрестности t. Точнее, если в период от t до t+dt откажет n изделий, то интенсивность отказов будет примерно равна
λ(t)=n/(N*dt).

Именно эта λ-характеристика (в пренебрежении ее зависимостью от времени) и приводится чаще всего в паспортных данных различных электронных компонент и самых разных изделий. Только сразу возникает вопрос: а как вычислить вероятность безотказной работы и при чем здесь среднее время до отказа (MTTF).

2. Экспоненциальное распределение
В терминологии, которую мы только что использовали, пока не было никаких предположений о свойствах случайной величины — момента времени, в который происходит отказ изделия. Давайте теперь конкретизируем функцию распределения значения отказа, выбрав в качестве нее экспоненциальную функцию с единственным параметром λ=const (смысл которого будет ясен через несколько предложений).

Дифференцируя Q(t), получим выражение для плотности вероятности экспоненциального распределения:
,
а из него – функцию интенсивности отказов: λ(t)=p(t)/P(t)=const=λ.

Что мы получили? Что для экспоненциального распределения интенсивность отказов – есть величина постоянная, причем совпадающая с параметром распределения. Этот параметр и является главным показателем отказоустойчивости и его часто так и называют λ-характеристикой.

Мало того, если теперь посчитать среднее время до первого отказа – тот самый параметр MTTF (Mean Time To Failure), то мы получим, что он равен MTTF=1/ λ.

надежность элементов можно оценить одним числом, т.к. λ=const;
по известной λ довольно просто оценить остальные показатели надежности (например, ВБР для любого времени t);
λ обладает хорошей наглядностью
λ нетрудно измерить экспериментально

Но это еще не все, потому, что для экспоненциального распределения особенно легко делать расчет систем, состоящих из множества элементов. Но об этом – в следующей статье (продолжение следует).

Читайте также: