В чем измеряется лямбда
Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.
Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…
λ-исчисление: основные понятия
Синтаксис
В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.
Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.
Термы:
| переменная: | x |
| лямбда-абстракция (анонимная функция): | λx.t , где x — аргумент функции, t — её тело. |
| применение функции (аппликация): | f x , где f — функция, x — подставляемое в неё значение аргумента |
- Применение функции левоассоциативно. Т.е. s t u — это тоже самое, что (s t) u
- Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е. λx. λy. x y x означает то же самое, что λx. (λy. ((x y) x))
- Скобки явно указывают группировку действий.
Процесс вычисления
Рассмотрим следующий терм-применение:
Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:
который для простоты можно переписать как
(напомним, что id — это функция тождества вида λx.x )
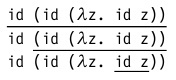
В этом терме содержится три редекса:
Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение
(λx.λy. x) z ((λx.x x)(λx.x x))
Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y . Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y , а z — первоначальный терм имел бы вид (λx.λz.x)y и после редукции выглядел бы как λz.y . Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.
Так же бывает, что у нас есть абстракция λx.t x , причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t . Такое преобразование называется η-конверсией.
На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

В очередном опусе Итана Сигеля резанула фраза
Пронаблюдав за удалёнными сверхновыми и измерив, как Вселенная расширялась миллиарды лет, астрономы обнаружили нечто удивительное, загадочное и неожиданное.
By observing distant supernovae and measuring how the Universe had expanded over billions of years, astronomers discovered something remarkable, puzzling and entirely unexpected
О какой неожиданности может идти речь? Там ведь совершенно шикарная история длиной в 80 лет с яркими открытиями и закрытиями. История про то, как на самом деле делается настоящая наука. История скорее про физиков, чем про физику.
О чём вообще весь сыр-бор?
Первую версию Общей Теории Относительности (ОТО) Альберт Эйнштейн представил публике 25 ноября 1915 года. В оригинале уравнения ОТО Эйнштейна выглядели вот так:

или, в современной записи, вот так:

Для неумеющего в тензоры читателя понятнее уравнение (1) в оригинальной записи Эйнштейна. Там написано, что энергия-импульс материи G равен кривизне пространства R плюс тензор Риччи S. (Этот самый тензор Риччи тоже есть кривизна, только в более другой форме).
Сейчас, решая уравнение ОТО, энергию-импульс обычно считают известным, а ищут как раз кривизну. Поэтому в современной записи стороны уравнения поменяли местами. Заодно поменяли буковки: G → T, S → Rμν.
Откуда есть пошла лямбда
Но физика — это вам не математика. Здесь нельзя взять формулу и напихать в неё добавочных слагаемых просто так. Нужно иметь очень веские основания, и теоретические, и экспериментальные.
Хотя ниже вы увидите, насколько мало Эйнштейн знал о Вселенной в те годы, но тогда, в 1916, такие основания у него были. Альберт Германович точно знал, что звёзды не попадали друг на друга и совершенно не собираются этого делать в обозримом будущем. Однако, в ОТО-1915 было только притяжение, которое нужно было чем-то сбалансировать.
Первое физическое толкование смысла лямбды
В такой трактовке ненулевое значение Λ означает, что наша Вселенная искривлена сама по себе, в том числе и при отсутствии какой-либо гравитации. Ну, вот такой нам достался мир. Однако, большинство физиков в это не верят, и считают, что у наблюдаемого искривления должна быть какая-то внутренняя причина. Какая-то неведомая доселе фигня, которую можно открыть.
На сегодняшний день измеренная кривизна пространства Вселенной таки равна нулю, но с очень паршивой точностью, порядка 0.4%. И не очень-то видно способов эту точность улучшить.
С измерениями кривизны есть две концептуальные проблемы.
Первая в том, что мы не можем измерить совсем пустое пространство, потому что просто ничего там не видим. А если там есть что-то, что мы таки видим, то пространство уже не пустое и, значит, уже дополнительно искривлено гравитацией.
Допустим, у нас есть как-то измеренные координаты объектов, плюс пачка фотографий этих объектов в разных ракурсах (снятых из разных точек). Тогда мы можем вычислить кривизну пространства. Например, гравитация Солнца отклоняет пролетающий мимо свет далёких звёзд. Во время солнечных затмений это отклонение можно измерить экспериментально и сравнить с предсказаниями ОТО.
Теперь наоборот: допустим, мы знаем кривизну пространства, и у нас есть пачка фотографий. Тогда, если кривизна достаточно хорошая, без чёрных дыр и т.п. — мы можем вычислить координаты объектов на фото. Именно так работают наши глаза, точнее мозги, когда вычисляют расстояние до объектов по двум фоткам с разных точек.
Поэтому измерить кривизну наблюдаемой Вселенной в целом мы можем только из очень окольных соображений.
Вселенная Фридмана
Meanwhile in Russia, не смотря на войны и революции, над теорией ОТО бился прапорщик (и по совместительству профессор) Александр Александрович Фридман. Он рассмотрел все варианты лямбд и выяснил следующее:
При Λ < 0 имеют место лишь силы притяжения, как гравитационные, так и вызванные кривизной впуклоговогнутого пространства. Рано или поздно звёзды и галактики в таком мире таки попадают друг на друга. Причём конец будет неожиданно быстрым и очень горячим.
Но самое интересное происходит при Λ = 0. Здесь всё зависит от начальных условий — т.е. координат и скоростей конкретных галактик. Возможны три варианта: большое сжатие, большой разлёт и стационарный вариант, когда галактики разлетаются, но с относительно небольшими скоростями и без ускорения.
Сегодня вышеописанные ситуации называются космологическими решениями Фридмана.
Статьи Фридмана 1922 и 1924 годов отменяли необходимость в лямбда-члене, из-за чего поначалу были приняты Эйнштейном в штыки.
За свою работу Фридман вполне мог претендовать на Нобелевку.
Летом 1925 он женился, поехал в свадебное путешествие в Крым, съел там немытую грушу, заразился тифом и в сентябре — умер.
И да, статья Итана про примерно такой график (конкретно на этом учтены данные на 2010 год):

Здесь по горизонтали отложено z — это красное смещение, по вертикали наблюдаемая яркость сверхновых особого типа Ia, которые всегда выделяют одно и то же количество энергии. Вообще, это два способа измерения одного и того же расстояния, но, так сказать, в разные моменты времени.
Серые палки — наблюдавшиеся события с их погрешностью измерений. Синим пунктиром отложено предсказание при Λ = 0, красной линией — аппроксимация фактически наблюдаемых значений. Отклонение красной линии от прямой означает, что Вселенная расширяется ускоренно. Но Эйнштейн об этом так и не узнал.
Вселенная Каптейна
Перейдём к экспериментальной части.
Голландский астроном Якобус Корнелиус Каптейн открыл звезду Каптейна в 1897, после чего приступил к opus magnum всей своей жизни. Объединяя огромное количество наблюдений разных обсерваторий, он попытался создать первую карту Вселенной. По его карте выходило, что вселенная имеет форму вращающегося (sic!) диска крышесносящего по тем временам размера 40000 световых лет, причём Солнце находится отнюдь не в центре, а вполне себе на задворках. Закончена и опубликована эта работа была только в 1922.
Для понимания уровня тогдашних знаний: то, что Каптейн считал невероятно огромной Вселенной, сегодня считается совершенно рядовой, ничем не примечательной среди миллиардов таких же… галактикой Млечный Путь. Тем не менее, заслуга Каптейна в том, что он открыл её вращение и приблизительно вычислил её центр.
Наблюдения Хаббла (астронома, а не телескопа)
Статью со своими открытиями, из которой следовало, что Вселенная значительно больше, чем наш Млечный путь, Хаббл представил американскому астрономическому обществу первого января 1925. За что и был освистан страдающими от похмелья коллегами, едва свыкшимися с расстояниями Каптейна.
Хаббл не унимался и прикрутил к телескопу ещё и спектрометр. Анализируя красное смещение галактик, он выяснил, что галактики разбегаются, а Вселенная, соответственно, расширяется. Заодно он открыл закон имени себя с константой имени себя (впрочем, закон был предсказан Леметром), и описал всё это в статьях к концу 20-ых годов. Согласно его наблюдениям, оказалась верна модель Фридмана для Λ = 0.
Это выбило из-под лямбды теперь уже и экспериментальные основания её существования.
Здесь ещё нужно упомянуть, что первоначальные оценки Хаббла были очень уж неточными и показывали возраст Вселенной порядка 2 миллиардов лет. Позднее это войдёт в противоречие с данными геофизиков, которые при помощи радиоизотопного анализа оценят возраст Земли в несколько миллиардов лет, и десятилетиями будет сильнейшей головной болью для физиков-космологов.
Стационарная Вселенная Хойла
С начала 30-ых годов вопрос с лямбдой считался решённым, и из мейнстримных физиков ей никто толком не занимался. Одним из редких исключений, рискнувших попереть супротив самого Эйнштейна, стал британец Фред Хойл.
Речь пойдёт о гелии. Этот элемент феноменально инертен и не хочет ни с чем реагировать. Причём не только химически, но и физически тоже, если мы говорим про гелий-4. Его ядро — альфа частица — имеет пиковую энергию связи на нуклон в своей области. см. рис из какого-то реферата:

Это значит, что альфа-частица не может присоединить дополнительные протоны или другую альфа-частицу иначе как случайно: это просто-напросто энергетически невыгодно. А в ядрах звёзд ничего кроме протонов и альфа-частиц и нет.
Возникал резонный вопрос: а откуда, собственно, взялись химические элементы тяжелее гелия?
Ближайшее ядро, в которое может превращаться гелий-4, это углерод-12. Но для этого нужно объединить три альфа-частицы.
Проблема в том, что вероятность столкновения трёх альфа-частиц одновременно слишком мала. А двухшаговый процесс (сначала сталкиваются две частицы, потом очень быстро, пока они не разлетелись обратно на две альфа-частицы, в них врезается ещё одна), в принципе, возможен, но расчёты Эдвина Солпитера показывали, что такой процесс идёт слишком вяло, чтобы производить существенные количества углерода.
Однако, по расчётам Хойла выходило, что при наличии такого уровня в три-альфа процессе наступает резонанс, и звёзды — красные гиганты производят достаточно много углерода для нашего существования.
Удивительно, но американцы решили провести небольшой эксперимент на своём ускорителе. И да — триумфально нашли нужный энергетический уровень на 7.65 МэВ, который физики-ядерщики всего мира почему-то проглядели во всех предыдущих экспериментах.
Сегодня такое возбуждённое состояние углерода-12, когда три альфа-частицы фактически выстраиваются по линии, называется хойловским. Соответствующая статья Хойла, Фаулера и супругов-астрономов Джефри и Маргерит Бёрбиджей является краеугольным камнем современных теорий звёздного нуклеосинтеза и настолько часто цитируется, что обозначается просто B²FH, без ссылок и расшифровок.
И — да, на сегодня это чуть ли не единственное известное успешное предсказание на основе антропного принципа.
Однако, из квантовых флуктуаций постоянно рождается новое вещество, причём так, что средняя плотность материи остаётся одинаковой. Расчёты показывают, что в одном кубическом километре пространства должен рождаться всего-навсего один протон раз в 300000 лет (а так же один электрон или что-то типа того для сохранения электрического заряда). Прекрасное число, чтобы исключить любую возможность какой-либо экспериментальной проверки!
Теория стационарной Вселенной серьёзно рассматривалась как альтернатива теории Большого Взрыва в 50-х и начале 60-х. Но экспериментальное открытие в 1964 году предсказанного ТББ реликтового излучения поставило на ней крест.
За статью B²FH дали Нобелевку. Но только Фаулеру, который распорядился провести десятидневный эксперимент. Ни супругам Бёрбиджам, проводившим длительные астрономические наблюдения и собственно написавшим статью, ни автору идеи Хойлу нобелевку не дали — за упорствование в космологической ереси.
Квантовая лямбда
Вернёмся к уравнению ОТО.
Слева (в современной записи) стоит кривизна пространства, сиречь гравитация по ОТО. Справа — тензор энергии-импульса. Под этим тензором стоит жутко сложный матан, но суть в следующем: там учтена вся-вся-вся материя Вселенной во всех видах и состояниях. И обычное вещество, и всякие хитрые частицы, и все виды излучений (кроме гравитации, которая слева).
Теперь мысленно перенесём лямбду вправо. В такой записи это будет не дополнительная кривизна, а какая-то неучтённая энергия (замечу, отрицательная, раз уж мы считаем лямбду положительной). И здесь просматриваются две возможности.
Первая гипотеза состоит в том, что лямбда — это энергия собственно вакуума. Звучит диковато, но на самом деле вполне согласуется с квантовой механикой. Возьмём кусок пространства и уберём из него всё, что хотя бы в принципе можно убрать. Уберём всё вещество, все частицы и все волны, независимо от их природы. Останутся только физические поля в невозмущённом состоянии. Полный штиль.
Так вот, у некоторых полей (например, Хиггсовских) в пустоте ненулевое значение. И теоретически у них есть некоторая энергия. Кроме того, в силу принципа неопределённости у любых полей есть квантовые флуктуации — и они тоже имеют некоторую энергию.
Вместо заключения
Длина волны - это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл - это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
На рисунке показаны основные параметры волны, используемые в физике:
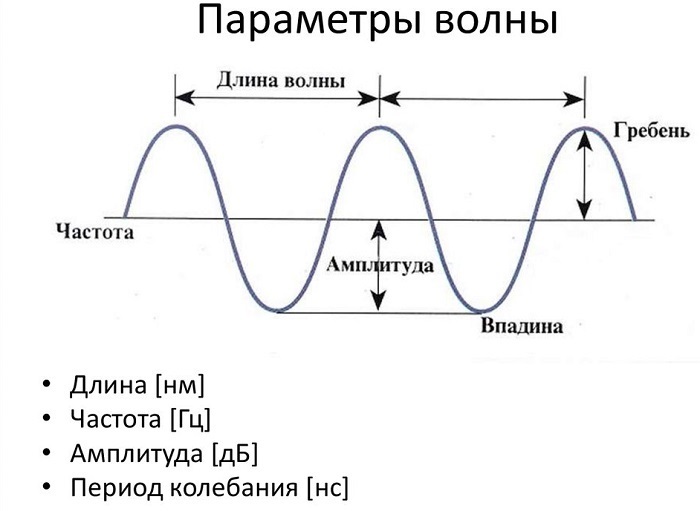
Определение и формула длины волн
Волна - это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
Греческая буква "λ" (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая - высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
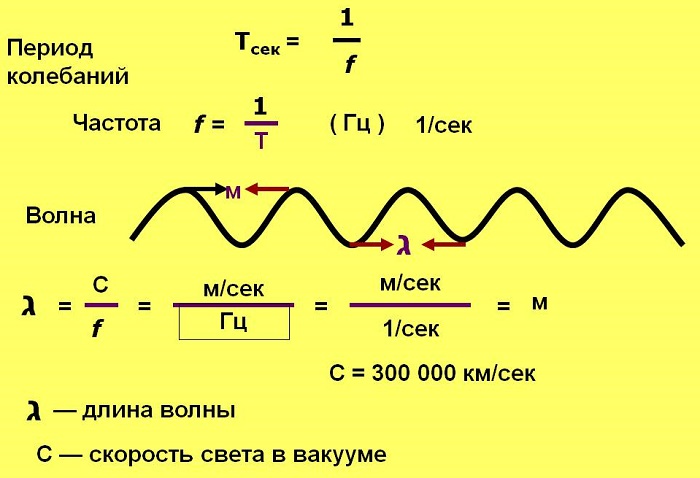
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 10 8 м/с поделить на длину в метрах.
Единицы измерения длины волны λ - нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).
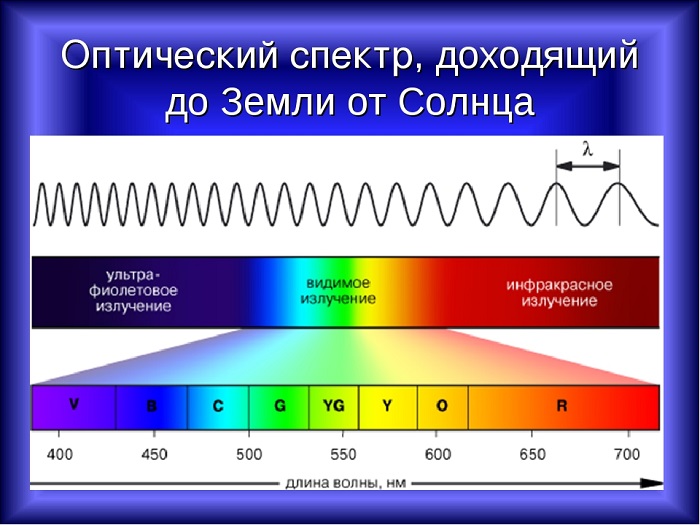
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
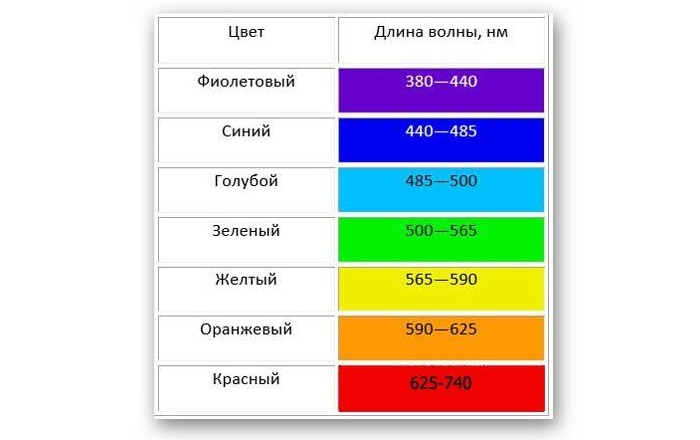
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной - красный, который составляет около 700 нм.
Таблица показывает длину волны в зависимости от цвета:
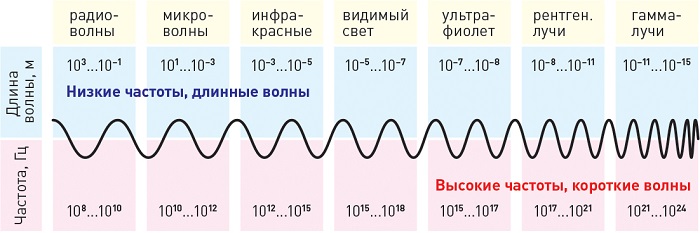
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

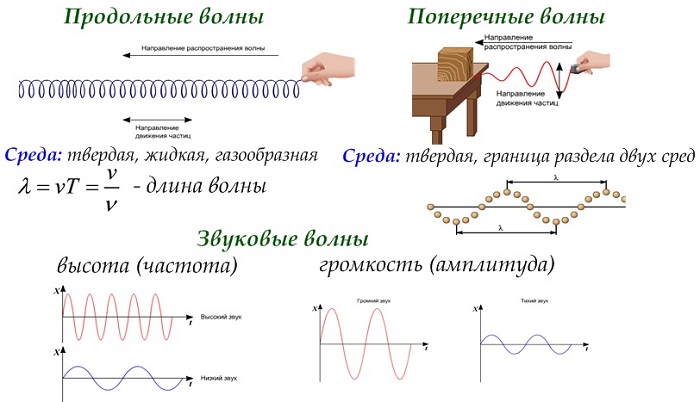
Морские волны — далеко не все примеры волн. И длина волны — это не серферская характеристика, а вполне себе физическая величина. Сегодня разберемся, что такое волна и как ее охарактеризовать.
О чем эта статья:
Волна: продольная и поперечная
Начнем с того, что волна — это распространение колебания в пространстве.
Волны бывают механическими и электромагнитными.
Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.
- Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.
Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.
Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.
Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.
Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.
Электромагнитные волны — это те волны, которые мы потрогать не можем.
Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 10 8 м/с. И источники у них разные.
Волны также принято делить на продольные и поперечные:

Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.
- Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.
Поперечные — волны, у которых колебание происходит поперек направления распространения волны.
- Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
- Видимый свет и дрожание гитарной струны — тоже поперечные волны.
На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.
Длина волны: определение и расчет
Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.
Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.
Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.
Формула периода колебания волны
T = t/N
N — количество колебаний [—]
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Связь со скоростью
Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).
Формула скорости
𝑣 = S/t
Переходя к волнам, можно провести следующие аналогии:
А для скорости даже аналогия не нужна — скорость и в Африке скорость.
Формула скорости волны
𝑣 = λ/T
λ — длина волны [м]
Задачка
Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
Решение:
Возьмем формулу скорости:
Резонанс
Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.
На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.

Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.
Формула частоты
ν = N/t
N — количество колебаний [—]
В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂
Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.
В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова фаллический (прилагательное):
Синонимы к слову «лямбда»
Предложения со словом «лямбда»
Начальная функция масс (НФМ) является эмпирической функцией, описывающей распределение масс звёзд в элементе объёма с точки зрения их начальной массы (масса с которой они сформировались). Свойства и эволюция звёзд тесно связаны с их массой, поэтому НФМ является важным предсказательным инструментом для астрономов при изучении большого количества звёзд. НФМ относительно инвариантна для похожих групп звезд. Важным является предположение о единстве, универсальности НФМ для всей Галактики или, по крайней.
Функция масс двойных звёзд (англ. Binary mass function) — функция, создающая ограничения для массы ненаблюдаемого компонента (звезды или экзопланеты) в спектрально-двойных звёздах или планетных системах с одной линией. Значение определяется по наблюдаемым характеристикам: по орбитальному периоду двойной системы и пику лучевой скорости наблюдаемой звезды. Скорость одного компонента двойной и орбитальный период двойной системы предоставляют частичную информацию о расстоянии и гравитационном взаимодействии.
Симбиотические звёзды — небольшой класс двойных звезд, имеющих сложные спектры, где наряду с полосами поглощения TiO имеются эмиссионные линии. В их спектрах были обнаружены линии, характерные для туманностей (ОIII, NeIII и т. п.), линии однократно ионизованных металлов, а также запрещённые линии высокой ионизации (например: FeVIII). Все известные к настоящему моменту времени симбиотические звёзды являются переменными с периодами в несколько сотен дней.
Затме́нные звёзды (затме́нные переме́нные, затме́нные двойны́е, фотометри́ческие двойны́е) — звездные системы, в которых наблюдается периодическое изменение блеска вследствие затмений одной звезды другой.
Переменные звезды имеют специальные обозначения, если они ещё не были обозначены буквой греческого алфавита, в формате обозначения Байера, в сочетании с именем созвездия в родительном падеже, в котором эта звезда находится. (см. Список созвездий и их латинское название (родительный падеж)).
Читайте также:

