Как определить направление линии зуба косозубого колеса

Обновлено: 05.06.2026

пор, пока эвольвентный профиль не придет в соприкосновение с профилем сопряженного колеса.

Для данного межосевого расстояния и диаметров основных окружностей угол зацепления можно определить из выражения

Угол зацепления у прямозубого цилиндрического колеса имеет место только в плоскости, перпендикулярной к оси колеса. У косозубого колеса углы зацепления расположены в трех плоскостях.

Торцовый угол зацепления расположен в плоскости, перпендикулярной к оси вращения колеса, или параллельно торцу колеса. Нормальный угол зацепления расположен в плоскости, перпендикулярной линии зубьев, расположенных наклонно к оси колеса. Этот угол используется в расчетах и чертежах зубчатых колес. В плоскости оси вращения колеса угол зацепления называют осевым. Углы в этой плоскости используют, например, у червяков, которые имеют большой угол подъема винтовой линии. Практически угол зацепления пары зубчатых колес выбирается конструктором исходя из назначения зубчатой передачи. Обычно зубчатые колеса с эвольвентным профилем имеют углы зацепления в пределах от 14,5 до 30°. Стандартные прямозубые цилиндрические колеса, как правило, изготовляют с углом зацепления 20°. Нормальный угол зацепления косозубых колес берется в пределах an = 14,5°-4-18,5°, а иногда 20°. Большие углы зацепления (25- 30°) используют в зубчатых колесах насосов. С увеличением угла зацепления прочность зубьев повышается, уменьшение угла зацепления способствует снижению уровня шума.

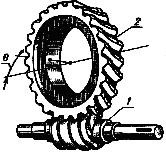
Углом наклона линии зуба f> называют острый угол, заключенный между осью вращения колеса и касательной к направлению линии зуба на делительной поверхности (рис. 24). Косозубые колеса могут быть с правым и левым направлением линии зуба. Два сопряженных косозубых колеса имеют зубья с разным направлением, например одно колесо имеет правое направление линии зуба, другое левое и наоборот.

Если смотреть на зубчатое колесо вдоль его оси вращения, и зуб колеса при своем продолжении удаляется от оси в направлении по часовой стрелке, то такое колесо имеет правое направление линии зуба (рис. 24, а). Если зуб колеса при своем продолжении удаляется в направле-

Рис. 24. Направление угла наклона линии зуба косозубого колеса:

а - правое б - левое

направление зуба; направление зуба

2 Кглашннког С. И.

НИИ против часовой стрелки, то такое колесо имеет левое направление линии зуба (рис. 24, б).

Окружностью вершин называют окружность, описанную вокруг центра колеса и ограничивающую вершины головок еубьев (рис. 21)

Окружностью впадин df называют окружность, описанную вокруг центра колес и ограничивающую впадины зубьев.

Высотой головки зуба называют часть зуба, расположенную над делительной окружностью.

Высотой ножки зуба hf называют часть зуба, расположенную под делительной окружностью.

Высота зуба h равна сумме высот головки и ножки зуба, включая закругление в основании зуба.

У некорригированных зубчатых колес высота головки равна модулю, а высота ножки зуба равна 1,25т. Величина 0,25т соответствует радиальному зазору в паре.

Полная высота зуба должна обеспечивать достаточный радиальный зазор, с тем чтобы вершина головки зуба сопряженного колеса свободно вращалась во впадине. Если во впадине зуба предусмотрено закругление (переходная поверхность), которое обеспечивается радиусом при вершине зуба червячной фрезы, контроль за сохранением полной высоты зуба при изготовлении должен быть более тщательным, чтобы предотвратить заклинивание головки во впадине зубьев сопряженного колеса. Когда требуется полностью закругленная впадина зуба колеса, то полная высота зуба увеличивается по отношению к стандартной высоте.

Высоту профиля зуба червячной фрезы для обработки под шевингование рекомендуется сохранить полностью. Радиус закругления / и дополнительную высоту зуба определяют, как показано на рис. 25.

Закругленная высота зуба увеличивает период стойкости инструмента и повышает прочность зубьев колеса.

Окружной толш,иной зуба называют длину дуги делительной окружности d, ограниченную боковыми сторонами профиля зуба (рис. 26).

Толщиной зуба по хорде делительной окружности s называют величину хорды, которая стягивает дугу делительной окружности, расположенную между боковыми сторонами профиля зуба. Толщина зуба по хорде делительной окружности s и высота головки зуба до хорды Ra используются для контроля размера зуба по штангензубомеру (рис. 26). У прямозубых колес контроль производят в торцовом сечении, у косозубых - в нормальном.

Высота головки зуба до хорды рассчитывается от теоретического диаметра вершин зубьев d, поэтому перед контролем размера зубьев необходимо измерить фактический диаметр вершин зубьев проверяемого колеса. Разницу между фактическим и теоретическим диаметром заготовки следует учитывать изменением высоты головки зуба до хорды. Если фактический диаметр за-

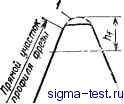
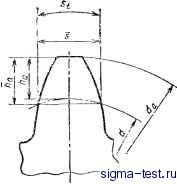
Рис. 25. Форма зуба червячной фрезы Д.ПЯ обеспечения закруг.пенной впадины зуба ко.песа

Рис. 26. Размеры зуба по штангензубо-меру

ГОТОВКИ больше теоретического, то половину разницы в диаметрах прибавляют к высоте головки до хорды. Когда фактический диаметр заготовки меньше теоретического, высота головки зуба до хорды соответственно уменьшается. Этот метод контроля размера зуба широко применяют при изготовлении небольших партий зубчатых колес, ремонтном деле и т. д.

Обычно хордальная толщ,ина зуба несколько уменьшается для получения бокового зазора между зубьями. Иногда путем соот-ветствующ,его изменения толщин зубьев колеса и шестерни достигается их равная прочность.

Боковой зазор / - кратчайшее расстояние между нерабочими профилями зубьев, когда рабочие профили зубьев находятся в зацеплении (рис. 27). У косозубых колес измеряют нормальный боковой зазор в плоскости, перпендикулярной углу наклона линии зуба. Боковой зазор обычно контролируют при правильном межосевом расстоянии.

Некорригированные зубчатые колеса, обычно работают сопряженными парами на стандартном межосевом расстоянии с утоненными зубьями для обеспечения определенной величины бокового зазора. Боковой зазор должен быть достаточным, чтобы дать возможность зубчатым колесам свободно вращаться без заклинивания зубьев при самых плохих условиях работы (при невыдерживании производственных допусков во время изготовления, неточности сборки, расширении зубьев вследствие увеличения температуры в рабочем агрегате и т. д.). Слишком большой боковой зазор может увеличить уровень шума и уменьшить прочность

На специализирОЕ1анных заводах-изготовителях редукторов направление линии зубьев косозубых цилиндрических колес с целью уменьшения их номенклатуры задают правым, а сопряженных шестерен - - левым; на lie - специализированных заводах направление линии зубьев выбирают таким, чтобы осевые силы, действующие на колеса промежуточных валов, вычитались. [46]

Черновое нарезание зубьев шестерни методом обкатывания можно производить резцовыми головками правого и левого вращения, Более высокая стойкость достигается при нарезании зубьев, с попутной подачей, когда направление вращения резцовой головки противоположно направлению линии зуба . [48]

Шевер и обрабатываемое колесо образуют винтовую пару. Направление линий зубьев желательно иметь различным. Для прямозубых колес обычно применяют правый шевер. [49]

Для направления линии зуба определяющим фактором является положение профиля исходного контура относительно оси колеса во время обработки. [50]

Углы наклона зубьев желательно выбирать такими, чтобы осевые нагрузки на промежуточном валу уравновешивались. При этом направление линии зуба для всех шестерен промежуточного вала должно быть одинаковым. [51]

Червячные фрезы ( рис. 12.21, г) изготовляют с углом профиля 17 5, 20 и 22 5 праворежущими и леворежущими. Обычно направление вращения фрезы выбирают противоположным направлению линии зуба обрабатываемого колеса . Продольная бочкообразность зубьев может быть достигнута вогнутостью наружной поверхности фрезы или изменением наладочных установок станка. [52]

Направление наклона зубьев выбирают так, чтобы осевые усилия были направлены от вершины делительных конусов. Это достижимо, когда на малом колесе передачи направление линии зуба будет совпадать с направлением вращения, если смотреть стороны внутреннего торца. [54]

Дисковые шеверы по ГОСТ 8570 - 80 изготовляют двух типов и трех классов точности: при обработке зубчатых колес с числом зубьев более 40 - шеверы класса АА - для колес 5 - й степени точности; класса А - для колес 6 - й степени точности и класса В - для колес 7 - й степени точности. Шевер каждого размера изготовляют с правым и левым направлениями линии зуба . Дисковый шевер имеет форму закаленного и шлифованного зубчатого колеса с прямыми или косыми зубьями с большим числом стружечных канавок, расположенных на боковой поверхности зубьев. Шеверы типа 1 имеют сквозные стружечные канавки ( табл. 116), а шеверы типа 2 - глухие ( табл. 117), расположенные параллельно торцам, перпендикулярно направлению линии зуба, и канавки трапецеидальной формы. Шеверы с канавками, расположенными параллельно торцам, получили наибольшее применение. [55]

Направление линии зуба выбирают обычно левым для всех косозубых колес первичного и вторичного вала. В этом случае все косозубые зубчатые колеса промежуточного вала имеют правое направление линии зуба . [56]

Обкатные конические и гипоидные передачи, а также шестерни полуобкатных передач с модулем менее 4 мм обычно нарезают двойным двусторонним способом за один цикл обкатки. Одинарный цикл обкатки характеризуется тем, что направление вращения зуборезной головки соответствует направлению линии зуба обрабатываемой шестерни или колеса. Качание люльки производится снизу вверх при нарезании зубьев шестерни или колеса с правым направлением линии зуба и сверху вниз при обработке шестерни или колеса с левым направлением линии зуба. [57]

Косозубые колеса могут быть с правым и левым направлением линии зуба. Два сопряженных косозубых колеса имеют зубья с разным направлением, например одно колесо имеет правое направление линии зуба , другое левое и наоборот. [59]

. Правой называют такую линию, точка на которой движется по часовой стрелке при удалении вдоль зуба, если смотреть на колесо со стороны торца. (В.И.Анурьев, Справочник конструктора машиностроителя, том 2, стр.249, М:"Машиностроение", 1978

Артиллерист - вертолётчик. Дипломированный инженер-механик. Technologist

Добрый день, уважамые форумчане!
Подскажите пожалуйста, как визуально определить направление зуба червячного колеса (правое или левое). Заранее спасибо

Вот пример левого червяка

А ниже пример Правого червячного зацепления

Конструктор, инженер-механик на пенсии

вообще-то меня старики учили так:
Колесо-лежит на торце, зубья наклоняются на право, значит правое(справедливо также и для косозубых колес)
Червяк-режется как винт, по аналогии с винтом, правая резьба, левая резьба

вообще-то меня старики учили так:
Колесо-лежит на торце, зубья наклоняются на право, значит правое(справедливо также и для косозубых колес).

Спасибо всем, разобрался. А поднимал тему потому, что заказал шестерню на редуктор в станок. Чертёж шестерни был в паспорте. Там направление указано - правое. А мне прислали левую шестерню. И пытались доказать, что я не прав и не оттуда смотрю на неё. Вот и поднял тему. Правда всё очень быстро решилось, через день мне уже прислали нормальную шестерню и извинились за ошибку. Ещё раз всем спасибо!

С червеками не сталкивался, но если справедливо и для кососубых колес то проще всего такое правило: ребро какой ладони руки (правой или левой) ложиться естественным образом на линию направления зуба то направление и считать углом наклона.

Колесо-лежит на торце, зубья наклоняются на право, значит правое(справедливо также и для косозубых колес)

ребро какой ладони руки (правой или левой) ложиться естественным образом на линию направления зуба то направление и считать углом наклона.

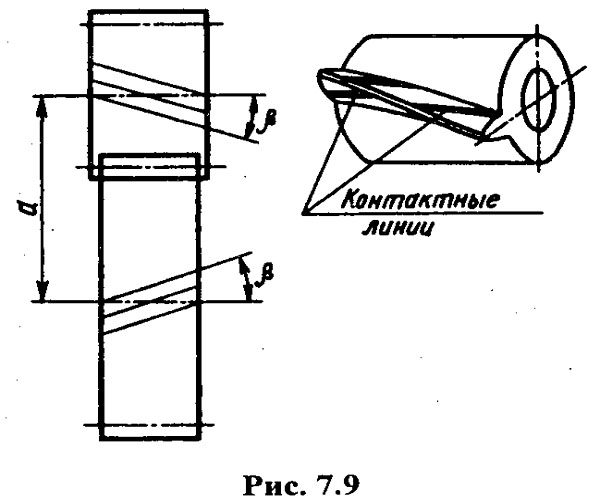
Косозубыми называют колеса, у которых теоретическая делительная линия зуба является частью винтовой линии постоянного шага (теоретической делительной линией называется линия пересечения боковой поверхности зуба с делительной цилиндрической поверхностью). Линия зуба косозубых колес может иметь правое и левое направление винтовой линии. Угол наклона линии зуба обозначается β (рис. 7.9).

Косозубая передача с параллельными осями имеет противоположное направление зубьев ведущего и ведомого колес и относится к категории цилиндрических зубчатых передач, так как начальные поверхности таких зубчатых колес представляют собой боковую поверхность цилиндров.

Передача с косозубыми колесами, оси которых скрещиваются, имеет одинаковое направление зубьев обоих колес и называется винтовой зубчатой передачей (см. Рис. 7.1, и), которая относится к категории гиперболоидных зубчатых передач, так как начальные поверхности таких зубчатых колес являются частями однополостного гиперболоида вращения; Делительные поверхности этих колес — цилиндрические.

Угол перекрытия косозубого колеса состоит из угла торцового и угла осевого перекрытий, следовательно, коэффициент перекрытия ε_γ косозубой передачи равен сумме коэффициентов торцового ε_α и осевого ε_β перекрытия

поэтому у косозубой передачи нет периода однопарного зацепления.

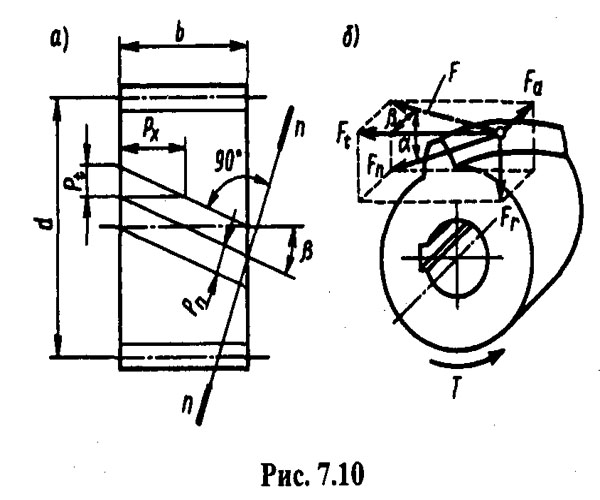
Косозубые колеса обрабатывают теми же зуборезными инструментами, что и прямозубые, поэтому стандартные параметры колес задаются в нормальном к зубу сечении пп (рис. 7.10, а). Нормальный модуль т_п= р_n/π, где р_n — нормальный шаг, измеренный по делительной поверхности. Кроме нормального модуля в косозубых колесах различают: окружной модуль т_t = р_t/π , где р_t — окружной шаг, измеряемый по дуге делительной окружности в торцовом сечении; осевой модуль т_х = р_х/π, где р_х — осевой шаг, измеряемый по образующей делительного цилиндра.

Так как р_t = р_n /cosβ , то т_t = т_п /cosβ.

Размеры зубьев косозубого колеса определяют по нормальному модулю, т. е.

диаметр делительной окружности колеса по окружному модулю

Угол перекрытия косозубого колеса состоит из угла торцового и угла осевого перекрытий, следовательно, коэффициент перекрытия г_у косозубой передачи равен сумме коэффициентов торцового е_а и осевого Ер перекрытия

поэтому у косозубой передачи нет периода однопарного зацепления.

Косозубые колеса обрабатывают теми же зуборезными инструментами, что и прямозубые, поэтому стандартные параметры колес задаются в нормальном к зубу сечении пп (рис. 7.10, а). Нормальный модуль т_п- р„1% , где р„ — нормальный шаг, измеренный по делительной поверхности. Кроме нормального модуля в косозубых колесах различают: окружной модуль т, = р,/п , гдер, — окружной шаг, измеряемый по дуге делительной окружности в торцовом сечении; осевой модуль т_х = р_х/п , гдер_х — осевой шаг, измеряемый по образующей делительного цилиндра.

Так как р, - p,,/cosp , то т, = m,,/cosp.

Размеры зубьев косозубого колеса определяют по нормальному дулю, т. е.

Размеры косозубых колес и межосевое расстояние передачи опреде- по следующим формулам: диаметр вершин зубьев

а = m,(z_y+ z₂)/2 = /k,,(z, + 2₂)/(2cosp). Коэффициент осевого перекрытия косозубой передачи

где Ъ — ширина венца; р_х — осевой шаг.

Нетрудно показать, что если ц — целое число, то суммарная длина контактных линий будет все время оставаться постоянной, что благоприятно для работы передачи, так как нагрузка на зубья в процессе зацепления будет оставаться постоянной, а шум и динамические нагрузки уменьшатся. Суммарная длина контактных линий в этом случае равна

Силу нормального давления F_n в зацеплении косозубых колес можно разложить на три взаимно перпендикулярные составляющие (рис. 7.10, б): окружную силу F,, радиальную силу F_n и осевую силу F_a, равные:

где Т— передаваемый вращающий момент; a — угол зацепления.

Наличие осевой силы — существенный недостаток косозубых передач. Во избежание больших осевых сил в косозубой передаче угол наклона линии зуба ограничивают значениями Р = 8. 20°, несмотря на то, что с увеличением Р увеличивается прочность зубьев, плавность работы передачи, ее нагрузочная способность.

В современных передачах косозубые колеса имеют преимущественное распространение.

В отличие от косозубой в винтовой зубчатой передаче (см. рис. 7.1, м) между зубьями возникает не линейный, а точечный контакт, что значительно увеличивает контактные напряжения и снижает нагрузочную способность передачи. Кроме того, в винтовой зубчатой передаче значительной величины достигает относительное скольжение зубьев, что существенно снижает ее КПД, создает склонность _к заеданию и вызывает быстрый износ зубьев. Учитывая эти недостатки винтовые зубчатые передачи не следует применять в качестве силовых передач.

Обязательное условие для винтовой зубчатой передачи — равенство нормальных модулей. Углы наклона линии зуба ведущего и ведомого колес могут быть различными и угол скрещивания осей может быть не равен 90°.

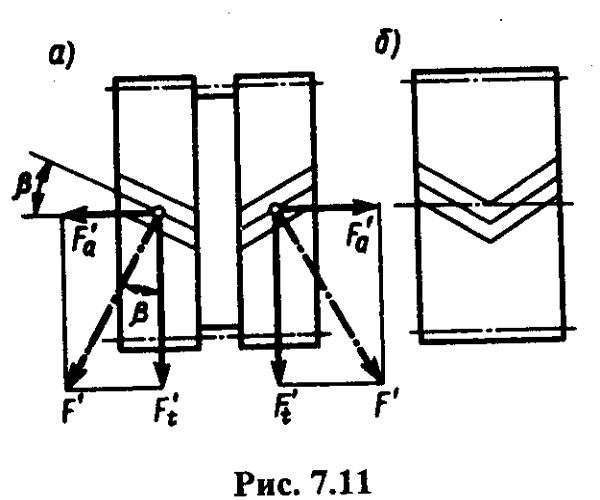
Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями, называется шевронным (см. рис. 7.1, в). Часть венца с зубьями одинакового направления называется полушевроном. Из технологических соображений шевронные колеса изготовляют двух типов (рис. 7.11): с дорожкой посредине колеса (а) и без дорожки (б). В шевронном колесе осевые силы F'_a на полушевронах, направленные в противоположные стороны, взаимно уравновешиваются внутри колеса и на валы и опоры валов не передаются. Поэтому у шевронных колес угол наклона зубьев принимают в пределах β = 25. 40°, в результате чего повышается прочность зубьев, плавность работы передачи и ее нагрузочная способность. Шевронные колеса применяют в мощных быстроходных закрытых передачах. Недостатки ком шевронных колес является высокая трудоемкость и себестоимость изготовления.

Геометрические, кинематические и прочностные расчеты шевронной и косозубой передач аналогичны.

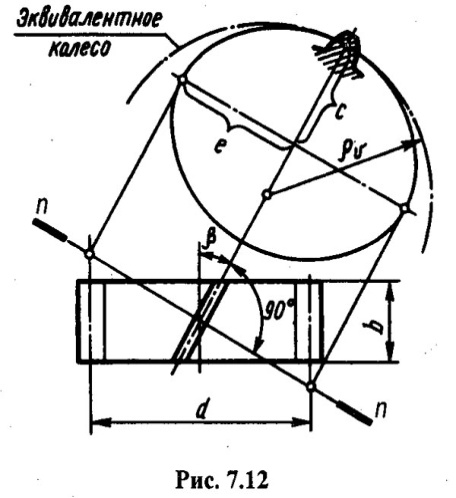
Эквивалентные колеса. Прочность зуба косозубого колеса определяется его формой и размерами в нормальном сечении и длиной зуба. Чтобы унифицировать методику расчетов на прочность прямых и косых зубьев, введено понятие эквивалентного колеса. Эквивалентным прямозубым колесом называется такое колесо, размеры и форма зубьев которого приближенно совпадают с размерами и формой зуба косозубого колеса в нормальном сечении. На рис. 7.12 изображено косозубое колесо, пересеченное плоскостью пп нормальное сечение делительной цилиндрической поверхности этого колеса представляет собой эллипс с полуосями е = d / (2cosβ) и с = d/2 , где d — диаметр делительной окружности. Как известно из аналитической геометрии, максимальный радиус кривизны эллипса

p_υ = е 2 /с = d/(2 cos 2 β).

Этот радиус кривизны придаем за радиус делительного цилиндра эквивалентного колеса, тогда его диаметр

Подставив в это выражение d_υ = m_nz_υ и d =m_nz/ cosβ, получим формулу для определения числа зубьев эквивалентного прямозубого колеса (короче, эквивалентного числа зубьев)

z_υ = z/cos 3 β.

Параметры d_υ и z_υ эквивалентного колеса возрастают с увеличением угла β, что является одной из причин повышения нагрузочной способности косозубых колес по сравнению с прямозубыми и дает возможность при одинаковой нагрузке иметь передачу с меньшими габаритными размерами.

Косозубые зубчатые передачи, как и прямозубые, предназначены для передачи вращательного момента между параллельными валамя (рис. 36). У косозубых колес оси зубьев располагаются не по образующей делительного цилиндра, а по винтовой линии, составляющей с образующей угол (рис. 37). Угол наклона зубьев р принимают равным , он одинаков для обоих колес, но на одном из сопряженных колес зубья наклонены вправо, а на другом влево.

Рис. 36. Цилиндрическая косозубая передача

Достоинства косозубых передач по сравнению с прямозубыми: уменьшение шума при работе; меньшие габаритные размеры; высокая плавность зацепления; большая нагрузочная способность; значительно меньшие дополнительные динамические нагрузки.

За счет наклона зуба в зацеплении косозубой передачи появляется осевая сила.

Направление осевой силы зависит от направления вращения колеса (рис. 37), направления винтовой линии зуба, а также от того, каким является колесо — ведущим или ведомым. Осевая сила дополнительно нагружает валы и опоры, что является недостатком косозубых передач.

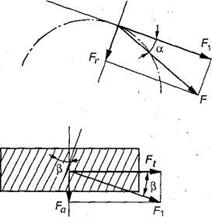
Рис. 37. Усилия в косозубой цилиндрической передаче

Шевронные зубчатые колеса представляют собой разновидность косозубых колес (рис. 38).

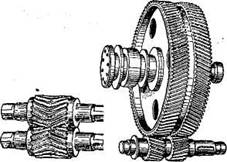
А) б)

Рис. 38. Шевронная зубчатая передача

Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями (рис. 38, а), называют шевронным колесом. Часть венца зубчатого колеса, в пределах которого линии зубьев имеют одно направление, называют полушевроном. Различают шевронные колеса с жестким углом (рис. 38, б), предназначенным для выхода режущего инструмента при нарезании зубьев. Шевронные передачи обладают всеми преимуществами косозубых, а осевые силы (рис. 39) противоположно направлены и на подшипник не передаются.

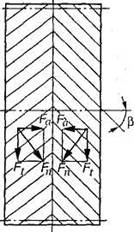
Рис.39. Усилия в зацеплении шевронных зубчатых колес

В этих передачах допускают большой угол наклона зубьев ( ). Ввиду сложности изготовления шевронные передачи применяют реже, чем косозубые, т.е. в тех случаях, когда требуется передавать большую мощность и высокую скорость, а осевые нагрузки нежелательны.

Рис. 40

Косозубые и шевронные колеса в отличие от прямозубых имеют два шага и два модуля: в нормальном сечении (см. рис. 44) по делительной окружности — нормальный шаг р_п, в торцовой плоскости — торцовый шаг р_t. Из условия, что модуль зацепления равен шагу, деленному на число , имеем ; .

Для косозубых и шевронных колес значения нормального модуля т_n стандартизованы, так как профиль косого зуба в нормальном сечении соответствует исходному контуру инструментальной рейки и, следовательно, т = т_п (косозубые и шевронные колеса нарезают, тем же способом и инструментом, что и прямозубые). Нормальный модуль т_п является исходным при геометрических расчетах.

Определим зависимость между нормальным и торцовым шагом и модулем через угол наклона зубьев.

Если левую и правую части разделим на , получим

Геометрические параметры цилиндрической косозубой и шевронной передач с эвольвентным профилем зуба рассчитают по формулам, приведенным в табл. 15. По торцовому модулю т_t рассчитывают делительные (начальные) диаметры, а до т_п — все остальные размеры зубчатых колес.

Таблица 15. Геометрические параметры цилиндрической косозубой передачи

Параметр, обозначение	Расчетные формулы
Нормальный модуль
Торцовый (окружной модуль)
Диаметр вершин зубьев в
Делительный диаметр d
Диаметр впадин зубьев
Шаг нормальный
Шаг торцовый (окружной)
Окружная толщина зубьев
Ширина впадин зубьев
Высота зуба
Высота головки зуба
Высота ножки зуба
Радиальный зазор
Межосевое расстояние
Длина зуба
Ширина венца

Окружная сила . На косой зуб действует осевая сила (см. рис. 37), радиальная (распорная) сила .

В косозубдй передаче сила , действующая на зуб косозубого колеса (см. рис. 44), направлена по нормали к профилю зуба, т.е. по линии зацепления эквивалентного прямозубого колеса, и составляет угол с касательной к
эллипсу.

Эту силу разложим на две составляющие: окружную силу на эквивалентном колесе и радиальную (распорную) силу на этом колесе .

Если, в свою очередь, силу разложить по двум направлениям, то получим такие силы: — окружную силу, — осевую.

Для зубчатого колеса с шевронным зубом окружную силу и распорную определяют по тем же формулам, что и для косозубой передачи т.е. , . В шевронной передаче осевая сила (см. рис. 39).

Винтовая передача (разновидность косозубой) состоит из двух косозубых цилиндрических колес (рис. 41). Однако в отличие от косозубых цилиндрических передач с параллельными валами касания между зубьями здесь происходит в точке и при значительных скоростях скольжения. Поэтому при значительных нагрузках винтовые зубчатые передачи работать удовлетворительно не могут.

Читайте также: