Как найти дельта лямбда в оптике
Оптика - это раздел физики, изучающий природу светового излучения, его распространение и взаимодействие с веществом. Световые волны - это электромагнитные волны. Длина волны световых волн заключена в интервале [0,4·10 -6 м ÷ 0,76·10 -6 м]. Волны такого диапазона воспринимаются человеческим глазом.
Свет распространяется вдоль линий, называемых лучами. В приближении лучевой (или геометрической) оптики пренебрегают конечностью длин волн света, полагая, что λ→0. Геометрическая оптика во многих случаях позволяет достаточно хорошо рассчитать оптическую систему. Простейшей оптической системой является линза.
При изучении интерференции света следует помнить, что интерференция наблюдается только от когерентных источников и что интерференция связана с перераспределением энергии в пространстве. Здесь важно уметь правильно записывать условие максимума и минимума интенсивности света и обратить внимание на такие вопросы, как цвета тонких пленок, полосы равной толщины и равного наклона.
При изучении явления дифракции света необходимо уяснить принцип Гюйгенса-Френеля, метод зон Френеля, понимать, как описать дифракционную картину на одной щели и на дифракционной решетке.
При изучении явления поляризации света нужно понимать, что в основе этого явления лежит поперечность световых волн. Следует обратить внимание на способы получения поляризованного света и на законы Брюстера и Малюса.
Таблица основных формул по оптике
Физические законы, формулы, переменные
Формулы оптики
Абсолютный показатель преломления
где с - скорость света в вакууме, с=3·108 м/с,
v - скорость распространения света в среде.
Относительный показатель преломления
где n2 и n1 - абсолютные показатели преломления второй и первой среды.
Закон преломления
где i - угол падения,
r - угол преломления.
Формула тонкой линзы
где F - фокусное расстояние линзы,
d - расстояние от предмета до линзы,
f - расстояние от линзы до изображения.
Оптическая сила линзы
где R1 и R2 - радиусы кривизны сферических поверхностей линзы.
Для выпуклой поверхности R>0.
Для вогнутой поверхности R

Оптическая длина пути:
где n - показатель преломления среды;
r - геометрическая длина пути световой волны.
Оптическая разность хода:
L1 и L2 - оптические пути двух световых волн.
Условие интерференционного
где λ0 - длина световой волны в вакууме;
m - порядок интерференционного максимума или минимума.
![]()

Оптическая разность хода в тонких пленках
в отраженном свете:
в проходящем свете:
где d - толщина пленки;
i - угол падения света;
n - показатель преломления.

Ширина интерференционных полос в опыте Юнга:
где d - расстояние между когерентными источниками света;
L - расстояние от источника до экрана.
Условие главных максимумов дифракционной решетки:
где d - постоянная дифракционной решетки;
φ - угол дифракции.
![]()
Разрешающая способность дифракционной решетки:
где Δλ - минимальная разность длин волн двух спектральных линий, разрешаемых решеткой;
m - порядок спектра;
N - общее число щелей решетки.
Закон Малюса:
где I0 - интенсивность плоско-поляризованного света, падающего на анализатор;
I - интенсивность света, прошедшего через анализатор;
α - угол между плоскостью поляризации падающего света и главной плоскостью анализатора.
Связь интенсивности естественного света Iест с интенсивностью света, прошедшего поляризатор (и падающего на анализатор):
Дифракционная решетка - оптическое устройство, представляющее собой совокупность большого числа параллельных щелей, равноудаленных друг от друга.
Суммарная ширина щели и штриха (a+b=d) – период решетки.
! d=((a+b)*N)/N=C/N!, где С –ширина решетки, N -число штрихов на ней.

на нем: Л- линза; Р – решетка; Э - экран
Максимумы, которые образуются на экране, после интерференции вторичных волн, идущих от узких щелей, удовлетворяют условию:
!d*sin фи = k*лямбда! - формула дифракционной решетки.
фи - угол дифракции (угол отклонения от прямолинейного направления);
k - порядок спектра;
лямбда - длина волны света, освещающего решетку,
Дифракционные спектры для монохроматического света представляет собой чередование максимумов и минимумов по обе стороны от центрального механизма. Максимумы имеют цвет соответствующей длины света, освещающего решетку.
Если решетку освещать белым светом, то центральный максимум будет белым, а остальные будут представлять собой чередование цветных полос плавно переходящих друг в друга, т. к. sin фи= k*лямбда/d - зависит от длины волны света. D = к/t - угловая дисперсия решетки. R =k*N - разрешающая способность.
Диффузия в жидкости. Уравнение Фика. Уравнение диффузии для мембран.
Диффузия - самопроизвольное проникновение молекул одного вещества между молекулами других.
Явление диффузии - важный элемент диффракционирования мембран. При диффузии происходит перенос массы вещества. В биофизике это называется транспорт частиц. Основным уравнением диффузии является уравнение Фика:

где I – плотность частиц при диффузии в жидкость.

D – коэффициент диффузии.
Коэффициент 1/3 возник ввиду трехмерного пространства и хаоса в движении молекул (в среднем в каждом из 3-х направлений перемещается 1/3 часть всех молекул)
сигма - средняя длина свободного пробега молекул
тау -среднее время оседлой жизни молекул
С- массовая концентрация молекул
Х- перемещение молекул вдоль оси X

- градиент массовой концентрации
Уравнение диффузии можно записать в виде:

n – концентрация молекул.

Градиент концентрации
R- универсальная газовая постоянная; Т- абсолютная температура градиент химического потенциала,

Тогда
С - концентрация частиц. А Эйнштейн показал, что D пропорционально Т. Дня биологических мембран уравнение Фика имеет вид:

- концентрация молекул внутри клеток

- коэффициент проницаемости
l – толщина мембраны.
Дифракция света на щелях.
Дифракцией света называют явление отклонения света от прямолинейного распространения в среде с резкими неоднородностями.
Описать картину дифракции можно с учетом интерференции вторичных волн.

Рассмотрим дифракцию от узкой щели (АВ)
MN – непрозрачная преграда;
АВ=а – ширина щели;
АВ – часть волновой поверхности, каждая точка которой является источником вторичных волн, которые распространяются за щелью по разным направлениям. Линза соберет лучи А, А1 и В в точке О1 экрана.
АD - перпендикуляр к направлению пучка вторичных волн. Разбили ВD на отрезки =лямда/2.
АА1, А1В - зоны Френеля. Вторичные волны, идущие от двух соседних зон Френеля, не гасят друг друга, так как отличаются по фазе на пи. Число зон, укладывающихся в щели, зависит от длины волны лямда и угла альфа.
Если щель АВ разбить при построении на нечетное число зон Френеля, а ВD на нечетное число отрезков, равных лямда/2, то в точке О1 наблюдается максимум интенсивности света. ВD=а*sinα=+-(2k+1)*лямда/2.
Если щель разбить на четное число зон Френеля, то наблюдается минимум освещенности: а*sinα=+-2k*лямда/2=+-k*лямда.
Поэтому на экране получится система светлых (mах) и темных (min) полос симметричных относительно центра (альфа=треугольник - изменение) - наиболее яркой полосы.
Интенсивность остальных максимумов убывает с увеличением к.
3аконы излучения абсолютно чёрного тела (Стефана - Больцмана, Вина). Формула Планка. Использование термографии в диагностике.
Излучение чёрного тела имеет сплошной спектр. Графически это выглядит для разных температур так:
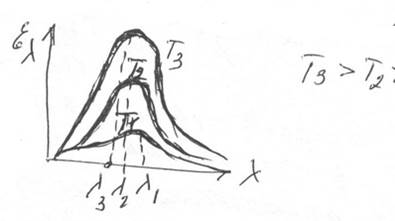
Существует максимум спектральной светимости, который при повышении
температуры смещается в сторону коротких волн.
По мере нагревания чёрного тела его энергетическая светимость (Re)
увеличивается: Re = опред интеграл от 0 до бескон от Eлямда*dлямда
Стефан и Больцман установили, что Re=сигма*T^4
Сигма = 5,6696*10^-8 Вт/K*м^2 - постоянная Стефана-Больцмана,
T=t+273 - абсолютная (термодинамическая) температура по шкале
Кельвина. Все замечали это на практике, чем выше температура спирали, нагретой печи, тем больше они излучают тепла.
Планк получил формулу для спектральной плотности абсолютно черного тела (Eлямда) и серого тела (r лямда) (лямда-индекс): Eлямда=2п*h*c^2/лямда^5 * 1/exp[h*c/k*T*лямда-1]
альфа - коэффициент поглощения
h - постоянная Планка;
С - скорость света в вакууме;
лямда - длина волны;
k - постоянная Больцмана;
Т - абсолютная температура.
2 Затухающие колебания и декремент затухания. Апериодические колебания.
Свободные колебания (происходящие без внешнего воздействия периодически действующей силы) являются затухающими. График затухающих колебаний имеет вид:


Амплитуда колебаний с каждым разом убывает. Затуханию способствуют силы трения и сопротивления, возникающие в средах. Пусть r-коэффициент трения, характеризующий свойство среды оказывать сопротивление движению. Тогда БЕТТА= r/2m – коэффицент затухания.
Wo= корень(K/m) – циклическая частота собственных колебаний, тогда W^2=Wo^2-БЕТТА^2, где W – циклическая частота затухания колебаний.
Быстрота затухания колебаний определяется коэффициентом затухания. Уравнение затухающих колебаний имеет вид А=Ао*l в степени минус бета*t
Ao – первоначальная амплитуда, А-амплитуда затухающих через время t.
Лямда=lnA(t)/A(t+T)=lnAo*(e в степени минус бета*t)/Ao*e^-бета*(t+T)=ln(e^ бета*t) –логарифмический декрет затухания.
!Лямда=бета*Т!- связь логарифмического декремента затухания с коэффициентом затухания. При сильно затухании колебания становятся апериодическими (если бета^2>Wo^2)
№31 Импеданс полной цепи переменного тока. Сдвиг фаз. Резонанс напряжения.
Рассмотрим последовательно соединенные R, L, C.
При последовательном соединении:

1) Uвх=U0*cosW*t=Ur+Ul+Uc – входное напряжение.
2) I=I0*cos(W*t-фи) – сила тока в цепи.
Начертим векторную диаграмму:

Ur0 – совпадает по фазе с силой тока;
Ul0 – опережает на пи/2;
Uc0 – отстает от тока на пи/2.
По теореме Пифагора: (U0)^2=(U0r)^2+(U0l-U0c)^2
Сократив обе части уравнения на (I0)^2 получим выражение для полного сопротивления (Z):
Z=квадратный корень из (R^2+(W*L-1/W*c)^2) – импеданс.
Если сопротивление катушки Xl= W*L равно сопротивлению конденсатора Xc=1/W*c, то полное сопротивление Z=R; по закону Ома Iрез=U0/Z=U0/R (Iрез – резонансный ток) – сила тока резко возрастает – РЕЗОНАНС. При этом Ul=Uc>>U0 – резонанс напряжений. Это возможно, т.к. Ul и Uc сдвинуты по фазе между собой на пи:

При этом на резисторе R выделяется максимальное количество теплоты:
№32 Импенданс тканей организма. Эквивалентная Электрическая схема. Оценка жизнеспособности тканей и органов но частотной зависимости к углу сдвига фаз.
Ткани организма проводят как постоянный так и переменный ток. Биологическая мембрана а значит и весь организм обладает емкостным сопротивлением, т.к. обладают емкостью, т.е. способны
накапливать заряд. При пропускании через живые ткани переменного тока наблюдается отставание напряжения от тока. Омические емкостные свойства биологических тканей можно моделировать используя эквивалентные электрические схемы, при любых частотах зависимость сдвига фаз и импенданса от частоты выполняется для схемы

1/Zв2=1/Rв2+1/корень(R1 в2+1/Wв2*Св2)!, где Z-полное сопротивление данной цепи, с - ёмкость.
При малых частотах: Z=R2 При больших частотах: Zmin=(R1*R2)/(R1+R2).

Графическое изображение зависимости импенданса живой ткани от частоты переменного тока.
Сдвиг фаз между током и напряжением tg фи = R/Xc=RWC (1).

Частотная зависимость сдвига фаз живой ткани. При отмирании ткани натрий-калиевый канал биологических мембран разрушается, цитоплазма
клетки (проводник) соединяется с межклеточной
жидкостью(проводник) и емкостные свойства ткани уменьшаются, а это значит, что и импенданс (Z) и сдвиг фаз (фи) меньше зависят от частоты. Мёртвая ткань обладает лишь омическим сопротивлением (R), и не зависит от частоты. Диагностический метод, основанный на регистрации изменения импенданса тканей и сдвига фаз называется РЕОГРАФИЕЙ.
Интерференция — такое наложение волн, при котором происходит их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от соотношения между фазами этих волн.
Необходимые условия для наблюдения интерференции:
1) Волны должны иметь одинаковые (или близкие) частоты, чтобы картина, получающаяся в результате наложения волн, не менялась во времени;
2) Волны должны быть однонаправленными (или иметь близкое направление); две перпендикулярные волны никогда не дадут интерференции. Волны, для которых выполняются эти два условия, называются когерентными .
При наложении когерентных волн возможны два предельных случая:
1) Условие максимума :
Разность хода волн равна целому числу длин волн (иначе четному числу длин полуволн). \[d_2=d_1=2k\dfrac<\lambda>\] где ( \(k=0, \pm 1,\pm 2, \pm 3. \) ). В этом случае волны в рассматриваемой точке приходят с одинаковыми фазами и усиливают друг друга –– амплитуда колебаний этой точки максимальна и равна удвоенной амплитуде.
2) Условие минимума :
Разность хода волн равна нечетному числу длин полуволн. \[d_2=d_1=(2k+1)\dfrac<\lambda>\] где ( \(k=0, \pm 1,\pm 2, \pm 3. \) ). Волны приходят в рассматриваемую точку в противофазе и гасят друг друга. Амплитуда колебаний данной точки равна нулю.
Каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн.
Дифракция волн — явление отклонения волны от прямолинейного распространения и огибания волной препятствия.
При дифракции происходит искривление поверхности волны у краев препятствия. Особенно явно дифракция проявляется в том случае, если размеры препятствия сравнимы с длинами волн.
Явление дифракции можно объяснить при помощи принципа Гюйгенса, так как любую точку поля волны следует рассматривать как источник вторичных волн, которые распространяются по всем направлениям, в том числе и в область геометрической тени препятствия.
В прозрачной плоской дифракционной решетке (см. рисунок) ширина прозрачного штриха равна \(a\) , ширина непрозрачного промежутка — \(b\) . Величина \(d=a+b=\dfrac\) называется периодом дифракционной решетки, где \(N\) — число штрихов на единицу длины решетки.
Пусть плоская монохроматическая волна падает нормально к плоскости решетки. По принципу Гюйгенса-Френеля каждая щель является источником вторичных волн, способных интерферировать друг с другом. Получившуюся дифракционную картину можно наблюдать в фокальной плоскости линзы, на которую падает дифрагированный пучок.
Допустим, что свет дифрагирует на щелях под углом \(\varphi\) . Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, для данного направления \(\varphi\) будут одинаковыми в пределах всей дифракционной решетки:
В тех направлениях, для которых разность хода равна четному числу полуволн, наблюдается интерференционный максимум. Наоборот, для тех направлений, где разность хода равна нечетному числу полуволн, наблюдается интерференционный минимум. Таким образом, в направлениях, для которых углы \(\varphi\) удовлетворяют условию
наблюдаются главные максимумы дифракционной картины. Эту формулу называют формулой дифракционной решетки. В ней \(m\) называется порядком главного максимума. Между главными максимумами располагается \((N - 2)\) слабых побочных максимумов, но на фоне ярких главных максимумов они практически не видны. При увеличении числа штрихов \(N\) главные максимумы, оставаясь на прежних местах, становятся более резкими.
При наблюдении дифракции в белом свете все главные максимумы, кроме нулевого центрального максимума, окрашены. Это объясняется тем, что, как видно из формулы \[\sin\varphi=\dfrac
Звуковыми волнами в широком смысле называются всякие волны, распространяющиеся в упругой среде. В узком смысле звуком называют звуковые волны в диапазоне частот от 16 Гц до 20 кГц, воспринимаемые человеческим ухом. Ниже этого диапазона лежит область инфразвука, выше — область ультразвука.
К основным характеристикам звука относятся громкость и высота. Громкость звука определяется амплитудой колебаний давления в звуковой волнеиизмеряется в специальных единицах — децибелах (дБ). Чем больше амплитуда колебаний в звуковой волне, тем громче звук.
Скорость звука в разных средах различна: чем более упругой является среда, тем быстрее в ней распространяется звук. В жидкостях скорость звука больше, чем в газах, а в твёрдых телах — больше, чем в жидкостях.

На сколько легче поднимать в воде, чем в воздухе ведро с водой объемом V=10 л., масса ведра 1 кг. (Архимедовой силой, создаваемой воздухом можно прен … ебречь). Какую силу нужно приложить, чтобы поднять его?
№1. Какое количество теплоты выделилось при нагревании масла, объем которого 10 л, если температура изменилась от 30 0С до 60 0С. (Табличные значения: … плотность масла = 900кг/ м3; удельная теплоемкость масла = 1800Дж/ кг*0С ). Ответ дайте в кДж. ПЖ с проверкой едениц измерения
4. На какой глубине в пруду давление в 3 раза больше атмосферного? Плотность поды составляет 1000 кг/м³ (очитать Рo= 100000 Па; g = 9,8 Н/кг)
6. Масса пробкового спасательного круга ранна 10 кг. Опреден лите его подъемную силу в морской воде. Плотность морской по- ды составляет 1030 кг/м³, п … лотность пробки - 240 кг/м³ (считать В g=9,8 Н/кг)
Нижню частину сполучених посудин наповнили ртуттю. У ліве коліно налили гас, а в праве — воду, висота стовпчика якої 16 см. Якої висоти має бути стовп … чик гасу, щоб рівень ртуті в посудинах не змінився? У відповідь занести числове значення в одиницях СІ. *
задано направление линий магнитного поля прямого проводника с током (смотри рисунок). Определи направление тока в проводнике.
1. Определите объём стальной плиты, полностью погруженной в воду, если на неё действует выталкивающая сила 35 Н. 2. Вычислите архимедову силу, действ … ующую на брусок размером 2х10х4 см, если он наполовину погружен в Спирт. 3. Тело объёмом 4 дм имеет массу 4 кг. Утонет ли это тело в бензине? 4. Какой по весу груз сняли с парохода, если осадка его уменьшилась на 20 см? Площадь горизонтального сечения парохода на уровне воды 4000 м2. 5. По реке плывет льдина. Какая её часть погружена в воду, если Плотность льда 0,9г/см3 ? 6". Полый цинковый шар, наружный объем которого 200 см, плавает в воде так, что половина его погружается в воду. Рассчитайте объём полости шара РЕШИТЕ ПОЖАЛУЙСТА. ДАЮ 20 БАЛЛОВ
Рассчитайте мощность насоса ,который за 2 минуты перекачивает 1200литров водоы на высоту 10 м.(ро воды =10куб кг/м3,g=10 Н/кг)
Читайте также:

