Что такое дельта лямбда

Обновлено: 09.01.2025

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, ~~только хардкор~~. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Термы:

переменная:	x
лямбда-абстракция (анонимная функция):	λx.t , где x — аргумент функции, t — её тело.
применение функции (аппликация):	f x , где f — функция, x — подставляемое в неё значение аргумента

Применение функции левоассоциативно. Т.е. s t u — это тоже самое, что (s t) u
Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е. λx. λy. x y x означает то же самое, что λx. (λy. ((x y) x))
Скобки явно указывают группировку действий.

Процесс вычисления

Рассмотрим следующий терм-применение:

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

который для простоты можно переписать как

(напомним, что id — это функция тождества вида λx.x )

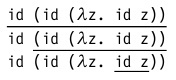
В этом терме содержится три редекса:

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y . Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y , а z — первоначальный терм имел бы вид (λx.λz.x)y и после редукции выглядел бы как λz.y . Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.

Так же бывает, что у нас есть абстракция λx.t x , причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t . Такое преобразование называется η-конверсией.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Леди Лямбдадельта - персонаж из визуальной новеллы, аниме и манги Umineko no Naku Koro ni. Могущественная ведьма, сенатор и странница по историям, Лямбдадельта была одним из ключевых персонажей, представая как в качестве героя, так и в качестве злодея.

Содержание

Внешность

Лямбдадельта появляется в облике маленькой девочки (визуально 12-15 лет), несмотря на то, что ей более 1000 лет. У неё короткие светлые волосы и янтарные глаза. Вся одежда розовая (беретка, платье, полосатые чулки, туфли), покрытая множеством бантиков. Единственными исключение из этого являются ее длинные черные перчатки, а также некий аксессуар в виде тыквы.

Иногда Лямбдадельта превращается в конфеты. Впрочем даже её человеческое тело изнутри состоит из сладкой ваты и не содержит крови или органов.

Её часто можно увидеть, жующую попкорн из коробки, во время наблюдения за чем-то интересным.

Личность

При первом же появлении Лямбдадельта ярко демонстрирует свою детскую личность. Она жизнерадостна и гиперактивна, постоянно отпускает глупые шутки и остро реагирует на всё, что не соответствует её планам.

Более абстрактная форма

Тем не менее, вскоре мы видим темную сторону личности ведьмы Абсолюта. Даже по меркам высших существ, для которых люди - не более, чем фигуры на шахматной доске, Лямбдадельту можно назвать по-настоящему жестокой. Ей не составило никакого труда довести Беатриче до состояния запуганной девочки. Гнев Баттлера после того, как его сестру заживо расчленили на мелкие кусочки раскалёнными клещами, и пригрозили её печальной судьбой в бесконечном количестве параллельных миров, Лямбдадельта охарактеризовала прекрасным лекарством от скуки, но всё же не более, чем лёгкой закуской.

Даже любовь у ведьмы Абсолюта очень своеобразная. Мало того, что она любит другую девушку, так ещё и желает выковырять ей глаза, дабы она не смотрела ни на кого, кроме самой Лямбдадельты. Или же можно превратить объект вожделения в конфету и съесть, чтобы навечно остаться вместе.

В стороне от темной и детской стороны, Лямбда демонстрирует также зрелую. Она может быть спокойной, серьёзной и рассудительной, не реагировать на провокации и давать полезные советы.

Несмотря на такой сложный характер, у ведьмы Абсолюта есть поистине огромное количество друзей, которые искренне любят и уважают её. И ведь есть за что, Лямбдадельта готова ринуться в бой за своих друзей даже тогда, когда пред ней стоит противник, в сравнении с которым сама Лямбдадельта - не более, чем фигура на доске.

Лямбда уважает тех, кто добивается своей цели упорным трудом, не отступая перед любыми трудностями. Иногда она снисходит до обычных людей, чтобы предложить им исполнить одно желание, однако, заинтересовать её может лишь что-то выходящее за рамки человеческого общества (богатства и любви вы от неё не получите, но вот создать вселенную или предоставить статус бога она может).

Известно, что кошмарное прошлое Лямбдадельты оставило глубочайший след на её психике.

"Знаешь. временами этот ужас возвращается ко мне. Интересно. правда ли я сбежала из того ада. Что если. давным-давно я фактически сошла с ума и все ещё там. просто вижу иллюзию всех нас, счастливо болтающих вот так. Этот кошмар до сих пор пугает меня. И поэтому я должна постоянно чувствовать. по-настоящему чувствовать, что это не сон. Эй. вы правда. реальны? Вы ведь не просто мой безумный бред в том аду. Правда? Правда. "

Роль в истории

Лямбдадельта была той, кто даровала магические силы Беатриче, главному злодею первой части новеллы. Также она когда-то проиграла Бернкастель титул сильнейшей ведьмы.

Во время своего первого фактического появления в сюжете, Лямбдадельта оказывает помощь главному герою Баттлеру, давая ему некоторые подсказки. В следующий раз она помогает уже Беатриче. На самом деле, единственной целью ведьмы Абсолюта является создание ситуации, в которой игра затянется навечно, ведь тогда и Бернкастель, ведьма Чудес и объект любовного интереса Лямбдадельты, заинтересовавшаяся игрой, навечно останется там. Беатриче не оправдывает надежд, чем навлекает на себя гнев покровительницы.

После всех основных событий, Бернкастель лично зашивала оторванные конечности Лямбды. Затем представители этой любящей пары решили отправится в очередное путешествие по историям в разные стороны, чтобы когда-нибудь снова встретиться, спустя много-много лет.

Силы и способности

Лямбдадельта - духовная, метафизическая, абстрактная и концептуальная сущность из высшего мира, в котором трехмерные вселенные мира человеческого, могут быть визуализированны в виде крошечных кристаллических Осколков. Для высших существ не имеют значения Физические законы и концепции реального мира, такие как масса, время, расстояние, судьба и смерть.

Понятие, воплощаемое Лямбдадельтой - это получение вознаграждение за тяжелый труд. Один из законов мира гласит, что чем сильнее воля, тем больше шансов добиться желаемого. И это основная суть концепции Лямбды, которая повсюду уважаема людьми, что обеспечивает ей безмерное могущество.

Магия Абсолюта позволяет Лямбдадельте контролировать любые физические и метафизические вероятности в диапазоне от 0 до значений, стремящегося к 100%. Это значит, что она может воплотить любое событие с близкой к абсолюту вероятностью. Не являются исключением даже совсем иррациональные возможности, как например, уничтожение бесконечной сущности, в которой нет ничего, кроме нуля.

То что она может казаться дружелюбной - это ещё не повод фамильярничать, забывая с кем говоришь

При прямых боевых столкновениях с персонажами своего уровня, Лямбдадельта атакует конфетами, попкорном, а также черными дырами, Большими взрывами и Большими сжатиями.

Будучи Вояджером, высокопоставленной ведьмой, стоящей на шаг ниже всемогущего Творца, Лямбдадельта способна свободно перемещаться в пространстве, времени и небытии вне их, путешествуя по разным историям, пересекая вселенные и мультивселенные, миры и измерения.

Будучи Сенатором, Лямбдадельта имеет право войти в священный Город Книг, где хранятся бесчисленные миры историй. Также она может приказывать инквизиторам Великого Небесного Суда.

Лямбдадельта способна предоставить кому угодно достаточно могущества, чтобы он мог стать богоподобным существом, контролирующим своё собственное измерение в высшем мире, в рамках которого может располагаться бесконечная мультивселенная из обычных трехмерных миров.

Кроме всего этого, Лямбдадельта чрезвычайно умна, хитра и расчетлива по меркам людей. Ей не составляет труда сплести детективную историю, решение загадки которой должно проводиться с учетом бесконечных возможностей развития событий, существующих одновременно. Также Лямбдадельта превосходный провокатор, способный просчитать, запугать или вывести из себя практически кого угодно.

Слабостью является то, что как и все ведьмы, Лямбдадельта подвержена скуке. Хотя физическая смерть и даже стирание из существования (без вмешательства высших сил), ничего не значат для неё, ежели Лямбдадельта лишится интереса к жизни, она "умрет", и чем дольше пробудет в таком состоянии, тем меньше будет шансов "воскреснуть", появится риск полного растворения в забвении.

Лямбда-выражения являются одним из наиболее мощных дополнений в C++11 и продолжают развиваться с каждым новым стандартом языка. В этой статье мы пройдемся по их истории и посмотрим на эволюцию этой важной части современного C++.

Вторая часть доступна по ссылке:
Lambdas: From C++11 to C++20, Part 2

Вступление

Я решил взять код у Томаса (с его разрешения!), описать его и создать отдельную статью.

Мы начнем с изучения C++03 и с необходимости в компактных локальных функциональных выражениях. Затем мы перейдем к C++11 и C++14. Во второй части серии мы увидим изменения в C++17 и даже взглянем на то, что произойдет в C++ 20.

С самого начала STL std::algorithms , такие как std::sort , могли принимать любой вызываемый объект и вызывать его для элементов контейнера. Однако в C++03 это предполагало только указатели на функции и функторы.

Но проблема заключалась в том, что вы должны были написать отдельную функцию или функтор в другой области видимости, а не в области видимости вызова алгоритма.

В качестве потенциального решения вы могли бы подумать о написании локального класса функторов — поскольку C++ всегда поддерживает этот синтаксис. Но это не работает…

Посмотрите на этот код:

Попробуйте скомпилировать его с -std=c++98 , и вы увидите следующую ошибку в GCC:

Если мы посмотрим на N3337 — окончательный вариант C++11, то увидим отдельный раздел для лямбд: [expr.prim.lambda].

Далее к C++11

Вот базовый пример кода, который также показывает соответствующий объект локального функтора:

Вы также можете проверить CppInsights, который показывает, как компилятор расширяет код:

Посмотрите на этот пример:

В этом примере компилятор преобразует:

Во что-то похожее на это (упрощенная форма):

Некоторые определения, прежде чем мы начнем:

Вычисление лямбда-выражения приводит к временному prvalue. Этот временный объект называется объектом-замыканием (closure object).

Тип лямбда-выражения (который также является типом объекта-замыкания) является уникальным безымянным non-union типом класса, который называется типом замыкания (closure type).

Несколько примеров лямбда-выражений:

Поскольку компилятор генерирует уникальное имя для каждой лямбды, узнать его заранее не представляется возможным.

Более того [expr.prim.lambda]:
Тип замыкания, связанный с лямбда-выражением, имеет удаленный ([dcl.fct.def.delete]) конструктор по умолчанию и удаленный оператор присваивания.

Поэтому вы не можете написать:

Это приведет к следующей ошибке в GCC:

Оператор вызова

По умолчанию это встроенный константный метод. Вы можете изменить его, указав mutable после объявления параметров:

Захватив переменную, вы создаете член-копию этой переменной в типе замыкания. Затем внутри тела лямбды вы можете получить к нему доступ.

[&] — захват по ссылке, все переменные в автоматическом хранилище объявлены в области охвата
[=] — захват по значению, значение копируется
[x, & y] — явно захватывает x по значению, а y по ссылке

Вы можете поиграться с полным примером здесь: @Wandbox

Хотя указание [=] или [&] может быть удобно — поскольку оно захватывает все переменные в автоматическом хранилище, более очевидно захватывать переменные явно. Таким образом, компилятор может предупредить вас о нежелательных эффектах (см., например, примечания о глобальных и статических переменных)

И важная цитата:

По умолчанию operator() типа замыкания является константным, и вы не можете изменять захваченные переменные внутри тела лямбда-выражения.
Если вы хотите изменить это поведение, вам нужно добавить ключевое слово mutable после списка параметров:

В приведенном выше примере мы можем изменить значения x и y… но это только копии x и y из прилагаемой области видимости.

Захват глобальных переменных

Если у вас есть глобальное значение, а затем вы используете [=] в лямбде, вы можете подумать, что глобальное значение также захвачено по значению… но это не так.

Поиграть с кодом можно здесь: @Wandbox

Захватываются только переменные в автоматическом хранилище. GCC может даже выдать следующее предупреждение:

Это предупреждение появится только в том случае, если вы явно захватите глобальную переменную, поэтому, если вы используете [=] , компилятор вам не поможет.
Компилятор Clang более полезен, так как генерирует ошибку:

Захват статических переменных

Захват статических переменных аналогичен захвату глобальных:

Поиграть с кодом можно здесь: @Wandbox

И снова, предупреждение появится, только если вы явно захватите статическую переменную, поэтому, если вы используете [=] , компилятор вам не поможет.

Захват члена класса

Знаете ли вы, что произойдет после выполнения следующего кода:

Код объявляет объект Baz, а затем вызывает foo() . Обратите внимание, что foo() возвращает лямбду (хранящуюся в std::function ), которая захватывает член класса.

Поскольку мы используем временные объекты, мы не можем быть уверены, что произойдет, при вызове f1 и f2. Это проблема висячих ссылок, которая порождает неопределенное поведение.

Опять же, если вы укажете захват явно ([s]):

Компилятор предотвратит вашу ошибку:

Move-able-only объекты

Если у вас есть объект, который может быть только перемещен (например, unique_ptr), то вы не можете поместить его в лямбду в качестве захваченной переменной. Захват по значению не работает, поэтому вы можете захватывать только по ссылке… однако это не передаст его вам во владение, и, вероятно, это не то, что вы хотели.

Сохранение констант

Если вы захватываете константную переменную, то константность сохраняется:

Возвращаемый тип

В C++11 вы можете пропустить trailing возвращаемый тип лямбды, и тогда компилятор выведет его за вас.

Первоначально вывод возвращаемого типа значения был ограничен лямбдами, содержащими один оператор return, но это ограничение было быстро снято, поскольку не было проблем с реализацией более удобной версии.

Таким образом, начиная с C++11, компилятор может вывести тип возвращаемого значения, если все операторы return могут быть преобразованы в один и тот же тип.

Если все операторы return возвращают выражение и типы возвращаемых выражений после преобразования lvalue-to-rvalue (7.1 [conv.lval]), array-to-pointer (7.2 [conv.array]) и function-to-pointer (7.3 [conv.func]) такое же, как у общего типа;

Поиграться с кодом можно здесь: @Wandbox

В вышеприведенной лямбде есть два оператора return , но все они указывают на double , поэтому компилятор может вывести тип.

IIFE — Немедленно вызываемые выражения (Immediately Invoked Function Expression)

В наших примерах я определял лямбду, а затем вызвал ее, используя объект замыкания… но ее также можно вызывать немедленно:

Такое выражение может быть полезно при сложной инициализации константных объектов.

Преобразование в указатель на функцию

Тип замыкания для лямбда-выражения без захвата имеет открытую невиртуальную неявную функцию преобразования константы в указатель на функцию, имеющую тот же параметр и возвращаемые типы, что и оператор вызова функции типа замыкания. Значение, возвращаемое этой функцией преобразования, должно быть адресом функции, которая при вызове имеет тот же эффект, что и вызов оператора функции типа сходного с типом замыкания.

Другими словами, вы можете преобразовывать лямбды без захватов в указатель на функцию.

Поиграться с кодом можно здесь: @Wandbox

Улучшения в C++14

C++14 добавил два значительных улучшения в лямбда-выражения:

Захваты с инициализатором
Общие лямбды

Возвращаемый тип

Вывод типа возвращаемого значения лямбда-выражения был обновлен, чтобы соответствовать правилам автоматического вывода для функций.

Возвращаемый тип лямбды — auto, который заменяется trailing возвращаемым типом, если он предоставляется и/или выводится из операторов возврата, как описано в [dcl.spec.auto].

Захваты с инициализатором

Короче говоря, мы можем создать новую переменную-член типа замыкания и затем использовать ее внутри лямбда-выражения.

Это может решить несколько проблем, например, с типами, доступными только для перемещения.

Перемещение

Теперь мы можем переместить объект в член типа замыкания:

Оптимизация

Другая идея состоит в том, чтобы использовать его как потенциальную технику оптимизации. Вместо того, чтобы вычислять какое-то значение каждый раз, когда мы вызываем лямбду, мы можем вычислить его один раз в инициализаторе:

Захват переменной-члена

Инициализатор также можно использовать для захвата переменной-члена. Затем мы можем получить копию переменной-члена и не беспокоиться о висячих ссылках.

Поиграться с кодом можно здесь: @Wandbox

В foo() мы захватываем переменную-член, копируя ее в тип замыкания. Кроме того, мы используем auto для вывода всего метода (ранее, в C++11 мы могли использовать std::function ).

Обобщенные лямбда-выражения

Еще одно существенное улучшение — это обобщенная лямбда.
Начиная с C++14 можно написать:

Это эквивалентно использованию объявления шаблона в операторе вызова типа замыкания:

Такая обобщенная лямбда может быть очень полезна, когда трудно вывести тип.

В этой статье мы начали с первых дней лямбда-выражений в C++03 и C++11 и перешли к улучшенной версии в C++14.

Вы увидели, как создавать лямбду, какова основная структура этого выражения, что такое список захвата и многое другое.

В следующей части статьи мы перейдем к C++17 и познакомимся с будущими фичами C++20.

Вторая часть доступна здесь:

В очередном опусе Итана Сигеля резанула фраза

Пронаблюдав за удалёнными сверхновыми и измерив, как Вселенная расширялась миллиарды лет, астрономы обнаружили нечто удивительное, загадочное и неожиданное.

By observing distant supernovae and measuring how the Universe had expanded over billions of years, astronomers discovered something remarkable, puzzling and entirely unexpected

О какой неожиданности может идти речь? Там ведь совершенно шикарная история длиной в 80 лет с яркими открытиями и закрытиями. История про то, как на самом деле делается настоящая наука. История скорее про физиков, чем про физику.

О чём вообще весь сыр-бор?

Первую версию Общей Теории Относительности (ОТО) Альберт Эйнштейн представил публике 25 ноября 1915 года. В оригинале уравнения ОТО Эйнштейна выглядели вот так:

или, в современной записи, вот так:

Для неумеющего в тензоры читателя понятнее уравнение (1) в оригинальной записи Эйнштейна. Там написано, что энергия-импульс материи G равен кривизне пространства R плюс тензор Риччи S. (Этот самый тензор Риччи тоже есть кривизна, только в более другой форме).
Сейчас, решая уравнение ОТО, энергию-импульс обычно считают известным, а ищут как раз кривизну. Поэтому в современной записи стороны уравнения поменяли местами. Заодно поменяли буковки: G → T, S → R_μν.

Откуда есть пошла лямбда

Но физика — это вам не математика. Здесь нельзя взять формулу и напихать в неё добавочных слагаемых просто так. Нужно иметь очень веские основания, и теоретические, и экспериментальные.

Хотя ниже вы увидите, насколько мало Эйнштейн знал о Вселенной в те годы, но тогда, в 1916, такие основания у него были. Альберт Германович точно знал, что звёзды не попадали друг на друга и совершенно не собираются этого делать в обозримом будущем. Однако, в ОТО-1915 было только притяжение, которое нужно было чем-то сбалансировать.

Первое физическое толкование смысла лямбды

В такой трактовке ненулевое значение Λ означает, что наша Вселенная искривлена сама по себе, в том числе и при отсутствии какой-либо гравитации. Ну, вот такой нам достался мир. Однако, большинство физиков в это не верят, и считают, что у наблюдаемого искривления должна быть какая-то внутренняя причина. Какая-то неведомая доселе фигня, которую можно открыть.

На сегодняшний день измеренная кривизна пространства Вселенной таки равна нулю, но с очень паршивой точностью, порядка 0.4%. И не очень-то видно способов эту точность улучшить.
С измерениями кривизны есть две концептуальные проблемы.

Первая в том, что мы не можем измерить совсем пустое пространство, потому что просто ничего там не видим. А если там есть что-то, что мы таки видим, то пространство уже не пустое и, значит, уже дополнительно искривлено гравитацией.

Допустим, у нас есть как-то измеренные координаты объектов, плюс пачка фотографий этих объектов в разных ракурсах (снятых из разных точек). Тогда мы можем вычислить кривизну пространства. Например, гравитация Солнца отклоняет пролетающий мимо свет далёких звёзд. Во время солнечных затмений это отклонение можно измерить экспериментально и сравнить с предсказаниями ОТО.

Теперь наоборот: допустим, мы знаем кривизну пространства, и у нас есть пачка фотографий. Тогда, если кривизна достаточно хорошая, без чёрных дыр и т.п. — мы можем вычислить координаты объектов на фото. Именно так работают наши глаза, точнее мозги, когда вычисляют расстояние до объектов по двум фоткам с разных точек.

Поэтому измерить кривизну наблюдаемой Вселенной в целом мы можем только из очень окольных соображений.

Вселенная Фридмана

Meanwhile in Russia, не смотря на войны и революции, над теорией ОТО бился прапорщик (и по совместительству профессор) Александр Александрович Фридман. Он рассмотрел все варианты лямбд и выяснил следующее:

При Λ < 0 имеют место лишь силы притяжения, как гравитационные, так и вызванные кривизной ~~впуклого~~вогнутого пространства. Рано или поздно звёзды и галактики в таком мире таки попадают друг на друга. Причём конец будет неожиданно быстрым и очень горячим.

Но самое интересное происходит при Λ = 0. Здесь всё зависит от начальных условий — т.е. координат и скоростей конкретных галактик. Возможны три варианта: большое сжатие, большой разлёт и стационарный вариант, когда галактики разлетаются, но с относительно небольшими скоростями и без ускорения.

Сегодня вышеописанные ситуации называются космологическими решениями Фридмана.

Статьи Фридмана 1922 и 1924 годов отменяли необходимость в лямбда-члене, из-за чего поначалу были приняты Эйнштейном в штыки.

За свою работу Фридман вполне мог претендовать на Нобелевку.

Летом 1925 он женился, поехал в свадебное путешествие в Крым, съел там немытую грушу, заразился тифом и в сентябре — умер.

И да, статья Итана про примерно такой график (конкретно на этом учтены данные на 2010 год):

Здесь по горизонтали отложено z — это красное смещение, по вертикали наблюдаемая яркость сверхновых особого типа Ia, которые всегда выделяют одно и то же количество энергии. Вообще, это два способа измерения одного и того же расстояния, но, так сказать, в разные моменты времени.

Серые палки — наблюдавшиеся события с их погрешностью измерений. Синим пунктиром отложено предсказание при Λ = 0, красной линией — аппроксимация фактически наблюдаемых значений. Отклонение красной линии от прямой означает, что Вселенная расширяется ускоренно. Но Эйнштейн об этом так и не узнал.

Вселенная Каптейна

Перейдём к экспериментальной части.

Голландский астроном Якобус Корнелиус Каптейн открыл звезду Каптейна в 1897, после чего приступил к opus magnum всей своей жизни. Объединяя огромное количество наблюдений разных обсерваторий, он попытался создать первую карту Вселенной. По его карте выходило, что вселенная имеет форму вращающегося (sic!) диска крышесносящего по тем временам размера 40000 световых лет, причём Солнце находится отнюдь не в центре, а вполне себе на задворках. Закончена и опубликована эта работа была только в 1922.

Для понимания уровня тогдашних знаний: то, что Каптейн считал невероятно огромной Вселенной, сегодня считается совершенно рядовой, ничем не примечательной среди миллиардов таких же… галактикой Млечный Путь. Тем не менее, заслуга Каптейна в том, что он открыл её вращение и приблизительно вычислил её центр.

Наблюдения Хаббла (астронома, а не телескопа)

Статью со своими открытиями, из которой следовало, что Вселенная значительно больше, чем наш Млечный путь, Хаббл представил американскому астрономическому обществу первого января 1925. За что и был освистан ~~страдающими от похмелья~~ коллегами, едва свыкшимися с расстояниями Каптейна.

Хаббл не унимался и прикрутил к телескопу ещё и спектрометр. Анализируя красное смещение галактик, он выяснил, что галактики разбегаются, а Вселенная, соответственно, расширяется. Заодно он открыл закон имени себя с константой имени себя (впрочем, закон был предсказан Леметром), и описал всё это в статьях к концу 20-ых годов. Согласно его наблюдениям, оказалась верна модель Фридмана для Λ = 0.

Это выбило из-под лямбды теперь уже и экспериментальные основания её существования.

Здесь ещё нужно упомянуть, что первоначальные оценки Хаббла были очень уж неточными и показывали возраст Вселенной порядка 2 миллиардов лет. Позднее это войдёт в противоречие с данными геофизиков, которые при помощи радиоизотопного анализа оценят возраст Земли в несколько миллиардов лет, и десятилетиями будет сильнейшей головной болью для физиков-космологов.

Стационарная Вселенная Хойла

С начала 30-ых годов вопрос с лямбдой считался решённым, и из мейнстримных физиков ей никто толком не занимался. Одним из редких исключений, рискнувших попереть супротив самого Эйнштейна, стал британец Фред Хойл.

Речь пойдёт о гелии. Этот элемент феноменально инертен и не хочет ни с чем реагировать. Причём не только химически, но и физически тоже, если мы говорим про гелий-4. Его ядро — альфа частица — имеет пиковую энергию связи на нуклон в своей области. см. рис из какого-то реферата:

Это значит, что альфа-частица не может присоединить дополнительные протоны или другую альфа-частицу иначе как случайно: это просто-напросто энергетически невыгодно. А в ядрах звёзд ничего кроме протонов и альфа-частиц и нет.

Возникал резонный вопрос: а откуда, собственно, взялись химические элементы тяжелее гелия?

Ближайшее ядро, в которое может превращаться гелий-4, это углерод-12. Но для этого нужно объединить три альфа-частицы.

Проблема в том, что вероятность столкновения трёх альфа-частиц одновременно слишком мала. А двухшаговый процесс (сначала сталкиваются две частицы, потом очень быстро, пока они не разлетелись обратно на две альфа-частицы, в них врезается ещё одна), в принципе, возможен, но расчёты Эдвина Солпитера показывали, что такой процесс идёт слишком вяло, чтобы производить существенные количества углерода.

Однако, по расчётам Хойла выходило, что при наличии такого уровня в три-альфа процессе наступает резонанс, и звёзды — красные гиганты производят достаточно много углерода для нашего существования.

Удивительно, но американцы решили провести небольшой эксперимент на своём ускорителе. И да — триумфально нашли нужный энергетический уровень на 7.65 МэВ, который физики-ядерщики всего мира почему-то проглядели во всех предыдущих экспериментах.

Сегодня такое возбуждённое состояние углерода-12, когда три альфа-частицы фактически выстраиваются по линии, называется хойловским. Соответствующая статья Хойла, Фаулера и супругов-астрономов Джефри и Маргерит Бёрбиджей является краеугольным камнем современных теорий звёздного нуклеосинтеза и настолько часто цитируется, что обозначается просто B²FH, без ссылок и расшифровок.

И — да, на сегодня это чуть ли не единственное известное успешное предсказание на основе антропного принципа.

Однако, из квантовых флуктуаций постоянно рождается новое вещество, причём так, что средняя плотность материи остаётся одинаковой. Расчёты показывают, что в одном кубическом километре пространства должен рождаться всего-навсего один протон раз в 300000 лет (а так же один электрон или что-то типа того для сохранения электрического заряда). Прекрасное число, чтобы исключить любую возможность какой-либо экспериментальной проверки!

Теория стационарной Вселенной серьёзно рассматривалась как альтернатива теории Большого Взрыва в 50-х и начале 60-х. Но экспериментальное открытие в 1964 году предсказанного ТББ реликтового излучения поставило на ней крест.

За статью B²FH дали Нобелевку. Но только Фаулеру, который распорядился провести десятидневный эксперимент. Ни супругам Бёрбиджам, проводившим длительные астрономические наблюдения и собственно написавшим статью, ни автору идеи Хойлу нобелевку не дали — за упорствование в космологической ереси.

Квантовая лямбда

Вернёмся к уравнению ОТО.

Слева (в современной записи) стоит кривизна пространства, сиречь гравитация по ОТО. Справа — тензор энергии-импульса. Под этим тензором стоит жутко сложный матан, но суть в следующем: там учтена вся-вся-вся материя Вселенной во всех видах и состояниях. И обычное вещество, и всякие хитрые частицы, и все виды излучений (кроме гравитации, которая слева).

Теперь мысленно перенесём лямбду вправо. В такой записи это будет не дополнительная кривизна, а какая-то неучтённая энергия (замечу, отрицательная, раз уж мы считаем лямбду положительной). И здесь просматриваются две возможности.

Первая гипотеза состоит в том, что лямбда — это энергия собственно вакуума. Звучит диковато, но на самом деле вполне согласуется с квантовой механикой. Возьмём кусок пространства и уберём из него всё, что хотя бы в принципе можно убрать. Уберём всё вещество, все частицы и все волны, независимо от их природы. Останутся только физические поля в невозмущённом состоянии. Полный штиль.

Так вот, у некоторых полей (например, Хиггсовских) в пустоте ненулевое значение. И теоретически у них есть некоторая энергия. Кроме того, в силу принципа неопределённости у любых полей есть квантовые флуктуации — и они тоже имеют некоторую энергию.

Вместо заключения

Содержание

Внешность

Её часто можно увидеть, жующую попкорн из коробки, во время наблюдения за чем-то интересным.

Личность

Более абстрактная форма

Известно, что кошмарное прошлое Лямбдадельты оставило глубочайший след на её психике.

Роль в истории

Силы и способности

То что она может казаться дружелюбной - это ещё не повод фамильярничать, забывая с кем говоришь

Читайте также: