В идеальном тепловом двигателе увеличилась работа совершаемая газом за один цикл при неизменном
Температуру холодильника тепловой машины Карно понизили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл?
Для каждой величины определите соответствующий характер её изменения:
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
КПД тепловой машины Карно вычисляется по формуле: где — соответственно температуры холодильника и нагревателя, — соответственно теплоты, передаваемые холодильнику и отнимаемые от нагревателя. Работа газа в таком процессе: При понижении температуры холодильника увеличивается КПД тепловой машины, а вместе с ней, при неизменном количестве теплоты, получаемой газом от нагревателя, увеличивается и работа газа.
Температуру нагревателя тепловой машины Карно понизили, оставив температуру холодильника прежней. Количество теплоты, отданное газом холодильнику за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл?
Для каждой величины определите соответствующий характер её изменения:
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
КПД тепловой машины Карно вычисляется по формуле: где — соответственно температуры холодильника и нагревателя, — соответственно теплоты, передаваемые холодильнику и отнимаемые от нагревателя. Работа газа в таком процессе: При понижении температуры нагревателя уменьшается КПД тепловой машины, а вместе с ней, при неизменном количестве теплоты, отданном газом холодильнику, уменьшается и работа газа.
Температуру нагревателя тепловой машины Карно повысили, оставив температуру холодильника прежней. Количество теплоты, отданное газом холодильнику за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл?
Для каждой величины определите соответствующий характер её изменения:
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
КПД тепловой машины Карно вычисляется по формуле: где — соответственно температуры холодильника и нагревателя, — соответственно теплоты, передаваемые холодильнику и отнимаемые от нагревателя. Работа газа в таком процессе: При повышении температуры нагревателя увеличивается КПД тепловой машины, а вместе с ней, при неизменном количестве теплоты, отданном газом холодильнику, увеличивается и работа газа.
Рассмотрим две идеальные тепловые машины. Температуры нагревателя и холодильника первой машины отличаются в 4 раза. Температура холодильника первой тепловой машины равна температуре нагревателя второй тепловой машины. Температура холодильника второй тепловой машины в 6 раз меньше температуры нагревателя первой тепловой машины. Во сколько раз КПД первой машины больше КПД второй машины? Ответ округлите до сотых долей.
По условию для первой тепловой машины
Для второй тепловой машины
Аналоги к заданию № 24098: 24151 Все
Идеальная тепловая машина обменивается теплотой с тёплым телом — окружающей средой, находящейся при температуре +25 °С, и холодным телом с температурой −18 °С. В некоторый момент машину запустили в обратном направлении, так что все составляющие теплового баланса — работа и количества теплоты — поменяли свои знаки. При этом за счёт работы, совершенной двигателем тепловой машины, от холодного тела теплота стала отбираться, а тёплому телу — сообщаться.
Какую работу совершил двигатель тепловой машины, если количество теплоты, отведенной от холодного тела, равно 165 кДж? Ответ округлите до целого числа кДж.
КПД идеальной тепловой машины равен отношению совершенной работы к затраченному количеству теплоты где и — температуры «нагревателя» (теплого тела) и «холодильника» (холодного тела), с которыми обменивается теплотой рабочее вещество цикла. Количество теплоты, которое при этом отдается холодильнику, равно
При работе идеальной тепловой машины в обратном направлении от холодного тела отнимается количество теплоты за счет работы совершаемой над рабочим веществом цикла, и теплому телу, которым в данном случае является окружающая среда, отдается количество теплоты причем все соотношения количеств теплоты, работы и температур остаются такими же, как при работе идеальной тепловой машины в прямом направлении.
Здравствуйте! Поправьте меня, если я неправильно понял смысл задачи, но на мой взгляд тут явно ошибки в формулировках. В тексте задачи ставится вопрос: "Какую работу совершил двигатель тепловой машины. ". При работе тепловой машины в обратную сторону мы имеем то что описано в решении: ". от холодного тела отнимается количество теплоты Q- за счет работы A, совершаемой над рабочим веществом. ". Всё верно, и так как совершается работа НАД рабочим веществом, то, стало быть, работа САМОГО вещества будет отрицательной. А если мы теперь заглянем в ответ, то увидим там положительный результат. Таким образом, из данного решения следует, что двигатель, отняв теплоту от более холодного тела (тем самым ещё сильнее охладив его), и передав его более горячему (ещё сильнее нагрев его), помимо прочего ещё и совершил ПОЛОЖИТЕЛЬНУЮ работу. Это противоречит обоим постулатам Клаузиуса и Кельвина! Пожалуйста, объясните где я ошибся в рассуждениях, или это неверно составленное решение?
Для холодильника в формуле КПД холодильника работа выполняется внешними силами, а не газом.
Идеальная тепловая машина обменивается теплотой с тёплым телом — окружающей средой, находящейся при температуре +25 °С, и холодным телом с температурой –18 °С. В некоторый момент машину запустили в обратном направлении, так что все составляющие теплового баланса — работа и количества теплоты — поменяли свои знаки. При этом за счёт работы, совершённой двигателем тепловой машины, от холодного тела теплота стала отбираться, а тёплому телу — сообщаться.
Какую работу совершил двигатель тепловой машины, если количество теплоты, сообщенной тёплому телу, равно 193 кДж? Ответ округлите до целого числа кДж.
КПД идеальной тепловой машины равен отношению совершенной работы к затраченному количеству теплоты где и — температуры «нагревателя» (теплого тела) и «холодильника» (холодного тела), с которыми обменивается теплотой рабочее вещество цикла. Количество теплоты, которое при этом отнимается от теплого тела, равно
При работе идеальной тепловой машины в обратном направлении от холодного тела отнимается количество теплоты за счёт работы совершаемой над рабочим веществом цикла, и тёплому телу, которым в данном случае является окружающая среда, отдается количество теплоты причём все соотношения количеств теплоты, работы и температур остаются такими же, как при работе идеальной тепловой машины в прямом направлении.
67. Азот, находившийся при температуре 400 К, подвергли адиабатическому расширению, в результате которого его объем увеличился в n = 5 раз, а внутренняя энергия уменьшилась на 4 кДж. Определите массу азота.
68. Двухатомный идеальный газ занимает объем V1 = 1 л и находится под давлением p1 = 0,1 МПа. После адиабатического сжатия газ занимает объем V2 и создает давление p2. В результате последующего изохорического процесса газ охлаждается до первоначальной температуры, а его давление p3 = 0,2 МПа. Определите: 1) объем V2 ; 2) давление p2. Начертите график этих процессов.
69. Кислород, занимающий при давлении p1 = 1 МПа объем V1 = 5 л, расширяется в n = 3 раза. Определите конечное давление и работу, совершенную газом в случае: 1) изобарного; 2) изотермического; 3) адиабатического процессов.
70. Кислород массой 10 г, находящийся при температуре 370 К, подвергли адиабатному расширению, в результате которого его давление уменьшилось в n= 4 раза. В результате последующего изотермического процесса газ сжимается до первоначального давления. Определите: 1) температуру газа в конце процесса; 2) количество теплоты, отданное газом; 3) приращение внутренней энергии газа; 4) работу, совершенную газом.
71. Идеальный двухатомный газ, занимающий объем V1 = 2 л, подвергли адиабатному расширению. При этом его объем возрос в 5раз. Затем газ подвергли изобарному сжатию до начального объема В результате изохорного нагревания он был возвращен в первоначальное состояние. Постройте график цикла и определите термический КПД цикла.
72. Идеальный двухатомный газ (ν=3 моль), занимающий объем V1 = 5 л и находящийся под давлением p1 = 1 МПа, подвергли изохорному нагреванию до Т2 = 500 К. После этого газ подвергли изотермическому расширению до начального давления, а затем он в результате изобарического сжатия был возвращен в первоначальное состояние. Постройте график цикла и определите термический КПД цикла.
73. Рабочее тело – идеальный газ – совершает в тепловом двигателе цикл, состоящий из последовательных изобарического, адиабатического и изотермического процессов. В результате изобарного процесса газ нагревается от Т1 = 300 К до Т2 = 600 К. Определите термический КПД теплового двигателя.
74. Азот массой 500 г, находящийся под давлением p1 = 1 МПа при температуре t1 = 127 °С, подвергли изотермическому расширению, в результате которого давление газа уменьшилось в n = 3 раза. После этого газ подвергли адиабатному сжатию до начального давления, а затем он был изобарно сжат до начального объема. Постройте график цикла и определите работу, совершенную газом за цикл.
75. Идеальный газ, совершающий цикл Карно, 70% количества теплоты, полученного от нагревателя, отдает холодильнику. Количество теплоты, получаемое от нагревателя, равно 5 кДж. Определите: 1) термический КПД цикла; 2) работу, совершенную при полном цикле.
76. Идеальный газ совершает цикл Карно. Газ получил от нагревателя количество теплоты 5,5 кДж и совершил работу 1,1 кДж. Определите: 1) термический КПД цикла; 2) отношение температур нагревателя и холодильника.
77. Идеальный газ совершает цикл Карно, термический КПД которого равен 0,4. Определите работу изотермического сжатия газа, если работа изотермического расширения составляет 400 Дж.
78. Идеальный газ совершает цикл Карно. Температура нагревателя Т1 = 500 К, холодильника Т2 = 300 К. Работа изотермического расширения газа составляет 2 кДж. Определите: 1) КПД цикла; 2) количество теплоты и отданное газом при изотермическом сжатии холодильнику.
79. Многоатомный идеальный газ совершает цикл Карно, при этом в процессе адиабатного расширения объем газа увеличивается в n = 4 раза. Определите КПД цикла.
80. Во сколько раз необходимо увеличить объем (ν = 5 моль) идеального газа при изотермическом расширении, если его энтропия увеличилась на ΔS = 57,6 Дж/К?
81. При нагревании двухатомного идеального газа (ν = 2 моль) его термодинамическая температура увеличилась в n = 2 раза. Определите изменение энтропии, если нагревание происходит: 1) изохорно; 2) изобарно.
82. Идеальный газ (ν = 2 моль) сначала изобарно нагрели, так что объем газа увеличился в n = 2 раза, а затем изохорно охладили, так что давление его уменьшилось в n = 2 раза. Определите приращение энтропии в ходе указанных процессов.
83. Азот массой 28 г адиабатно расширили в n = 2 раза, а затем изобарно сжали до начального объема. Определите изменение энтропии газа в ходе указанных процессов.
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами - загрузи их здесь!
Температуру нагревателя тепловой машины Карно понизили, оставив температуру холодильника прежней. Количество теплоты, отданное газом холодильнику за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл?
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
КПД тепловой машины Карно вычисляется по формуле:
В идеальном тепловом двигателе увеличилась работа совершаемая газом за один цикл
Температуру холодильника идеальной тепловой машины увеличили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины, количество теплоты, отданное газом за цикл холодильнику, и работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
холодильнику за цикл работы
Если повысить температуру холодильника при неизменной температуре нагревателя, КПД идеальной тепловой машины уменьшится:
КПД связано с работой газа и количеством теплоты, полученным газом за цикл, соотношением Таким образом, при повышении температуры холодильника работа газа за цикл уменьшится. Отданное холодильнику количество теплоты можно найти из закона сохранения энергии: Так как после повышения температуры холодильника количество теплоты останется неизменным, а работа уменьшится, количество теплоты, отданное холодильнику за цикл работы, увеличится.
В идеальном тепловом двигателе увеличилась работа совершаемая газом за один цикл
Задание 11. Температуру холодильника теплового двигателя, работающего по циклу Карно, увеличили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД теплового двигателя и количество теплоты, отданное газом за цикл холодильнику?
Для каждой величины определите соответствующий характер изменения:
3) не изменилась
КПД теплового двигателя в цикле Карно описывается выражением
По условию задачи температура
, а температуру увеличили. В соответствии с приведенной формулой КПД двигателя уменьшается. А соотношение первой и второй формул КПД показывает, что величина должна увеличиться.
В идеальном тепловом двигателе увеличилась работа совершаемая газом за один цикл
Температура нагревателя тепловой машины 800 К, температура холодильника в 2 раза меньше, чем у нагревателя. Каков максимально возможный КПД машины? (Ответ дайте в процентах.)
Температура холодильника равна
Максимально возможный КПД тепловой машины равен КПД машины Карно
Температура нагревателя тепловой машины 900 К, температура холодильника в 3 раза меньше, чем у нагревателя. Каков максимально возможный КПД машины? (Ответ дайте в процентах, округлив до целых.)
Температура холодильника равна
Максимально возможный КПД тепловой машины равен КПД машины Карно
В тепловой машине температура нагревателя 600 K, температура холодильника на 200 К меньше, чем у нагревателя. Максимально возможный КПД машины? (Ответ дайте в процентах, округлив до целых.)
Температура холодильника равна
Максимально возможный КПД тепловой машины равен КПД машины Карно
Какое из перечисленных ниже действий при прочих неизменных условиях ведёт к уменьшению КПД идеального теплового двигателя?
1) повышение температуры нагревателя
2) повышение температуры холодильника
3) уменьшение трения в механизме тепловой машины
4) замена рабочего тела
КПД идеального теплового двигателя рассчитывается по формуле
Следовательно, при повышении температуры холодильника уменьшается КПД теплового двигателя.
Правильный ответ указан под номером 2.
Идеальная тепловая машина работает с использованием цикла Карно. Температуру холодильника машины понижают, при этом температура нагревателя и количество теплоты, которое рабочее тело получает от нагревателя за один цикл, остаются неизменными. Как изменяются в результате этого КПД тепловой машины и совершаемая машиной за один цикл работа?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Для КПД цикла Карно справедлива формула:
Отсюда видно, что при уменьшении температуры холодильника, КПД тепловой машины увеличится, а значит, увеличится полезная работа, совершаемая за один цикл.
Идеальная тепловая машина работает с использованием цикла Карно. Температуру холодильника машины повышают, при этом температура нагревателя и количество теплоты, которое рабочее тело получает от нагревателя за один цикл, остаются неизменными. Как изменяются в результате этого КПД тепловой машины и совершаемая машиной за один цикл работа?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Для КПД цикла Карно справедлива формула:
Отсюда видно, что при увеличении температуры холодильника, КПД тепловой машины уменьшится, а значит, уменьшится полезная работа, совершаемая за один цикл.
Тепловая машина работает по циклу Карно. Температуру холодильника тепловой машины повысили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| КПД тепловой машины | Работа газа за цикл |
КПД машины Карно
при увеличении температуры холодильника уменьшается.
Работа газа за цикл
Идеальная тепловая машина использует в качестве рабочего тела 1 моль идеального одноатомного газа. Установите соответствие между КПД этой тепловой машины и соотношением между физическими величинами в циклическом процессе. К каждой позиции первого столбца подберите соответствующую позицию второго столбца.
1) Работа, совершаемая газом, 20 Дж; количество теплоты, полученное газом, 80 Дж.
2) Количество теплоты, отданное газом, 20 Дж; количество теплоты, полученное газом, 100 Дж.
3) Температура холодильника 300 К; температура нагревателя 375 К.
4) Разность температур нагревателя и холодильника 300 К; температура нагревателя 400 К.
ФИЗИЧЕСКИМИ ВЕЛИЧИНАМИ В ЭТОМ
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Работу, совершаемую газом можно вычислить по формуле:
КПД можно вычислить по формуле:
1) увеличилось 2) уменьшилось 2) не изменилось
- Температура нагревателя идеального теплового двигателя, работающего по циклу Карно, равна T1, а температура холодильника равна T2. За цикл двигатель получает от нагревателя количество теплоты Q1. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
- В идеальном тепловом двигателе уменьшилась полезная мощность, при неизменном количестве теплоты, получаемой за один цикл от нагревателя. Как при этом изменятся коэффициент полезного действия цикла, количество теплоты, отдаваемое за один цикл холодильнику и температура холодильника? Для каждой величины определите соответствующий характер изменения:
1) увеличилось 2) уменьшилось 2) не изменилось
- Температура нагревателя 227 0С. Определите КПД идеального двигателя и температуру холодильника, если за счет каждого килоджоуля теплоты, полученной от нагревателя, двигатель совершает механическую работу 350 Дж. (35%; 520С)
- Один моль одноатомного газа совершает цикл, состоящий из двух изохор и двух изобар. При этом максимальное давление в 2 раза больше минимального, а максимальный объём в 3 раза больше минимального. Определите коэффициент полезного действия цикла. (17%)
- КПД идеальной тепловой машины, работающей по циклу Карно, равен 40%. Как и во сколько раз необходимо изменить количество отведенного холодильнику тепла, чтобы без изменения количества подводимого тепла КПД возросло до 70%. (уменьшить в 2 раза)
- С одним молем идеального одноатомного газа совершают циклический процесс 1-2-3-4-1 (см. рис.). Во сколько раз n КПД данного цикла меньше, чем КПД идеальной тепловой машины, работающей при тех же максимальной и минимальной температурах? (12)

Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-04-27 Нарушение авторских прав и Нарушение персональных данных
Молекулярно-кинетическая теория
Теория к заданию №12 ЕГЭ по физике
КПД тепловой машины
Адиабатный процесс
Адиабатный (адиабатический) процесс связан с первым термодинамическим законом. При нем изменение теплоты в системе равно сумме изменений тепловой энергии и выполненной работы, которую выполняет газ. Он протекает без передачи газу теплоты. Не происходит и передача теплоты газом внешней среде. Адиабатический процесс графически изображается так:
Разбор типовых вариантов № 12 ЕГЭ по физике
Демонстрационный вариант 2018
Тепловая машина работает по циклу Карно. Температуру холодильника тепловой машины повысили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
- увеличилась,
- уменьшилась,
- не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Работа газа за цикл
Алгоритм решения:
- Записываем формулу расчета КПД. Анализируем, что произойдет, если температуру нагревателя увеличить.
- Записываем формулу для КПД, выраженного через работу. Анализируем, как изменится эта величина.
- Записываем ответ.
Решение:
1. Для любого двигателя показатель КПД определяется формулой:
3. Заполняем таблицу:
| КПД тепловой машины | Работа газа за цикл |
| 2 | 2 |
Первый вариант задания (Демидова, №3)
| ГРАФИКИ | УТВЕРЖДЕНИЯ 1) Над газом совершают работу, при этом его внутренняя энергия увеличивается. 2) Над газом совершают работу, при этом газ отдаёт положительное количество теплоты. 3) Газ получает положительное количество теплоты и совершает работу. 4) Газ получает положительное количество теплоты, при этом его внутренняя энергия увеличивается. |
Алгоритм решения:
- Рассматриваем первый график таблицы. Ищем правильное предложение в графе справа.
- Проводим анализ второго графика в левой графе таблицы. Определяем правильный ответ в графе справа.
- Записываем ответ.
Решение:
1. На графике А) температура повышается, но объем не изменяется. Это изохорный процесс, поэтому газ не совершает работы, и над газом работа не совершается. Поскольку темп-ра увеличивается (происходит нагревание), газ получает некоторое кол-во теплоты. Из 1-го з-на термодинамики (Q=∆U+A) следует, что его внутр.энергия возрастает. Анализируем утверждения: 1) Утверждение 1 неверно в своей первой части; 2) Утверждение 2 неверно полностью; 3) Утверждение 3 неверно в своей 2-й части; 4) Утверждение 4 верно.
2. Вариант Б) показывает: уменьшаются показатели объема газа и давления. Происходит сжатие газа; это означает, что над газом производится работа. Применив ур-ние Менделеева-Клапейрона (pV=νRT), делаем вывод: при снижении объема и давления должна снижаться и температура. А из этого утверждения в свою очередь следует, что снижается внутр.энергия газа. Кол-во теплоты (положительное) при этом отдается. Работа над газом в данном случае совершается. Анализируем утверждения: 1) Утверждение 1 неверно во 2-й своей части; 2) Утверждение 2 верно; 3) Утверждения 3 и 4 неверны полностью.
Второй вариант задания (Демидова, №20)
| ПРОЦЕССЫА) изохорный процесс при N = const Б) адиабатный процесс при N = const | ФОРМУЛЫ |
Алгоритм решения:
- Анализируем, что происходит при изохорном типе процесса. Определяем, какой вариант равенств соответствует такому процессу.
- Анализируем, каким образом происходит адиабатический процесс. Устанавливаем, какое равенство соответствует данному процессу.
- Записываем ответ.
Решение:
1. Справа вариантом А) записано, что происходит изохорный процесс. Он совершается при постоянном показателе объема. В этом случае действует з-н Шарля: р/Т= const. Такое равенство стоит под 1-м номером.
2. При адиабатическом процессе Б) не происходит теплового обмена со средой, то есть выполняется равенство: Q=0. Значит, правильные предложения 1 и 4.
Второе начало термодинамики возникло из анализа работы тепловых двигателей (машин). В формулировке Кельвина оно выглядит следующим образом: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.
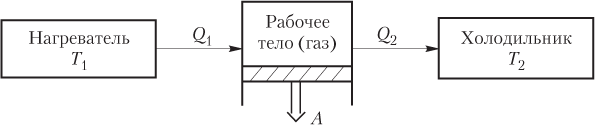
Схема действия тепловой машины (теплового двигателя) представлена на рис. 6.3.
Цикл работы теплового двигателя состоит из трех этапов:
1) нагреватель передает газу количество теплоты Q 1 ;
2) газ, расширяясь, совершает работу A ;
3) для возвращения газа в исходное состояние холодильнику передается теплота Q 2 .
Из первого закона термодинамики для циклического процесса
где Q — количество теплоты, полученное газом за цикл, Q = Q 1 − Q 2 ; Q 1 — количество теплоты, переданное газу от нагревателя; Q 2 — количество теплоты, отданное газом холодильнику.
Поэтому для идеальной тепловой машины справедливо равенство
Когда потери энергии (за счет трения и рассеяния ее в окружающую среду) отсутствуют, при работе тепловых машин выполняется закон сохранения энергии
где Q 1 — теплота, переданная от нагревателя рабочему телу (газу); A — работа, совершенная газом; Q 2 — теплота, переданная газом холодильнику.
Коэффициент полезного действия тепловой машины вычисляется по одной из формул:
η = A Q 1 ⋅ 100 % , η = Q 1 − Q 2 Q 1 ⋅ 100 % , η = ( 1 − Q 2 Q 1 ) ⋅ 100 % ,
где A — работа, совершенная газом; Q 1 — теплота, переданная от нагревателя рабочему телу (газу); Q 2 — теплота, переданная газом холодильнику.
Наиболее часто в тепловых машинах используется цикл Карно , так как он является самым экономичным.
Цикл Карно состоит из двух изотерм и двух адиабат, показанных на рис. 6.4.
Участок 1–2 соответствует контакту рабочего вещества (газа) с нагревателем. При этом нагреватель передает газу теплоту Q 1 и происходит изотермическое расширение газа при температуре нагревателя T 1 . Газ совершает положительную работу ( A 12 > 0), его внутренняя энергия не изменяется (∆ U 12 = 0).
Участок 2–3 соответствует адиабатному расширению газа. При этом теплообмена с внешней средой не происходит, совершаемая положительная работа A 23 приводит к уменьшению внутренней энергии газа: ∆ U 23 = − A 23 , газ охлаждается до температуры холодильника T 2 .
Участок 3–4 соответствует контакту рабочего вещества (газа) с холодильником. При этом холодильнику от газа поступает теплота Q 2 и происходит изотермическое сжатие газа при температуре холодильника T 2 . Газ совершает отрицательную работу ( A 34 < 0), его внутренняя энергия не изменяется (∆ U 34 = 0).
Участок 4–1 соответствует адиабатному сжатию газа. При этом теплообмена с внешней средой не происходит, совершаемая отрицательная работа A 41 приводит к увеличению внутренней энергии газа: ∆ U 41 = − A 41 , газ нагревается до температуры нагревателя T 1 , т.е. возвращается в исходное состояние.
Коэффициент полезного действия тепловой машины, работающей по циклу Карно, вычисляется по одной из формул:
η = T 1 − T 2 T 1 ⋅ 100 % , η = ( 1 − T 2 T 1 ) ⋅ 100 % ,
где T 1 — температура нагревателя; T 2 — температура холодильника.
Пример 9. Идеальная тепловая машина совершает за цикл работу 400 Дж. Какое количество теплоты передается при этом холодильнику, если коэффициент полезного действия машины равен 40 %?
Решение . Коэффициент полезного действия тепловой машины определяется формулой
где A — работа, совершаемая газом за цикл; Q 1 — количество теплоты, которое передается от нагревателя рабочему телу (газу).
Искомой величиной является количество теплоты Q 2 , переданное от рабочего тела (газа) холодильнику, не входящее в записанную формулу.
Связь между работой A , теплотой Q 1 , переданной от нагревателя газу, и искомой величиной Q 2 устанавливается с помощью закона сохранения энергии для идеальной тепловой машины
Уравнения образуют систему
η = A Q 1 ⋅ 100 % , Q 1 = A + Q 2 , >
которую необходимо решить относительно Q 2 .
Для этого исключим из системы Q 1 , выразив из каждого уравнения
Q 1 = A η ⋅ 100 % , Q 1 = A + Q 2 >
и записав равенство правых частей полученных выражений:
A η ⋅ 100 % = A + Q 2 .
Искомая величина определяется равенством
Q 2 = A η ⋅ 100 % − A = A ( 100 % η − 1 ) .
Расчет дает значение:
Q 2 = 400 ⋅ ( 100 % 40 % − 1 ) = 600 Дж.
Количество теплоты, переданной за цикл от газа холодильнику идеальной тепловой машины, составляет 600 Дж.
Пример 10. В идеальной тепловой машине от нагревателя к газу поступает 122 кДж/мин, а от газа холодильнику передается 30,5 кДж/мин. Вычислить коэффициент полезного действия данной идеальной тепловой машины.
Решение . Для расчета коэффициента полезного действия воспользуемся формулой
η = ( 1 − Q 2 Q 1 ) ⋅ 100 % ,
где Q 2 — количество теплоты, которое передается за цикл от газа холодильнику; Q 1 — количество теплоты, которое передается за цикл от нагревателя рабочему телу (газу).
Преобразуем формулу, выполнив деление числителя и знаменателя дроби на время t :
η = ( 1 − Q 2 / t Q 1 / t ) ⋅ 100 % ,
где Q 2 / t — скорость передачи теплоты от газа холодильнику (количество теплоты, которое передается газом холодильнику в секунду); Q 1 / t — скорость передачи теплоты от нагревателя рабочему телу (количество теплоты, которое передается от нагревателя газу в секунду).
В условии задачи скорость передачи теплоты задана в джоулях в минуту; переведем ее в джоули в секунду:
- от нагревателя газу —
Q 1 t = 122 кДж/мин = 122 ⋅ 10 3 60 Дж/с ;
- от газа холодильнику —
Q 2 t = 30,5 кДж/мин = 30,5 ⋅ 10 3 60 Дж/с .
Рассчитаем коэффициент полезного действия данной идеальной тепловой машины:
η = ( 1 − 30,5 ⋅ 10 3 60 ⋅ 60 122 ⋅ 10 3 ) ⋅ 100 % = 75 % .
Пример 11. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, равен 25 %. Во сколько раз увеличится коэффициент полезного действия, если температуру нагревателя увеличить, а температуру холодильника уменьшить на 20 %?
Решение . Коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, определяется следующими формулами:
- до изменения температур нагревателя и холодильника —
η 1 = ( 1 − T 2 T 1 ) ⋅ 100 % ,
где T 1 — первоначальная температура нагревателя; T 2 — первоначальная температура холодильника;
- после изменения температур нагревателя и холодильника —
η 2 = ( 1 − T ′ 2 T ′ 1 ) ⋅ 100 % ,
где T ′ 1 — новая температура нагревателя, T ′ 1 = 1,2 T 1 ; T ′ 2 — новая температура холодильника, T ′ 2 = 0,8 T 2 .
Уравнения для коэффициентов полезного действия образуют систему
η 1 = ( 1 − T 2 T 1 ) ⋅ 100 % , η 2 = ( 1 − 0,8 T 2 1,2 T 1 ) ⋅ 100 % , >
которую необходимо решить относительно η 2 .
Из первого уравнения системы с учетом значения η 1 = 25 % найдем отношение температур
T 2 T 1 = 1 − η 1 100 % = 1 − 25 % 100 % = 0,75
и подставим во второе уравнение
η 2 = ( 1 − 0,8 1,2 ⋅ 0,75 ) ⋅ 100 % = 50 % .
Искомое отношение коэффициентов полезного действия равно:
η 2 η 1 = 50 % 25 % = 2,0 .
Следовательно, указанное изменение температур нагревателя и холодильника тепловой машины приведет к увеличению коэффициента полезного действия в 2 раза.
Тепловая машина работает по циклу Карно. Температуру холодильника тепловой машины повысили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл? Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
А) КПД находится по формуле: \[\eta =1-\dfrac
Так как температуру холодильника повысили, а нагревателя не изменили, то КПД уменьшился.
Б) С другой стороны КПД равен: \[\eta =\dfrac\] Так как количество теплоты, полученное газом от нагревателя за цикл, не изменилось, то работа газа уменьшилась
Температуру холодильника тепловой машины Карно понизили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл? Для каждой величины определите соответствующий характер её изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
А) КПД находится по формуле: \[\eta =1-\dfrac
Так как температуру холодильника понизили, а нагревателя не изменили, то КПД увеличился.
Б) С другой стороны КПД равен: \[\eta =\dfrac\] Так как количество теплоты, полученное газом от нагревателя за цикл, не изменилось, то работа газа увеличилась.
Температура нагревателя идеального теплового двигателя, работающего по циклу Карно, равна \(T_1\) , а коэффициент полезного действия этого двигателя равен \(\eta\) . За цикл рабочее тело двигателя получает от нагревателя количество теплоты \(Q_1\) . Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
А) КПД равно \[\eta = 1- \dfrac
Температуру нагревателя тепловой машины Карно понизили, оставив температуру холодильника прежней. Количество теплоты, отданное газом холодильнику за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл? Для каждой величины определите соответствующий характер её изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
“Досрочная волна 2020 вариант 1”
А) КПД находится по формуле: \[\eta =1-\dfrac
Так как температуру нагревателя понизили, то КПД уменьшился Б) С другой стороны КПД равен: \[\eta =\dfrac=\dfrac
Температуру холодильника идеальной тепловой машины уменьшили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и количество теплоты, отданное газом за цикл холодильнику?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
КПД тепловой машины — 1
1)КПД цикла Карно: \[\eta=1-\dfrac
При уменьшении температуры холодильника КПД увеличивается.
Количество теплоты, отданное газом — 2
2) Так как КПД увеличился и количество теплоты, полученное газом от нагревателя за цикл, не изменилось, то количество теплоты, отданное газом — уменьшилось.
Температуру холодильника идеальной тепловой машины уменьшили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом количество теплоты, отданное газом за цикл холодильнику, и работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Количество теплоты, отданное газом — 2
1)КПД цикла Карно: \[\eta=1-\dfrac
Так как КПД увеличился и количество теплоты, полученное газом от нагревателя за цикл, не изменилось, то количество теплоты, отданное газом — уменьшилось.
Работа газа за цикл — 1
2) Работу, совершенную газом за цикл, можно найти по формуле: \[A_\text<ц>=Q_<\text<н>>-Q_<\text<х>>\] Так как количество теплоты, полученное газом от нагревателя за цикл, не изменилось, а количество теплоты, переданное холодильнику, уменьшилось, то работа газа за цикл увеличилась.
Как изменяется внутренняя энергия идеального газа и его давление при его изотермическом расширении?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Внутренняя энергия — 3
1) Изменение внутренней энергии равно: \[\Delta U=\dfrac<3><2>\nu R\Delta T,\] где \(\nu\) — количество вещеста газа, \(R\) — универасальная газовая постоянная, \(\Delta T\) — изменение температуры газа.
Так как процесс изотермический, то \(\Delta T=0\) , то есть \(\Delta U=0\) .
Давление — 2
2)Так как процесс изотермический, то по закону Бойля-Мариотта: \[pV=const\] Значит, при увеличении объема давление газа уменьшается.
Какую работу совершат 6 кг воздуха, расширяясь при изобарическом нагреве от 5◦С до 150◦С? Ответ округлите до целых. Ответ выразите в (кДж).
На pV -диаграмме представлен процесс изменения состояния идеального одноатомного газа. Масса газа не меняется. Какую работу совершает газ при переходе из состояния 1 в состояние 3?…
На pT -диаграмме представлен процесс изменения состояния идеального одноатомного газа. Масса газа не меняется. Какую работу совершают внешние силы при переходе газа из состояния 1 …
Какую работу совершил газ при переходе из состояния 1 в состояние 3? Ответ выразите в (·p0V0).
При изобарном расширении идеальный двухатомный газ получил количество теплоты, равное 800 Дж. Насколько увеличилась внутренняя энергия газа при этом процессе? Ответ выразите в (Дж)…
Какова внутренняя энергия гелия, заполняющего аэростат объёмом 60 м 3 при давлении 100 кПа? Ответ выразите в (МДж).
Аргону сообщили 30 кДж теплоты, и он изобарно расширился. При этом объём газа увеличился на 0,6 м 3 . Каково давление газа? Ответ выразите в (кПа).
В сосуде с постоянным объёмом охлаждают идеальный одноатомный газ, причём количество отведённого тепла равно 300 Дж. Определите объём сосуда, если давление в нём понизилось на 100 …
В изобарном процессе при нормальном атмосферном давлении объём газа увеличился от 5 л до 7 л. Чему равно приращении внутренней энергии газа в данном процессе? Ответ в Дж.
Газ совершает процесс, при котором работа газа равна убыли его внутренней энергии. Что это за процесс? Ответ запишите словом.
Каков КПД идеальной тепловой машины, работающей в интервале температур 100 $°$С–400 $°$С?Ответ выразите в процентах и округлите до целых. Ответ в %.
За цикл тепловая машина получила 100 Дж теплоты. Найдите, сколько теплоты получил холодильник, если коэффициент полезного действия этой машины 24%. Ответ в Дж.
Один моль идеального одноатомного газа сначала изотермически сжали при температуре 270 К до объёма 0,831 м 3 . Затем газ изохорно охладили, понизив давление в 2 раза. Какую работу со…
Какое количество теплоты получает идеальный одноатомный газ в изобарном процессе, если он совершает работу против внешних сил, равную 2 кДж? Ответ в кДж.
Какую работу совершает газ в ходе изохорического процесса, если он при этом отдаёт 3,6 кДж тепла? Ответ в кДж.
Каков КПД тепловой машины, работающей по циклу Карно, если отношение работы изотермического расширения к модулю работы изотермического сжатия равно 4? Ответ в %.
Температура нагревателя идеальной тепловой машины 600$°$C, а холодильника 100$°$C. Чему равен её коэффициент полезного действия? Ответ выразите в процентах и округлите до целых. Ответ …
На рисунке приведён график зависимости давления неизменной массы газа от температуры. Изменения происходят в направлении указанном стрелками. Какой процесс происходит с газом на уч…
Каково давление одноатомного идеального газа, занимающего объём 2 л, если его внутренняя энергия равна 300 Дж? Ответ в кПа.
На рисунке представлен график процесса в координатах $pT$. Какой вид имеет этот график в координатах $pV$?

КПД тепловой машины можно вычислить как
Машина получает тепло только на участке AB, и, так как работы здесь не совершается, то можно вычислить количество теплоты, полученное газом, как увеличение его внутренней энергии:
Работа численно равна площади, ограниченной циклом. Поэтому
Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и , и , это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать . Но, так как , а ,то изменение внутренней энергии будет равно
Определим максимальный КПД. Посчитаем его как КПД цикла Карно. Максимальная температура газа будет достигнута в точке , а минимальная – в точке :
Ответ: , .
Задача 2. Над идеальным одноатомным газом проводят цикл, включающий изобару, изохору, изотерму, при этом работа газа за цикл равна кДж. В процессе изотермического сжатия (3-1) внешние силы совершают над газом положительную работу кДж. Найдите КПД данной тепловой машины.

Работа газа в процессе 1-2– площадь под линией процесса 1-2. Работа внешних сил – площадь под циклом (под линией 3-1). Поэтому полная работа за цикл – это разность работы газа и работы внешних сил, площадь, ограниченная линиями цикла. Она будет равна 5 кДж.
Работа газа в процессе 1-2, таким образом, равна 8 кДж. А поскольку процесс изобарный, то кДж. Тогда КПД
Ответ: .
Задача 3. КПД тепловой машины, работающей по циклу, включающему изотермический (1-2) и адиабатный (3-1) процессы, равен , причем работа, совершенная 2 моль одноатомного идеального газа в изотермическом процессе кДж. Найдите разность максимальной и минимальной температур газа в цикле.
Это задание также относится к высокому уровню сложности. Как правило, тематика этого задания «МКТ» и «Термодинамика». Какие-то задачи требуют только формульного решения, какие-то необходимо сопровождать графическими пояснениями термодинамических процессов. В любом случае, теоретический материал полностью соответствует кодификатору элементов содержания и спецификации контрольных измерительных материалов.
1. В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол при температуре кипения При сообщении бензолу некоторого количества теплоты часть его превращается в пар, который при изобарном расширении совершает работу, поднимая поршень. Удельная теплота парообразования бензола Дж/кг, а его молярная масса кг/моль. Какая часть подводимого к бензолу количества теплоты идёт на увеличение внутренней энергии системы? Объёмом жидкого бензола и трением между поршнем и цилиндром пренебречь.
Запишем первый закон термодинамики для изобарного процесса:
Выразим из этого равенства изменение внутренней энергии:
Работу газа в изобарном процессе можно рассчитать по формуле:
с учетом уравнения Менделеева-Клапейрона получим:
(2).
При совершении работы давление бензола не изменяется, так как поршень в цилиндре легкоподвижный. Давление бензола все время остается равным атмосферному.
При этом
– масса бензола, превратившегося в газообразное состояние.
Количество теплоты, которое идет на превращение бензола в это состояние можно рассчитать по формуле:
Выражение для работы бензола (2) и количества теплоты (3) подставим в уравнение (1).
После сокращения на получим искомую формулу:
Подставим численные значения и проведем расчет:
Секрет решения. На первый взгляд задача кажется несложной, но в ней «спрятаны» несколько искусственных приемов, до которых додуматься достаточно сложно. Первый прием – выражение Это математический ход, который сразу подсказывает, что конкретно надо находить в этой задаче.
Второй прием – получение равенства, используя уравнения Менделеева-Клапейрона Здесь надо придерживаться следующих рассуждений: если в левой части уравнения есть переменная величина (в этой задаче ), то и в правой части должна изменяться какая-то физическая величина (в этой задаче ). Можно сказать еще проще: если в левой части равенства есть знак дельта " ", то и в правой части он должен обязательно появиться. В крайнем случае, можно «перебрать» все величины из правой части: температура не может изменяться, так как при парообразовании она всегда постоянна; молярная масса также неизменна, потому что речь идет об одном и том же газе; R – табличная величина. Остается только Эти рассуждения помогут понять ситуацию, описанную в задаче и правильно ее решить.
2. Одно и то же постоянное количество одноатомного идеального газа расширяется из одного и того же начального состояния до одного и того же конечного объёма первый раз по изобаре 1–2, а второй по адиабате 1–3 (см. рисунок). Отношение работы газа в процессе 1–2 к работе газа в процессе 1–3 равно =к=2. Чему равно отношение х количества теплоты полученного газом от нагревателя в ходе процесса 1–2, к модулю изменения внутренней энергии газа в ходе процесса 1–3?

Для участка 1–2 применим первый закон термодинамики с учетом изобарного процесса.
Работу газа при расширении найдем как площадь прямоугольника под графиком.
Изменение внутренней энергии одноатомного идеального газа запишем в виде формулы:
Применим уравнение Менделеева-Клапейрона:
Тогда (3) примет вид:
Таким образом количество теплоты на участке 12 равно:
Для участка 1–3 применим первый закон термодинамики с учетом адиабатного процесса.
но так как запишем:
или Это выражение означает, что газ на участке 13 совершает работу за счет уменьшения своей внутренней энергии.
Учтем, что по условию =к=2, тогда:
Используя (5) и (6) получим искомую формулу:
Секрет решения. Несмотря на громоздкие расчеты и обилие разных индексов в уравнениях, задача является среднего уровня сложности. Надо знать:
- первый закон термодинамики;
- его применение к изопроцессам;
- формулы, выражающие работу газа и его внутреннюю энергию (только для одноатомного идеального газа);
- уметь «читать» графики;
- понимать, что при расширении газ совершает положительную работу, при сжатии – отрицательную работу;
- проводить рассуждения о том, откуда газ берет энергию для совершения работы (за счет своей внутренней энергии или за счет поступления энергии извне);
- указанные пункты описывать соответствующими уравнениями.
Суть любой задачи по физике – описание физических процессов математическими уравнениями, которые надо решить удобным (рациональным) способом.
3. В тепловом двигателе 1 моль одноатомного разряженного газа совершает цикл 1–2–3–4–1, показанный на графике в координатах p–T, где p – давление газа, Т – абсолютная температура. Температуры в точках 2 и 4 равны и превышают температуру в точке 1 в 2 раза. Определите КПД цикла. 
КПД теплового двигателя определяется формулой:
– полезная работа, совершенная газом за цикл, Q – полученное за цикл количество теплоты. Можно графически рассчитать работу, если перерисовать данный цикл в координатах рV. Проведем анализ каждого процесса.
В координатах рV график будет иметь вид:

Работа газа за цикл будет определяться площадью прямоугольника 1-2-3-4.
Поэтому (на основании закона Шарля).
(на основании закона Гей-Люссака).
Таким образом, можно выразить полезную работу через и
Газ получает положительное количество теплоты на участках 1–2 и 2–3.
Применим к этим участкам первый закон термодинамики.
Но работа газа на этом участке равна нулю, так как процесс изохорный.
С учетом уравнения Менделеева-Клапейрона и получим:
Для участка 23 первый закон термодинамики примет вид:
Работа определяется площадью прямоугольника под участком 23.
С учетом уравнения Менделеева-Клапейрона (4) примет вид:
Таким образом, полученное количество теплоты на участке 23 равно:
Общее количество теплоты, полученное за цикл:
Полученные выражения из (1) и (6) подставим в формулу КПД.
Секрет решения. За задачи на определение КПД тепловой машины по графику надо получать максимальные 3 балла. Эти задания сопровождаются большими расчетами, поэтому на первое место надо ставить внимательность их выполнения.
Необходимо выделить следующие моменты в решении:
- определять работу графически можно только в координатах рV;
- если в условии дан график в других координатах, то его надо перечертить в рV;
- поэтапно применять первый закон термодинамики и газовые законы для всех процессов;
Читайте также: