Как рассчитывается момент инерции диска
В нашем обиходе довольно часто встречаются выражения « он совершенно инертный» или «его инертность заставляет задуматься». Их применяют в отношении человека, который не обладает инициативой и не привык двигаться. Существуют другие понятия такого лица, но думаю, что они больше относятся к медицине. В общем понимании это человек не любящий принимать собственных решений. Или возьмем пример из цирка, где силач под аплодисменты зрителей выдерживает валун огромной массы. Данный объект лежит совершенно спокойно и не совершает никаких движений. Напарник бьет по камню и атлету совершенно не больно. Вся причина кроется в том, что объект инертен по отношению к цирковому артисту. Если бы на месте огромного валуна был маленький камушек, был бы тот же эффект.
Также можем применить пример из жизни, когда пешеход стоит на проезжей части и наблюдает за несущимся автомобильным потоком. Тяжелогруженная машина, если решила совершить остановку начинает тормозить раньше, чем легковая и совершает движение по инерции под влиянием груза. Естественно, что грузовик продвинется гораздо дальше по сравнению с легковушкой.
Что такое инерция
В научном понимании это свойство тел находится в состоянии покоя, при этом внешние силы никакого воздействия не осуществляют. Понятие момента инерции вызывает определенный вопрос. Не каждому обывателю понятно это выражение, поэтому разберем его подробнее. Инерция, это свойство отдельного тела, лежать в спокойном состоянии при отсутствии на него внешних действий различной силы. Также объект может воспрепятствовать изменчивости скоростных показателей. Из жизни мы можем привести такой пример, когда машина находится на льду и начинает тормозить, то она не сразу останавливается, а совершает поступательное движение благодаря льду. Весь тормозной путь будет считаться инерцией. Или размешивая чай в стакане после того, как перестанем мешать, жидкость продолжает совершать вращательное движение. Это будет считаться инерцией.
Определение момента инерции
Еще со школьной скамьи нам было известно, что масса, это масса инертности тела. Если к примеру, мы совершим толчок двух вагонов у которых разный вес, то совершенно понятно, что остановить труднее будет тот вагон, у которого масса тяжелее. Одним словом, чем больше вес, тем нужно большее усилие для совершения движения. В данной ситуации мы рассматриваем поступательное движение, когда вагон совершает движение прямо.
Высчитывают момент инертности при помощи следующей формулы.
Применяется она обычно в научной физике, при вычислении момента инерции тела. Если представить объект, разбившийся на несколько кусков, то момент инерции будет равняться сумме этих кусков, умноженный на квадрат расстояния к оси вращения. Так определяют момент инерции в физике. Если брать реальность, то определение происходит в результате расчетов, произведенных по формуле Штейнера.
Теорема Штейнера
Прежде всего, нам нужно понять, отчего зависит момент инерции. Ответ достаточно прост: от веса, оси вращения, формы и габаритов объекта. Теорема Штейнера имеет важное значение и студенты часто ее используют для решения различных задач. Что же она обозначает? Она имеет следующую формулировку. Момент инерции объекта относительно оси равен сумме момента инерции тела относительно оси, которая проходит через центр параллельно оси и произведения массы тела на квадрат расстояния между осями.
Немного мудреное понятие, но именно так объясняется теорема. В физике существуют разнообразные виды инерции: например, центральный или геометрический. Момент инерции является единицей измерения для тела, которое совершает вращательное движение вокруг своей оси.
Пример решения задачи
Вашему вниманию представим 2 варианта. В первом случае мы попытаемся найти момент инерции, а во втором, применим знания полученные при изучении теоремы Штейнера.
Упражнение 1. Установить момент инерции диска весом М и радиусом Р. Ось вращения соответственно расположена по центру объекта.
Оптимальное решение:
Диск делится на маленькие колечки, радиус которых изменяется от 0 до Р. Разберем более подробно отдельное кольцо. Обозначим, что его вес равен значение м, а радиус показателю р. Тогда получим момент инерции равный: DJ= DMR в квадрате.

Определение момента инерции
Со школьной программы по физике мы прекрасно знаем, что масса тела является мерой его инертности. Например, если в супермаркете сильно толкнуть две тележки, одна из которых будет пустой, а вторая нагруженной разными товарами, то впоследствии остановить будет труднее тележку, нагруженную товарами в силу ее большей массы. Другими словами, чем больше у тела масса, тем большее на него воздействие инерции и тем больше нужно сил, чтобы изменить движение такого тяжелого тела.
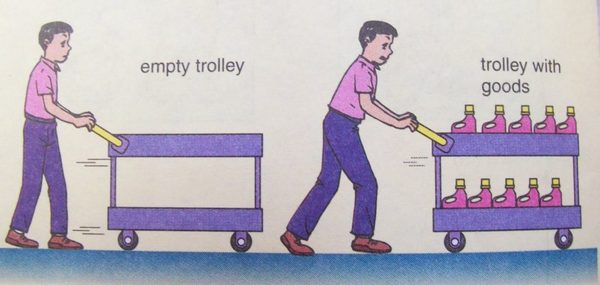
В приведенном примере тележка движется по прямой линии, то есть иными словами совершает поступательное движение. И если при поступательном движении какого-либо теле его масса является мерой его инерции, то при вращательном движении тела вокруг своей оси мерой его инерции будет величина, которая собственно и называется – момент инерции.
Момент инерции – скалярная физическая величина, мера инертности тела при его вращении вокруг оси. Обычно обозначается буквой J и измеряется в килограммах, умноженных на квадратный метр. Такое академическое определение того, что такое момент инерции.
Формула момента инерции
Как рассчитать точное значение момента инерции? Для этого есть общая формула, помогающая физикам определять момент инерции любого тела. Если тело разбить на бесконечно маленькие кусочки с массой dm, то момент инерции будет равным сумме произведения этих элементарных масс на квадрат расстояния до оси вращения. Формула будет иметь такой вид:
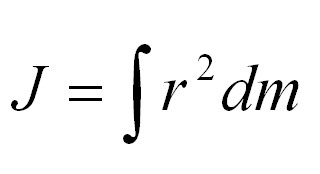
J – момент инерции, r – расстояние до оси вращения.
Для материальной точки массы m, которая вращается вокруг оси на расстоянии r, данная формула будет иметь такой вид:
Теорема Гюйгенса – Штейнера
Говоря о моменте инерции невозможно не упомянуть о теореме двух математиков Гюйгенсе и Штейнере, которые дали формулировку определению характеристики параллельных осей.
Теорема Гюйгенса – Штейнера гласит: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Если записать вышесказанное математической формулой, то получится следующее:
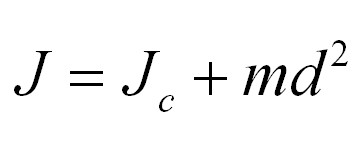
Где d – расстояние между осями
Эта теорема значительно облегчает решения многих физических задач, связанных с инерцией. К примеру, у Вас имеется объект произвольной формы, центробежная сила которого известна. При помощи формулы Штейнера можно вычислить момент инерции тела относительно любой оси параллельной линии, которая проходит через середину фигуры.
Моменты инерции простейших объектов
Несмотря на внешнюю простоту, вычисление моментов инерции для разных предметов предполагает знание интегралов, этих важных инструментов высшей математики. Для упрощения задачи создана таблица с вычислениями инерции для простых геометрических фигур: круга, квадрата, цилиндра и т. д.

Так выглядят математические расчеты вычисления моментов инерции для круга и кольца.
Аналогичным образом будет рассчитываться момент инерции цилиндра.
Предлагаем вашему вниманию более детальную таблицу с формулами для расчета момента инерции для основных геометрических фигур: шара, сферы, диска, цилиндров, и т. д.
Момент инерции тела относительно оси вращения является мерой инертности вращающегося тела.Момент инерции тела, которое можно представить в виде совокупности дискретных частиц, относительно оси вращения равен:
где – масса i-ой материальной точки тела; – расстояние от материальной точки i до оси вращения. При рассмотрении твердого тела как сплошной среды с непрерывным распределением массы определение момента инерции заменяют следующим:
где – элемент массы тела; – плотность тела; – элементарный объем.
Момент инерции однородного диска
Рассмотрим, как находится момент инерции однородного диска, если его радиус равен R, а масса m. Ось вращения пусть проходит через центр инерции данного диска (точку О) и будет перпендикулярна его плоскости (рис.1).

Диск можно заменить совокупностью бесконечно тонких колец, радиусы которых изменяются от нуля до R. На рис.1 выделено одно из таких колец. Рассмотрим это кольцо. Радиус его обозначим как Момент инерции данного кольца (обозначим его равен (см. формулу момента инерции тонкого кольца):
Массу данного кольца (а точнее цилиндра) можно представить как:
где – высота цилиндра. Подставим выражение для в формулу (3) и проведем интегрирование:
где – масса диска.
Если диск можно считать абсолютно тонким или он является частью цилиндра, то формула для вычисления момента инерции диска относительно оси, проходящей через его центр масс, и перпендикулярной плоскости диска, имеет вид:
В случае плоского распределения масс выполняется равенство:
где оси вращения совпадают с осями декартово системы координат. И если мы будем считать, что ось Z проходит через центр инерции диска и перпендикулярна его плоскости, то моменты инерции относительно осе X и Y будут равны:
Иногда величины моментов инерции называют моментами инерции диска относительно его диаметров.
| Задание | Радиус однородного диска равен R, его масса m. Каков момент инерции диска относительно оси, которая проходит через середину одного из радиусов диска, перпендикулярно его плоскости? |
| Решение | Момент инерции диска относительно оси, проходящей через его центр масс, и перпендикулярной плоскости диска, имеет равен: |
Ось вокруг, которой происходит вращение нашего диска, параллельна основной, и сдвинута от нее на расстояние . Для такой ситуации подходит теорема Штейнера:
Подставим из (1.1) и учтем расстояние между осями, получим:

где ; – масса вырезанной части диска. Подставим выражение (2.3) в формулу (2.1), имеем:
Найдем соотношение между массой диска и массой части, которую вырезали.
Многие люди замечали: когда они едут в автобусе, и он увеличивает свою скорость, их тела прижимаются к креслу. И наоборот, при остановке транспортного средства пассажиров будто выбрасывает из посадочных мест. Все это происходит из-за инерции. Рассмотрим это явление, а также объясним, что такое момент инерции диска.
Что представляет собой инерция?
Под инерцией в физике понимают способность всех тел, обладающий массой, сохранять покоящееся состояние либо двигаться с одинаковой скоростью в одном и том же направлении. Если необходимо изменить механическое состояние тела, то приходится прикладывать некоторую внешнюю силу к нему.

Вам будет интересно: Особенности и отличия австралийского английского языка от британского
В данном определении следует обратить внимание на два момента:
- Во-первых, это вопрос состояния покоя. В общем случае такого состояния не существует в природе. Все в ней находится в постоянном движении. Тем не менее, когда мы едем в автобусе, то нам кажется, что водитель не двигается со своего места. В таком случае идет речь об относительности движения, то есть относительно пассажиров водитель находится в покое. Отличие между состояниями покоя и равномерного движения заключается лишь в системе отсчета. В примере выше пассажир в состоянии покоя относительно автобуса, в котором едет, но движется относительно остановки, которую проезжает.
- Во-вторых, инерция тела пропорциональна его массе. Наблюдаемые нами объекты в жизни все имеют ту или иную массу, поэтому все они характеризуются некоторой инертностью.

Таким образом, инерция характеризует степень трудности изменения состояния движения (покоя) тела.
Инерция. Галилей и Ньютон

Когда изучают вопрос инерции в физике, то как правило, связывают ее с первым ньютоновским законом. Этот закон гласит:
Любое тело, на которое не действуют внешние силы, сохраняет свое состояние покоя либо равномерного и прямолинейного движения.
Считается, что этот закон сформулировал Исаак Ньютон, и произошло это в середине XVII века. Отмеченный закон справедлив всегда и во всех процессах, описываемых классической механикой. Но когда ему приписывают фамилию английского ученого, следует сделать некоторую оговорку.
В 1632 году, то есть за несколько десятков лет до постулирования закона инерции Ньютоном, итальянский ученый Галилео Галилей в одной из своих работ, в которой он сравнивал системы мира Птолемея и Коперника, по сути сформулировал 1-й закон "Ньютона"!
Галилей говорит, что если тело движется по гладкой горизонтальной поверхности, и силами трения и сопротивления воздуха можно пренебречь, то это движение будет сохраняться вечно.
Вращательное движение
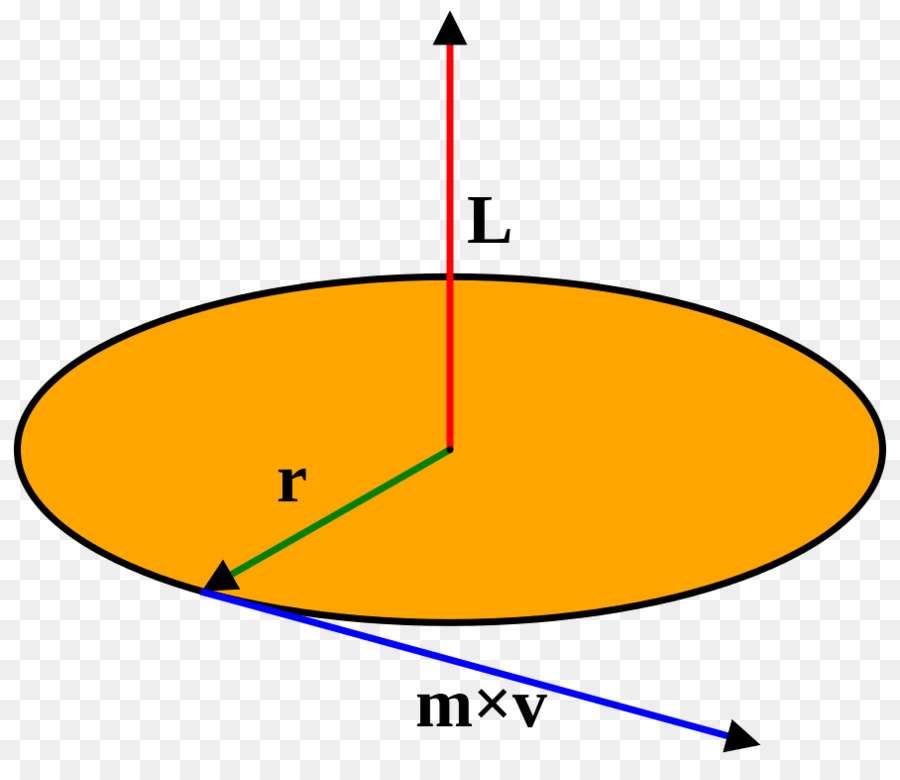
Приведенные выше примеры рассматривают явление инерции с точки зрения прямолинейного перемещения тела в пространстве. Однако существует еще один тип движения, который распространен в природе и Вселенной - это вращение вокруг точки или оси.
Масса тела характеризует его инерционные свойства поступательного движения. Для описания же аналогичного свойства, которое проявляет себя при вращении, вводят понятие момента инерции. Но перед тем как рассматривать эту характеристику, следует познакомиться с самим вращением.
Круговое перемещение тела вокруг оси или точки описывается двумя важными формулами. Ниже они приводятся:
В первой формуле L - это момент импульса, I - момент инерции, ω - угловая скорость. Во втором выражении α - это ускорение угловое, которое равно производной по времени от угловой скорости ω, M - момент силы системы. Он рассчитывается как произведение результирующей внешней силы на плечо, к которому она приложена.
Первая формула описывает вращательное движение, вторая - его изменение во времени. Как видно, в обеих этих формулах присутствует момент инерции I.
Момент инерции
Сначала приведем его математическую формулировку, а затем объясним физический смысл.
Итак, момент инерции I рассчитывается следующим образом:
Если перевести это выражение с математического на русский язык, то оно означает следующее: все тело, которое имеет некоторую ось вращения O, разбивается на мелкие "объемчики" массой mi, находящиеся на расстоянии ri от оси O. Момент инерции рассчитывается путем возведения в квадрат этого расстояния, его умножения на соответствующую массу mi и сложения всех полученных слагаемых.
Если разбить все тело на бесконечно малые "объемчики", тогда сумма выше будет стремиться к следующему интегралу по объему тела:
I = ∫V(ρ *r2dV), где ρ - плотность вещества тела.
Из приведенного математического определения следует, что момент инерции I зависит от трех важных параметров:
- от значения массы тела;
- от распределения массы в теле;
- от положения оси вращения.
Физический смысл момента инерции заключается в том, что он характеризует, насколько "тяжело" привести в движение вращения данную систему или изменить ее скорость вращения.
Момент инерции диска однородного

Полученные в предыдущем пункте знания применимы для расчета момента инерции однородного цилиндра, который в случае h Понравилась статья? Поделись с друзьями:

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Читайте также:

