Как определить радиус качения колеса
Данный пост посвящён рациональному выбору ряда КПП и размера шин для достижения максимально возможной скорости на примере ЛГЛ со штатным мотором и фильтром нулевого сопротивления.
Справочная информация
Штатная КПП Лады имеет следующие передаточные числа:
● ГП n0 = 63/17 = 3.706 или = 63/16 = 3.938 (на АМТ 1.0 только 3.7, на АМТ 2.0 поставили 3.9, на МКПП бывает 3.9)
● передачи n1 = 40/11 = 3.636, n2 = 39/20 = 1.950, n3 = 38/28 = 1.357, n4 = 32/34 = 0.941, n5 = 29/37 = 0.784
1. Взаимосвязь скорости автомобиля и частоты вращения коленвала
Тут всё просто, и я уверен, что многим хорошо известно. Приведу это в качестве напоминания.
Скорость v автомобиля вычисляется по формуле:
v = ω∙R/(n0∙ni), (1)
где
v — скорость, м/c;
ω — круговая частота вращения коленвала, рад/с;
R — эффективный радиус качения колеса, м;
n0 — ГП, ni — i-ая передача.
Что такое радиус качения колеса и чем он отличается от внешнего радиуса R0 шины?
Допустим, шины имеют размер 195/55-15" (у моих шин именно такой размер). Тогда внешний радиус шины можно приблизительно вычислить по формуле:
R0 = 195мм∙55%+15"/2 = 297.75 мм.
Почему приблизительно?
Да потому, что профиль шины не абсолютно точно равен 55% её ширины. Имеется определённый допуск, а отклонение может составлять 1%. Например, Nankang NS-2 и Toyo CF2 имеют R0 = 297.5 мм, что почти не отличается от теоретического значения, а вот у Toyo T1-R R0 = 296.5 мм (хотя и тут различие относительно мало).
Почему мы не можем подставить R0 в формулу (1) для скорости?
Дело в том, что шина под нагрузкой деформируется. Общая деформация шины складывается из деформации боковины и деформации протектора. Это приводит к уменьшению её радиуса R качения.
Как определить радиус качения?
Всё просто, достаточно выразить R из формулы (1):
R = v∙n0∙ni/ω (2)
Пример 1.
Я провёл эксперимент и выяснил, что если ехать на 5-ой передаче и установить на круиз-контроле скорость v = 76 км/ч (по GPS), то обороты двигателя составят ω = 2020 об/мин (при этом давление в шинах 2.1 атм). Используя формулу (2), для моих достаточно подстёртых передних шин Continental CPC5 получаем:
R = 289.88 мм
Относительная разница с теоретическим значением составляет:
Это показательный пример, и полученной величиной δR можно пользоваться при практических расчётах.
2. Оценка максимально возможной скорости автомобиля
При больших скоростях движения технически исправного автомобиля с правильно накачанными шинами основная сила сопротивления является силой Fx лобового сопротивления. Она вычисляется по формуле:
Fx(v) = Cx∙½ρ∙v²∙S, (3)
где
Cx — безразмерный коэффициент лобового сопротивления,
ρ — плотность воздуха (зависит от температуры), кг/м³,
S — характерная площадь (площадь миделя), м².
Что происходит с автомобилем во время движения?
Двигатель совершает работу. Работа, совершаемая двигателем за единицу времени, характеризуется его мощностью N(ω), которая есть непостоянная величина и зависит от оборотов коленвала.
На что расходуется мощность двигателя?
С одной стороны, она идёт на увеличение кинетической энергии автомобиля. С другой стороны, часть мощности расходуется на преодоление сил сопротивления. Как известно, мощность — это произведение силы на скорость, поэтому мощность сил лобового сопротивления вычисляется по формуле:
N(Fx(v)) = Cx∙½ρ∙v³∙S (4)
Здесь самое важное, что мощность сил лобового сопротивления пропорциональна кубу (!) скорости:
До каких пор автомобиль может разгоняться?
До тех пор, пока мощность двигателя не сравняется с мощностью всех сил сопротивления, ведь в этом случае у мотора не остаётся резервов для изменения кинетической энергии автомобиля, т.е. для изменения его скорости.
Пример 2.
Ещё один эксперимент, который я провёл, заключался в определении максимальной скорости моего автомобиля (у меня мотор штатный, кроме ФНС). Её величина составила V = 201 км/ч.
Что мы можем из этого выяснить?
Во-первых, при этой скорости достигается баланс мощностей:
N(ω) = N(Fx(V))
Во-вторых, этот баланс достигается на оборотах:
ω = V∙n0∙n5/R = 5340 об/мин (6)
Есть ли у мотора резервы для увеличения максимальной скорости?
Да, есть, ведь максимальная мощность моторов 21127 и 21129 достигается при частоте ωmax = 5800 об/мин.
На сколько можно увеличить максимальную скорость?
Чтобы это вычислить, нужно, используя (5), составить пропорцию:
N(ωmax)/N(ω) = N(Fx(Vmax))/N(Fx(V)) = (Vmax/V)³ (7)
Из ПТС известно, что максимальная мощность Гранты составляет N(ωmax) = 78 кВт. Судя по ВСХ моторов 21127 и 21129 их мощность при частоте ω = 5340 об/мин составляет N(ω) = 73 кВт. Конечно, это приблизительная величина, для более точных значений можно было бы воспользоваться каким-нибудь Android-приложением измерения мощности автомобиля (например, Torque или PerfExpert). При этом надо пользоваться не абсолютными значениями мощности, а составлять пропорцию подобно (7).
В результате можно сказать, что для ЛГЛ со штатным мотором максимально достижимая скорость равна:
Vmax = V∙³√N(ωmax)/N(ω) = 201∙³√78/73 = 205 км/ч (8)
3. Подбор ряда КПП и размера шин
Задача состоит в том, чтобы при частоте коленвала ωmax = 5800 об/мин скорость автомобиля составляла Vmax = 205 км/ч.
Снова преобразуем формулу (1):
R/(n0∙n5) = v/ω (9)
и введём обозначение
r = R/(n0∙n5) (10)
В случае максимальной скорости:
rmax = Vmax/ωmax = 94 мм (11)
На текущих шинах и КПП это значение равно:
что очень много, т.е. мы имеем "длинную" трансмиссию и "высокие" шины.
Что будет, если уменьшить размер шин, не меняя при этом ряд КПП?
Изменим только профиль шин на более низкий, т.е. возьмём шины 195/50-15". Вычислим их радиус качения с учётом поправки δR:
R = R0∙(1−δR) = (195мм∙50%+15"/2)∙(1−2.6%) = 280.39 мм
Тогда на штатной КПП
т.е. мы стали ближе к rmax, а, следовательно, максимальная скорость стала ближе к максимально достижимой скорости.
Что будет, если изменить ряд КПП, не меняя при этом размера шин?
Заменим только ГП с 3.7 на более короткую 3.9. Тогда на текущих высоких шинах 195/55-15" получим
При качении шина подвергается действию центробежных сил. Величина центробежных сил зависит от скорости качения, массы и размеров шины. Под действием центробежных сит шина несколько увеличивается по диаметру. Испытания показали, что при качении шины со скоростью 180—220 км/ч высота профиля увеличивается на 10—13% (результаты испытаний шин на шоссейно-кольцевых мотоциклетных гонках).
Одновременно действие центробежных сил вызывает (за счет увеличения радиальной жесткости шины) некоторое увеличение расстояния от оси колеса до опорной поверхности (плоскости дороги) с одновременным уменьшением площади контакта шины с дорогой. Это расстояние называется динамическим радиусом шины Rо, который больше, чем статический радиус Rс, т. е. Rо>Rc.
Однако при эксплуатационных скоростях движения Rо, практически равен Rс.
Радиусом качения называется отношение линейной скорости движения колеса к угловой скорости вращения колеса:
Rк = V/w
где Rк — радиус качения, м;
V — линейная скорость, м/с;
w — угловая скорость, рад/с.
Сопротивление качению
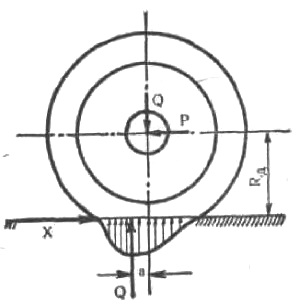
Рис. Качение шины по твердой поверхности
При качении колеса по твердой поверхности каркас шины подвержен циклическим деформациям. При входе в контакт шина деформируется и прогибается, а при выходе из контакта — восстанавливает свою первоначальную форму. Энергия деформации шины, образующаяся при входе элементов в контакт с поверхностью, расходуется на внутреннее трение между слоями каркаса и проскальзывание в зоне контакта. Часть этой энергии превращается в тепло и передается окружающей среде. Вследствие потерь механической энергии скорость восстановления первоначальной формы шины при выходе элементов шины из контакта меньше скорости деформации шины при входе элементов в контакт. В силу этого нормальные реакции в зоне контакта несколько перераспределяются (по сравнению с неподвижным колесом) и эпюра распределения нормальных сил принимает вид, как показано на рисунке. Равнодействующая нормальных реакций, равная по величине радиальной нагрузке на шину, перемещается вперед по отношению к вертикали, прохооящей через ось колеса, на некоторую величину а («снос» радиальной реакции).
Момент, создаваемый радиальной реакцией относительно оси колеса, называется моментом сопротивления качению:
При условии установившегося движения (при постоянной скорости качения) ведомого колеса действует момент, уравновешивающий момент сопротивления качению. Этот момент создается двумя силами — толкающей
силой Р и горизонтальной реакцией дороги X:
М = XRд = PRд,
где Р — толкающая сила;
X — горизонтальная реакция дороги;
Rд — динамический радиус.
PRд = Qa — условие установившегося движения.
Отношение толкаюшей силы Р к радиальной реакции Q называется коэффициентом сопротивления качению k.
На коэффициент сопротивления качению кроме шины значительное влияние оказывает качество дорожного покрытия.
Мощность Nк, затрачиваемая на качение ведомого колеса, равна произведению силы сопротивления качению Рс на линейную скорость качения V:
Раскрывая это уравнение, можно написать:
Nк = N1 + N2 + N3 — N4,
где N1 — мощность, затрачиваемая на деформацию шины;
N2 — мощность, затрачиваемая на проскальзывание шины в зоне контакта;
N3 — мощность, затрачиваемая на трение в подшипниках колеса и сопротивление воздуха;
N4— мощность, развиваемая шиной при восстановлении формы шины в момент выхода элементов из контакта.
Потери мощности на качение колеса значительно возрастают с увеличением скорости качения, так как в этом случае возрастает энергия деформации и, следовательно, большая часть энергии превращается в тепло.
При увеличении прогиба резко возрастает деформация каркаса и протектора шины, т. е. потери энергии на гистерезис.
Одновременно увеличивается теплообразование. Все это, в конечном итоге, ведет к увеличению мощности, затрачиваемой на качение шины.
Испытания показали, что на качение мотоциклетной шины в условиях ведомого колеса (по гладкому барабану) затрачивается мощность от 1,2 до 3 л. с. (в зависимости от размера шины и скорости качения).
Таким образом, общие потери от шин весьма значительны и соизмеримы с мощностью двигателя мотоцикла.
Совершенно очевидно, что решение вопроса снижения мощности, затрачиваемой на качение мотоциклетных шин, имеет исключительное значение. Уменьшение этих потерь не только увеличит долговечность шин, но значительно увеличит моторесурс двигателя и агрегатов мотоцикла, а также положительно скажется на топливной экономичности двигателей.
Исследования, проведенные при создании шин типа Р, показали, что потери мощности при качении шин этого типа значительно меньше (на 30—40%), чем у шин стандартной конструкции.
Кроме того, снижаются потери при переводе шин на двухслойный каркас из корда 232 КТ.
Особенно важно максимально снизить потери мощности при качении шин для гоночных мотоциклов, так как при их движении на высоких скоростях потери в шинах составляют до 30% по отношению к общим затратам мощности на движение. Один из методов снижения этих потерь — применение в каркасе гоночных шин капронового корда 0,40 К. Применив такой корд, уменьшили толщину каркаса, снизили вес шины, она стала более эластичной, менее подверженной нагреву.
Большое влияние на коэффициент сопротивления качению шины оказывает характер рисунка протектора.
Для уменьшения энергии, образующейся при входе элементов в контакт с дорогой, максимально снижена масса протектора гоночных шин. Если у дорожных шин глубина рисунка протектора находится в пределах 7—9 мм, то у гоночных шин она составляет 5 мм.
Кроме того, рисунок протектора гоночных шин выполняют таким образом, чтобы его элементы оказывали наименьшее сопротивление при качении шины.
Как правило, рисунок протектора шин переднего (ведомого) и заднего (ведущего) колес мотоцикла различен. Это объясняется тем, что назначение шины переднего колеса — обеспечение надежной управляемости, а заднего колеса — передача крутящего момента.
Наличие кольцевых выступов на шинах передних колес способствует снижению потерь при качении и улучшает управляемость и устойчивость, особенно на поворотах.
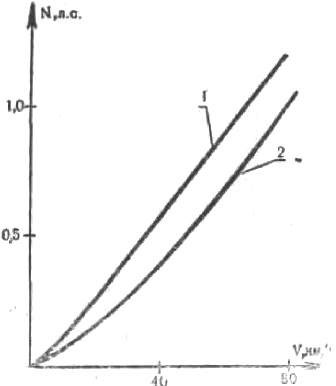
Рис. Кривые зависимости потерь мощности от скорости качения: 1 — шина размера 80-484 (3,25-19), модели Л-130 (дорожная); 2 — шина размера 85-484 (3,25-19) модели Л-179 (для заднего колеса шоссейно-кольцевых мотоциклов)
Зигзагообразный рисунок протектора заднего колеса обеспечивает надежную передачу крутящего момента и также снижает потери на качение. Все вышеизложенные меры позволяют в общем существенно снизить потери мощности при качении шин. На графике показаны кривые изменения потерь мощности при различных скоростях для дорожных и гоночных шин. Как видно из рисунка, гоночные шины по сравнению с дорожными имеют меньшие потери.
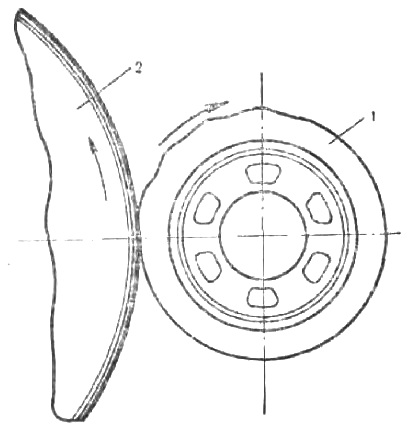
Рис. Появление «волны» при качении шины на критической скорости: 1 — шина; 2 — барабан испытательного стенда
Критическая скорость качения шины
Когда скорость качения шины достигает некоторого предельного значения, потери мощности на качение резко возрастают. Коэффициент сопротивления качению увеличивается примерно в 10 раз.
На поверхности беговой дорожки шины появляется «волна». Эта «волна», оставаясь неподвижной в пространстве, перемещается по каркасу шины со скоростью ее вращения.
Образование «волны» приводит к быстрому разрушению шины. В зоне протектора-каркаса резко увеличивается температура, так как внутреннее трение в шине становится более интенсивным, и уменьшается прочность связи между протектором и каркасом.
Под действием центробежных сил, значительных по величине при высоких скоростях качения, происходит отрыв участков протектора или элементов рисунка.
Скорость качения, при которой появляется «волна», считается критической скоростью качения шины.
Как правило, при качении на критической скорости шина разрушается после пробега 5—15 км.
При увеличении давления в шине критическая скорость увеличивается.
Однако практика показывает, что во время ШКХ скорость движения мотоциклов на некоторых участках на 20—25% превышает критическую скорость шин, определенную на стенде (при качении шины по барабану). При этом шины не разрушаются. Это объясняется тем, что при качении по плоскости деформация шины меньше (при одинаковом режиме), чем при качении по барабану, а следовательно, критическая скорость выше. Кроме того время движения мотоцикла со скоростью, превышающей критическую скорость шин, незначительно. При этом шина хорошо охлаждается встречным потоком воздуха. В связи с этим технические характеристики шин спортивных мотоциклов, предназначенных для ШКГ, допускают кратковременное превышение скорости в определенных пределах.
Качение шины в условиях ведущего и тормозного колеса. Качение шины в условиях ведущего колеса происходит при приложении к колесу крутящего момента Мкр.
Схема сил, действующих на ведущее колесо, приведена на рисунке.
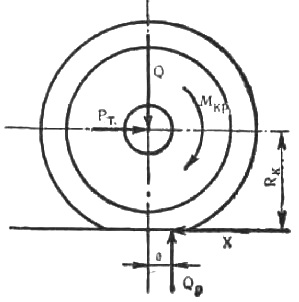
Рис. Схема сил, действующих на шину ведущего колеса при качении
К колесу, нагруженному вертикальной силой Q, приложен крутящий момент Мкр.
Реакция дороги Qp, равная по величине нагрузке Q, смещена относительно оси колеса на некоторое расстояние а. Сила Qp создает момент сопротивления качению Мс:
Крутящий момент Мкр создает тяговую ситу Рт:
При качении шины в условиях ведущего колеса под действием крутящего момента происходит перераспределение касательных сил в контакте.
В передней по направлению движения части контакта касательные силы увеличиваются, в задней — уменьшаются. При этом равнодействующая касательных сил X равна тяговой силе Рт.
Мощность, затрачиваемая на качение ведущего колеса, равна произведению крутящего момента Мкр на угловую скорость Wк вращения колеса:
Это уравнение справедливо только в том случае, когда в контакте отсутствует проскальзывание.
Однако касательные силы вызывают проскальзывание элементов рисунка протектора относительно дороги.
В силу этого действительная величина скорости поступательного движения колеса Уд несколько ниже теоретической Vт.
Отношение действительной скорости поступательного движения Vд к теоретической Vт называется коэффициентом полезного действия колеса, учитывающим потери скорости на проскальзывание шины относительно дороги.
Величину проскальзывания а можно оценить по следующей формуле:
Очевидно, значение действительной скорости Vд может меняться в пределах от Vт до 0, т. е.:
Интенсивность проскальзывания зависит от величины касательных сил, определяемых в свою очередь величиной крутящего момента.
Ранее было показано:
Mкр = XRк;
Х = Рт = Qv,
где v — коэффициент сцепления шины с дорогой.
При увеличении крутящего момента до некоторого значения, превышающего критическое, величина равнодействующей касательных сил X становится выше допустимой и шина полностью проскальзывает относительно дороги.
Cуществующие мотоциклетные шины в диапазоне рабочих нагрузок могут передавать без полного проскальзывания крутящий момент 55—75 кгс*м (в зависимости от размера шины, величины нагрузки, давления и т. д.).
При торможении мотоцикла силы, действующие на шину, по характеру аналогичны силам, возникающим при работе шины в условиях ведущего колеса.
При приложении к колесу тормозного момента Мт в зоне контакта происходит перераспределение касательных сил. Наибольшие касательные силы возникают в задней части контакта. Равнодействующая касательных сил по величине и направлению совпадает с тормозной силой Т:
При увеличении тормозного момента Мт выше некоторого критического значения тормозная сила Т становится больше силы сцепления шины с дорогой (T>Qv) и в контакте начинается полное проскальзывание, наступает явление юза.
При торможении на юз в зоне контакта повышается температура протектора, падает коэффициент сцепления, резко увеличивается износ рисунка протектора. Эффективность торможения уменьшается (увеличивается тормозной путь).
Наиболее эффективное торможение происходит при значениях тормозной силы Т, близкой по величине силе сцепления шины с дорогой.
Следовательно, при использовании водителем динамических качеств мотоцикла в целях уменьшения износа шин к ведущему колесу должен подводиться крутящий момент, обеспечивающий наименьшее проскальзывание шины относительно дороги.
Автомобиль (трактор) движется в результате действия на него различных сил, которые делятся на движущие силы и силы сопротивления движению. Основной движущей силой является тяговая сила, приложенная к ведущим колесам. Тяговая сила возникает в результате работы двигателя и вызвана взаимодействием ведущих колес с дорогой. Тяговую силу Pк определяют как отношение момента на полуосях к радиусу ведущих колес при равномерном движении автомобиля. Следовательно, для определения тяговой силы необходимо знать величину радиуса ведущего колеса. Поскольку на колеса автомобиля устанавливаются эластичные пневматические шины, то величина радиуса колеса во время движения изменяется. В связи с этим различают следующие радиусы колес:
1.Номинальный – радиус колеса в свободном состоянии: rн=d/2+H, (6)
где d – диаметр обода, м;
H – полная высота профиля шины, м.
2.Статический rс – расстояние от поверхности дороги до оси нагруженного неподвижного колеса.
3.Динамический rд–расстояние от поверхности дороги до оси катящегося нагру женного колеса. Этот радиус увеличивается с уменьшением воспринимаемой нагрузки колесом Gк и увеличением внутреннего давления воздуха в шине pш.
При увеличении скорости автомобиля под действием центробежных сил шина растягивается в радиальном направлении, вследствие чего радиус rд увеличивается. При качении колеса изменяется и деформация поверхности качения в сравнении с неподвижным колесом. Поэтому плечо приложения равнодействующих касательных реакций дороги rд отличается от rс. Однако, как показали эксперименты, для практических тяговых расчетов можно принимать rс
4 Кинематический радиус (качения) колеса rк – радиус такого условного недеформирующегося кольца, которое имеет с данным эластичным колесом одинаковую угловую и линейную скорости.
У колеса, катящегося под действием крутящего момента, элементы протектора, входящие в контакт с дорогой, сжаты, и колесо при равных частотах вращения проходит меньший путь, чем во время свободного качения; у колеса же, нагруженного тормозным моментом элементы протектора, входящие в контакт с дорогой, растянуты. Поэтому тормозное колесо проходит при равных числах оборотов несколько больший путь, чем свободно катящееся колесо. Таким образом, под действием крутящего момента радиус rк – уменьшается, а под действием тормозного момента – увеличивается. Для определения величины rк методом “меловых отпечатков” на дороге мелом или краской наносят поперечную линию, на которую накатывается колесо автомобиля, а затем оставляет на дороге отпечатки.
где n – частота вращения колеса, соответ ствующая расстоянию l .
В случае полного буксования колеса расстояние l = 0 и радиус rк = 0. Во время скольжения невращающихся колес (“ЮЗ”) частота вращения n=0 и rк .
В связи с большим многообразием видов деформации пневматической шины ее радиус не имеет одного определенного значения, как у колеса с жестким ободом.
Различают следующие радиусы качения колеса с пневматической шиной: свободный г0, статический rcv динамический га и кинематический гк.
Свободный радиус г0 — это наибольший радиус беговой дорожки колеса, свободного от внешней нагрузки. Он равен расстоянию от поверхности беговой дорожки до оси колеса.
Статический радиус гст представляет собой расстояние от оси неподвижного колеса, нагруженного нормальной нагрузкой, до плоскости его опоры. Значения статического радиуса при максимальной нагрузке регламентированы стандартом для каждой шины.
Динамический радиус гя — это расстояние от оси движущегося колеса до точки приложения результирующей элементарных реакций почвы, действующих на колесо.
Статический и динамический радиусы уменьшаются с увеличением нормальной нагрузки и с уменьшением давления воздуха в шине. Зависимость динамического радиуса от нагрузки моментом, полученная экспериментально Е.А. Чудаковым, показана на рис. 9, а, график 1. Из рисунка видно, что с увеличением момента Мвеа, передаваемого колесом, его динамический радиус уменьшается. Это объясняется тем, что расстояние по вертикали между осью колеса и его опорной поверхностью уменьшается вследствие деформации скручивания боковины шины. Кроме того, под действием крутящего момента возникает не только касательная сила, но и нормальная составляющая, которая стремится прижать колесо к поверхности дороги. 
Рис. 9. Зависимости, полученные Е.А. Чудаковым: а — изменение динамического (Я и кинематического (2) радиусов колеса в зависимости от ведущего момента: б — изменение кинематического радиуса колеса под действием ведущего и тормозного моментов
Величина динамического радиуса зависит также от глубины колеи при движении по деформируемому грунту или почве. Чем больше глубина колеи, тем меньше динамический радиус. Динамический радиус колеса является плечом приложения касательной реакции почвы, толкающей ведущее колесо. Поэтому динамический радиус называют еще силовым.
Кинематический радиус или радиус качения колеса — это поделенный на 2к действительный путь колеса пройденный за один оборот. Еще кинематический радиус определяют как радиус такого фиктивного колеса с жестким ободом, которое при отсутствии пробуксовывания и проскальзывания имеет одинаковую с действительным колесом угловую скорость вращения и поступательную скорость:
где vK — поступательная скорость качения колеса; сок — угловая скорость вращения колеса; SK — путь колеса за один оборот с учетом буксования или скольжения.
Из выражения (5) следует, что при полном буксовании колеса (vK = 0) радиус гк = 0, а при полном скольжении (сок = 0) кинематический радиус равен ©о.
На рис. 9, а (график 2) представлена полученная Е.А. Чудаковым зависимость изменения кинематического радиуса колеса от действия на него крутящего момента Мвед. Из рисунка следует, что величина изменения динамического и кинематического радиусов в зависимости от действия момента разная. Более крутая зависимость кинематического радиуса колеса по сравнению с зависимостью динамического радиуса может быть объяснена действием на него двух факторов. Во-первых, кинематический радиус уменьшается на ту же величину, на которую уменьшается динамический радиус от действия ведущего момента, как показано на рис. 9, я, график /. Во-вторых, приложенный к шине ведущий или тормозной момент вызывает деформацию сжатия или растяжения набегающей части шины. Сопровождающие эти деформации процессы легко проследить, если представить колесо в виде цилиндрической упругой спирали с равномерной навивкой витков. Как показано на рис. 10, а, под действием ведущего момента набегающая часть шины (передней) сжимается, вследствие чего общий периметр окружности протектора шины уменьшается, путь колеса SK за один оборот становится меньше. Чем больше деформация сжатия шины в набегающей части, тем больше снижение пути SK, что в соответствии с (5) пропорционально уменьшению кинематического радиуса гк.
При действии тормозного момента происходит обратное явление. К опорной поверхности подходят растянутые элементы шины
(рис. 10, б). Периметр шины и путь колеса SK, проходимый за один его оборот, возрастают по мере увеличения тормозного момента. Поэтому кинематический радиус увеличивается.

Рис. 10. Схема деформации шины от действия моментов Мвед (а) и Мт (б)
На рис. 9, б показана зависимость изменения радиуса колеса от действия на него крутящего активного Л/вед и тормозного М1 моментов при устойчивом сцеплении колеса с опорной поверхностью. Е.А. Чудаков предложил следующую формулу для определения радиуса колеса:
где гк 0 — радиус качения колеса при свободном режиме качения, когда ведущий момент и момент сопротивления качению равны между собой; А,т — коэффициент тангенциальной эластичности шины, зависящий от ее типа и конструкции, который находят по результатам экспериментов.
При инженерных расчетах в качестве динамического и кинематического радиусов обычно используют приведенный в стандарте статический радиус данной шины при установленном давлении воздуха и максимальной нагрузке на нее. Принимают, что колесо движется по несминаемой поверхности.
При движении по колее статический радиус — это расстояние от оси колеса до дна колеи. Однако при движении колеса по колее точка приложения равнодействующей элементарных реакций почвы, образовывающая крутящий момент (ведущий или сопротивления), будет находиться выше дна колеи и ниже поверхности почвы (см. рис. 17). Динамический радиус в этом случае зависит от глубины колеи: чем она глубже, тем больше разница между статическим и динамическим радиусами колес, тем больше погрешность расчетов от допущения гл = гст
Для подбора шин и определения по их размерам радиусов качения колеса необходимо знать распределение нагрузки по мостам.
У легковых автомобилей распределение нагрузки от полной массы по мостам зависит в основном от компоновки. При классической компоновке на задний мост приходится 52…55% нагрузки от полной массы, для переднеприводных автомобилей 48%.
Радиус качения колеса rк выбирается в зависимости от нагрузки на одно колесо. Наибольшая нагрузка на колесо определяется положением центра масс автомобиля, которое устанавливается по предварительному эскизу или прототипу автомобиля.
Следовательно, нагрузку на каждое колесо передней и задней оси автомобиля соответственно можно определить по формулам:
где G1, G2 - нагрузки от полной массы на переднюю и заднюю ось автомобиля соответственно.
Расстояние от передней оси до центра масс найдем по формуле:
где Ga – модуль сил тяжести автомобиля (Н);
L – база автомобиля.
Расстояние от центра масс до задней оси
Выбираем шины исходя из нагрузки на каждое колесо по Таблице 1.
Таблица 1 – Шины автомобилей
| Обозначение шины | Максимальная нагрузка, Н | Обозначение шины | Максимальная нагрузка, Н |
| 155-13/6,45-13 | 240-508 (8,15-20) | ||
| 165-13/6,45-13 | 260-508P (9,00P-20) | ||
| 5,90-13 | 280-508 (10,00-20) | ||
| 155/80 R13 | 300-508 (11,00R-20) | ||
| 155/82 R13 | 320-508 (12,00-20) | ||
| 175/70 R13 | 370-508 (14,00-20) | ||
| 175-13/6,95-13 | 430-610 (16,00-24) | ||
| 165/80 R13 | 500-610 (18,00-25) | ||
| 6,40-13 | 500-635 (18,00-25) | ||
| 185-14/7,35-14 | 570-711 (21,00-78) | ||
| 175-16/6,95-16 | 570-838 (21,00-33) | ||
| 205/70 R14 | 760-838 (27,00-33) | ||
| 6,50-16 | |||
| 8,40-15 | |||
| 185/80 R15 | |||
| 220-508P (7,50R-20) | |||
| 240-508 (8,25-20) | |||
| 240-381 (8,25-20) |
Например: 165-13/6,45-13 с максимальной нагрузкой 4250 Н, 165 и 6,45 - ширина профиля мм и дюймах соответственно, посадочный диаметр обода 13 дюймов. По этим размерам можно определить радиус колеса, находящегося в свободном состоянии
rc = + b, (10)
где b – ширина профиля шины (мм);
d – диаметр обода шины (мм), (1 дюйм = 25,4 мм)
Радиус качения колеса rк определяется с учетом деформации, зависящей от нагрузки
rк = 0,5 * d + (1 - k) * b, (11)
где k – коэффициент радиальной деформации. Для стандартных и широкопрофильных шин k принимают 0,1…0,16.
Расчет внешней характеристики двигателя
Расчет начинается с определения мощности Nev, необходимой для обеспечения движения с заданной максимальной скоростью Vmax.
При установившемся движении автомобиля мощность двигателя в зависимости от дорожных условий может быть выражена следующей формулой (кВт):
Nev = Vmax * (Ga * + Kв * F * V ) / (1000 * * Kp), (12)
где - коэффициент суммарного дорожного сопротивления для легковых автомобилей определяется по формуле:
=0,01+5*10 -6 * V . (13)
Kв – коэффициент обтекаемости, Kв = 0,3 Н*с 2* м -4 ;
F – лобовая площадь автомобиля, м 2 ;
- КПД трансмисии;
Kp – коэффициент коррекции.
Коэффициент суммарного дорожного сопротивления для грузовых автомобилей и автопоездов
=(0,015+0,02)+6*10 -6 * V . (14)
Лобовую площадь для легковых автомобилей находим из формулы:
где Bг – габаритная ширина;
Hг – габаритная высота.
Лобовая площадь для грузовых автомобилей
При рекомендуемых температурах масла в агрегатах механической трансмиссии = 0,8…0,95. Коэффициент коррекции в данном случае рекомендуется применять Kp =0,6…0,8.
Частота вращения коленчатого вала двигателя
Частота вращения коленчатого вала двигателя nv, соответствующая максимальной скорости автомобиля, определяется из уравнения (мин -1 ) :
nv = Vmax * , (17)
где - коэффициент оборотистости двигателя.
У существующих легковых автомобилей коэффициент оборотистости двигателя лежит в приделах 30…35, у грузовых с карбюраторным двигателем – 35…45; у грузовых с дизельным двигателем– 30…35.
Максимальная мощность двигателя
Максимальную мощность двигателя найдем из формулы:
Nmax = Nev / [ a * + b * ( ) 2 – c * ( ) 3 ] , (18)
где - отношение частоты вращения коленчатого вала двигателя при
максимальной скорости движения автомобиля к частоте
вращения при максимальной мощности двигателя;
a, b, c – коэффициенты, постоянные для каждого двигателя.
В случае упрощенного расчета можно применять для бензиновых двигателей a = b = c = 1; для дизелей с непосредственным впрыском а=0,5, в=1,5,с=1; для дизелей предкамерных а=0,8, в=1,4, с=1, для двухтактных дизелей а=0,87, в=1,13, с=1.
Для построения внешней характеристики при известной мощности Nmax и выбранных коэффициентах a, b, c , принимаем частоту вращения коленчатого вала при максимальной мощности от 5500 до 6500 мин -1 .
Читайте также:

