Как определить окружную скорость колеса
3.112 Окружная скорость - линейная окружная скорость шлифовального круга при работе.
Смотри также родственные термины:
3.5 окружная скорость v, м/с, и частота вращения n, мин -1 (rotational and peripheral speed):
Окружную скорость шлифовального круга вычисляют по формуле
где D - наружный диаметр шлифовального круга, мм;
частоту вращения шлифовального круга вычисляют по формуле
32. Окружная скорость концов лопастей несущего винта
Средняя окружная скорость концевой точки лопасти несущего винта при вращении при βл = ξл = 0.
Примечание. Среднюю окружную скорость рулевого винта обозначают ωpRр.в
Словарь-справочник терминов нормативно-технической документации . academic. 2015 .
Смотреть что такое "Окружная скорость" в других словарях:
окружная скорость — apskritiminis greitis statusas T sritis automatika atitikmenys: angl. circular velocity; circumferential speed; peripheral speed vok. Umfangsgeschwindigkeit, f rus. окружная скорость, f pranc. vitesse circulaire, f; vitesse périphérique, f … Automatikos terminų žodynas
окружная скорость (на периферии долота) — — [russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN peripheral velocity … Справочник технического переводчика
окружная скорость бурового долота — — [russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN circumferential drilling bit speedperipheral drilling bit speed … Справочник технического переводчика
окружная скорость конца лопасти — (напр. вентилятора, ветроэнергетической установки) [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN tip speed … Справочник технического переводчика
окружная скорость конца лопатки (турбины) — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN tip speed … Справочник технического переводчика

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.
При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.
2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности \( T \) — время, в течение которого тело совершает один полный оборот. Единица периода — \( [\,T\,] \) = 1 с.
Частота обращения \( (n) \) — число полных оборотов тела за одну секунду: \( n=N/t \) . Единица частоты обращения — \( [\,n\,] \) = 1 с -1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и периодом обращения выражается формулой: \( n=1/T \) .
Пусть некоторое тело, движущееся по окружности, за время \( t \) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол \( \varphi \) .

Быстроту обращения тела характеризуют угловая и линейная скорости.
Угловая скорость \( \omega \) — физическая величина, равная отношению угла поворота \( \varphi \) радиуса-вектора к промежутку времени, за которое этот поворот произошел: \( \omega=\varphi/t \) . Единица угловой скорости — радиан в секунду, т.е. \( [\,\omega\,] \) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен \( 2\pi \) . Поэтому \( \omega=2\pi/T \) .
Линейная скорость тела \( v \) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.
Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: \( \vec
Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.
4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: \( \vec=\frac<\Delta\vec
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. При равномерном движении тела по окружности
1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости
2. Линейная скорость точки 1, находящейся на расстоянии \( R_1 \) от центра вращающегося колеса, равна \( v_1 \) . Чему равна скорость \( v_2 \) точки 2, находящейся от центра на расстоянии \( R_2=4R_1 \) ?
1) \( v_2=v_1 \)
2) \( v_2=2v_1 \)
3) \( v_2=0,25v_1 \)
4) \( v_2=4v_1 \)
3. Период обращения точки по окружности можно вычислить по формуле:
1) \( T=2\pi\!Rv \)
2) \( T=2\pi\!R/v \)
3) \( T=2\pi v \)
4) \( T=2\pi/v \)
4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:
1) \( \omega=a^2R \)
2) \( \omega=vR^2 \)
3) \( \omega=vR \)
4) \( \omega=v/R \)
5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?
1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась
6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза
7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза
8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?
1) 200 000 с
2) 3300 с
3) 3·10 -4 с
4) 5·10 -6 с
9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?
1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц
10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?
1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с
11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения
ФОРМУЛА
1) \( 1/T \)
2) \( v^2/R \)
3) \( v/R \)
4) \( \omega R \)
5) \( 1/n \)
12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась
Часть 2
13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?
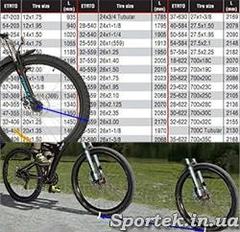
Для настройки велокомпьютера в него нужно внести длину окружности велосипедного колеса. Это основная настройка, в зависимости от которой рассчитывается большинство показателей.
Рассмотрим как ее найти.
Первый и самый простой способ найти длину окружности колеса велосипеда
Посмотреть на размер покрышки, написанный на ней сбоку, и выбрать в таблице к велокомпьютеру длину окружности колеса.
Обычно такие таблицы идут в комплекте с компьютером, но если ее нет, то приведем здесь один из вариантов.
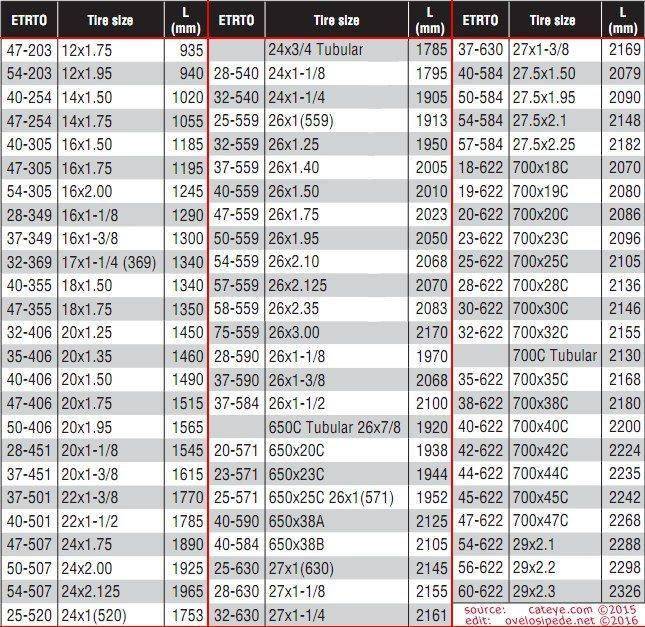
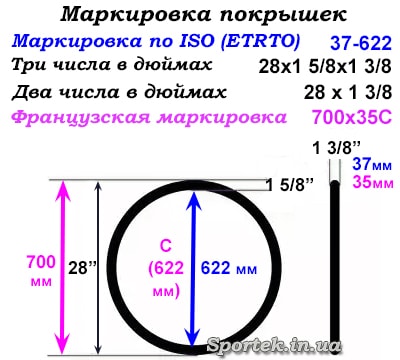
Уточнить совместимость разных маркировок и размеров покрышек можно в таблице взаимозаменяемости, а здесь приведем только схему с пояснениями какие цифры, что обозначают в различных видах маркировки размеров покрышек.
Второй способ измерить длину окружности колеса
Лучше всего его делать вдвоем – один сидит на велосипеде, а второй замеряет. При сидячем велосипедисте измерения будут более точными, так как учитывается сжатие покрышки при реальной поездке, да и ставить метки на асфальте удобнее. Не забудьте, что колеса должны быть накачены до того давления, на котором потом будите кататься.
- Ставим велосипед вертикально и хозяин садится на него.
- В месте соприкосновения колеса с дорогой мелом рисуем линию на боку покрышки и дороге. Они, естественно, должны совпадать.
- Проезжаем на велосипеде по прямой так, чтобы колесо сделало один полный оборот.
- Там где линия на колесе снова коснулась земли, ставим вторую метку.
- Измеряем расстояние между двумя метками – это и есть длина окружности колеса.
- Для повышения точности расчетов можно сделать 2-3 замера и взять среднее или проехать не один, а три оборота колеса и разделить полученное расстояние на 3.

Можно обмотать колесо швейным сантиметром, ниткой, бечевкой и измерить ее. Правда реальный опыт показывает, что это сделать менее удобно. Нитка должна лежать точно по верху покрышки, а не вилять по ее поверхности, что в теории легко, а на практике не очень. И, второе, при таком способе не учитывается прогиб покрышки.
Третий способ вычислить длину окружности колеса определив его радиус
Далее, для тех, кто помнит математику.
Измерить радиус колеса от центра втулки до наружного края покрышки (или до земли). Делать это нужно на стоящем велосипеде.
Лучше мерить вертикально до земли – так не будет погрешности на изгиб из-за того, что втулка значительно шире колеса.
Напоминаю - меряем именно от центра втулки, а не от ее краев, измеряя радиус покрышки по ее наружнему краю.
Точно измерив радиус колеса в мм и, вспомнив школьный курс математики, рассчитываем длину окружности по формуле: l = 2πR (или πD)
Длина окружности колеса (в мм) = 2 * 3,1415 (что есть число «Пи») * измеренный радиус (в мм)
Что можно получить дополнительно.
Через известный радиус, умножив его на 2, получаем диаметр покрышки в мм. Для перевода диаметра из мм в дюймы делим его на 25,4 (1 дюйм = 25,4 мм) и получаем размер колеса и его покрышки в дюймах. Результат вычислений можно округлить до стандартных дюймовых размеров колес, а длину окружности колеса выбрать из таблицы, приведенной в первом способе в начале статьи.
Когда-то, когда у меня была Subaru Impreza и я поменял штатные 14" колеса на 16", меня заинтересовал вопрос:
На сколько влияет смена колес на показатели приборов автомобиля?
При измерении скорости автомобиля, датчик скорости использует обороты колеса. В каждом автомобиле спидометр и датчик скорости настроены на штатный размер колес. Соответственно при смене колес на другой типоразмер, показатели спидометра и одометра будут отличаться от реальных скорости и пробега.
В Сети есть множество онлайн калькуляторов для вычисления таких погрешностей, но хотелось самому дойти до этого.
Все что нам надо для расчетов, это параметры старых и новых колес.
Для примера возьмем такие параметры:
Штатные диски — 14" с резиной 195/65/R14;
Новые диски — 16" с резиной 205/55/R16.
Для начала рассчитаем длину окружности колеса (L):
L = D * 3,14
Диаметр колеса (D) складывается из диаметра диска (d) и удвоенной высоты шины (H):
D = d + H*2
Переводим диаметр диска в миллиметры:
14": d = 14 * 2,54 * 10 = 355,6 мм
16": d = 16 * 2,54 * 10 = 406,4 мм
Высчитываем высоту шины (H):
14": H = 195 * 0,65 = 126,75 мм
16": H = 205 * 0,55 = 112,75 мм
Теперь можно посчитать общий диаметр колеса (D):
14": D = 355,6 + 126,75 * 2 = 609,1 мм
16": D = 406,4 + 112,75 * 2 = 631,9 мм
Тогда длина окружности колеса (L) будет равна:
14": L = 609,1 *3,14 = 1912,6 мм
16": L = 631,9 *3,14 = 1984,2 мм
Высчитаем на сколько процентов длина окружности новых колес больше старых:
(1984,2 — 1912,6) / 1912,6 *100 = 3,74%
Итак, реальная скорость и пробег будут
превышать показатели спидометра и одометра на новых колесах на 3,74%.
Например:
Скорость на спидометре 100 км/ч — Скорость реальная 103,74 км/ч
Пробег по одометру 500 км — Реальный пробег 518,72 км
И в качестве бонуса посчитаем на сколько изменилась высота машины при установке новых колес. Для этого надо узнать разницу полных радиусов:
h = (631,9 — 609,1) / 2 = 11,4 мм = 1,14 см
Обычно, когда говорят о перемещении, мы представляем себе объект, который движется по прямой. Скорость такого движения принято называть линейной, и расчёт ее средней величины выполняется просто: достаточно найти отношение пройденного расстояния к времени, за которое оно было телом преодолено. Если же объект перемещается по окружности, то в этом случае уже определяется не линейная, а угловая скорость. Что это за величина и как ее рассчитывают? Об этом как раз и пойдет разговор в данной статье.

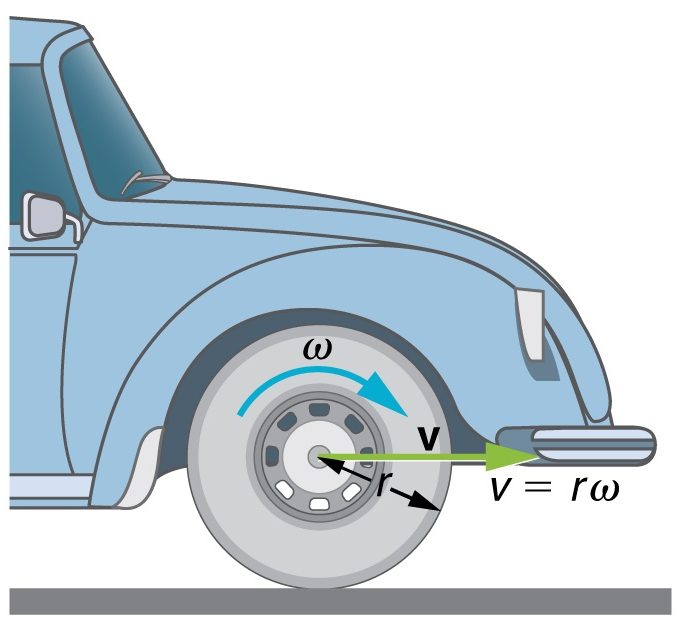
Угловая скорость: понятие и формула
Когда материальная точка движется по окружности, быстроту ее перемещения можно характеризовать величиной угла поворота радиуса, который соединяет движущийся объект с центром данной окружности. Понятно, что эта величина в зависимости от времени постоянно меняется. Быстрота, с которой этот процесс происходит, и есть не что иное, как угловая скорость. Другими словами, это отношение величины отклонения радиус-вектора объекта к промежутку времени, которое потребовалось объекту на совершение такого поворота. Формула угловой скорости (1) может быть записана в таком виде:
φ – угол поворота радиуса,
t – период времени вращения.
Единицы измерения величины
В международной системе общепринятых единиц (СИ) для характеристики поворотов принято использовать радианы. Поэтому 1 рад/с – основная единица, которая используется в расчетах угловой скорости. В то же время никто не запрещает применять градусы (напомним, что один радиан равен 180/пи, или 57˚18’). Также угловая скорость может выражаться в числе оборотов за минуту или за секунду. Если перемещение по окружности происходит равномерно, то данная величина может быть найдена по формуле (2):
где n – частота вращения.
В противном случае подобно тому, как это делают для обычной скорости, рассчитывают среднюю, или мгновенную угловую скорость. Следует отметить, что рассматриваемая величина является векторной. Для определения ее направления обычно используют правило буравчика, которое часто применяется в физике. Вектор угловой скорости направлен в ту же сторону, в которую происходит поступательное движение винта с правой резьбой. Другими словами, он устремлен вдоль оси, вокруг которой вращается тело, в ту сторону, откуда вращение видно происходящим против движения часовой стрелки.
Примеры расчета
Предположим, требуется определить, чему равна линейная и угловая скорость колеса, если известно, что его диаметр равен одному метру, а угол вращения изменяется в соответствии с законом φ=7t. Воспользуемся нашей первой формулой:
w = φ / t = 7t / t = 7 с -1 .
Это и будет искомая угловая скорость. Теперь перейдем к поиску привычной нам быстроты перемещения. Как известно, v = s / t. Учитывая, что s в нашем случае – это длина окружности колеса (l =2π*r), а 2π - один полный оборот, получается следующее:
v = 2π*r / t = w * r = 7 * 0.5 = 3.5 м/с
Вот еще одна задачка на эту тему. Известно, что радиус Земли на экваторе равен 6370 километров. Требуется определить линейную и угловую быстроту движения точек, находящихся на этой параллели, которое возникает в результате вращения нашей планеты вокруг своей оси. В данном случае нам понадобится вторая формула:
w = 2π*n = 2*3,14 *(1/(24*3600)) = 7,268 *10 -5 рад/с.
Осталось выяснить, чему равна линейная скорость: v = w*r = 7,268 *10 -5 *6370 * 1000 = 463 м/с.
Читайте также:

