Функция распределения показательного закона с параметром лямбда
Убедимся в том, что перед нами не «подделка». Поскольку и несобственный интеграл:
, то функция действительно задаёт закон распределения НСВ.
Большим достоинством показательного распределения является тот факт, что оно определяется всего лишь одним параметром. Всего лишь одним, Карл! …нет, лучше, конечно, вообще отсутствие параметров, но дальше их количество будет только возрастать =)
Как-то так получилось, что во всех примерах статьи о равномерном распределении мы начинали с функции , и поэтому для разнообразия зайдём в лес с другой стороны:
Непрерывная случайная величина задана своей функцией распределения:
1) определить коэффициент ;
2) найти плотность распределения вероятностей ;
3) схематично построить графики функций и ;
4) вычислить математическое ожидание и дисперсию ;
5) определить вероятность того, что примет значение из интервала .
Одним словом, обычная задача на НСВ бессмысленная и беспощадная.
Решаем:
1) В силу непрерывности функции распределения:
– при этом и только при этом значении предложенная функция задаёт закон распределения непрерывной случайной величины:
Пока, кстати, мы не знаем, что это за закон, ведь вверху я привёл другое определение.
2) Найдём функцию плотности распределения:
надеюсь, все в ладах с производной сложной функции: .
Ну вот, теперь избушка повернулась к нам передом, а к лесу задом. Поскольку данная функция имеет вид , то случайная величина распределена показательно. Даже образцово-показательно, т.к. значение наиболее приятно.
3) Условие допускает схематическое построение графиков, но зачем занижать планку? Даже при их ручном построении не составляет никакого труда найти пару дополнительных точек и проявить маломальскую аккуратность.
Вычислим пару значений и простенький предел . Таким образом, прямая является горизонтальной асимптотой для графика при : 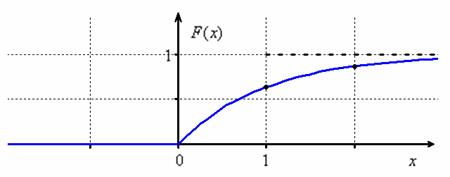
Показательное распределение нашло широкое применение в прикладных задачах, и пока чертёж «не уехал вверх» я приведу конкретный пример. Пусть переменная «икс» обозначает время и в момент времени начинает эксплуатироваться некий прибор, например, обычная лампочка. Случайная величина – время работы лампочки до перегорания. Тогда функция описывает вероятность того, что лампочка проработает МЕНЬШЕ, чем прошедшее время . И по понятным причинам при увеличении эта вероятность стремится к единице, что хорошо иллюстрирует вышеприведённый график.
Кстати, о чём идёт речь в 5-м пункте условия? В контексте рассматриваемого примера, нам нужно найти – вероятность того, что лампочка проработает более 2 тыс. часов (значения, естественно, условные). Давайте сразу и вычислим эту вероятность:
Ситуацию наглядно иллюстрирует чертёж ПЛОТНОСТИ распределения вероятностей: 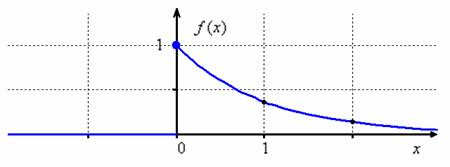
Площадь между графиком и осью абсцисс равна единице (проверено в начале статьи), и значительная часть этой площади (а именно, ) сосредоточена на промежутке от 0 до 2.
Применительно к «электрическому» примеру, определённый интеграл равен вероятности того, что лампочка проработает от 0 до тыс. часов. В частности, как раз:
.
И, наверное, все поняли, что несобственный интеграл – есть вероятность того, что лампочка проработает более тыс. часов, и Пункт 5 можно решить вторым способом:
4) Вычислим математическое ожидание и дисперсию.
Здесь есть короткий путь, и есть универсальный. Начнём с общей формулы математического ожидания, которая приводит нас к следующему несобственному интегралу:
Сначала удобно найти неопределенный интеграл:
, произвольную константу приплюсовывать не надо, т.к. она всё равно сократится:
Дробь по той причине, что знаменатель более высокого порядка роста, чем числитель.
…вот видите, как нам пригодился математический анализ, а вы всё говорили «зачем это нужно, зачем это нужно» =)
Дисперсию вычислим по формуле:
И из избушки на курьих ножках появляется следующий интеграл:
Как и в случае с матожиданием, сначала проясним первообразную:
По канонам жанра тут нужно дважды интегрировать по частям, но решение облегчается тем, что после 1-го применения формулы мы сталкиваемся с только что решённым интегралом:
Таким образом, несобственный интеграл:
Здесь по той же самой причине – порядок роста.
И, наконец, дисперсия:
«Наконец», потому что Пункт 5) уже разобран вместе с его ламповым смыслом =)
Пункты решения можно переставлять, т.к. они бывают расположены неудобно, а иногда и совершенно несуразно.
Показательное распределение нашло широкое применение в теории надёжности, и этой теме даже посвящены отдельные главы учебного пособия В.Е. Гмурмана. Помимо лампочек и более грустных примеров существуют и другие приложения. Так, например, в простейшем потоке событий, время ожидания каждого последующего события распределено по экспоненциальному закону. Проанализируйте работу диспетчера такси самостоятельно.
И для самостоятельного решения я предлагаю вам не только интересное, но ещё и крайне полезное Задание:
1) Дать определение показательного распределения вторым способом, с помощью функции распределения.
В начале статьи я привёл формулировку через плотность , и теперь ваша очередь – найдите функцию и запишите грамотный ответ на поставленный вопрос.
2) Вывести формулы математического ожидания и дисперсии.
Фактически тут нужно решить задачу в общем виде.
3) Записать закон распределения для и вычислить и .
Полученными формулами можно пользоваться и на практике, но с оглядкой. Будьте готовы к тому, что вас попросят привести подробные выкладки.
Дополнительных примеров с показательным распределением совсем немного. Впрочем, мы только что охватили все возможные случаи =) Вот она, мощь одного параметра.
Да, в сводном справочнике по теории вероятностей, конечно, приведены все частные формулы, но очень важно, чтобы вы умели получать их самостоятельно, исходя из общих определений. Это один из основополагающих принципов изучения математики, который красной нитью проходит через все её разделы.
Ну а сейчас пришло время зажечь новые огни и перейти к кульминационной статье под названием Нормальное распределение вероятностей.
1) Составим функцию :
– На интервале и .
– На промежутке , следовательно:
Показательным называют распределение, которое характеризуется функцией:
, где
2) Вычислим математическое ожидание:
Сначала найдём неопределённый интеграл:
Интегрируем по частям:
Дисперсию вычислим по формуле:
Сначала найдём неопределенный интеграл:
Интегрируем по частям:
чтобы воспользоваться уже известным интегралом, умножим и разделим на «лямбда»:
На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ - распределенных по показательному (или экспоненциальному) закону.
Плотность распределения величины $X$ с экспоненциальным законом распределения задается формулой:
Функция распределения величины $X$:
Здесь $\lambda$ - единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: $M(X)=1/\lambda$, $D(X)=1/\lambda^2$.
Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр $\lambda$ описываетс среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.
В этом разделе мы приведем разные примеры задач с полным решением, где используются показательно распределенные случайные величины.
Примеры решений
Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 часов прибор не выйдет из строя.
Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?
Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $\lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.
Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^<-2t>$ при $t\ge 0$ и $f(t)=0$ при $t\lt 0$.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Задача 5. Предполагая, что случайное время обслуживания абонента службой «09» распределено по показательному закону и средняя продолжительность обслуживания составляет 1,5 минуты, найдите вероятность того, что абонент будет обслужен более, чем за 2 минуты.
Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.
Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^<-3x>$ при $x \gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.
Задача 8. Непрерывная случайная величина $\xi$ распределена по показательному закону с параметром $\lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $\xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $\xi$ и вероятность того, что $\xi$ принимает значения, меньшие своего математического ожидания.
Задача 9. Случайная величина $\xi$ распределена по показательному закону с параметром 2. Найти $M_<\xi>$, $D_<\xi>$ вероятность попадания $\xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $\xi$.
Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(\lambda)$. Найдите вероятность события $|Х - МХ | \lt 3\sigma$ ("правило $3\sigma$" для показательного распределения).
Кривая распределения Р(Х) и график функции распределения приведены на рис. 8.13.
Для случайной величины, распределенной по показательному закону
Вероятность попадания в интервал непрерывной случайной величины Х, распределенной по показательному закону
Замечание. Показательный закон распределения вероятностей встречается во многих задачах, связанных с простейшим потоком событий. Под Потоком событий понимают последовательность событий, наступающих одно за другим в случайные моменты. Например, поток вызовов на телефонной станции, поток заявок в системе массового обслуживания и др.
Пример 8.18. Непрерывная величина Х распределена по показательному закону
Найти вероятность попадания значений величины Х в интервал .
Решение. Поскольку , то
Пример 8.19. Записать плотность распределения и функцию распределения показательного закона, если параметр . Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, распределенной по этому закону.
Решение. Так как , то плотность распределения
Функция распределения имеет вид
Поскольку для показательного закона
А по условию , то
Пример 8.20. Установлено, что время ремонта магнитофонов есть случайная величина Х, распределенная по показательному закону. Определить вероятность того, что на ремонт магнитофона потребуется не менее 15 дней, если среднее время ремонта магнитофонов составляет 12 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины Х.
Решение. По условию математическое ожидание , откуда параметр . Тогда плотность вероятности и функция распределения имеют вид: ; . Искомую вероятность можно найти, интегрируя плотность вероятности, т. е.
Но проще использовать функцию распределения
Среднее квадратическое отклонение Дней.
Пример 8.21. Найти асимметрию показательного распределения.
Решение. Так как асимметрия , а , то найдем вначале центральный момент третьего порядка
Интегрируя дважды по частям, получим
Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого определяет Вероятность отказа элемента за время длительностью T. Здесь Т — длительность времени безотказной работы элемента, — интенсивность отказов (среднее число отказов в единицу времени).
Функция надежности определяет вероятность безотказной работы элемента за время длительностью T.
Пример 8.22. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента ; для второго ; для третьего элемента Найти вероятности того, что в интервале времени часов откажут: а) только один элемент; б) только два элемента; в) все три элемента.
Непрерывная случайная величина $X$ подчиняется показательному (экспоненциальному) закону распределения вероятностей, если ее плотность распределения вероятностей $f\left(x\right)$ имеет следующий вид:
Тогда функция распределения:
Графики функций плотности $f\left(x\right)$ и распределения $F\left(x\right)$ представлены на рисунке:

Для показательного закона распределения числовые характеристики могут быть вычислены по известным формулам. Математическое ожидание и среднее квадратическое отклонение равны между собой и равны $1/\lambda $, то есть:
Параметр распределения $\lambda $ в статистическом смысле характеризует среднее число событий, наступающих в единицу времени. Так, если средняя продолжительность безотказной работы прибора равна $1/\lambda $, то параметр $\lambda $ будет характеризовать среднее число отказов в единицу времени. Примерами случайных величин, подчиненных показательному закону распределения, могут быть:
- Продолжительность телефонного разговора;
- Затраты времени на обслуживание покупателя;
- Период времени работы прибора между поломками;
- Промежутки времени между появлениями автомашин на автозаправочной станции.
Пример. Случайная величина $X$ распределена по показательному закону $f\left(x\right)=\left\<\begin
0,\ x < 0\\
5e^<-5x>,\ x\ge 0
\end
Пример. Время работы прибора — случайная величина $X$, подчиненная показательному распределению. Известно, что среднее время работы данного прибора составляет $500$ часов. Какова вероятность того, что данный прибор проработает не менее $600$ часов?
Математическое ожидание случайной величины $X$ равно $M\left(X\right)=500=1/\lambda $, отсюда параметр распределения $\lambda =1/500=0,002.$ Можем записать функцию распределения:
Тогда вероятность того, что прибор проработает менее $600$ часов, равна:
$$P\left(X\ge 600\right)=1-P\left(X < 600\right)=1-F\left(600\right)=1-\left(1-e^<-0,002\cdot 600>\right)\approx 0,301.$$
Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения, если её плотность вероятности имеет вид:

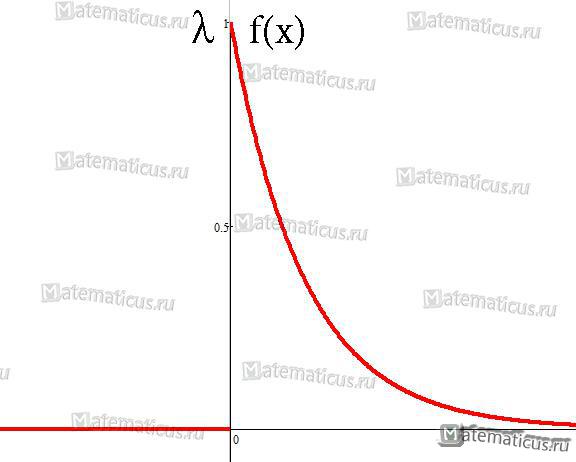
График плотности распределения случайной величины по показательному (экспоненциальному) закону
Функция распределения F(X) случайной величины X, распределенной по показательному закону, выражается формулой:
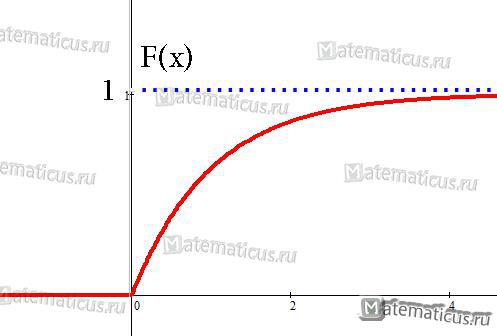
График функции распределения случайной величины по показательному (экспоненциальному) закону
Математическое ожидание равно:
Дисперсия равна:
Среднеквадратическое отклонение (СКО) равно:
Вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a, b), находится по формуле:
P(a<X<b)=e −λa −e −λb
Показательное распределение применяют в теории массового обслуживания и надёжности, для моделирования времени безотказной работы, длительности безаварийной работы приборов и машин, демографии и т. д. Пример, устройство после включения ломается через короткий промежуток времени.
Случайная величина X – время работы лампы накаливания. Случайная величина подчинена показательному распределению. Определить вероятность того, что время работы лампы накаливания будет не меньше 800 часов, если среднее время работы лампы накаливания 400 часов.
В соответствии с условием задачи, математическое ожидание M(x) случайной величины X равно 400 часам, отсюда следует, что
Читайте также:

