Что показывает коэффициент лямбда в уравнении кригинга

Обновлено: 08.01.2025

Кригинг ― это улучшенный геостатистический метод, который позволяет строить предполагаемую поверхность из набора точек с z-значениями. В отличие от других методов интерполяции в наборе инструментов Интерполяция (Interpolation), инструмент Кригинг (Kriging) предполагает интерактивное исследование пространственного поведения явления, представленного z-значениями, до выбора вами оптимального метода оценки для построения результирующей поверхности.

Что такое кригинг?

Инструменты интерполяции ОВР (IDW) (обратно взвешенных расстояний) и Сплайн (Spline) относятся к детерминированным методам интерполяции, поскольку они напрямую основаны на измеренных значениях, попадающих в окрестность интерполируемой точки, и на заданных математических формулах, которые определяют сглаженность результирующей поверхности. Вторая группа методов интерполяции состоит из геостатистических методов, таких как кригинг, которые основываются на статистических моделях, включающих анализ автокорреляции (статистических отношений между измеренными точками). В результате этого геостатистические методы не только имеют возможность создавать поверхность прогнозируемых значений, а также предоставляют некоторые измерения достоверности или точности прогнозируемых значений.

При кригинге предполагается, что расстояние или направление между опорными точками отражает пространственную корреляцию, которая может использоваться для объяснения изменения на поверхности. Инструмент Кригинг (Kriging) использует математическую функции для определенного количества точек или всех точек в пределах заданного радиуса, чтобы определить выходное значение для всех направлений. Кригинг - пошаговый процесс; он включает поисковый статистический анализ данных, моделирование вариограммы, создание поверхности и (дополнительно) изучение поверхности дисперсии. Кригинг лучше всего подходит, если вы знаете, что есть пространственно кореллированное расстояние или направленное смещение в данных. Он обычно используется в почвоведении и геологии.

Формула кригинга

Кригинг (Kriging) аналогичен ОВР (IDW) в том, что он взвешивает окружающие измеряемые значения, чтобы получить предсказание для неизмеренного местоположения. Основная формула для этих двух инструментов интерполяции формируется как взвешенная сумма данных:

Z(s_i) = измеряемое значение в местоположении i

λ_i = неизвестный вес для измеряемого значения в местоположении i

s₀ = местоположение прогноза

N = количество измеряемых значений

В ОВР вес, λ_i, зависит только от расстояния до местоположения прогноза. Однако, при использовании метода кригинга, весы основаны не только на расстоянии между измеряемыми точками и местоположениями прогнозов, но также на общем пространственном расположении измеряемых точек. Чтобы использовать пространственное расположение в весах, нужно определить количество пространственной автокорреляции. Таким образом, в обычном кригинге вес λ_i зависит от установленной модели для измеряемых точек, от расстояния до местоположения прогноза и от пространственных отношений между измеряемыми значениями вокруг местоположения прогноза. В следующих разделах обсуждается, как используется формула общего кригинга для создания карты прогнозируемой поверхности и карты точности прогнозов.

Создание карты прогнозируемой поверхности с помощью кригинга

Чтобы сделать прогноз с помощью метода интерполяции Кригинг, необходимо две задачи:

Раскрыть зависимость правил.
Сделать прогнозы.

Чтобы реализовать эти две задачи, кригинг проходит через 2-шаговый процесс:

Он создаёт вариограммы и функции ковариации для оценки значений статистической зависимости (пространственной автокорреляции), которые зависят от модели автокорреляции (соответствующей модели).
Он прогнозирует неизвестные значения (делая прогноз).

Два отдельных шага необходимы, поскольку кригинг использует данные дважды: первый раз для оценки пространственной автокорреляции данных, а второй раз ― для вычисления прогнозов.

Вариография

Установка модели, или пространственное моделирование, также известно как структурный анализ, или вариография. В пространственном моделировании структуры измеряемых точек процесс начинается с диаграммы эмпирической вариограммы, вычисленной с помощью следующего уравнения для всех пар местоположений, разделенных расстоянием h :

Формула вовлекает вычисление разницы между квадратом значений парных местоположений.

На рисунке ниже показано создание пар одной точки (красная точка) со всеми другими измеряемыми местоположениями. Этот процесс продолжается для каждой измеряемой точки.

Вычисление разницы квадратов между парами измеряемых точек

Часто каждая пара местоположений имеет уникальное расстояние, и часто существует много пар точек. Расположение всех пар быстро становится неуправляемым. Вместо размещения каждой пары, они группируются в lag bins. Например, вычислите среднюю вариограмму для всех пар точек, расположенных друг от друга дальше 40 метров, но меньше 50 метров. Эмпирическая вариограмма - это диаграмма средних значений вариограммы на оси y и расстояние (или лаг) на оси x (см. диаграмму ниже).

Пример диаграммы эмпирической вариограммы

Пространственная автокорреляция позволяет количественно оценить основной принцип географии: ближние объекты имеют большую степень сходства, чем отдаленные. Таким образом, пары близко расположенных местоположений (крайние слева на оси x облака вариограммы) должны иметь более сходные значения (внизу на оси y облака вариограммы). По мере удаления друг от друга пары местоположений (перемещение вправо по оси x облака вариограммы) они должны стать более непохожими и получить большую разницу квадратов (перемещение вверх по оси y облака вариограммы).

Установка модели на эмпирическую вариограмму

Следующим шагом является установка модели на точки, формирующие эмпирическую вариограмму. Моделирование вариограммы - это ключевой шаг между пространственным описанием и пространственным прогнозом. Основное применение кригинга - прогноз атрибутивных значений в неопорных местоположениях. Эмпирическая вариограмма предоставляет информацию о пространственной автокорреляции наборов данных. Однако она не предоставляет информацию для всех возможных направлений и расстояний. По этой причине и чтобы убедиться, что прогнозы кригинга имеют положительные дисперсии кригинга, нужно установить модель - т.е. непрерывную функцию или кривую - на эмпирическую вариограмму. Абстрактно говоря, это аналогично анализу регрессии, в котором непрерывная линия или кривая устанавливается на точечные данные.

Чтобы установить модель на эмпирическую вариограмму, выберите функцию, которая служит моделью, например, сферического типа, который увеличивает и выравнивает большие расстояния за конкретным диапазоном (см. пример сферической модели ниже). На эмпирической вариограмме есть отклонения тоек от модели; некоторые точки находятся выше кривой модели, некоторые - ниже. Однако при добавлении тех расстояний, на которых каждая точка находится выше и ниже линии, эти два значения должны быть одинаковыми. Есть большой выбор моделей вариограмм.

Модели вариограмм

Инструмент Кригинг (Kriging) предоставляет на выбор следующие функции для моделирования эмпирической вариограммы:

Круговая
Сферическая
Экспоненциальная
Гауссова
Линейная

Выбранная модель влияет на пргноз неизвестных значений, особенно если форма кривой вблизи исходных данных значительно отличается. Чем круче кривая вблизи исходных данных, тем больше влияния на прогноз будет иметь ближайшая окрестность. В результате выходная поверхность будет менее сглаженной. Каждая модель разработана для более точного соответствия разных типов явления.

На диаграммах ниже показаны две общие модели и определяется, как различаются функции:

Пример сферической модели

На этой модели показано прогрессирующее снижение пространственной автокорреляции (то же, что увеличение вариограммы) до некоторого расстояния, за которым автокорреляция равна нулю. Сферическая модель - это одна из наиболее часто используемых моделей.

Пример сферической модели

Пример экспоненциальной модели

Эта модель применяется, если пространственная автокорреляция уменьшается экспоненциально с увеличением расстояния. Здесь автокорреляция полностью исчезает только на расстоянии бесконечности. Экспоненциальная модель также часто используется. Выбор используемой модели основан на пространственной автокорреляции данных и на предварительном знании явления.

Пример экспоненциальной модели

Более подробно математические модели описаны ниже.

Понятие вариограммы - Диапазон, порог и самородок

Как обсуждалось ранее, вариограмма изображает пространственную автокорреляцию измеряемых опорных точек. Вследствие основного принципа географии (ближние объекты более похожи), измеряемые точки, находящиеся ближе друг к другу, как правило, имеют меньшую разницу квадратов, чем точки, находящиеся дальше. Когда каждая пара местоположений была размещена после binned, через них устанавливается модель. Для описания этих моделей обычно используются диапазон, порог и самородок.

Диапазон и порог

Когда вы смотрите на модель вариограммы, вы видите, что на определённом расстоянии модель выравнивается. Расстояние, где модель сначала выравнивается, называется диапазоном. Опорные местоположения, разделённые расстояниями не превышающими диапазон, пространственно автокоррелированы, в то время как местоположения, превышающие диапазон, - нет.

Иллюстрация компонентов Диапазон (Range), Порог (Sill) и Самородок (Nugget)

Значение, в котором модель вариограммы достигает диапазона (значение на оси y), называется порогом. Частичный порог - это порог минус самородок. Самородок описан в следующем разделе.

Эффект самородка

Теоретически, на расстоянии нулевого разделения (например, лаг = 0) значение вариограммы равно 0. Однако на бесконечно маленьком расстоянии разделения, вариограмма часто изображает эффект самородка, что является значением больше 0. Если модель вариограммы пересекает ось y в значении 2, самородок будет равен 2.

Эффект самородка может включать такие атрибуты, как ошибки измерения или пространственные источники изменений на расстояниях, меньших интервалу пересчёта (или оба). Ошибка измерений возникают из-за ошибки измерительного прибора. Естественное явление может изменяться пространственно в диапазоне масштабов. Изменение в микромасштабах, меньших расстояний пересчёта, появится как часть эффекта самородка. До сбора данных, важно получить понимание масштабов пространственного изменения, в котором вы заинтересованы.

Прогнозирование

После того как вы обнаружили зависимость или автокорреляцию в данных (см. раздел Вариография выше) и завершили первое использование данных ― с применением пространственной информации в данных для вычисления расстояний и моделирования пространственной автокорреляции, ― вы можете сделать прогноз, используя установленную модель. Таким образом, эмпирическая вариограмма приостанавливается.

Теперь вы можете использовать данные, чтобы сделать прогноз. Аналогично интерполяции ОВР, кригинг формирует веса из окружающих измеренных значений для прогнозирования неизмеренных местоположений. Как в случае с интерполяцией ОВР, измеренные значения, расположенные наиболее близко к неизмеренным местоположениям, имеют наибольшее влияние. Однако веса кригинга для окружающих измеренных точек более сложные, чем веса ОВР. ОВР использует простой алгоритм на основе расстояния, а веса кригинга происходят из вариограммы, которая была разработана, глядя на пространственной характер данных. Чтобы создать непрерывную поверхность явления, для каждого местоположения, или центров ячеек, делаются прогнозы в исследуемой области на основе вариограммы и пространственной организации измеряемых значений, расположенных рядом.

Методы кригинга

Доступны два метода кригинга: ординарный и универсальный.

Ординарный кригинг - наиболее общий и широко используемый из методов кригинга, он используется по умолчанию. Предполагается, что среднее значение константы не известно. Это предположение имеет смысл, пока нет научного основания отклонить его.

При универсальном кригинге предполагается, что есть доминирующий тренд в данных - например, преобладающий ветер - и его можно моделировать детерминистской функцией, полиномом. Этот полином извлекается из исходных измеренных точек, и автокорреляция моделируется из произвольных ошибок. После установки модели на произвольные ошибки и до прогнозирования, полином добавляется обратно к прогнозам, чтобы дать значимые результаты. Универсальный кригинг следует использовать, только если вы знаете, что в данных есть тренд, и можете дать научное обоснование для его описания.

Диаграммы полувариограмм

Кригинг - это комплексная методика, которая требует более обширных знаний о пространственной статистике, чем можно рассмотреть в этом разделе. Перед тем, как воспользоваться методами кригинга, вы должны получить исчерпывающее представление об основах кригинга и оценить пригодность ваших данных для моделирования с использованием этой методики. Если вы не обладаете достаточным пониманием процедуры кригинга, настоятельно рекомендуется изучить некоторые из работ, ссылки на которые помещены в конце этой статьи.

Кригинг основывается на теории региональной переменной, которая предполагает, что пространственная вариация явления, представленного z-значениями, статистически однородна по всей поверхности (то есть, вариация примерно одинакова во всех точках поверхности). Такая гипотеза о пространственной однородности является основой теории региональной переменной.

Математические модели

Ниже приведены общие формы и уравнения математических моделей, используемых для описания (полу)дисперсии.

Иллюстрация модели сферической вариограммы Иллюстрация модели круговой вариограммы Иллюстрация модели экспоненциальной вариограммы Иллюстрация модели Гауссовой вариограммы Иллюстрация модели линейной вариограммы

Ссылки

Burrough, P. A. Principles of Geographical Information Systems for Land Resources Assessment . New York: Oxford University Press. 1986.

Heine, G. W. "A Controlled Study of Some Two-Dimensional Interpolation Methods." COGS Computer Contributions 3 (no. 2): 60–72. 1986.

McBratney, A. B., and R. Webster. "Choosing Functions for Semi-variograms of Soil Properties and Fitting Them to Sampling Estimates." Journal of Soil Science 37: 617–639. 1986.

Oliver, M. A. "Kriging: A Method of Interpolation for Geographical Information Systems." International Journal of Geographic Information Systems 4: 313–332. 1990.

Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. Numerical Recipes in C: The Art of Scientific Computing . New York: Cambridge University Press. 1988.

Royle, A. G., F. L. Clausen, and P. Frederiksen. "Practical Universal Kriging and Automatic Contouring." Geoprocessing 1: 377–394. 1981.

Задача состоит в следующем: мы имеем N значений данных z(x₁), …, z(x_N) в нашем районе, и мы хотим оценить линейную функцию переменной Z(x). Например, мы можем захотеть оценить ее значение в конкретной точке Z(x₀), или ее среднее по определенному региону. (Некоторые другие линейные функционалы, такие как градиент, также могут быть оценены с помощью кригинга.) Чтобы избежать необходимости описания всех случаев раздельно, мы обозначим оцениваемое множество через:

[7.1]

Объем V может быть всем месторождением, или добываемым блоком, или он может быть таким маленьким, как одна точка, в случае точечной оценки. Он может быть даже неправильной формы. Для большей информации по кригингу объемов неправильной формы смотрите Рамку 5. Чтобы оценить Z(V), мы запишем взвешенное среднее данных:

[7.2]

где l_i – факторы взвешивания. По договоренности звездочка будет использоваться для обозначения оценки значения, как противопоставление действительному, но неизвестному значению. Проблема заключается в определении лучшего способа выбора факторов взвешивания. Т.е. найти область, где мы можем использовать геостатистическую модель. Мы предполагаем пространственную переменную:

[7.3]

Веса выбираются такие, чтобы оценка была:

несмещенной:

с минимальной дисперсией: - минимально.

Эту дисперсию мы будем называть дисперсией кригинга.

Различные кригинговые оценщики

На первом этапе мы предполагаем, что пространственная переменная Z(x) стационарна и, что ее среднее m неизвестно. Кригинг с неизвестным средним называется обычным кригингом (OK). Сначала мы определим систему уравнений для обычного кригинга (для стационарного случая) в терминах вариограммы, а затем ковариацию, после чего покажем, как обобщить эти результаты на случай внутренних переменных.

Рамка № 5: Могут ли неправильной формы блоки быть оценены кригингом?

Некоторые люди думают, что только регулярные блоки могут быть оценены кригингом. Но это не верно. Уравнения кригинга имеют довольно общий характер. Целевой объем "V" может быть малым, как точка, или большим, как все месторождение. Чаще это блоки регулярной формы, но они могут иметь и неправильную форму, такую как блок, намеченный для взрыва.

Проблемы возникают только, когда надлежащим образом дискретизируется V для вычисления и . Для правильной формы блока легче выбрать размер сетки, который гарантирует достаточное количество точек дискритизации внутри зоны оценивания. Как можно увидеть из двух рисунков ниже, небольшое изменение интервалов сетки приводит к существенному уменьшению количества узлов сети внутри зоны.

Следующий этап заключается в том, чтобы понять, как оценивать неизвестное среднее m. После этого мы увидим, что происходит с кригинговой оценкой, если среднее m известно. Этот метод называется простым кригингом и обозначается SK. Во всех этих случаях линейные уравнения, называемые системой кригинга, должны решаться для вычисления весов кригинга и дисперсии кригинга.

Обычный кригинг

Несмещенность. Переменная Z(x) полагается стационарной со средним m. Ее среднее каждой точки равно m и, поэтому является средним любого блока. Это значит

[7.4]

Большинство оценок являются взвешенным движущимся средним величин пространственных данных, что означает, что они - линейные комбинации этих данных:

[7.5]

Среднее ошибки оценивания – это:

[7.6]

Чтобы быть несмещенной, математическое ожидание ошибки должна быть равно нулю, поэтому либо m=0, либо сумма весов кригинга равна 1. В первом случае среднее известно (Это приводит к простому кригингу). Если m неизвестно, то сумма весов должна равняться 1.[2]

Минимальная дисперсия. Дисперсию ошибки можно выразить в терминах либо ковариации, либо вариограммы:

[7.7]

где - среднее вариограммы между x_i и объемом V, т.е.

Как показано в Главе 6, является средним вариограммы между любыми двумя точками x и x', независимо распределенных по всему объему V.

Аналогично и являются средними для ковариаций. Чтобы минимизировать дисперсию оценивания при условии, что сумма весов кригинга равна 1, мы вводим коэффициент Лагранжа m в выражение для минимизации. Поскольку сумма весов должна быть равна 1.0, то добавление слагаемого m не изменит значения выражения.

[7.8]

Частная производная затем приравнивается нулю. Это приводит к системе с N+1 линейными уравнениями, называемой системой кригинга. В Рамке 6 показан вывод этой системы. Система кригинга в терминах вариограммной модели имеет вид:

[7.9]

Минимум дисперсси, называемый дисперсией кригинга вычисляется:

[7.10]

Понятно, что уравнения можно решать и в терминах ковариации, используя минимизацию первой формы [7.7]. Вид системы кригинга в этом случае:

[7.11]

Рамка № 6: Вывод уравнений обычного кригинга

Важным шагом в выводе уравнений кригинга является минимизация выражения для дисперсии оценивания:

Эта формула получена дифференцированием в отношении каждого неизвестного и присваиванием частной производной нуля. Здесь мы видим это в деталях для случая, когда имеется три пробы. Процедура такая же, как и в общем случае для N проб. Если мы установим и , тогда

Дифференцируем по l₁ и получаем

Аналогично дифференцируем по l₂ и l₃ и получаем

Последнее дифференцирование по m дает

В результате - система кригинга имеет вид:

В общем случае она должна дифференцироваться по каждому из N неизвестных весов, сумма их в системе кригинга должна быть от 1 до N, а не от 1 до 3. В противном случае принципы остаются теми же.

Два коэффициента Лагранжа связаны между собой равенством m’=-m. Получаем соответствующую дисперсию кригинга:

[7.12]

Чтобы решить систему, запишем ее в матричном виде: AX=B.

[7.13]

Если g - допустимая модель, и если нет повторяющихся точек, то матрица A в любом случае - не вырожденная. Существует ее обратная матрица A -1 . Поэтому решение существует, и можно доказать, что оно единственно. Единственность важна, потому что она используется для связи различных типов кригинга. Дисперсию кригинга можно записать:

Кригинг обрабатывает эти поверхности так, считая их образованными из трех независимых величин. Первая, называемая дрейфом или структурой ( drift or structure) поверхности, представляет поверхность как общий тренд в определенном направлении. Наконец, мы имеем случайный шум ( random noise), который не связан с общей тенденцией и не имеет пространственной автокорреляции. Кларк [ Clarke, 1990 ] удачно иллюстрирует этот набор значений посредством аналогии: когда мы идем вверх по горе, рельеф местности изменяется в восходящем направлении между отправной точкой и вершиной; это - дрейф. По пути мы встречаем локальные снижения и повышения, сопровождаемые случайными, но коррелированными высотами. [1]

Кригинг существует в двух основных формах. [2]

Кригинг часто дает довольно точные оценки пропущенных значений, но эта точность обходится ценой времени и вычислительных ресурсов. Но даже при этом кригинг имеет еще одно преимущество перед другими методами интерполяции, - он не только дает интерполированные значения, но также и оценку возможной ошибки этих значений. Это может навести на мысль, что данный метод следует применять повсеместно, но увы. Когда мы имеем дело с большим уровнем локального шума из-за ошибок измерений или большие вариации высоты между отсчетами, в данном методе становится трудным построение кривой полудисперсии. А в таких условиях результаты кригинга будут не лучше, чем полученные другими методами. [3]

Кригинг в принципе понижает оценки для блоков ( зон влияния), характеризуемых высокими значениями параметра, и повышает их для блоков с низкими значениями, но делает это с учетом взаимного расположения таких блоков и особенностей пространственной изменчивости признака. [4]

Кригинг существует в двух основных формах. [5]

Кригинг ( kriging) - методика оценки по средневзвешенным значениям и скользящей средней, по геостатистическим данным, которая использует пространственную корреляцию точечных измерений для оценки значений в прилегающих, не замеряемых точках. [6]

Наиболее эффективен кригинг при обработке результатов эксплуатационного опробования и организации управления качеством добываемого сырья. [9]

В основе кригинга лежит представление о пространственных переменных, среднее значение которых для некоторой области может быть вычислено через точечные оценки внутри и вне этой области с учетом пространственной взаимокорреляции значений переменной от расстояния между точечными наблюдениями. [10]

В случаях, когда такой взаимозависимости не наблюдается, классический кригинг не применим, но могут быть использованы некоторые эмпирические приемы корректировки результатов подсчетов. [11]

Для интерполяции данных, получаемых в точках опробования пород, методом кригинга были использованы эмпирические полуварио-граммы, аппроксимированные аналитической зависимостью (4.31); коэффициенты этого уравнения, в том числе параметр, характеризующий эффект самородков, приведены в легендах на рис. 4.17. Интерполяционная сетка для двухмерного моделирования включала 101x121 равносторонних ( Ах Лу 0 25 м) блоков. [12]

Здесь мы рассмотрим три метода интерполяции: метод обратных взвешенных расстояний ( ОВР), метод поверхности тренда и кригинг . Есть книги, детально рассматривающие и многие другие методы [ Burrough, 1983; Davis, 1986 ], здесь мы ограничимся только самыми известными. [14]

Для интерполяции пространственных данных используются различные комплексы программ для ЭВМ: метод сглаживания, метод аппроксимации, метод линейной интерполяции, метод точечного кригинга и др. Компьютерные программы позволяют непредвзято и более точно, чем указанные выше методы, провести на карте границы зон загрязнения. Наилучший метод интерполяции выбирается для каждого конкретного обследования, исходя из имеющейся информации. Особенности выполнения интерполяционных расчетов описаны в специальной литературе. Для исполнителей можно рекомендовать комплекс программ SURFER или аналогичные для персональной ЭВМ, позволяющий по опытным точкам рассчитывать концентрации в узлах регулярной сетки желаемой густоты и строить изолинии с заданным шагом. [15]

Крамера и коэффициентом "лямбда". [c.552]

Мы рассмотрим статистики, обычно используемые для оценки статистической значимости и тесноты связи переменных, в таблице сопряженности. Статистическая значимость наблюдаемой связи обычно измеряется критерием Теснота связи важна с практической точки зрения. Обычно она имеет значение, если связь статистически значимая. Тесноту связи можно измерить коэффициентом корреляции фи, коэффициентом сопряженности Крамера и коэффициентом "лямбда". Эти статистики ниже описаны детальнее. [c.575]

Таким образом, связь не очень сильна. В этом случае V = о Так всегда происходит для таблицы Другой обычно рассчитываемой статистикой является коэффициент "лямбда". [c.578]

Мера в процентах улучшения прогнозирования значения зависимой переменной при данном значении независимой переменной. Значения коэффициента "лямбда" лежат в пределах от 0 до [c.578]

Значения коэффициента "лямбда" лежат в пределах от 0 до 1. Значение "лямбда", равное О, означает, что никакого улучшения в прогнозировании не наблюдается. Значение 1 указывает на то, что прогноз может быть сделан без ошибки. Это происходит тогда, когда каждая категория независимой переменной связана с одной категорией зависимой [c.579]

Симметричный коэффициент "лямбда" не дает предположения о какая из переменных зависимая. Он измеряет общее улучшение прогнозирования, когда прогноз уже сделан в обоих направлениях. [c.579]

Если нулевая гипотеза отклонена, то определите тесноту связи, используя статистики коэффициент сопряженности, Крамера, коэффициент "лямбда" или другие статистики). [c.580]

Л (лямбда) - коэффициент Оукена [c.830]

Коэффициент "лямбда" используется в том случае, когда переменные измерены с помощью номинальной шкалы, коэффициент (asymmetri lambda) показывает выраженное в процентах улучшение при прогнозировании значения зависимой переменной при данном значении независимой переменной, [c.578]

Асимметрический коэффициент "лямбда" подсчитывают для каждой из зависимых переменных. Также рассчитывают симметричный коэффициент (symmetri lambda) — средним значением двух асимметричных значений. [c.579]

Симметричный коэффициент "лямбда" не делает предположения о том, какая из переменных зависимая. Он измеряет прогнозирования, когда прогноз уже выполнен в обоих направлениях [14]. Значение асимметричного коэффициента "лямбда" в табл. 15.3, если в качестве переменной взять Internet, равно 0,333. Это указывает на то, что знание пола нашу возможность прогнозирования на 0,333, т.е. имеет место улучшение прогнозирования на 0,33%. Симметричный коэффициент "лямбда" также равен 0,33%. [c.579]

Часто, чтобы лучше уяснить суть связи переменных, вводят третью переменную. Статистика позволяет проверить статистическую значимость наблюдаемой в таблице, s o-i-i пряженности. С помощьюкоэффициента сопряженности, V -коэффициент Крамера и коэффициента "лямбда" определяют силу связи между переменными. [c.598]

Бессмысленно интерпретировать результаты анализа, если определенные дискрими-не являются статистически значимыми. Поэтому выполнить статистическую проверку нулевой гипотезы о равенстве средних всех функций во всех группах генеральной совокупности. В программе SPSS эта проверка базируется на коэффициенте лямбда (X) Уилкса. Если одновременно проверяют несколько [c.695]

Измерители линейной чувствительности к движению финансовых переменных используются под различными обозначениями. На рынке инструментов с фиксированным доходом чувствительность к движению процентных ставок измеряется дюрацией. На рынке акций чувствительность к фактору рынка в цепом (например, фондовому индексу) называется систематическим риском или коэффициентом бета. На рынке производных инструментов чувствительность

Одним из основных геостатистических методов исследования окружающей среды является метод кригинга, согласно которому оцениваемое значение регионализованной переменной величины ψ_р в точке p определяется как взвешенное среднее известных наблюдений в соседних точках по формуле:

где W_i — вес i-го значения регионализованной переменной величины ψ_i по отношению к оцениваемой точке p из k соседних точек.

Метод кригинга предусматривает решение системы уравнений [1]:

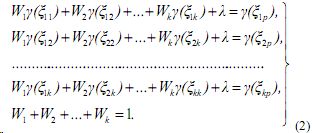
где γ(ξ_ij) — значение полувариограммы для расстояния ξ_ij между точками i и j; γ(ξ_ip) — значение полувариограммы для расстояния ξ_ip между известной точкой i и оцениваемой точкой p, λ— множитель Лагранжа.

Однако применение системы уравнений (2) нередко приводит к тому, что некоторые веса W_i оказываются либо меньше нуля, либо больше 1. В частности, такие результаты приведены Дэвисом [1]. Очевидно, это существенно искажает физический и математический смысл весов W_i и приводит к неправильной оценке величины ψ_p.

Подобные результаты могут быть вызваны либо неточным подбором модели полувариограммы, либо наличием среди точек наблюдений величины ψ_i точек, не оказывающих практического влияния на оцениваемое значение ψ_р. Такие точки должны иметь веса, равные нулю.

Дисперсия оценки методом кригинга может быть выражена формулой Матерона [2]:

где - дисперсия ПЭС относительно ее среднего значения; - ковариация среднего значения и значения ; - ковариация значений и .

Система уравнений (2) выводится из условия минимума дисперсии в формуле (3), условия для весов W_i :

а также заменой ковариаций и соответственно на разности и .

Однако, если подставить в формулы (3) и (4) вместо W_i () и выводить систему уравнений кригинга относительно , а затем сделать обратную подстановку (W_i вместо ), то получается система уравнений кригинга

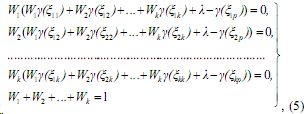
позволяющая учесть ограничения.

Так как решение системы уравнений (5) может быть затруднено из-за ее нелинейности, то для ее компьютерного решения предлагается следующий алгоритм:

Решить систему линейных уравнений (2).

Если полученное решение не отвечает ограничениям , то исключить из рассмотрения точку наблюдения с наименьшим отрицательным весом (или присвоить ему значение ноль), иначе - закончить вычисления.

Перейти после указанных изменений к пункту 1.

Полученное при реализации данного алгоритма (или использования формулы (5)) решение позволяет учесть ограничения и точнее оценить значение регионализованной переменной величины ψ_р.

Читайте также: