В вертикально расположенном цилиндре под невесомым поршнем находится газ расстояние от поршня до дна
32. Работа газа. Первое начало термодинамики: задачи с ответами без решений
(Все задачи по молекулярно-кинетической теории и ответы к ним находятся в zip-архиве (290 кб), который можно скачать и открыть на своем компьютере. Попробуйте решить задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)
32.1. Какова внутренняя энергия одноатомного газа, занимающего при температуре T объем V, если концентрация молекул n? [ U = (3/2)nkTV ]
32.2. В цилиндре с площадью основания S = 100 см 2 находится газ при температуре t = 27 °С. На высоте h = 30 см от дна цилиндра расположен поршень массой m = 60 кг. Какую работу совершит газ, если его температуру медленно повысить на Δt = 50 °С? Атмосферное давление po = 10 5 Па. [ A ≅ 79.4 Дж ]
32.3. Газообразный водород массой m = 0,1 кг совершает круговой процесс 1 – 2 – 3 – 1 (рис.). Найдите работу газа на участке 1 – 2, если Т1 = 300 K, a V2 = 3V1. [ A = 2.5×10 5 Дж ]
32.4. Идеальный газ массой m = 20 г и молярной массой M = 28 г/моль совершает замкнутый процесс (рис.). Температура в точках 1 и 2 равна: T1 = 300 К; Т2 = 496 К. Найти работу газа за цикл. [ A = 1162 Дж ]
32.5. Давление ν молей идеального газа связано с температурой по закону: Т = αp 2 (α = const). Найти работу газа при увеличении объема от значения V1 до значения V2. Выделяется или поглощается при этом тепло? [смотрите ответ в общем файле темы]
32.6. В цилиндре под невесомым поршнем находится газ. Поршень связан с дном цилиндра пружиной. Газ расширяется из состояния с параметрами p1, V1 в состояние p2, V2. Определить работу газа. [смотрите ответ в общем файле темы]
32.7. ν молей идеального газа помещены в герметическую упругую оболочку. Упругость оболочки такова, что квадрат объема пропорционален температуре. На сколько изменится энергия оболочки, если газ нагреть от температуры T1 до температуры T2? Какова теплоемкость системы? Теплоемкостью оболочки и внешним давлением пренебречь. [смотрите ответ в общем файле темы]
32.8. При изотермическом процессе газ совершил работу 1000 Дж. На сколько увеличится внутренняя энергия этого газа, если ему сообщить количество теплоты вдвое больше, чем в первом случае, а процесс проводить изохорически? [2000 Дж]
32.9. Найти количество теплоты, сообщенное газу в процессе 1 – 2 (рис.). [ Q = 3pV/4 ]
32.10. Один моль идеального газа совершает процесс 1 – 2 – 3 (рис.). Известны: давление p1, p2 и объем V1, V2. Найти поглощенное газом в этом процессе количество теплоты. [смотрите ответ в общем файле темы]
32.11. Один моль идеального газа нагревают сначала изотермически. При этом он совершает работу 10 Дж. Затем его нагревают изобарически, сообщая ему то же количество теплоты. Какую работу совершает газ во втором случае? [4 Дж]
32.12. Водород массой m = 1 кг при начальной температуре T1 = 300 K охлаждают изохорически так, что его давление падает в η = 3 раза. Затем газ расширяют при постоянном давлении до начальной температуры. Найти произведенную газом работу. [ A = 8.3×10 5 Дж ]
32.13. Один моль идеального газа переводят из начального состояния 1 в конечное 4 в процессе, представленном на рис. Какое количество теплоты подвели к газу, если ΔT = Т4 − T1 = 100 K? [ Q = 415 Дж ]
32.14. В вертикальном цилиндре под тяжелым поршнем находится газ при температуре T. Масса поршня m, его площадь S, объем газа V. Для повышения температуры газа на ΔT ему сообщили количество теплоты Q. Найдите изменение внутренней энергии газа. Атмосферное давление po, трения нет. [смотрите ответ в общем файле темы]
32.15. Для нагревания некоторого количества газа с молярной массой M = 28 г/моль на ΔT = 14 K при p = const требуется количество теплоты Q = 10 Дж. Чтобы охладить его на ту же ΔT при V = const требуется отнять Q = 8 Дж. Определить массу газа. [ m ≅ 0.48 г ]
32.16. В вертикальном цилиндре на высоте h от дна находится поршень. Под поршнем — идеальный газ. На поршень положили гирю массой m. После установления теплового равновесия с окружающей средой цилиндр теплоизолировали и газ начали нагревать. Какое количество теплоты следует подвести к газу, чтобы поршень вернулся в исходное положение. Трения нет. [ Q = 5mgh/2 ]
32.17. В вертикальном цилиндре под невесомым поршнем находится гелий. Объем гелия Vo, а давление 3po (po – атмосферное давление). Поршень удерживается сверху упорами (рис.). Какое количество теплоты необходимо отнять у гелия чтобы его объем стал Vo/2. Трения нет. [ Q = 17poVo/4 ]
32.19. Теплоизолированный сосуд объемом V = 22,4 л разделен пополам теплопроводящей перегородкой. В первую половину сосуда вводят m1 = 11,2 г азота при температуре t1 = 20 °С, а во вторую – m2 = 16,8 г азота при t2 = 15 °С. Какое давление установится в первой половине после выравнивания температур? Система теплоизолирована. [ p ≅ 86 кПа ]
32.20. Баллон емкостью V1 содержащий ν1 молей газа при температуре T1, соединяют с баллоном емкостью V2, содержащим ν2 молей того же газа при температуре T2. Какие установятся давление и температура. Система теплоизолирована. [смотрите ответ в общем файле темы]
32.21. Над одним молем идеального газа совершается процесс из двух изохор и двух изобар (рис.). Температуры в точках 1 и 3 равны T1 и T3. Определить работу газа за цикл, если точки 2 и 4 лежат на одной изотерме. [смотрите ответ в общем файле темы]
32.22. Моль идеального газа совершает цикл из двух изохор и двух изобар (рис.). Работа газа за цикл A = 200 Дж. Максимальная и минимальная температуры в цикле отличаются на ΔT = 60 К. Отношение давлений на изобарах равно 2. Найти отношение объемов на изохорах. [ ≅ 3 ]
32.23. Внутри цилиндрического сосуда под поршнем массы m находится идеальный газ под давлением p. Площадь поршня S, внешнего давления нет. Вначале поршень удерживается на расстоянии h1 от дна сосуда (рис.). Поршень отпустили. После прекращения колебаний поршень остановился. На каком расстоянии от дна он остановился? Трения нет. Тепловыми потерями и теплоемкостью поршня и цилиндра пренебречь. [смотрите ответ в общем файле темы]
32.24. В гладкой трубке между двумя поршнями массой m находится один моль идеального газа. В начальный момент скорости поршней направлены в одну сторону и равны v и 3v (рис.), а температура газа To. Найти максимальную температуру газа. Внешнего давления и трения нет. [смотрите ответ в общем файле темы]
32.25. В горизонтальном неподвижном цилиндре, закрытом поршнем массы m, находится один моль идеального газа. Газ нагревают. При этом поршень, двигаясь равномерно, приобретает скорость v. Найдите количество теплоты, сообщенное газу. Теплоемкостью сосуда и поршня, а также внешним давлением пренебречь. [ Q = 5mv 2 /4 ]
32.26. Сосуд, содержащий некоторое количество азота, движется со скоростью v = 100 м/с. На сколько изменится температура азота, если сосуд внезапно остановить? [ ΔT = Mv 2 /(5R) ]
32.27. В гладкой горизонтальной трубе находятся два поршня массами m и 3m. Между поршнями идеальный газ при давлении po. Объем между поршнями Vo (рис.). Первоначально поршни неподвижны, затем их отпускают. Найти максимальные скорости поршней. Труба длинная, внешнего давления нет. [смотрите ответ в общем файле темы]
32.28. Один моль идеального газа изобарически нагрели на ΔT = 72 K, сообщив ему количество теплоты Q = 1,6 кДж. Найти величину γ = cp/cV. [ γ = 1.6 ]
32.29. Вычислить γ = cp/cV для газовой смеси, состоящей из ν1 = 2 молей кислорода и ν2 = 3 молей углекислого газа. [ γ ≅ 1,6]
32.30. Теплоизолированный небольшой сосуд откачан до глубокого вакуума. Окружающая сосуд атмосфера состоит из идеального одноатомного газа при температуре 300 К. В сосуде открывается небольшое отверстие и он заполняется газом. Какую температуру будет иметь газ в сосуде сразу после заполнения? [500 K]
32.31. Определить скорость истечения гелия из теплоизолированного сосуда в вакуум через малое отверстие. Температура газа в сосуде T = 1000 K, скоростью газа в сосуде пренебречь. [ v ≅ 3.3×10 3 м/с]
32.32. Горизонтальный цилиндрический сосуд разделен подвижным поршнем. Справа от поршня одноатомный идеальный газ с параметрами: po; Vo; To, слева – вакуум (рис.). Поршень соединен с левым торцом цилиндра пружиной, собственная длина которой равна длине сосуда. Определить теплоемкость системы в этом состоянии. Теплоемкостью поршня и цилиндра пренебречь. Трения нет. [ C = 2poVo/To ]
32.33. Над идеальным двухатомным газом совершают процесс p = αV (α = const). Какова молярная теплоемкость газа в этом процессе? [c = 3R]
32.34. С одним молем идеального одноатомного газа проводят процесс: p = po — αV, где α – известная константа. Определить, при каких значениях объема газ получает тепло, а при каких отдает. Объем в процессе возрастает.
32.35. В процессе расширения азота его объем увеличился на 2 %, а давление уменьшилось на 1 %. Какая часть теплоты, полученной азотом, была превращена в работу? Удельная теплоемкость азота при постоянном объеме cV = 745 Дж/(кг • К). [ ≅ 0.44 ]
32.36. В цилиндрическом горизонтальном сосуде находится гладкий подвижный поршень. Слева и справа от поршня находится по одному молю идеального одноатомного газа. Температура газа в левой части поддерживается постоянной, а газ в правой части нагревается. Найдите теплоемкость газа в правой части в момент, когда поршень делит сосуд пополам. [C = 2R]
32.37. В вертикальном цилиндре под поршнем площадью S и массой m находится 1 моль идеального одноатомного газа. Под поршнем включается нагреватель, мощность которого N. Определите установившуюся скорость движения поршня. Атмосферное давление po, газ теплоизолирован, трения нет. [смотрите ответ в общем файле темы]
32.38. Мыльный пузырь содержит ν молей идеального одноатомного газа. Определить теплоемкость этой системы. Атмосферное давление не учитывать. [ C = 3νR ]
32.39. По трубе, в которой работает электрический нагреватель, пропускают газ (рис.). Определить мощность нагревателя, если разность температур газа на выходе и на входе равна ΔТ = 5 К, а массовый расход газа μ = 720 кг/ч. Молярная теплоемкость газа при постоянном давлении cp = 29,3 Дж/(моль • К), его молярная масса M = 29 г/моль. [ N ≅ 1.01 кВт ]
32.40. Из небольшого отверстия в баллоне с сжатым гелием вытекает струя гелия со скоростью v. Найдите разность температур гелия в баллоне и в струе. Давление в струе считать равным внешнему давлению, скоростью газа в баллоне пренебречь. [ ΔT = Mv 2 /(5R) ]
32.41. Одинаковые сообщающиеся сосуды закрыты поршнями массой m = 5 кг и M = 10 кг и соединены тонкой трубкой с краном (рис.). Под поршнями идеальный одноатомный одинаковый газ. Сначала кран закрыт, поршень M находится на высоте H = 10 см от дна, а температура одинакова. На какую высоту передвинется поршень m после открытия крана? Система теплоизолирована, атмосферного давления нет. [ 20 см ]
32.42. В горизонтальной открытой трубе сечением S без трения могут двигаться два поршня массами m и M. Начальное расстояние между поршнями l, атмосферное давление po. При закрепленных поршнях воздух между ними откачали, затем поршни отпустили. Какое количество теплоты выделится в результате их абсолютно неупругого столкновения? [ Q = poSl ]
32.43. Один моль идеального газа совершает цикл 1 – 2 – 3 – 1, состоящий из изохоры 1 – 2 и двух процессов, представляемых отрезками прямых в координатах p – V (рис.). Определить работу газа за цикл, если известны: температура T1, Т2 = 4Т1, а также Т2 = Т3. Линия 3 – 1 проходит через начало координат. [ A = 3RT1/2 ]
В вертикально расположенном цилиндре под невесомым поршнем находится газ расстояние от поршня до дна
Варианты задач ЕГЭ
разных лет
(с решениями).
1. Воздушный шар объемом 2500 м 3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Температура окружающего воздуха 7°С, его плотность 1,2 кг/м 3 . Оболочку шара считать нерастяжимой. (Решение)
2. Воздушный шар объемом 2500 м 3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Рассчитайте максимальную массу груза, который может поднять шар, если воздух в нем нагреть до температуры 77°С. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м 3 . Оболочку шара считать нерастяжимой. (Решение)
3. Воздушный шар объемом 2500 м 3 имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Если температура окружающего воздуха 7°С, а его плотность 1,2 кг/м 3 , то при нагревании воздуха в шаре до температуры 77°С шар поднимает груз с максимальной массой 200 кг. Какова масса оболочки шара? Оболочку шара считать нерастяжимой. (Решение)
4. Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 10 5 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
5. Воздушный шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием. Он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 10 5 Па, груз массой 225 кг. Какова масса гелия в оболочке шара? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)

6. При исследовании уравнения состояния газа ученик соединил сосуд (1) объемом 150 мл с манометром (2) тонкой трубкой и опустил сосуд в горячую воду (см. рисунок). Чему равна плотность воздуха в сосуде? Начальные показания манометра равны 0 мм рт. ст. Шкала манометра и нижняя шкала барометра (3) проградуированы в мм рт. ст. Верхняя шкала барометра проградуирована в кПа. Объем измерительного механизма манометра и соединительной трубки значительно меньше 150 мл. (Решение)
7. Теплоизолированный сосуд объемом V = 2 м 3 разделен пористой неподвижной перегородкой на две равные части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона — нет. В начальный момент в одной части сосуда находится νHe = 2 моль гелия, а в другой — νAr = 1 моль аргона. Температура гелия TНe = 300 К, а температура аргона ТAr = 600 К. Определите температуру гелия после установления равновесия в системе. (Решение)
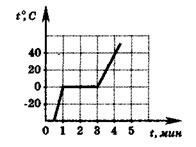
8. На рисунке представлен график изменения температуры вещества в калориметре с течением времени. Теплоемкостью калориметра и тепловыми потерями можно пренебречь и считать, что подводимая к сосуду мощность постоянна. Рассчитайте удельную теплоемкость вещества в жидком состоянии. Удельная теплота плавления вещества равна 100 кДж/кг. В начальный момент времени вещество находилось в твердом состоянии. (Решение)
9. В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают вдвигать в сосуд. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса пара в сосуде? Ответ поясните. (Решение)
10. В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают вдвигать в сосуд. При этом температура воды и пара остается неизменной. Как будет меняться при этом отношение массы пара к массе жидкости в сосуде? Ответ поясните. (Решение)
11. В цилиндр объемом 0,5 м 3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10 -4 м 2 , расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину стержня, если его можно считать невесомым. (Решение)
12. В цилиндр объемом 0,5 м 3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок к зад. 11). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10 -4 м 2 , расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину AB. (Решение)
13. Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 10 5 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
14. Воздушный шар, оболочка которого имеет массу М = 145 кг и объем V = 230 м 3 , наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t0 = 0°C. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие. (Решение)
15. В высоком вертикальном цилиндрическом сосуде под тяжелым поршнем, способным перемещаться вдоль стенок сосуда практически без трения, находится некоторое количество воздуха под давлением p = 1,5 атм. Поршень находится в равновесии на высоте H1 = 20 см над дном сосуда. Определите, на какое расстояние ΔH сместится поршень, если сосуд перевернуть открытым концом вниз и дождаться установления равновесия. Считать температуру воздуха и атмосферное давление p0 = 1 атм постоянными. Массой воздуха в сосуде по сравнению с массой поршня можно пренебречь. (Решение)
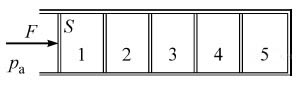
16. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 100 см 2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 10 5 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 2 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Какого значения достигнет F, когда объём газа в самом правом, 5-м отсеке цилиндра уменьшится в n = 2 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими. (Решение)
17. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 50 см 2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 10 5 Па окружающей цилиндр атмосферы (см. рисунок к зад 16). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 4 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Когда давление газа в самом правом, пятом отсеке цилиндра, увеличится в n = 3 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими. (Решение)
18. Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно p. Определить давление p1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной. (Решение)
19. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при атмосферном давлении 10 5 Па. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружающего воздуха одинакова и равна 0°С. (Площадь сферы S= 4πr 2 , объем шара V = 4/3πr 3 .) (Решение)
20. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см 2 . Давление окружающего воздуха p = 10 5 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. Какое количество теплоты нужно отвести от газа при его медленном охлаждении, чтобы поршень передвинулся на расстояние х = 10 см? (Решение)
21. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 10 5 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня? (Решение)
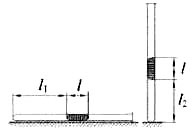
22. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23.8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. (Решение)
23. В водонепроницаемым мешок, лежащий на дне моря на глубине 73,1 м. закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и. когда объём воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикреплённым к нему грузом массой 25,0 тонн. Определите массу воздуха в мешке в момент начала его всплывания. Температура воды раина 7°С. атмосферное давление па уровне моря равно 10 5 Па. Объёмом груза и стенок мешка пренебречь. Масса оболочки мешка неизвестна. (Решение)
24. Сосуд разделен тонкой перегородкой на две части, отношение объёмов у которых V2/V1 = 3. В первой и второй частях сосуда находится воздух с относительной влажностью соответственно φ1 = 60% и φ2 = 70%. Какой будет влажность воздуха в сосуде, если перегородку убрать? Считать, что температура воздуха постоянна.(Решение)

25. В металлическом сосуде под поршнем находится воздух при атмосферном давлении (см. рисунок). Сосуд имеет массу 10 кг и расположен в горизонтальном положении на поверхности стола. Поршень может скользить без трения со стенками сосуда. Массон поршня и воздуха, заключённого в сосуде, можно пренебречь. За привязанный к нему шнур поршень очень медленно тянут в горизонтальном направлении. На сколько процентов возрастёт объём воздуха под поршнем к моменту, когда сосуд начнёт скользить по столу? Коэффициент трения покоя между сосудом и поверхностью стола равен 0,5. Площадь дна поршня 105 см 2 . Атмосферное давление 10 5 Па. (Решение)
26.Один моль одноатомного идеального газа совершает процесс 1-2-3, график которого показан на рисунке в координатах р-Т. Известно, что давление газа р в процессе 1-2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1-2-3, если его температура Т в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К? (Решение)
27. Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой - аргон. В начальный момент температура гелия равна 300 К,. а аргона - 900 К. Объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объём, занимаемый гелием, после установления теплового равновесия, если поршень перемешается без трения? Теплоёмкостью цилиндра н поршня пренебречь. (Решение)

28. Аэростат объемом V = 200 м 3 наполняют горячим воздухом при температуре t = 280 °С и нормальном атмосферном давлении. Температура окружающего воздуха t0 = 0°С. Какую максимальную массу должна иметь оболочка аэростата, чтобы он мог подниматься? Оболочка аэростата нерастяжима и имеет в нижней части небольшое отверстие. (Ответ: 129 кг)

29. Аэростат, оболочка которого имеет массу М = 200 кг и объем V = 350 м 3 , наполняют горячим воздухом при нормальном атмосферном давлении. Температура окружающего воздуха t0 = 0 °С. Какой должна быть температура воздуха внутри оболочки, чтобы он начал подниматься? Оболочка аэростата нерастяжима и имеет в нижней части небольшое отверстие. (Ответ: 220°С)
В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ
В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ. Расстояния от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего одинаковы и равны h (рис.). Давление воздуха под верхним поршнем вдвое больше атмосферного. Вся система находится в равновесии. На верхний поршень надавливают так, что он опускается на место нижнего, сжимая газ. Каким станет расстояние х от нижнего поршня до дна сосуда? Атмосферное давление постоянно.

Обозначим h расстояние от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего, х — расстояние х от нижнего поршня до дна сосуда после сжатия, ратм — атмосферное давление, р1 — давление газа под верхним поршнем, рп — давление поршня, V1 — объем воздуха под верхним поршнем вначале, S — площадь основания поршней и дна цилиндра, р2 — давление под верхним поршнем после опускания верхнего поршня на место нижнего, рс — давление силы, придавившей поршень, V2 — новый объем воздуха под верхним поршнем, р3 — давление газа под нижним поршнем до опускания верхнего, р4 — давление газа под нижним поршнем после его сжатия, Т3 — объем воздуха под нижнем поршнем после сжатия.

Закон Бойля — Мариотта применительно к газу подверхним поршнем будет выглядеть так:
Давление газа под верхним поршнем р1 при равновесии равно сумме атмосферного давления ратм и давления поршня рп:
Но по условию задачи р1 = 2ратм, поэтому 2ратм = ратм + рп, откуда
Объем воздуха под верхним поршнем вначале был равен:
После опускания верхнего поршня на место нижнего газ под ними сжался и давление под верхним поршнем стало р2. Теперь оно равно сумме давлений атмосферы ратм, поршня рп и некоторой силы, придавившей поршень, рс:

Теперь нам предстоит решить систему уравнений (6) и (11) относительно искомого расстояния х, исключив из них неизвестные давления. Давайте в этих уравнениях сначала раскроем скобки и сделаем приведение подобных членов — может, мы их при этом немного упростим. Начнем с уравнения (6)
Физика
Для идеального газа, находящегося в сосуде под поршнем , необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
- постоянным остается также количество вещества (газа):
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
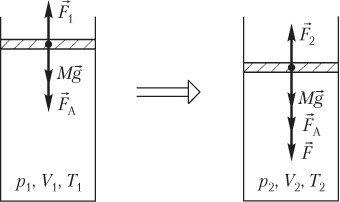
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F → (рис. 5.9).
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p 1 V 1 = ν R T 1 , p 2 V 2 = ν R T 2 , >
где p 1 , V 1 , T 1 — давление, объем и температура газа в начальном состоянии; p 2 , V 2 , T 2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
M g + F A = F 1 , M g + F A + F = F 2 , >
где M — масса поршня; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; S — площадь сечения поршня; F 1 — модуль силы давления газа на поршень в начале процесса, F 1 = p 1 S ; p 1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F 2 — модуль силы давления газа на поршень в конце процесса, F 2 = p 2 S ; p 2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
- если процесс происходит медленно, то температура газа остается постоянной –
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня , закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
- в остальных случаях поршень обладает определенной ненулевой массой —
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм 2 и массой 1,80 кг находится 360 см 3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см 3 . Температура газа при его сжатии не изменяется. Определить массу гирь.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 1 , действующая со стороны газа (до его сжатия);
- сила давления газа F → 2 , действующая со стороны газа (после его сжатия);
- m g → — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
где F 1 — модуль силы давления газа, F 1 = p 1 S ; p 1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F 2 = Mg + F A + mg ,
где F 2 — модуль силы давления газа, F 2 = p 2 S ; p 2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
где V 1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
где V 2 — объем сжатого поршнем газа.
p 1 V 1 = p 2 V 2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p 1 S = M g + p A S , p 2 S = M g + p A S + m g , p 1 V 1 = p 2 V 2 , >
которую требуется решить относительно массы гирь m .
Для этого выразим отношение давлений p 2 / p 1 из первой пары уравнений:
p 2 p 1 = M g + p A S + m g M g + p A S
и из третьего уравнения:
p 2 p 1 = V 1 V 2 ,
запишем равенство правых частей полученных отношений:
M g + p A S + m g M g + p A S = V 1 V 2 .
Отсюда следует, что искомая масса определяется формулой
m = ( M + p A S g ) ( V 1 V 2 − 1 ) .
Вычисление дает результат:
m = ( 1,80 + 100 ⋅ 10 3 ⋅ 250 ⋅ 10 − 6 10 ) ( 360 ⋅ 10 − 6 240 ⋅ 10 − 6 − 1 ) = 2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см 2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение . На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 2 , действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
где F 2 — модуль силы давления нагретого газа, F 2 = p 2 S ; p 2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
где p 1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p 1 = p A ; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
где p 2 — давление нагретого газа; T 2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
p A V = ν R T 1 , p 2 V = ν R T 2 , p 2 S = M g + p A S ; >
систему необходимо решить относительно температуры T 2 , до которой следует нагреть газ.
Для этого делением первой пары уравнений
p A V p 2 V = ν R T 1 ν R T 2
получим выражение для давления нагретого газа:
p 2 = p A T 2 T 1
и подставим его в третье уравнение системы:
p A T 2 S T 1 = M g + p A S .
Преобразуем полученное выражение к виду
T 2 = T 1 ( M g + p A S ) p A S = T 1 ( M g p A S + 1 ) ,
а затем найдем разность
Δ T = T 2 − T 1 = M g T 1 p A S .
Δ T = 1,2 ⋅ 10 ⋅ 300 100 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 36 К = 36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см 2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → , действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a → :
F → + F → A + M g → = m a → ,
или в проекции на вертикальную ось —
где F — модуль силы давления газа под поршнем, F = pS ; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a = F − F A − M g M = ( p − p A ) S M − g .
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
и подставим в записанную формулу выражение для модуля ускорения:
v = 2 l ( ( p − p A ) S M − g ) .
v = 2 ⋅ 3,75 ( ( 450 − 100 ) ⋅ 10 3 ⋅ 50 ⋅ 10 − 4 75,0 − 10 ) ≈ 10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Идеальный одноатомный газ в количестве ν = 0, 09 моль находится в равновесии в вертикальном цилиндре под поршнем массой 5 кг?
Идеальный одноатомный газ в количестве ν = 0, 09 моль находится в равновесии в вертикальном цилиндре под поршнем массой 5 кг.
Трение между поршнем и стенками цилиндра отсутствует.
Внешнее атмосферное давление равно p = 100 кПа.
В результате нагревания газа поршень поднялся на высоту Δh = 4 см, а температура газа поднялась на ΔT = 16 К.
Чему равна площадь поршня?
Закон Менделеева - Клапейрона в руки.

A = p∆V = mR∆T / M = νR∆T.
А1 = mgh поднятие
A2 = paSh «расширение»
S = (νR∆T - mgh) / pah = 0.
0025 (м ^ 2) = 25 см кв.
В вертикальном цилиндре под подвижным поршнем площадью 40 см ^ 2 находится 1 моль идеального газа при температуре 400К?
В вертикальном цилиндре под подвижным поршнем площадью 40 см ^ 2 находится 1 моль идеального газа при температуре 400К.
Определить в литрах объем газа, если масса поршня равна 40кг, а атмосферное давление 100кПа.
Трением поршня о стенки цилиндра пренебречь.
Одноатомный газ количеством 2 моль находится в цилиндре с подвижным поршнем под атмосферным давлением?
Одноатомный газ количеством 2 моль находится в цилиндре с подвижным поршнем под атмосферным давлением.
В процессе нагревания температура увеличилась от 20 °C до 70°C, объем увеличился на 40л.
Которое количество теплоты было дано газу?
В откачанном пространстве вертикально стоит цилиндрический сосуд, перекрытый сверху подвижным поршнем массыМ?
В откачанном пространстве вертикально стоит цилиндрический сосуд, перекрытый сверху подвижным поршнем массыМ.
Под поршнем находится одноатомный газ при температуре Ти давлении Р.
Внутреннее сечение цилиндра S, высота той части сосуда, в которой находится газ, Н.
Поршень отпустили, он начал двигаться.
Чему равна максимальная скорость, развиваемая поршнем, если газ сжимается адиабатически?
В вертикальном цилиндре под невесомым поршнем находится идеальный газ?
В вертикальном цилиндре под невесомым поршнем находится идеальный газ.
Поршень может скользить по стенкам сосуда без трения.
Как изменится средняя кинетическая энергия поступательного движения молекул этого газа, если уменьшить объем газа под поршнем в 2 раза.
В цилиндре под поршнем находится идеальный газ?
В цилиндре под поршнем находится идеальный газ.
Надавливая на поршень, расстояние между поршнем и дном цилиндра уменьшают на треть.
Во сколько раз изменилось давление газа, если его температура поддерживалась постоянноя?
Среднее давление газов на поршень в цилиндре двигателя трактора 5000000 Па, ход поршня 15, 2 см, площадь 120 квад?
Среднее давление газов на поршень в цилиндре двигателя трактора 5000000 Па, ход поршня 15, 2 см, площадь 120 квад.
См. Чему равна работа за один ход поршня?
Под давлением газа поршень в цилиндре равномерно переместился на 4 см?
Под давлением газа поршень в цилиндре равномерно переместился на 4 см.
Какую работу выполнил газ?
Давление газа в цилиндре постоянно и равно 0, 6 МПа ; площадь поршня равна 0, 005м квадратных.
Под поршнем, который может свободно перемищаться в вертикальном цилиндре, ноходиться 2 моля одноатомного идеального газа?
Под поршнем, который может свободно перемищаться в вертикальном цилиндре, ноходиться 2 моля одноатомного идеального газа.
Какое количество теплоты надо сообщить газу, чтобы его темпиратура поднялась на 40К».
Одинаковая ли энергия потребуется для нагревания газа до одной и той же температуры : когда он находится в цилиндре с легкоподвижным поршнем ; когда поршень закреплен?
Одинаковая ли энергия потребуется для нагревания газа до одной и той же температуры : когда он находится в цилиндре с легкоподвижным поршнем ; когда поршень закреплен.
В цилиндре закрытом легкоподвижным поршнем массой m и площадью s находится газ?
В цилиндре закрытом легкоподвижным поршнем массой m и площадью s находится газ.
Объём газа равен Vо.
Каким станет Объём газа, если цилиндр передвигать вертикально с ускорением a вверх.
Атмосферное давление равно Pо, температура газа постоянна.
На этой странице сайта вы найдете ответы на вопрос Идеальный одноатомный газ в количестве ν = 0, 09 моль находится в равновесии в вертикальном цилиндре под поршнем массой 5 кг?, относящийся к категории Физика. Сложность вопроса соответствует базовым знаниям учеников 10 - 11 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.
Масса молотка m = P / g Ek = m * V ^ 2 / 2 = P * V ^ 2 / 2 * g По закону сохранения энергии Ek = F * s P * V ^ 2 / 2 * g = F * s F = P * V ^ 2 / 2 * g * s = 4, 9 * 25 / 2 * 9, 8 * 8 * 10 ^ - 3 = 781 H.
Нет. Потому что на Земле сила притяжения сильнее, чем на луне.
T = 5 min = 300sek 20cm = 0, 002 75% примерно 3. 94 * 10 ^ - 7 0, 006 / (3, 94 * 10 ^ - 7 * 3000) = 5, 07 = 5 A.
Если Вам еще не ответили, то всему классу сообщаю : Сначала найдем массу спирта : m = ρ·V = 800 * 0, 003 = 2, 4 кг Здесь 800 кг / м³ - плотность спирта а 3 литра - это 0, 003 м³ Если испарять 2, 4 кг спирта, то для этого потребуется Q = L * m = 8, 5 ..
Равновесия, ускорение в принципе может быть равно нулю только в двух случаях : 1)Если тело находится в покое 2)Если тело движется с постоянной скоростью, равной скорости начальной.
Задачи решаются по закону Гука, который установил линейную зависимость между силой и деформацией пружины. F = - kx1) Найдем коэффициент деформации k = ΔF / Δx = (30 - 10) / (20 - 16) = 20 / 4 = 5 Н / см Пружина при нагрузке 10Н имеет длину 16см, т. ..
Пространство это там где мы находимся время это единица измерения нашей жизни.
Я Вам завтра отправлю задачу, решение готово, но проблемы с отправкой изображения.
2. 7г / см3 вот по моему так.
Po = 8900 кг / м3S = 2 * 10 ^ - 6 м2m = 17. 8 кгL = ? = = = = = = m = po * V V = S * LL = m / (po * S) = 17. 8 / (8900 * 2 * 10 ^ - 6) = 1000 м = = = = = = = = = = = = = = = = = = = =.
Уравнение состояния. Сосуды и поршни
Задача 1. В закрытом цилиндрическом сосуде находится газ при нормальных условиях. Сосуд расположен горизонтально и разделен подвижным поршнем в отношении . В каком отношении поршень будет делить сосуд, если его меньшую часть нагреть до , а большую охладить до ?
Понятно, что, раз поршень в равновесии, то давление одинаково с обеих сторон: .

Состояние газа в левой части сосуда описывается уравнением:
Его количество пропорционально величине:
Количество газа в правой части сосуда пропорционально:
После изменения температур в левой части состояние газа таково:
Возьмем отношение двух последних равенств:
То есть, подставляя и , получим:
Ответ:
Задача 2. В закрытом цилиндрическом сосуде находится газ при температуре . Внутри сосуд перегорожен легким, не проводящим тепло поршнем радиуса см на две части объемами см и см . Поршень находится в равновесии. На какое расстояние переместится поршень, если большую часть газа нагреть на 30К? Температура в другой части не меняется.
Давление изначально одинаково с обеих сторон: .
Состояние газа в левой части сосуда описывается уравнением:
А в правой части:
После того как газ нагрели, его давление и объем в обеих частях сосуда должны измениться, но по-прежнему давление слева и справа равны:
Возьмем отношение двух последних равенств:
Количество газа в меньшей части сосуда пропорционально величине:
Количество газа в правой части сосуда пропорционально:
Так как объем равен произведению , то
Но , поэтому в левой части имеем:
И, так как , то
Но нам неизвестно, поэтому вместо этой величины используем отношение :
Ответ: поршень сдвинется на 0,67 см.
Задача 3. Сосуд с газом плотно закрыт пробкой, площадь сечения которой см . До какой температуры надо нагреть газ, чтобы пробка вылетела из сосуда, если сила трения, удерживающая пробку, Н? Начальное давление воздуха в сосуде Па, начальная температура .
Газ, находящийся в сосуде, изначально оказывает давление на пробку. Только его недостаточно для того, чтобы выдавить ее. Поэтому считаем, что избыточное давление, то есть изменение давления – как раз и выдавит пробку. Тогда
А так как процесс изохорный, то
Ответ: газ надо нагреть на , то есть до температуры .
Задача 4. В цилиндрическом сосуде с газом находится в равновесии тяжелый поршень. Масса газа и температура под поршнем и над ним одинаковы. Отношение объема над поршнем к объему под поршнем равно 3. Каким будет это отношение, если температуру в сосуде увеличить в 2 раза?
Рассмотрим состояние газа до нагрева. Температура обеих частей одинакова, массы равны, то есть
При этом понятно, что давления разные в обеих частях, так как объемы не одинаковы:
Следовательно, так как , то
Аналогично и после нагрева: так как газ нагревают в обеих частях сосуда, и масса газа в обеих частях одинакова, то можно записать, что
Подставим давление поршня:
Перейдем к объемам:
Подставим эти соотношения:
Запишем объем после нагрева через приращение объема:
Перейдем к полному объему сосуда:
Теперь мы имеем всего две неизвестных в одном уравнении, и можем разделить все уравнение, например, на :
Задание 12. МКТ, термодинамика. Установление соответствия . ЕГЭ 2022 по физике

С некоторой массой идеального газа был проведён циклический процесс, изображённый на рисунке. Укажите, как менялся объём газа при переходе из 1 → 2 и 4 → 1. Для каждого случая определите соответствующий характер изменения:
| Процессы | Характер изменения |
| A) Процесс 1 → 2 Б) Процесс 4 → 1 | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждого процесса. Цифры в ответе могут повторяться.
Решение
В процессе 1-2 объем газа не менялся, т.к. переход 1-2 - это изохора, покольку его продолжение идет через начало координат. Переход 4-1 - изобара, т.к. $p_1=p_4$, тогда $
Задача 10
В сосуде объёмом V при давлении p и температуре T находится идеальный газ массой m и молярной массой M . Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физические явления | Формулы |
| А) давление газа Б) температура газа | 1) $ 2) $ 3) $ 4) $ |
Решение
Из формул и формулировок МКТ очевидно, что $P=
Задача 11
По мере понижения температуры воды от +40◦С до −20◦С она находилась сначала в жидком состоянии, затем происходил процесс её отвердевания и дальнейшее охлаждение твёрдой фазы воды–льда. Изменялась ли внутренняя энергия воды во время этих процессов и если изменялась, то как? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Отвердевание воды Б) Охлаждение льда | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
1) Отвердевание воды и охлаждение льда два процесса, подчиняющихся первому началу термодинамики, согласно которому внутренняя энергия изменяется при совершении работы или передачи тепла. Следовательно, внутренняя энергия воды уменьшилась в ходе всех двух процессов.
Задача 12
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит шарик. Из сосуда выпускается половина газа при неизменной температуре. Как изменились в результате этого объём газа и действующая на шарик архимедова сила? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Объём газа Б) Архимедова сила | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если у сосуда выпустить половину газа, то атмосферное давление уравновесит давление поршнем и поршень передвинется вниз, вследствие чего, объем газа уменьшится. Архимедова же сила, действующая на шарик, не изменится, поскольку плотность газа под поршнем останется неизменной: $F_<арх>=p_г·g·V_ш$, где $g=9.8м/с^2$ - ускорение свободного падения, $V_ш$ - объем шарика, $p_г$ - плотность газа под поршнем.
Задача 13
Температуру нагревателя тепловой машины уменьшили, оставив температуру холодильника прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и количество теплоты, отданное газом за цикл холодильнику? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) КПД тепловой машины Б) Количество теплоты, отданное газом за цикл холодильнику | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если понизить температуру нагревателя при неизменной температуре холодильника, то КПД идеальной тепловой машины уменьшается в соответствие с уравнением: $η=(1-
Задача 14
Если налить воду в открытый сосуд, то она начнёт испаряться. Как будут меняться при этом её температура и внутренняя энергия? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
При испарении, жидкость покидают наиболее быстрые молекулы, поэтому средняя скорость остальных молекул жидкости становится меньше. Следовательно, и средняя кинетическая энергия остающихся в жидкости молекул уменьшается. Это означает, что температура жидкости и внутренняя энергия испаряющейся жидкости уменьшается.
Задача 15
Ученик наблюдает за процессом кипения воды, нагреваемой в кастрюле на электроплите. Как в процессе кипения меняется температура и внутренняя энергия системы «вода–пар»? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
При кипении, температура системы "вода-пар" остается постоянной, а внутренняя энергия данной системы увеличивается, т.к. происходит поглощение тепловой энергии.
Задача 16
В вертикальном цилиндрическом сосуде под поршнем, способным перемещаться без трения, находится воздух.Как изменятся температура газа и его объём, если поршень быстро сместить вниз? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Объём | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если поршень быстро сместить вниз, то объем газа уменьшится, давление - увеличится, а так как давление связано с температурой соотношением: $p=nkT$, то и температура тоже увеличится.
Задача 17
В вертикальном цилиндрическом сосуде под поршнем, способным перемещаться без трения, находится воздух. Как изменятся давление газа и его внутренняя энергия, если поршень быстро сместить вверх? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Давление Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если поршень сместить вверх, то обмен с окружающейс средой произойти не успеет - процесс будет адиабатным. Тогда из 1 закона термодинамики $Q=0=A+∆U$, тогда $∆U=-A$. Газ расширяется, значит $A>0$, следовательно, и $∆U T_1$, то при повышении температуры воздуха скорость его молекул увеличится, это приведет к увеличению ударов молекул о стенки сосуда и поршня, а следовательно, к увеличению давления, что приведет к тому, что поршень сместится, увеличив объем газа, плотность же газа, уменьшится, поскольку $p=
Читайте также: