В данных изображениях определи вид симметрии осевая центральная или обе знак мерседеса
Задача: Осевая симметрия
Легко проверить, что множество точек осесимметрично относительно оси X (или Y - тогда рассуждения те же, но относительно другой оси).
Предположим, что ось симметрии существует. Тогда её можно поворотом на угол phi перевести в ось X.
При этом координаты точек преобразуются так:
x' = x cos phi + y sin phi
y' = -x sin phi + y cos phi
Если множество осесимметрично относительно оси X, то сумма y-координат будет равна 0. Отсюда
tg phi = X/Y,
где X - сумма x-координат исходных точек, а Y - сумма y-координат исходных точек.
Поворачиваем множество исходных точек на этот угол - и проверяем, симметрично ли оно относительно оси X.
(1) А обратное и не нужно. Это необходимое условия. _После_ преобразования - проверка.
Насчёт выбора угла - просто подставь, затем вынеси sin и cos за скобки.
(9) Дают. И даже очень часто :-(
Тогда есть такой вариант: "центрируем" множество точек, вычитая из каждого радиус-вектора 1/n \Sigms r_k, где r_k - радиус-векторы точек.
Находим точки с максимальным расстоянием до центра.
(Возможная) ось симметрии будет проходить либо через центр и одну из "максимальных" точек, либо через центр и середину отрезка между двумя "максимальными" точками.
Проверяем все возможные оси.
Перебором, конечно, неприятно - но хоть какой-то вариант.
Частный вариант если точки не лежат на оси симметрии:
Допустим точек всего N. Тогда условие симметрии соблюдается тогда, если можно разбить N на такие пары, что мат среднее координат каждой пары Xср = (X1 + X2)/2, Yср = (Y1+Y2)/2 (короче говоря точка посередине) удовлетворяет уравнению У
= KX + H; K и H находятся для первых двух пар.
Количество проверок равно кол-во сочетаний из N по 2 (т.е каждую точку с каждой другой). Таких будет N!/2!(N-2)! = N(N-1)/2
Для случаев когда есть точки на оси просто дубируем в массив каждую точку и проверяем, всего проверок тогда будет N(2N-1)
Что имеется в виду под проверкой на симметрию в этом случае?
(21) Ну да, сорри, верно определяет только отсутствие симметрии у всех точек, для полной проверки надо дальше проверять (отбросим эти и дальше аналогично).
Осевая и центральная симметрия

В природе симметрия встречается очень часто. Ее можно наблюдать в расположении органов у животных, в строении листьев и цветов растений, во взмахе крыльев, одним словом везде. А человек взял на вооружение этот инструмент, и использует его и в проектировании сложных объектов, и в искусстве, а так же в других сферах деятельности. Различают осевую и центральную симметрию, а чтобы разобраться какая между ними разница, надо изучить рисунки из этой статьи.
Осевая симметрия. 
Рисунок яблока в симметрии. 
У равностороннего треугольника три оси симметрии. 
На тетрадном листочке. 
Зеркальное отражение. 
Квадрат имеет четыре оси симметрии. 
Центральная симметрия в квадратах. 
Ось симметрии в творчестве. 
Осевая симметрия. 
Относительно одной точки. Все отрезки равны. 
Симметрия относительно прямой. 
В художестве. 
Презентация на тему: «Осевая и центральная симметрия»
МБОУ СОШ п. Солидарность Презентация на тему: «Осевая и центральная симметрия» подготовила Пономарева Елизавета ученица 8 «А» класса 2017 г.
«Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство» Герман Вейль
В древности слово «СИММЕТРИЯ» употреблялось в значении «гармония», «красота». В переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей»
Виды Центральная симметрия Осевая симметрия
Точки А и А 1 называются симметричными относительно прямой а , если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему. а А А 1 а – ось симметрии Р М М 1 b N N 1 Точка Р симметрична самой себе относительно прямой b Осевая симметрия
Симметричность относительно прямой
У прямоугольника 2 оси симметрии
А вот у круга бесконечно много осей симметрии, все они являются диаметрами
У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть совсем. Мысленно определите, сколько осей симметрии имеет каждая из фигур?
У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть совсем. Мысленно определите, сколько осей симметрии имеет каждая из фигур?
Центральная симметрия Точки А 1 и А 2 называются симметричными относительно точки О, если О – середина отрезка А 1 А 2 А 1 А 2 О О Р Q M M 1 N N 1 А 1 О = ОА 2 Точка О – центр симметрии
Центральная симметрия А В С А 1 С 1 А В С О С 1 А 1 В 1
Примерами фигур, обладающих центральной симметрией , являются окружность и параллелограмм Параллелограмм Окружность о О
A A 1 B 1 B C C 1 Симметричность на координатной плоскости y y x x A B C D A 1 B 1 C 1 D 1 y x x A B C D A 1 B 1 C 1 D 1
Фигуры, обладающие центральной и осевой симметрией О В А L N D С Фигура называется симметричной относительно точки О , если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Фигура называется симметричной относительно прямой а , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. К М E P b T Q
Фигуры, не обладающие свойством симметрии
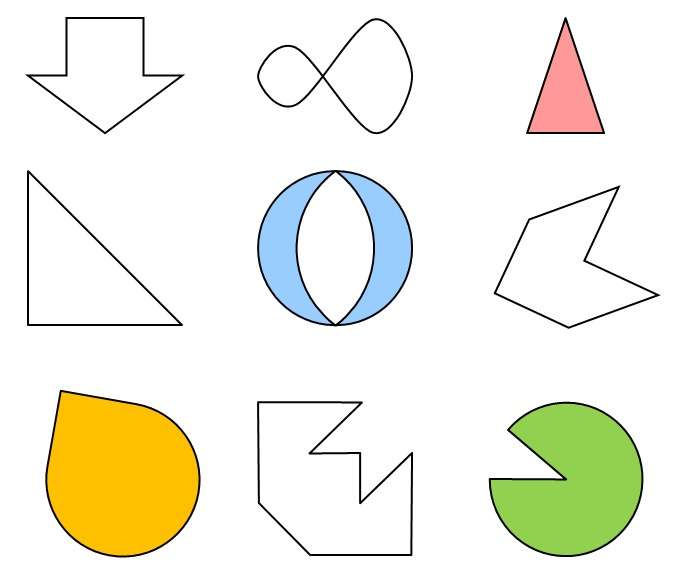
Определить фигуры: обладающие центральной симметрией и указать их центр ; обладающие осевой симметрией и указать ось симметрии; имеющие обе симметрии.
Фигуры, обладающие центральной симметрией Фигуры, обладающие осевой симметрией Фигуры, имеющие обе симметрии
Осевая симметрия: звери и птицы
Центральную симметрию использовали мастерицы по бисеру для украшения одежды.
Осевая симметрия
- Осева́я симме́три́я — тип симметрии, имеющий несколько отличающихся определений:
Отражательная симметрия. В евклидовой геометрии осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Отсюда следует, что любой точке соответствует точка, находящаяся на том же расстоянии от оси симметрии, и лежащая на одной прямой с исходной точкой и их общей проекцией на ось симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две диагонали — в плоскости фигуры; если это не квадрат с двумя дополнительными осями — медиатрисами сторон), а параллелограмм общего вида имеет одну ось симметрии (проходящую через центр перпендикулярно плоскости).
Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию (другие термины — радиальная, аксиальная (англ. axial – осевой), поворотная, лучевая симметрии) относительно поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но, например, конус будет.Применительно к плоскости эти два вида симметрии совпадают (считаем, что ось тоже принадлежит этой плоскости).
В кристаллографии вводят также (осевую) симметрию некоторого порядка:
Осевая симметрия n-го порядка — симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси. Описывается группой Zn.
* Тогда симметрия в первом смысле (см. выше) является осевой симметрией второго порядка, а во втором — ∞-го порядка, так как поворот на любой сколь угодно малый угол приводит к совмещению фигуры с самой собой. Примеры: шар, цилиндр, конус.
* Оси симметрии 2-го, 3-го, 4-го, 6-го и даже 5-го порядка (кристаллы с непериодическим пространственным расположением атомов (мозаика Пенроуза)) можно наблюдать на примере кристаллов.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Кристаллографические группы, или фёдоровские группы — набор групп симметрий, которые описывают все возможные симметрии бесконечного количества периодически расположенных точек в трёхмерном пространстве.
В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.
В статье суммируется информация о классах дискретных групп симметрии евклидовой плоскости. Группы симметрии, приведённые здесь, именуются по трём схемам именования: междурародная нотация, орбифолдная нотация и нотация Коксетера.
Существует два определения хирального многогранника. По одному определению — это многогранник в прямом смысле хиральности (или "зеркальной симметричности"), то есть, что многогранник не имеет зеркальной симметрии. По этому определению многогранник, у которого отсутствует любая симметрия, вообще будет примером хирального многогранника.
Основное свойство проективной плоскости — «симметрия» ролей, которые играют точки и прямые в определениях и теоремах, и двойственность является формализацией этой концепции. Имеются два подхода к этой двойственности: один, использующий язык (см. «принцип двойственности» ниже), и другой, более функциональный подход. Они полностью эквивалентны и оба служат исходной точкой для аксиоматических версий геометрии. В функциональном подходе имеется соответствие между геометриями, которое называется двойственностью.
Симметрия является неотъемлемой частью мира, в котором мы живем. Мы восхищаемся красотой природы, архитектурными сооружениями, механическими приборами и шедеврами искусства, не задумываясь над тем, что в основе их создания лежит симметрия.
«Симметрия» с греческого языка переводится как гармония, соразмерность, красота. Впервые термин стал широко употреблять Пифагор в до н.э. Им он обозначил трехмерное изображение геометрических фигур и их частей в пространстве. Также ученый определил отклонение от симметрии как асимметрию.
Существует два основных виды симметрии: осевая и центральная.
Осевая симметрия или зеркальная – это симметрия относительно оси. То есть одна половинка фигуры полностью соразмерна с другой относительно прямой. Так если согнуть листок пополам, то каждая точка одной половины листа будет иметь своего двойника на другой половине, а сам сгиб станет осью симметрии.
Зеркальную симметрию можно наблюдать в природе: листья растений симметричны относительно среднего стебля, крылья бабочки являются зеркальным отображением друг друга, человек и животные обладают симметрией в расположении частей тела. Архитектурные сооружения также являются ярким примером осевой симметрии. Фасады зданий, особенно античных, вызывают чувства строгости и восхищения красотой именно благодаря симметрии их частей. Симметрия в архитектуре служит не только для эстетического удовольствия наблюдателей, но и гарантирует зданиям и сооружениям прочность и надежность конструкции.
Центральная симметрия – это симметрия относительно точки. У такой симметрии обязательно есть неподвижный центр, при вращательных действиях на 180° относительно него фигура переходит сама в себя. Благодаря этому свойству центральная симметрия получила второе название – поворотная. С древнейших времен ее эталоном считается круг, и действительно, как бы мы не поворачивали его вокруг центра, каждая точка окружности переходит в соответствующую ей. В природе ярким примером центральной симметрии являются снежинки; цветы таких растений, как одуванчик, мать-и-мачеха, а также ромашки, если количество ее лепестков четное; шестеренки механизмов.
Вариант 2
Наверное, каждый слышал такие понятия, как "симметрия", "симметрично" и тому подобное. Но есть такие люди, которые не понимают значение данных синонимов. Так что же такое симметрия? Где ее применяют? И какие разновидности существуют?
Краткий экскурс о симметрии в общих чертах.
Постараюсь объяснить понятие симметрии на некотором примере. Представьте обыкновенную бабочку. Так, а теперь надо провести через нее линию. Когда линия окончательно проведена, необходимо посмотреть на правую и левую части рисунка. Если эти 2 части рисунка одинаковы по размерам и пропорциям, то это можно называть симметричной моделью. Короче говоря, симметрия – это полная соразмерность частей тела по отношению к линии. Где же применяется симметрия? Ну, симметрия встречается везде, где только можно. Геометрия, физика, биология, химия, культура – все это содержит симметрию, причем каждая отличается друг от друга. Еще существует понятие асимметрии. То есть, отсутствие правильной соразмерности. Еще стоит отметить, что симметрия не всегда бывает точной.
Некоторые виды симметрии, их характеристика и применение.
Всего наберется с десяток разных видов симметрий. Но рассмотреть необходимо только те, которые часто встречаются. Сразу стоит сказать, что обе из них находят применение в решении задач по геометрии. Итак, вот 2 главных вида симметрии:
Осевая симметрия.
Этот вид симметрии делится на 4 группы, отличающиеся друг от друга.
1) Отражательная симметрия – это зеркальное движение, в котором точки, не перемещающиеся никуда, соединены в одну линию – ось симметрии. Прямоугольник и параллелограмм – отличные примеры.
2) Вращательная симметрия – это осевая симметрия, которая относительна поворотам вокруг оси.
3) Осевая симметрия n – го порядка – это симметрия относительно поворотов на 360 градусов вокруг оси.
4) Зеркально поворотная осевая симметрия n – го порядка – то же самое, только перпендикулярно оси.
Центральная симметрия.
Это преобразование, при котором каждая точка А переходит в точку А1, при этом она симметрична предыдущей относительно оси О. Данная симметрия – это, по сути, тот же поворот на 180 градусов в планиметрии. Центральную симметрию от осевой отличает то, что в первом случае присутствует движение.

Популярные сегодня темы
Одно из самых загадочных всемирно известных построений древних лет, которое, по мнению многих историков, скульпторов, архитекторов, обладает душой, считается Собор Парижской Богоматери. Этот
Блохи относятся к бескрылым паразитирующим насекомым. Паразитируют блохи на птицах, животных и некоторые виды на человеке.
Сказка «Конек – Горбунок», наверное, неизвестна лишь тем, кто не воспитывался и не рос в России и на всем постсоветском пространстве. Для всех остальных она является одним из теплых воспомин
Профессиональный спорт появился относительно недавно, хотя как часть культуры спорт существует со времен зарождения цивилизаций. Многие знают истории об играх в ацтекской цивилизации, где спо
Родиной герани является южная часть Африки. Ученым известно более 300 видов пеларгонии (научное название герани). Это кустарниковые, травянистые и ползущие растения. В Европе она появилась в
Календарь представляет собой систему организованных единиц времени для расчета времени за прошедшие периоды. Условно, день является наименьшей календарной единицей времени.
Ось симметрии - что это такое? Фигуры, имеющие ось симметрии
Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, - точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.
Симметрия
Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия - свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.

Вам будет интересно: Как сдать физику и что нужно для этого сделать?
Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Виды симметрии
Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:
История симметрии
Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.
В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то "центрального огня", вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.
А философ Платон считал многогранники олицетворением четырех природных стихий:
- тетраэдр - огонь, так как его вершина направлена вверх;
- куб - земля, так как это самое устойчивое тело;
- октаэдр - воздух, нет каких-либо объяснений;
- икосаэдр - вода, так как тело не имеет грубых геометрических форм, углов и так далее;
- образом всей Вселенной являлся додекаэдр.
Из-за всех этих теорий правильные многогранники называют телами Платона.
Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины "День и ночь".
Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. "Богатыри".
Что уж там говорить, симметрия - ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника - также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно - длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.
Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых - бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии - диагонали, а во втором - средние линии. Множество таковых осей только у квадрата.
Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия - основное условие.
Вывод
Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия - очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием "симметрия" понимают регулярную смену дня и ночи, времен года и так далее.

Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы - астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия - один из основополагающих законов мироздания в целом.
Осевая и центральная симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, у которых есть ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу квадрат, треугольник и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот, как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на прямой.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника с осевой симметрией.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Измеряем расстояние от точки B до прямой l и от точки A до прямой l.
- Проводим прямую от точки А через прямую l, выводя за ось симметрии.
- Проводим прямую от точки B через прямую l, выводя за ось симметрии.
- Соединяем точки отрезка A1B1.
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Постройте треугольник A1B1C1, симметричный треугольнику ABC, относительно центра (точки О).
- По аналогии с предыдущим примером сначала соединяем точки ABC с точкой O.
- Выводим отрезки за точку О.
- Измеряем отрезки AO, BO, CO и чертим такие же на противоположной стороне.
- Получаем два центрально-симметричных треугольника.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки равные отрезкам АО и АB.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1 N1.

Подсказка: опустите перпендикуляры из точки N и N1 на прямую MМ1
Задачка 2. Постройте фигуру, симметричную данной относительно оси a.
Определите виды симметрии у данных животных
Размеры: 498 х 214 пикселей, формат: png. Чтобы бесплатно скачать картинку для урока геометрии щёлкните по изображению правой кнопкой мышки и нажмите «Сохранить изображение как. ». Для показа картинок на уроке Вы также можете бесплатно скачать презентацию «Симметрия.ppt» целиком со всеми картинками в zip-архиве. Размер архива - 9467 КБ.
Похожие презентации
«Движение симметрия» - Как построить точку симметричную данной относительно некоторой точки О? Понятие движения. Какими общими свойствами обладают осевая и центральная симметрия? В таком случае говорят, что дано отображение плоскости на себя. Отображение плоскости на себя, сохраняющее расстояние, называют – движением. Как построить точку симметричную данной относительно прямой L?
«8 класс симметрия» - С тобою в дружбе и тюльпан, и роза, и снежный рой-творение мороза! Какие геометрические фигуры имеют ось симметрии? Какие прямые называются перпендикулярными? Какие прямые называются параллельными? Каково взаимное расположение прямых на плоскости? Изучение нового материала. «Симметрия относительно прямой» и «Класс насекомых».
«Симметрия в природе» - В 19 веке, в Европе, появились единичные работы, посвящённые симметрии растений. Симметрия в природе и в жизни. Греческое слово симметрия буквально обозначает «соразмерность». Учение о различных видах симметрии представляет большую и важную ветвь геометрии, тесно связанную со многими отраслями естествознания и техники, начиная от текстильного производства и кончая тонкими вопросами строения вещества.
«Симметрия правильных многогранников» - Венеция. 1509. Что такое симметрия? Правильный додекаэдр. Кристаллы льда. составлен из шести квадратов. составлен из четырех равносторонних треугольников. Микеланджело. Следовательно, сумма плоских углов при каждой вершине равна 270°. Элементы симметрии: Гробница Джулиано Медичи. Поэтому правильные многогранники также называются платоновыми телами.
«Осевая симметрия 8 класс» - Какие буквы имеют ось симметрии ? Осевая симметрия в природе. 2.Докажите, что преобразование обратное осевой симметрии является осевой симметрией. Осевая симметрия в архитектуре. Ось симметрии. Осевая симметрия. Сколько осей симметрии имеет каждая из геометрических фигур? L-ось симметрии.
«Осевая и центральная симметрия» - Прямая а называется осью симметрии фигуры. Центральная симметрия. Точка О – центр симметрии фигуры. Отрезок, луч, пара пересекающихся прямых, квадрат? Достроить фигуру, обладающую центральной симметрией. Достроить правую часть фигуры, симметричной относительно прямой а. Симметрия относительно точки.
В данных изображениях определи вид симметрии осевая центральная или обе знак мерседеса
Можно установить далеко идущую аналогию в свойствах инверсии и осевой симметрии. Для этого напомним некоторые свойства инверсии.
1. Инверсия сохраняет угол переоечения двух линий, меняя при этом его ориентацию.
2. Прямая, ортогональная базисной окружности, преобразуется в себя.
3. Базисная окружность инверсии преобразуется в себя.
4. Всякая окружность, ортогональная базисной, преобразуется в себя.
5. Всякая окружность или прямая преобразуется в окружность или прямую.
6. Две точки тогда и только тогда инверсны относительно некоторой базисной окружности, если они являются вершинами пучка окружностей, ортогональных к базисной.
Если в этих предложениях слово "инверсия" заменить словами "осевая симметрия", выражение "базисная окружность" — через "ось симметрии" и "инверсные точки" — через "симметричные точки", то получим свойства осевой симметрии.
Покажем, что в известном смысле осевую симметрию можно рассматривать как предельный случай инверсии.
Пусть базисная окружность инверсии проходит через Точку А (рис. 165), так что Обозначим через касательную
к окружности в точке А. Пусть, далее, некоторая данная точка, инверсная ей точка относительно окружности Представим себе, что центр инверсии неограниченно удаляется от точки А вдоль луча так что радиус инверсии неограниченно возрастает.
В известном смысле мозкно говорить, что при этом окружность неограниченно приближается к прямой а, "вырождается" в эту прямую. Оказывается, что при этом точка будет перемещаться по плоскости, неограниченно приближаясь к точке симметричной с точкой относительно прямой а. Докажем это.
Для определённости положим, что точка и точка О лежат по разные стороны от прямой а (рис. 165). Опустим из точки перпендикуляр на прямую а и перпендикуляр на прямую Пусть Из точки инверсной точке относительно окружности также опустим перпендикуляры и на прямые Нам нужно показать, что если Действительно,
Отсюда видно, что когда С другой стороны,
Отсюда ясно, что когда
Изложенные здесь соображения показывают, что целесообразно расширить понятие об инверсии так, чтобы можно было рассматривать осевую симметрию как специальный случай инверсии. Для этого условимся называть "окружностью в широком смысле слова" любую окружность и любую прямую. Тогда можно оба преобразования — инверсию и симметрию относительно прямой — объединить в одно понятие с помощью следующего определения. Точка называется обратной точке (или сопряжённой точке относительно окружности (в широком смысле) если точки являются вершинами пучка окружностей, ортогональных к Такое преобразование, при котором каждой точке сопоставляется сопряжённая ей точка относительно окружности (в широком смысле) назовём отражением от окружности В том случае, когда является окружностью в узком (обычном) смысле, наше преобразование представляет инверсию относительно Если же прямая, то рассматриваемое преобразование является симметрией относительно этой прямой.
Читайте также:

