Тепловая машина использующая идеальный одноатомный газ работает по замкнутому циклу
Тепловые машины. КПД
Образовательные цели урока: повторение графиков изопроцессов, закрепление умений чтения графиков изопроцессов и решения задач на первый закон термодинамики, формирование умений определять КПД тепловой машины по графику и общеучебных навыков (работы с текстом, выделения главного, преобразования информации из одного вида в другой).
Методы: эвристическая беседа, самостоятельная работа, дифференциация.
Оборудование: распечатанные для каждого ученика условие задачи и решение (вариант А), распечатанные на каждую парту условия задач различного уровня сложности для самостоятельной работы. (Возможно использование интерактивной доски.)
Ход урока
1. Организационный этап
2. Индуктор. На доске написан вариант А решения задачи. Учитель утверждает, что с таким сложным решением трудно разобраться, его невозможно запомнить. Что же делать? Для облегчения работы каждому ученику выдаётся вариант B решения задачи – копия А, но с пропусками.
3. Осмысление. Учащиеся предлагают разбить решение на логически завершённые части. Учитель обращает их внимание на сложные места в решении, причём не даёт объяснение, а только спрашивает: для чего эта запись? почему записано именно так? В результате работы текст решения превращается из первоначального варианта А в вариант с дополнениями В.
Задача
• Тепловая машина, рабочим телом которой является идеальный одноатомный газ, работает по циклу 1–2–3–1. Найдите КПД этой машины.
Исходный вариант решения (А, записан на доске).
Вариант решения B с дополнениями, написанными учениками в своих экземплярах и на доске в ходе урока. (Дополнения выделены другим шрифтом и цветом. Условие здесь не повторено. – Ред.)
Учитель предлагает применить полученные знания для решения подобной задачи или повторить решение этой же задачи. Каждый ученик выбирает для себя способ подсказки: глядя только на часть решённой задачи, восстановить всё решение; никуда не глядя, восстановить всё решение; глядя в решение, решить новую подобную задачу; решить задачу повышенного уровня сложности. Ученики выполняют самостоятельную работу.
Задачи для самостоятельного решения
• 1 моль идеального одноатомного газа совершает цикл, изображённый на рисунке, в координатах p, U, где p – давление, U – внутренняя энергия газа. Определите КПД цикла. (Ответ. КПД = 2/13 ≈ 15%.)
• Докажите, что КПД тепловой машины, работающей по циклу из двух изотерм и двух изохор, меньше КПД идеальной тепловой машины, работающей по циклу Карно, с тем же нагревателем и холодильником.
• КПД тепловой машины, работающей по циклу, состоящему из изотермы 1–2, изохоры 2–3, адиабаты 3–1, равен η, разность между максимальной и минимальной температурами газа в цикле равна ∆T. Найдите работу, совершённую ν молями одноатомного идеального газа в изотермическом процессе. (Ответ. )
• Найдите КПД тепловой машины, работающей по циклам 1–2–3–1; 1–3–4–1. рабочим телом является одноатомный идеальный газ. (Ответ. КПД = 2/23 ≈ 8,7%; КПД = 2/21 ≈ 9,5%.)
• Найдите КПД тепловой машины, работающей по циклам 1–2–3–4–1. рабочим телом является молекулярный водород. (Ответ. КПД = 6/43 ≈ 14%.)
4. Рефлексия. Школьники пишут эссе – своё мнение о значении проверки в решении задачи. Желающие зачитывают вслух.
5. ДЗ. Напишите алгоритм решения задачи и свои рекомендации своим отсутствовавшим товарищам.
Гелий – одноатомный газ, и для него
Решение.
Так как газ получает тепло от нагревателя лишь на участке 1-2,
Подставляя эти выражения, получим A = А12=3/2 RDТ/(1-h).
5. К идеальному одноатомному газу, заключенному внутри масляного пузыря, подводится тепло. Найти молярную теплоемкость этого газа, если давлением снаружи можно пренебречь. ( МФТИ, до1992г)
Ответ: С = 3R
Решение.
Воспользуемся 1-ым началом термодинамики:
Если радиус пузыря r , давление газа в пузыре по формуле Лапласа равно
объем газа V = 4/3pr 3 , так что
Для одноатомного газа
PV =RT т.е. (4s/r)(4/3pr 3 ) = RT
Изменяя r на малую величину и пренебрегая членом с (Dr) 2 , получаем, что 32/3psrDr = RDT ,
Подставляя это соотношение в первое начало, получаем
С = Сv + (4s/r) 4pr 2 3R/(32psr) = Сv + 3/2R = 3R
6. Два сосуда заполнены одним и тем же идеальным газом и сообщаются при помощи узкой трубки. Отношение объемов сосудов V1/V2 = 2 . Первоначально газ в первом сосуде имел температуру Т1 = 300К. В результате перемешивания происходит выравнивание температур. Найти первоначальную температуру газа во втором сосуде, если конечная температура Т = 350К. Теплообменом газов со стенками сосудов и трубки пренебречь.
Ответ: Т2 = 525К.
Решение.
Система, состоящая из газов в обоих сосудах, работы над другими телами не производит и теплом с окружающими телами не обменивается. Следовательно, внутренняя энергия системы сохраняется:
Подставив эти выражения в первое уравнение, получим после упрощений
Решение.
Рассмотрим систему из двух газов. Оба газа двухатомные. У них постоянная теплоемкость при постоянном объеме Сv . Система из двух газов тепла от других тел не получает и работы над телами, не входящими в систему, не совершает. Поэтому внутренняя энергия системы сохраняется:
Отсюда температура смеси
Решение.
Удельная теплоемкость в данном процессе
По первому закону термодинамики

Ответ: m = 22г.
Решение.
При конденсации пара массой m при 100 о С выделяется количество теплоты
При охлаждении получившейся воды до t = 40 o C выделяется количество теплоты
При нагревании льда от t1 = -10 o C до to = 0 o C поглощается количество теплоты
При плавлении льда поглощается количество теплоты
При нагревании получившейся воды от to до t поглощается количество теплоты
Для нагревания калориметра от t1 до t требуется количество теплоты
По закону сохранения энергии
Решение.
По определению КПД тепловой машины
где АП – полная работа газа за цикл (площадь цикла в координатах P,V), а QH – тепло, получаемое рабочим газом извне (от нагревателя). Согласно первому началу термодинамики работа на адиабате 1-2
Работа на изотерме по условию А23 = -А, работа на изохоре А31 = 0. Таким образом, полная работа газа за цикл равна
т.к. Т1 и Т2 и есть максимальная и минимальная температуры в цикле. Итак,
т.к. Сv = 3/2R (газ одноатомный).
11. Над идеальным газом постоянной массы проводится циклический процесс, состоящий из двух изобар и двух изохор, как показано на рисунке. Заданы значения давлений Р1 и Р2 и температуры Т2. При каком соотношении температур Т2 и Т4 полная работа за цикл больше: в случае Т4 > Т2 или Т4 < Т2 ?(МГУ,1999)
Решение.
Работа за цикл равна
Из уравнения Клапейрона-Менделеева:
Следовательно, работа за цикл будет больше, если Т4 > T2.
P 2 ) от начального значения Т1 = 300К до конечного
Т2 = 400К. Определить работу, совершаемую газом в этом процессе, и количество подведенного к нему тепла.
Решение.
Нарисуем график процесса в координатах Р, V. Из уравнения состояния идеального газа
где k = const, получаем
т.е. уравнение прямой, проходящей через начало координат. Работа газа равна заштрихованной площади трапеции:
Количество тепла найдем из первого закона термодинамики:
Решение.
Нарисуем цикл в координатах Р, V (см. рис.);
минимальная температура – T1, максимальная Т3 ,
Работа за цикл равна площади цикла
Решение.
Уравнение состояния газа запишется в виде
Подставляя полученные соотношение в первое начало термодинамики, запишем
15. Моль идеального газа нагревается при постоянном давлении, а затем при постоянном объеме переводится в состояние с температурой, равной начальной То = 300К. Оказалось, что в итоге газу сообщено количество теплоты Q = 5кДж. Во сколько раз изменился объем, занимаемый газом?
Ответ: n = Q/RTo + 1
Решение.
Нарисуем график процесса в координатах
P – V (см. рис.). Пусть конечный объем равен nVo. Тогда, т.к. 1 – 2 – изобара, температура в точке 2 равна nTo.
Ответ: Т2 = 312.8К
Решение.
Вычитая из второго уравнения первое, получим
Решение.
Работу, совершенную паровой машиной можно определить как
где N – мощность машины. Паровая машина отдает количество теплоты
где m – масса сгоревшего угля. Тогда
КПД идеальной тепловой машины, работающей по циклу Карно
Решение.
КПД реального теплового двигателя определяет формула
где Q1 – количество теплоты, переданной нагревателем рабочему веществу в процессе его изохорного нагревания, которому соответствует участок 1 – 2, Q2 – количество теплоты, переданной газом холодильнику в процессе его изохорного охлаждения, чему соответствует участок 3 – 4. При изохорных процессах работа А = 0, тогда согласно первому закону термодинамики
где в соответствии с уравнением Менделеева-Клайперона при изохорных процессах
Максимальный КПД идеального теплового двигателя определяется формулой
где Т1 – абсолютная температура нагревателя, Т2 – абсолютная температура холодильника. Если в состоянии 2 газ находится в тепловом равновесии с нагревателем, то его температура в этом состоянии равна температуре нагревателя Т1 . Аналогично, если в состоянии 4 газ оказался в тепловом равновесии с холодильником, то его температура в этом состоянии равна температуре холодильника Т2 , т.е. в состоянии 4 температура газа стала равна Т2. Для нахождения температур Т1 и Т2 воспользуемся уравнением Менделеева-Клайперона, применив его к состояниям газа 2 и 4:
После этого для КПД идеального двигателя получим
19. В горизонтальном неподвижном цилиндрическом сосуде, закрытом поршнем, площадь сечения которого равна S, находится один моль газа при температуре То и давлении Ро (см. рис.). Внешнее давление постоянно и равно Ро. Газ нагревают внешним источником теплоты. Поршень начинает двигаться, причем сила трения скольжения равна f. Найти зависимость температуры газа Т от получаемого им от внешнего источника количества теплоты, если в газ поступает еще и половина количества теплоты, выделяющегося при трении поршня о стенки сосуда. Построить график этой зависимости. Внутренняя энергия одного моля газа U = cT. Теплоемкостью сосуда и поршня пренебречь. (Меледин, 2.65)
Решение.
Пока поршень покоится, вся теплота идет на нагрев газа:
Найдем, используя условие равновесия и закон Шарля, критическую температуру Ткр, при превышении которой поршень начнет двигаться:
Рассчитайте КПД тепловой машины, использующей в качестве рабочего тела одноатомный идеальный газ и работающей по циклу, изображенному на рисунке?
Рассчитайте КПД тепловой машины, использующей в качестве рабочего тела одноатомный идеальный газ и работающей по циклу, изображенному на рисунке.
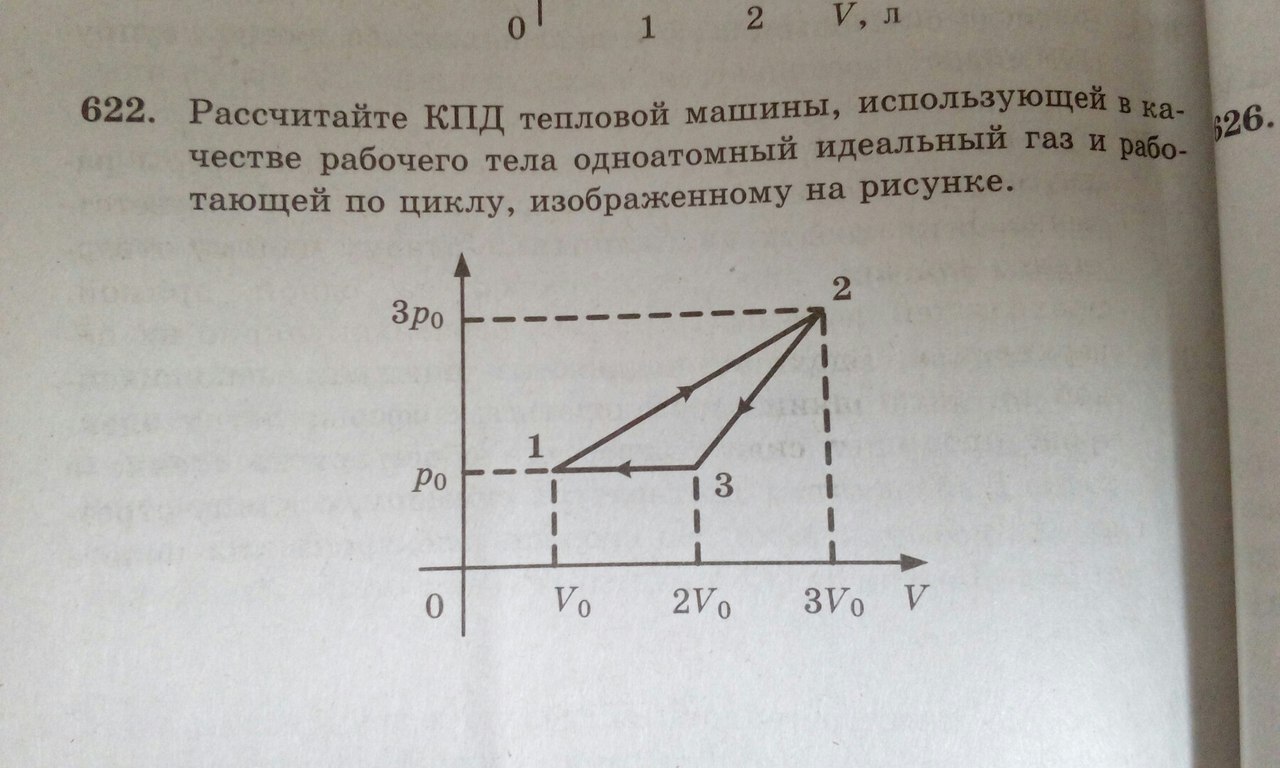
• КПД равен отношению работы газа к количеству теплоты от нагревателя, которое он получил за весь процесс :
• работа газа складывается из всех участков на диаграмме :
○ Аг = A12 + A23 + A31
• работу на процессе 1 - 2 найдем как площадь трапеции :
○ A12 = (P0 + 3P0) / 2 * (3V0 - V0) = 4 P0V0
• работу на процессе 2 - 3 ищем аналогично :
○ А23 = 2P0 * ( - V0) = - 2 P0V0
• работу на процессе 3 - 1 ищем через площадь прямоугольника :
• соответственно, работа газа за цикл равна Аг = P0V0
• чтобы найти количество теплоты от нагревателя, нам нужно, во - первых, понять, на каких участках газ получает тепло
• газ получает тепло на участках 1 - 2 и 2 - 3 (на нем хоть и отрицательная работа, приращение внутренней энергии больше).
• количество теплоты в обоих процессах ищем по 1 закону термодинамики
○ Q12 = A12 + ΔU12 = 4 P0V0 + 1.
5 * ΔPΔV = 6 P0V0
○ Q23 = A23 + ΔU23 = - 2P0V0 + 1.
• следовательно, Qн = 7P0V0
• и тогда КПД равен n = 1 / 7≈ 0.
КПД идеальной тепловой машины , работающей по циклу Карно , 25 %?
КПД идеальной тепловой машины , работающей по циклу Карно , 25 %.
На сколько процентов необходимо повысить температуру нагревателя этой машины , чтобы увеличить КПД в 2 раза ?
Температуру холодильника оставляют без изменения .
КПД идеальной тепловой машины работающей по циклу карно 40%?
КПД идеальной тепловой машины работающей по циклу карно 40%.
Какую полезную работу совершает за цикл эта машина , если она отдает холодильнику количество теплоты 300 Дж.
Помогите пожалуйста решить -Найти КПД тепловой машины, работающей по циклу, если рабочее тело - одноатомный идеальный газ?
Помогите пожалуйста решить -
Найти КПД тепловой машины, работающей по циклу, если рабочее тело - одноатомный идеальный газ.
Ответ выразите в процентах, до одной значащей цифры.
В тепловой машине, работающей по циклу Карно, температура нагревается в 4 раза выше температуры холодильника?
В тепловой машине, работающей по циклу Карно, температура нагревается в 4 раза выше температуры холодильника.
Нагреватель передает рабочему телу машины - идеальному газу кол - во теплоты 80 кДж.
Какую работу совершает машина за один цикл?
Температура тела, использующегося идеальный тепловой машиной Карно в качестве нагревателя, равна 727 градусам, а разность температур нагревателя и тела, использующегося этой машиной в качестве холодил?
Температура тела, использующегося идеальный тепловой машиной Карно в качестве нагревателя, равна 727 градусам, а разность температур нагревателя и тела, использующегося этой машиной в качестве холодильника, равна 600 К.
Какое количество теплоты за один цикл работы машины передается холодильнику, если нагреватель за один цикл передает рабочему телу количество теплоты, равное 1кДж?
Идеальная тепловая машина работает по циклу Карно?
Идеальная тепловая машина работает по циклу Карно.
При этом 80% тепла, полученного от нагревателя, передается холодильнику.
Найдите КПД цикла.
КПД идеальной тепловой машины работающей по циклу карно 40%?
КПД идеальной тепловой машины работающей по циклу карно 40%.
Какую полезную работу совершает за цикл эта машина , если она отдает холодильнику количество теплоты 300 Дж, реши ка).
Цикл тепловой машины состоит из двух изобар и двух адиабат?
Цикл тепловой машины состоит из двух изобар и двух адиабат.
Рабочее вещество – идеальный одноатомный газ.
Работа, совершённая над газом при изобарическом сжатии на 35% меньше работы газа при изобарическом расширении.
Найдите КПД тепловой машины.
Рабочее тело идеальной тепловой машины получает от нагревателя 70кДж энергии за цикл?
Рабочее тело идеальной тепловой машины получает от нагревателя 70кДж энергии за цикл.
Температура нагревателя в три раза выше температуры холодильника.
Найти работу, совершаемую рабочим телом за цикл.
Тепловая машина работает по циклу, состоящему из изобарного расширения, изохорного охлаждения и адиабатного сжатия?
Тепловая машина работает по циклу, состоящему из изобарного расширения, изохорного охлаждения и адиабатного сжатия.
Её рабочим телом является идеальный одноатомный газ.
КПД тепловой машины составляет η = 30%.
Какое количество теплоты отводится от газа в изохорном процессе, если в адиабатном процессе над газом совершается работа A = 2 кДж?
Вы находитесь на странице вопроса Рассчитайте КПД тепловой машины, использующей в качестве рабочего тела одноатомный идеальный газ и работающей по циклу, изображенному на рисунке? из категории Физика. Уровень сложности вопроса рассчитан на учащихся 10 - 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
Газ в нагретом состоянии производит большее давление, чем в холодном. Т. к. Нагретом состоянии скорость молекул больше и молекулы сильнее ударяются о стенку сосуда.
Потому что при сжатии расстояние между молекулами уменьшается, увеличивается число ударов молекул о стенки сосуда. Удары о стенки сосуда молекул и передача молекулами стенкам импульса. Есть давление газ.
Поршень является рабочим телом теплового двигателя.
R = ρL / S = U / I ρ = US / IL = [3 × 10 ^ ( - 6)] / (2 × 5) = 3 × 10 ^ ( - 7) Ом × м.
P = mg, m = p / g = 600H / 10(або 9, 8) = 60 кг (або 61 кг).
Р = рgh, где р - плотность воды Р = 45×10 ^ 6Па h = P / ph h = 45×10 ^ 6Па / (1000кг / м ^ 3×9, 8Н / кг) = 4500м = 4, 5км.
P = pgh h = p / pg h = 45000000 / 1000 * 10 = 4500 м = 4, 5 км.
F = k * q ^ 2 / R ^ 2 q = корень из (F * R ^ 2 / k ) F = 4 * 10 ^ - 4 Н R = 5 * 10 ^ - 2 м K = 9 * 10 ^ 9.
Тепловая машина использующая идеальный одноатомный газ работает по замкнутому циклу. КПД тепловой машины составляет..

Найдем работу, совершаемую газом, и изменение его внутренней энергии на участках АВ(1-2), ВС(2-3), CD(3-4), DA(4-1): AAB=0, (1) ΔUAB=CV(TB−TA)=CVT1ΔUAB=CV(TB−TA)=CVT1, ABC=p(VC−VB)=R(TC−TB)=2RT1ABC=p(VC−VB)=R(TC−TB)=2RT1, (2) ΔUBC=CV(TC−TB)=2CVT1ΔUBC=CV(TC−TB)=2CVT1, ACD=0ACD=0, (3) ΔUCD=CV(TD−TC)=−2CVT1ΔUCD=CV(TD−TC)=−2CVT1, ADA=p(VA−VD)=R(TA−TD)=−RT1ADA=p(VA−VD)=R(TA−TD)=−RT1, (4) ΔUDA=CV(TA−TD)=−CVT1ΔUDA=CV(TA−TD)=−CVT1. В этих формулах CV=3r/2,Cp=5R/2CV=3r/2,Cp=5R/2. Полезная работа, производимая газом за один цикл, равна сумме работ (1) - (4), производимых на отдельных участках цикла: A=AAB+ABC+ACD+ADA=RT1A=AAB+ABC+ACD+ADA=RT1.(5) Количество теплоты, получаемое газом на отдельных участках цикла определяется из первого начала термодинамики Q=ΔU+AQ=ΔU+A: QAB=ΔUAB=CVT1>0QAB=ΔUAB=CVT1>0, (6) QBC=ΔUBC+ABC=2(CV+R)T1=2CpT1>0QBC=ΔUBC+ABC=2(CV+R)T1=2CpT1>0, <7) QCD=ΔUCD=−2CVT1<0QCD=ΔUCD=−2CVT1<0, (8) QDA=ΔUDA+ADA=−(CV+R)(TA−TD)=−CpT1<0QDA=ΔUDA+ADA=−(CV+R)(TA−TD)=−CpT1<0. (9) Видим, что количество теплоты положительно на участках АВ, ВС и отрицательно на других участках. Следовательно, на участке АВС газ получает тепло от нагревателя, причем соответствующее количество теплоты надо рассматривать как затраченную энергию QнQн в определении КПД. В нашем случае оно равно сумме величин (6) и (7): Qн=QAB+QBC=132RT1Qн=QAB+QBC=132RT1. (10) Используя определение КПД η=A/Qнη=A/Qн, согласно (5) и (10) окончательно получаем η=2/13.
Поделись вопросом в социальных сетях!
Если Вы не получили ответ на свой вопрос, то предлагаем воспользоваться поиском, чтобы найти похожие вопросы и ответы по предмету -> Физика. А если Вы знаете правильный ответ сами, то будем признательны если Вы ответите, воспользовавшись формой ниже.
Двигатели тепловые
Рабочее вещество тепловой машины совершает цикл Карно (рис. ) между изотермами T и T1 (T1 > T). Холодильником является резервуар, температура которого постоянна и равна T2 = 200 К (T2 < T). Теплообмен между рабочим веществом и холодильником осуществляется посредством теплопроводности. Количество теплоты, отдаваемое в единицу времени холодильнику, q = a·(T - T2), где a = 1 кВт/Κ. Теплообмен рабочего вещества с нагревателем происходит непосредственно при T1 = 800 К. Полагая, что продолжительность изотермических процессов одинакова, а адиабатических весьма мала, найдите температуру «холодной» изотермы T, при которой мощность N тепловой машины наибольшая. Определите наибольшую мощность тепловой машины.
№ 16721
В тепловой машине в качестве рабочего тела используется идеальный одноатомный газ. На рисунке представлены циклы I и II, совершаемые этим газом. Найдите коэффициенты полезного действия (КПД) η1 и η2 этих циклов, если их отношение равно α = η1/η2 = 1,6.
№ 16729
В тепловой машине n молей идеального одноатомного газа совершают замкнутый цикл, состоящий из процессов 1-2 и 2-3, в которых давление p газа линейно зависит от занимаемого им объема V, и изохорического процесса 3-1 (рис. ). Величины p0 и V0 считайте известными. Найдите: 1) температуру и давление газа в точке 3; 2) работу A, совершаемую газом за цикл; 3) коэффициент полезного действия η тепловой машины.
№ 16751
Говорят, что в архиве лорда Кельвина нашли обрывок рукописи, на котором был изображен замкнутый цикл для n = 1 моль гелия в координатах p, V (рис. ). Цикл состоял из изотермы 1-2, изохоры 2-3 и адиабаты 3-1. КПД данного цикла η = 0,125. Найдите объем газа в изохорическом процессе, если на рисунке ось давления вертикальна, а ось объема горизонтальна. Масштаб по оси объема: 1 дел = 0,5 л; по оси давления: 1 дел = 5 кПа.
№ 16927
Экспериментатор Глюк исследовал неизвестный газ и обнаружил, что он подчиняется уравнению Менделеева-Клапейрона лишь приближенно. Зависимость его давления p от температуры T, объема V и количества молей ν можно описать формулой p = ν·R·T/V + ν 2 ·(b·T – a)/V 2 , где a и b - малые параметры. Глюк предположил, что выражение для внутренней энергии U также немного отличается от формулы в случае идеального газа и имеет вид: U = 3/2·ν·R·T – c·ν 2 /V.<br>Размышляя над различными способами измерения коэффициента c, Глюк вспомнил, что КПД цикла Карно зависит только от температур нагревателя и холодильника. Используя это утверждение, он определил значение коэффициента c без проведения измерений. Найдите c, считая известными a и b.
№ 16886
Рабочее вещество, внутренняя энергия которого U связана с давлением p и объемом V соотношением U = k·p·V, совершает термодинамический цикл, состоящий из изобары, изохоры и адиабаты. Работа, совершенная рабочим веществом во время изобарного процесса, в m = 5 раз превышает работу внешних сил по сжатию вещества, совершенную при адиабатном процессе. Коэффициент полезного действия цикла η = 1/4. Определите коэффициент k.
№ 16826
Периодически действующая установка (тепловая машина) использует тепловую энергию, переносимую теплым течением океана. Оцените максимальную полезную мощность, которую можно от нее получить, если скорость течения воды в месте расположения установки u = 0,1 м/с, средняя температура воды в поверхностном слое океана, толщина которого h = 1 км, T1 = 300 К, температура воздуха вблизи поверхности воды T2 = 280 К, размер установки в поперечном течению направлении L = 1 км, удельная теплоемкость воды c = 4200 Дж/(кг·К), плотность воды ρ = 10 3 кг/м 3 .
№ 16894
Один из спаев термопары находится при комнатной температуре (t1 = 27 °С), а второй - в теплоизолированном сосуде со льдом, имеющим температуру t2 = 0 °С. Мощность, развиваемая термопарой, выделяется на сопротивлении нагревателя, который помещен в другой теплоизолированный сосуд, содержащий воду (рис.). Оцените повышение температуры воды к моменту окончания плавления льда. Можно считать, что все электрическое сопротивление цепи сосредоточено в нагревателе. Массы воды и льда одинаковы. Удельная теплоемкость воды c = 4,2 кДж/(кг·К); удельная теплота плавления льда λ = 335 кДж/кг.
№ 16856
Идеальный холодильник, потребляющий во время работы из электросети мощность N = 100 Вт, находится в комнате, которую можно рассматривать как замкнутую теплоизолированную камеру объемом V = 100 м 3 . Начальные параметры воздуха в комнате: T0 = 300 К, давление p0 = 1 атм. В холодильную камеру устанавливается ванночка с водой при температуре Tх = 273 К. Масса воды m0 = 4 кг.<br>1. Какое минимальное время должен проработать холодильник, чтобы вода в ванночке замерзла?<br>2. Чему равна температура воздуха в комнате в этот момент?<br>Удельная теплота плавления льда q = 3,34·10 5 Дж/кг. Теплоемкость стен комнаты и стенок холодильника не учитывать. Считать относительное изменение температуры в комнате в результате работы холодильника малым. Воздух считать идеальным двухатомным газом.
№ 16883
С помощью бензиновой горелки в помещении поддерживается температура t1 = -3 °С при температуре на улице t2 = -23 °С. Предполагается использовать бензин в движке с КПД η = 0,4, ас помощью полученной механической энергии запустить тепловой насос, перекачивающий по идеальному холодильному циклу теплоту с улицы в комнату. Какую температуру t3 удастся в таком случае поддерживать в помещении при прежнем расходе бензина? Движок находится вне помещения.
Газовые законы. Термодинамика
Метод решения задач с использованием диаграмм состояния успешно зарекомендовал себя при изуче- нии тем «Газовые законы», «Термодинамика», «Тепловые двигатели». Этот метод может быть использован также и на уроках, и на факультативных занятиях.
1. При нагревании газа получена зависимость, показанная на рисунке. Определите, сжимался газ или расширялся? [Масса газа постоянна. – Ред. ]
Нужно провести из начала координат прямые (пунктир на чертеже),
проходящие через состояния 1 и 2.
Эти прямые соответствуют процессам при постоянных объемах V 1 и V 2 .
Поскольку V 2 > V 1 , газ расширялся.
2. Как менялась температура [заданной массы. – Ред .] идеального газа (увеличивалась или уменьшалась) в процессе, график которого в координатах p, V изображен на рисунке?
Проведем гиперболы, касательные к кривой. Так как гипербола в координатах p, V является графиком изотермы: pV = n RT = const, то T 1 < T 2 . Следовательно, от состояния 1 до состояния 2 температура газа повышалась, а от состояния 2 до состояния 1 – понижалась.
3. Получены две экспериментальные зависимости (см. рисунок). В каком случае масса газа больше? Давление в первом и во втором случае одинаково.
Так как V 1 > V 2 , то m 1 > m 2 .
4. Над идеальным газом производят два замкнутых процесса: 1–2–3–1 и 3–2–4–3 . В каком из них газ совершает бо1льшую работу?
Изобразим изменение состояния газа на p–V-диаграмме.
Очевидно, что А 2 > А 1 .
5. Моль идеального одноатомного газа переводится из начального состояния 1 в конечное состояние 4 в ходе процесса 1 – 2 – 3 – 4 . определите подведенное к газу количество теплоты, если разность начальной и конечной температур D T = 100 К. Считать R = 8,3 Дж/(моль • К).
Из р–Т- диаграммы видно, что T 2 – T 1 = T 4 – T 3 = D Т .
Воспользуемся формулой Q = D U + A ':
6. Моль одноатомного [идеального. – Ред .] газа совершает замкнутый цикл, состоящий из трех процессов: адиабатического расширения, изотермического сжатия и изохорного нагревания. Какая работа была совершена газом в адиабатическом процессе, если при изохорном нагревании подвели Q = 10 кДж тепла? R = 8,3 Дж/(К • моль). [Для произвольного идеального газа результат тот же. – Ред .]
T 2 = T 3 Ю – D U 31 = D U 12 .
V 1 = V 3 Ю Q 31 = D U 31 = 10 кДж, т.к. A' 31 = 0.
Таким образом, A ' 12 = – D U 12 = D U 31 = Q 31 = 10 кДж.
7. Один моль одноатомного идеального газа совершает замкнутый цикл, состоящий из процесса с линейной зависимостью давления от объема, изобары и изохоры. Найдите количество теплоты, подведенное к газу на участках цикла, где его температура растет. Температура газа в состояниях 1 и 2 равна 300 К. Отношение объемов на изобаре
Направление обхода цикла указано стрелками. R = 8,3 Дж/(моль • К).
б ) На участке 1–2 p = a – b V , т.е.:
p 1 = a – b V 1 ;
p 2 = a – b V 2 .
Решая систему, находим:
Умножив обе части на V , получим:
На участке 1–4 температура растет!
Q подвед = Q 31 + Q 14 = 1245 Дж + 726,25 Дж d 1970 Дж.
8. Состояние [одного моля идеального одноатомного. – Ред. ] газа меняется, как представлено на диаграмме p, T , причем p
T на участке 1–2 и на участке 2–3 . Найдите теплоемкости газа на участках 1–2 и 2–3 .
а ) На участке 1–2
б ) На участке 2–3 таким образом, V
p . Работа газа в этом случае:
[В решении этой задачи помещен рисунок, предложенный редакцией, т.к. авторский рисунок ошибочен. – Ред ]
9. КПД тепловой машины, работающей по циклу, состоящему из изотермы 1–2 , изохоры 2–3 и адиабаты 3–1 , равен h . Разность максимальной и минимальной температур газа в цикле равна D T .
Найдите работу, совершенную n молями одноатомного идеального газа в изотермическом процессе.
Q 12 – количество теплоты, полученное от нагревателя; Q 23 – количество теплоты, отданное холодильнику; Q 31 = 0, т.к. 3–1 – адиабата.
Задачи для самостоятельного решения
1. Поршень в цилиндре с воздухом прилегает к стенкам цилиндра неплотно, поэтому медленно пропускает воздух. Снятая во время нагревания при постоянном давлении зависимость объема от температуры изображена на рисунке. Увеличивалась или уменьшалась масса воздуха в цилиндре? ( Ответ . Масса газа в состоянии 1 больше, чем в состоянии 2. )
2. На рисунке показан циклический процесс, проведенный над некоторой массой [идеального. – Ред .] газа. Изобразите этот процесс в координатах p, T и V , T ( 1–2 и 4–5 – изотермы).
3. На p–T- диаграмме изображен замкнутый процесс, который совершает некоторая масса кислорода. Известно, что максимальный объем, который занимал газ в этом процессе, V макс = 16,6 дм 3 . Определите массу газа и его объем в точке 1 . Значения T 1 , T 2 , p 1 и p 2 указаны на рисунке.
( Ответ . V 1 = 12,4 дм 3 ; m = 16 г.)
4. Найдите работу, совершаемую молем идеального газа в цикле, состоящем из двух участков линейной зависимости давления от объема и изохоры. Точки 1 и 3 лежат на прямой, проходящей через начало координат. Температуры в точках 2 и 3 одинаковы. Считать заданными температуры T 1 и T 2 в точках 1 и 2 . ( Ответ )
5. В тепловом процессе моль [одноатомного. – Ред .] идеального газа переводят из начального состояния в конечное, как показано на рисунке. Какое количество теплоты подведено к газу, если разность начальной и конечной температур D T = 100 °C? ( Ответ . 415 Дж.)
6. Моль идеального газа переводят из состояния 1 в состояние 2 : в первом случае – адиабатически, а во втором – сначала по изобаре 1–3 , а затем по изохоре 3–2 .
Минимальная температура T мин = 300 К. Количество теплоты, подведенное к газу в процессе 1 – 3 – 2 , равно 2,6 кДж. Чему равна работа газа в адиабатическом процессе?
( Ответ . А 12 = – 12 560 Дж.)
7. Один моль идеального газа изменяет свое состояние согласно представленному циклу. 1–4 и 2–3 – изохоры, 3–4 – изобара, 1 – 2 – прямая. Температуры в состояниях 1 , 2 , 3 , 4 равны соответственно T 1 , T 2 , T 3 , T 4 . Какую работу совершает газ за один цикл?
8. В каждом из процессов, изображенных на диаграмме, температура изменяется на одну и ту же величину. В каком из этих процессов газ получает наибольшее количество теплоты? ( Ответ . в изобарном процессе.)
9. Состояние [моля идеального. – Ред .] газа меняется, как представлено на диаграмме p, V , причем p
V 2 на участке 1–2 . Найдите теплоемкость газа в этом процессе. ( Ответ . . )
[Авторский ответ ошибочен. – Ред .]
4 10. Найдите КПД тепловых машин, работающих по циклам 1–2–3–1 и 1–3–4–1 , если КПД машины, работающей по циклу 1–2–3–4–1 , равен h . В качестве рабочего тела во всех слу-
чаях используется [один и тот же. – Ред .] идеальный газ.
44 11. Определите КПД цикла, состоящего из двух адиабат и двух изохор, совершаемого одноатомным идеальным газом. Известно, что в процессе адиабатного расширения устанавливается температура T 2 = 0,75 T 1 , а в
Термодинамика
Два баллона, объёмами 60 л и 40 л, наполнены Неоном 80 г и Гелием 32 г соответственно. После соединения баллонов давление внутри 300 кПа. Определите температуру газов в конце процесса.
“Досрочная волна 2019 вариант 1”
Постоянную массу идеального одноатомного газа изобарно сжали так, что \(T_2=\dfrac
“Основная волна 2019”
При изобарном сжатии над гахов совершается работа, модуль которой \(A_1=|p\Delta V|\) где \(p\) – давление гелия в этом процессе, \(\Delta V\) – изменение его объёма.
В соответствии с уравнением Менделеева–Клапейрона для этого процесса можно записать: \[p\Delta V =\nu R (T_1-T_2)=A_1\] В адиабатном процессе (процессе без теплообмена) в соответствии с первым законом термодинамики сумма изменения внутренней энергии газа и его работы равна нулю: \[\dfrac<3><2>\nu R (T_3-T_2)+A_2=0\] При записи последнего соотношения учтено выражение для изменения внутренней энергии идеального одноатомного газа: \[\Delta U =\dfrac<3><2>\nu R (T_3-T_2)\] Преобразуя записанные уравнения с учётом соотношений температур, заданных в условии задачи, получаем: \[A_1=\nu RT_2(k-1)\hspace<5 mm>A_2=\dfrac<3><4>\nu RT_2\] По условию \(\dfrac
“Основная волна 2020 Вариант 2”
Количество теплоты, полученное системой равно \[Q=L\Delta m,\quad (1)\] где \(\Delta m\) – масса образовавшегося пара.
Так как процесс испарения прошел не до конца, то данный процесс изотермический, а значит изменение внутренней энергии будет за счет изменения массы пара \[A=\dfrac<\Delta m>
Объединим (1), (2) и (3) и найдем отношение \(\dfrac\) \[\dfrac
=\dfrac<\dfrac<\Delta m>
Сосуд объемом \(V=10\) л содержит \(\nu=5\) моль гелий при температуре \(t=17^\circ C\) . Если сообщить гелию количество теплоты \(Q=3\) кДж, то сосуд лопнет. Какую максимальную разность давлений внутри сосуда и снаружи него он выдерживает? Атмосферное давление \(p_0=10^5\) Па.
“Основная волна 2020 Вариант 3”
Гелий в количестве \(\nu\) = 3 моль изобарно сжимают, совершая работу \(A_1\) = 2,4 кДж. При этом температура гелия уменьшается в 4 раза: \(T_2=\dfrac
При изобарном сжатии над гелием совершается работа, модуль которой \(A_1=|p\Delta V|\) где \(p\) – давление гелия в этом процессе, \(\Delta V\) – изменение его объёма.
В соответствии с уравнением Менделеева–Клапейрона для этого процесса можно записать: \[p\Delta V =\nu R (T_1-T_2)\] В адиабатном процессе (процессе без теплообмена) в соответствии с первым законом термодинамики сумма изменения внутренней энергии газа и его работы равна нулю: \[\dfrac<3><2>\nu R (T_3-T_2)+A_2=0\] При записи последнего соотношения учтено выражение для изменения внутренней энергии идеального одноатомного газа: \[\Delta U =\dfrac<3><2>\nu R (T_3-T_2)\] Преобразуя записанные уравнения с учётом соотношений температур, заданных в условии задачи, получаем: \[A_1=3\nu RT_2\hspace<5 mm>A_2=\dfrac<3><4>\nu RT_2\] Получаем: \[A_2=\dfrac
Количество теплоты, полученное системой равно \[Q=L\Delta m,\quad (1)\] где \(\Delta m\) – масса образовавшегося пара.
Так как процесс испарения прошел не до конца, то данный процесс изотермический, а значит изменение внутренней энергии будет за счет изменения массы пара \[A=\dfrac<\Delta m>
Объединим (1), (2) и (3) и найдем отношение \(\dfrac\) \[\dfrac
=\dfrac<\dfrac<\Delta m>
С одним молем идеального одноатомного газа проводят циклический процесс 1-2-3-1, где 1-2 – адиабата, 2-3 – изобара, 3-1 – изохора. Температуры в точках 1, 2, 3 равны 600 К, 455 К и 300 К соответственно. Найдите КПД цикла.

“Досрочная волна 2019 вариант 2”
Цикл не является циклом идеальной тепловой машины. Поэтому воспользуемся общей формулой через теплоту нагревателя и теплоту холодильника. \[\eta = \dfrac
\[Q_<23>=A_<23>+\Delta U_<23>=p_<2>\left(V_<3>-V_<2>\right)+\frac<3> <2>v R\left(T_<3>-T_<2>\right)=\] \[=\left(p_ <2>V_<3>-p_ <2>V_<2>\right)+\frac<3> <2>v R\left(T_<3>-T_<2>\right)=\left(v R T_<3>-v R T_<2>\right)+\frac<3> <2>v R\left(T_<3>-T_<2>\right)=\] \[=\frac<5> <2>v R\left(T_<3>-T_<2>\right)<0\] \[Q_\text<х>=\left|Q_<23>\right|=\frac<5> <2>v R\left(T_<2>-T_<3>\right)\] 3.На участке 3–1 объём газ постоянен, работа равна нулю: \[Q_<31>=A_<31>+\Delta U_<31>=\Delta U_<31>=\frac<3> <2>v R\left(T_<1>-T_<3>\right)>0\] Теплота получилась на этом участке положительной, а значит, газ получает теплоту от нагревателя \[Q_\text<н>=Q_<31>=\frac<3> <2>v R\left(T_<1>-T_<3>\right)\] 4. Найдём значение КПД: \[\eta=1-\frac
Тепловые двигатели. Термодинамические циклы. Цикл Карно
Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.
Как следует из первого закона термодинамики, полученное газом количество теплоты Q полностью превращается в работу A при изотермическом процессе, при котором внутренняя энергия остается неизменной (ΔU = 0):
Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме (p, V) газообразного рабочего тела с помощью замкнутых кривых (рис. 3.11.1). При расширении газ совершает положительную работу A1, равную площади под кривой abc, при сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A = A1 + A2 на диаграмме (p, V) равна площади цикла. Работа A положительна, если цикл обходится по часовой стрелке, и A отрицательна, если цикл обходится в противоположном направлении.
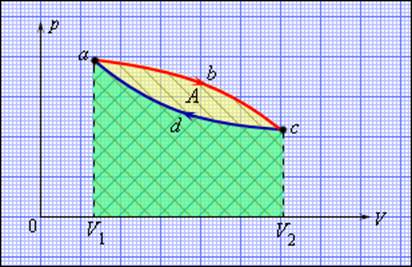
Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd
Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 < 0. Полное количество теплоты Q, полученное рабочим телом за цикл, равно
При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (ΔU = 0). Согласно первому закону термодинамики,
Работа A, совершаемая рабочим телом за цикл, равна полученному за цикл количеству теплоты Q. Отношение работы A к количеству теплоты Q1, полученному рабочим телом за цикл от нагревателя, называется коэффициентом полезного действия η тепловой машины:
Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1). Энергетическая схема тепловой машины изображена на рис. 3.11.2.
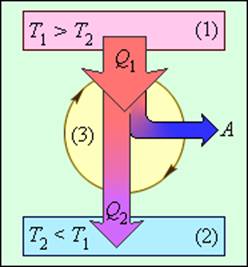
Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1 > 0, A > 0, Q2 < 0; T1 > T2
В двигателях, применяемых в технике, используются различные круговые процессы. На рис. 3.11.3 изображены циклы, используемые в бензиновом карбюраторном и в дизельном двигателях. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.
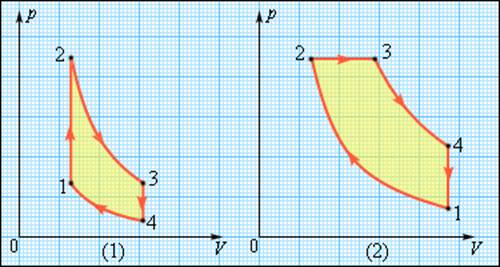
Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2)
В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 < T1. Происходит процесс изотермического сжатия. Газ совершает работу A34 < 0 и отдает тепло Q2 < 0, равное произведенной работе A34. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T1, газ совершает работу A41 < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:
На диаграмме (p, V) эта работа равна площади цикла.
Процессы на всех участках цикла Карно предполагаются квазистатическими. В частности, оба изотермических участка (1–2 и 3–4) проводятся при бесконечно малой разности температур между рабочим телом (газом) и тепловым резервуаром (нагревателем или холодильником).
Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для 1 моля газа
где T1 и T2 – начальная и конечная температуры газа.
Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам
По определению, коэффициент полезного действия η цикла Карно есть

С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя T1 и холодильника T2:
Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, т. е. бесконечно близким к состоянию теплового равновесия с окружающими телами (тепловыми резервуарами или термостатами). Цикл Карно исключает теплообмен при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника:
Любой участок цикла Карно и весь цикл в целом может быть пройден в обоих направлениях. Обход цикла по часовой стрелке соответствует тепловому двигателю, когда полученное рабочим телом тепло частично превращается в полезную работу. Обход против часовой стрелки соответствует холодильной машине, когда некоторое количество теплоты отбирается от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Поэтому идеальное устройство, работающее по циклу Карно, называют обратимой тепловой машиной.
В реальных холодильных машинах используются различные циклические процессы. Все холодильные циклы на диаграмме (p, V) обходятся против часовой стрелки. Энергетическая схема холодильной машины представлена на рис. 3.11.5.
Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q2| от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением
т. е. эффективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении βх может быть и больше, и меньше единицы. Для обращенного цикла Карно
Если полезным эффектом является передача некоторого количества тепла |Q1| нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность βТ теплового насоса может быть определена как отношение
т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:
следовательно, βТ всегда больше единицы. Для обращенного цикла Карно
Читайте также:

