Тело плавает в жидкости или газе если
Архимедова сила: что это такое и как действует
Гениальный учёный Архимед, живший в древнегреческих Сиракузах в III веке до нашей эры, прославился среди современников как создатель оборонительных машин, способных перевернуть боевой корабль. Другое его изобретение, «Архимедов винт», по сей день остаётся важнейшей деталью гигантских буровых установок и кухонных мясорубок. Мир обязан Архимеду революционными открытиями в области оптики, математики и механики.
Его личность окутана легендами, порой весьма забавными. С одной из них мы и начнём нашу статью.
«Эврика!» Открытие закона Архимеда
Однажды царь Сиракуз Гиерон II обратился к Архимеду с просьбой установить, действительно ли его корона выполнена из чистого золота, как утверждал ювелир. Правитель подозревал, что мастер прикарманил часть драгоценного металла и частично заменил его серебром.
В те времена не существовало способов определить химический состав металлического сплава. Задача поставила учёного в тупик. Размышляя над ней, он отправился в баню и лёг в ванну, до краёв наполненную водой. Когда часть воды вылилась наружу, на Архимеда снизошло озарение. Такое, что учёный голышом выскочил на улицу и закричал «Эврика!», что по-древнегречески означает «Нашёл!».

Он предположил, что вес вытесненной воды был равен весу его тела, и оказался прав. Явившись к царю, он попросил принести золотой слиток, равный по весу короне, и опустить оба предмета в наполненные до краёв резервуары с водой. Корона вытеснила больше воды, чем слиток. При одной и той же массе объём короны оказался больше, чем объём слитка, а значит, она обладала меньшей плотностью, чем золото. Выходит, царь правильно подозревал своего ювелира.
Так был открыт принцип, который теперь мы называем законом Архимеда:
На тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа в объёме погружённой части тела.
Эта выталкивающая сила и называется силой Архимеда.
Формула силы Архимеда
На любой объект, погружённый в воду, действует выталкивающая сила, равная весу вытесненной им жидкости. Таким образом, вес объекта, погружённого в воду, будет отличаться от его веса в воздухе в меньшую сторону. Разница будет равна весу вытесненной воды.
Чем больше плотность среды — тем меньше вес. Именно поэтому погрузившись в воду, мы можем легко поднять другого человека.
Выталкивающая сила зависит от трёх факторов:
- плотности жидкости или газа (p);
- ускорения свободного падения (g);
- объёма погружённой части тела (V).

Сопоставив эти данные, получаем формулу:
Как действует сила Архимеда
Поскольку сила Архимеда, действующая на тело, зависит от объёма его погружённой части и плотности среды, в которой оно находится, можно рассчитать, как поведёт себя то или иное тело в определённой жидкости или газе.

Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности.
Если плотности тела и жидкости или газа равны — тело будет находиться в безразличном равновесии в толще жидкости или газа.
Если плотность тела больше, чем плотность жидкости или газа, — оно уйдёт на дно.
Сила Архимеда в жидкости: почему корабли не тонут
Корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Но если корабль получит пробоину и пространство внутри заполнится водой, то общая плотность судна увеличится, и оно утонет.
В подводных лодках существуют специальные резервуары, заполняемые водой или сжатым воздухом в зависимости от того, нужно ли уйти на глубину или подняться ближе к поверхности. Тот же самый принцип используют рыбы, наполняя воздухом специальный орган — плавательный пузырь.
На тело, плотно прилегающее ко дну, выталкивающая сила не действует. Это учитывают при подъёме затонувших кораблей. Сначала судно слегка приподнимают, позволяя воде проникнуть под него. Тогда давление воды начинает действовать на корабль снизу.
Но чтобы поднять корабль на поверхность, необходимо уменьшить его плотность. Разумеется, воздух в получившем пробоину корпусе не удержится. Поэтому его заполняют каким-нибудь лёгким веществом, например, шариками пенополистирола.
Примечательно, что эта идея впервые пришла в голову не учёным, а авторам диснеевского комикса, в котором Дональд Дак таким образом поднимает со дна яхту Скруджа Макдака. Датский инженер Карл Кройер (Karl Krøyer), впервые применивший метод на практике, по собственному признанию вдохновлялся «Утиными историями».

Сила Архимеда в газах: почему летают дирижабли
В воздухе архимедова сила действует так же, как в жидкости. Но поскольку плотность воздуха обычно намного меньше, чем плотность окружённых им предметов, выталкивающая сила оказывается ничтожно мала.
Впрочем, есть исключения. Воздушный шарик, наполненный гелием, стремится вверх именно потому, что плотность гелия ниже, чем плотность воздуха. А если наполнить шар обычным воздухом — он упадёт на землю. Плотность воздуха в нём будет такая же, как у воздуха снаружи, но более высокая плотность резины обеспечит падение шарика.
Этот принцип используется в аэростатах — воздушные шары и дирижабли наполняют гелием или горячим воздухом (чем горячее воздух, тем ниже его плотность), чтобы подняться, и снижают концентрацию гелия (или температуру воздуха), чтобы спуститься. На них действует та же выталкивающая сила, что и на подводные лодки. Именно поэтому перемещения на аэростатах называют воздухоплаванием.
Статика. Закон Архимеда.
Закон Архимеда — закон статики жидкостей и газов, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа) и направленная по вертикали вверх.
Этот закон был открыт древнегреческим ученым Архимедом в III в. до н. э. Свои исследования Архимед описал в трактате «О плавающих телах», который считается одним из последних его научных трудов.
Ниже приведены выводы, следующие из закона Архимеда.
Действие жидкости и газа на погруженное в них тело .
Если погрузить в воду мячик, наполненный воздухом, и отпустить его, то он всплывет. То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?
На тело, погруженное в воду, со всех сторон действуют силы давления воды (рис. а). В каждой точке тела эти силы направлены перпендикулярно его поверхности. Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростатическое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих иа тело сверху.
Если заменить все силы давления, приложенные к погруженному в воду телу, одной (результирующей или равнодействующей) силой, оказывающей на тело то же самое действие, что и все эти отдельные силы вместе, то результирующая сила будет направлена вверх. Это и заставляет тело всплывать. Эта сила называется выталкивающей силой, или архимедовой силой (по имени Архимеда, который впервые указал на ее существование и установил, от чего она зависит). На рисунке б она обозначена как FA.

Архимедова (выталкивающая) сила действует на тело не только в воде, но и в любой другой жидкости, т. к. в любой жидкости существует гидростатическое давление, разное на разных глубинах. Эта сила действует и в газах, благодаря чему летают воздушные шары и дирижабли.
Благодаря выталкивающей силе вес любого тела, находящегося в воде (или в любой другой жидкости), оказывается меньше, чем в воздухе, а в воздухе меньше, чем в безвоздушном пространстве. В этом легко убедиться, взвесив гирю с помощью учебного пружинного динамометра сначала в воздухе, а затем опустив ее в сосуд с водой.
Уменьшение веса происходит и при переносе тела из вакуума в воздух (или какой-либо другой газ).
Если вес тела в вакууме (например, в сосуде, из которого откачан воздух) равен P0, то его вес в воздухе равен:
,
где F´A — архимедова сила, действующая на данное тело в воздухе. Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что Pвозд.=P0=mg.
Вес тела в жидкости уменьшается значительно сильнее, чем в воздухе. Если вес тела в воздухе Pвозд.=P0, то вес тела в жидкости равен Pжидк = Р0 — FA. Здесь FA — архимедова сила, действующая в жидкости. Отсюда следует, что
Поэтому чтобы найти архимедову силу, действующую на тело в какой-либо жидкости, нужно это тело взвесить в воздухе и в жидкости. Разность полученных значений и будет архимедовой (выталкивающей) силой.
Другими словами, учитывая формулу (1.32), можно сказать:
Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.
Определить архимедову силу можно также теоретически. Для этого предположим, что тело, погруженное в жидкость, состоит из той же жидкости, в которую оно погружено. Мы имеем право это предположить, так как силы давления, действующие на тело, погруженное в жидкость, не зависят от вещества, из которого оно сделано. Тогда приложенная к такому телу архимедова сила FA будет уравновешена действующей вниз силой тяжести mжg (где mж — масса жидкости в объеме данного тела):
.
Но сила тяжести равна весу вытесненной жидкости Рж. Таким образом.
.
Учитывая, что масса жидкости равна произведению ее плотности ρж на объем, формулу (1.33) можно записать в виде:
где Vж — объем вытесненной жидкости. Этот объем равен объему той части тела, которая погружена в жидкость. Если тело погружено в жидкость целиком, то он совпадает с объемом V всего тела; если же тело погружено в жидкость частично, то объем Vж вытесненной жидкости меньше объема V тела (рис. 1.39).
Формула (1.33) справедлива и для архимедовой силы, действующей в газе. Только в этом случае в нее следует подставлять плотность газа и объем вытесненного газа, а не жидкости.

С учетом вышеизложенного закон Архимеда можно сформулировать так:
На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или газа), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).
Условия плавания тел

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина любого действия или взаимодействия — ее величество сила.
- Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.

Закон Архимеда
Этот закон известен преимущественно не своей формулировкой, а историей его возникновения.
Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом, не причиняя вреда самой короне. То есть, нельзя ее расплавить или в чем-нибудь растворить.
Взвесить корону Архимеду труда не составило, но этого было мало — нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.
Это можно сделать по формуле плотности.
Формула плотности тела
ρ — плотность тела [кг/м^3]
m — масса тела [кг]
V — объем тела [м^3]
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (по легенде он даже не оделся).
Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.
На поверхность твердого тела, погруженного в жидкость или газ, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.
Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.
Сила Архимеда
ρ ж — плотность жидкости [кг/м^3]
V погр — объем погруженной части тела [м^3]
g — ускорение свободного падения [м/с^2]
На планете Земля: g = 9,8 м/с^2
А теперь давайте порешаем задачки.
Задача 1
В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? (Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой).

Решение:
Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.
Задача 2
На поверхности воды плавают бруски из дерева, пробки и льда. Укажите, какой брусок из пробки, а какой изо льда? Какая существует зависимость между плотностью тела и объемом этого тела над водой?

Решение:
Чем меньше плотность тела, тем большая часть его находится над водой. Дерево плотнее пробки, а лед плотнее дерева. Значит изо льда — материал №1, а из пробки — №3.
Задача 3
На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ускорение свободного падения принять равным 10 м/с2.

Решение:
Сила Архимеда, действующая на кубик равна FАрх = ρж * g * Vпогр
V — объём погруженной части кубика,
ρ — плотность жидкости.
Учитывая, что нижнее основание кубика всё время параллельно поверхности жидкости, можем записать:
а — длина стороны кубика.
ρ = FАрх / (g * a 2 * x)
Рассматривая любую точку данного графика, получим:
ρ = FАрх / (g * a 2 * x) = 20,25 / (10 * 7,5 * 10 -2 ) = 2700 кг/м3
Ответ: плотность жидкости равна 2700 кг/м3
Задача 4
В сосуде с водой, не касаясь стенок и дна, плавает деревянный кубик с длиной ребра 20 см. Кубик вынимают из воды, заменяют половину его объёма на материал, плотность которого в 6 раз больше плотности древесины, и помещают получившийся составной кубик обратно в сосуд с водой. На сколько увеличится модуль силы Архимеда, действующей на кубик? (Плотность сосны — 400 кг/м3.)
Решение:
В первом случае кубик плавает в воде, а это значит, что сила тяжести уравновешивается силой Архимеда:
FАрх1 = mg = ρт * g * a 3 = 400 * 0,2 3 * 10 = 32 Н
После замены части кубика его средняя плотность станет равной
0,5 * 400 + 0,5 * 2400 = 1400 кг/м3
Получившаяся плотность больше плотности воды = 100 кг/м3. Это значит, что во втором случае кубик полностью погрузится в воду. Сила Архимеда в этом случае будет равна:
FАрх2 = ρт * g * Vт = 1000 * 10 * 0,23 = 80 Н
Отсюда получаем, что сила Архимеда увеличится на 48 Н.
Ответ: сила Архимеда увеличится 48 Н
Плавание тел
Из закона Архимеда есть следствия об условиях плавания тел.
Условия плавания тел
Плавание внутри жидкости
Плавание на поверхности жидкости



Если плотность тела больше, чем плотность жидкости или газа, — оно уйдёт на дно
Если плотности тела и жидкости или газа равны — тело будет находиться в безразличном равновесии в толще жидкости или газа.
Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности.
Почему корабли не тонут?
Корабль сделан из металла, плотность которого больше плотности воды. И, по идее, он должен тонуть. Но дело в том, что корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Если корабль получит пробоину, то пространство внутри заполнится водой — следовательно, общая плотность корабля увеличится. Судно утонет.
В подводных лодках есть специальные резервуары, заполняемые водой или сжатым воздухом. Если нужно уйти на глубину — водой, если подняться — сжатым воздухом. Рыбы используют такой же принцип в плавательном пузыре — наполняют его воздухом, чтобы подняться наверх.
Человеку, чтобы не утонуть, тоже достаточно набрать в легкие воздух и не двигаться — вода будет выталкивать тело на поверхность. Именно поэтому важно не тратить силы и кислород в легких на панику и борьбу, а расслабиться и позволить физическим законам сделать все за нас.
Тело плавает в жидкости или газе если
![]()
![]()
![]()
![]()

Закон Архимеда. Условие плавания тел
Код ОГЭ 1.22. Закон Архимеда. Формула для определения выталкивающей силы, действующей на тело, погружённое в жидкость или газ. Условие плавания тел. Плавание судов и воздухоплавание
Выталкивающая сила, действующая на тело со стороны жидкости и газа (общий случай).

Увеличение гидростатического давления по мере погружения в жидкость или газ является причиной возникновения выталкивающей силы: Fвыт = F1 – F2.
Сила Архимеда – выталкивающая сила, действующая на тело со стороны жидкости (газа) в случаях, если:
- тело полностью погружено в жидкость (газ), при этом со всех сторон окружено жидкостью (газом);
- тело плавает на поверхности жидкости, частично погрузившись в неё.
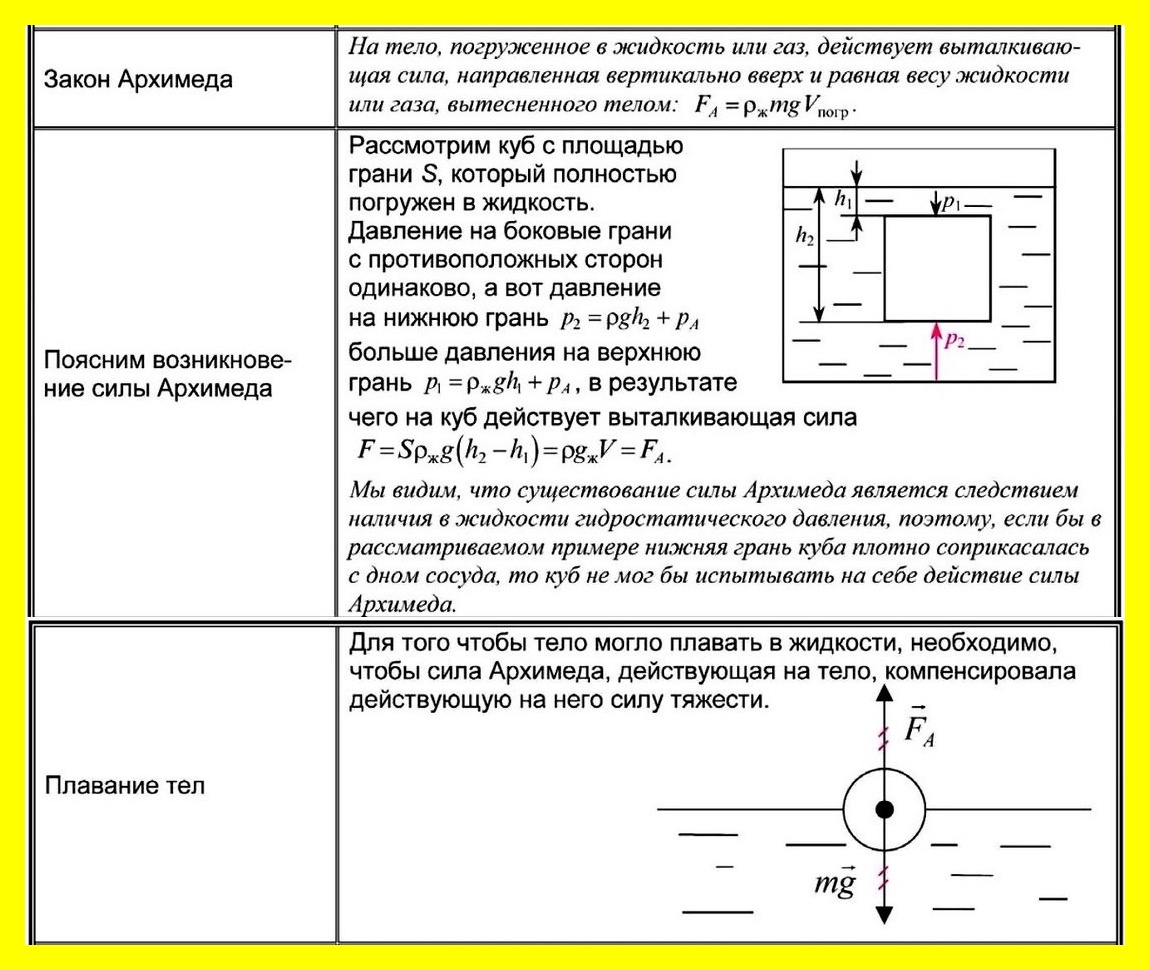
Закон Архимеда: На тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (газа), вытесненной телом. .
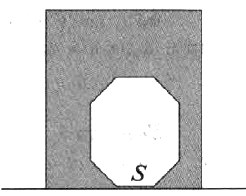
Внимание! Выталкивающую силу не всегда удаётся рассчитать с помощью формулы FА = ржgVпчт. Например, часть поверхности тела площадью S плотно соприкасается с дном сосуда. В этом случае выталкивающая сила будет равна F = pжgVт – FдS, где Fд – сила гидростатического давления жидкости на уровне дна сосуда.
- Если тело плотно прилегает ко дну, значит, под телом жидкости нет и нет силы давления, направленной вверх. Архимедова сила не действует, тело прижимается верхним слоем жидкости ко дну.
- Если какая-то часть поверхности тела плотно прилегает ко дну, а под другой частью поверхности есть жидкость, то нужно провести расчёт выталкивающей силы для данного конкретного случая. Для этого нужно подсчитать силы давления, действующие на верхнюю поверхность тела, и те части нижней поверхности тела, под которыми находится слой жидкости.
Условия плавания тел
- Тело целиком погружено в жидкость. Выталкивающая сила больше силы тяжести: Fвыт > mg (ржидкости > ртела). Тело всплывает до тех пор, пока силы не уравновесятся за счёт уменьшения выталкивающей силы (уменьшается объём погружённой в жидкость части тела).
- Тело целиком погружено в жидкость. Выталкивающая сила равна силе тяжести: Fвыт = mg (ржидкости = ртела). Тело плавает в любой точке жидкости (газа).
- Тело целиком погружено в жидкость. Выталкивающая сила меньше силы тяжести: Fвыт < mg (ржидкости < ртела). Тело тонет.

Физика 7 класс. Архимедова сила. Конспект

Действие жидкости и газа на погруженное в них тело. Архимедова сила. Плавание тел.
На тело, находящееся в жидкости, действует сила, выталкивающая это тело из жидкости. На тела, находящиеся в газе, действует сила, выталкивающая их из газа.
Сила, выталкивающая тело из жидкости или газа, направлена противоположно силе тяжести, приложенной к этому телу.
Поэтому если взвесить какое-либо тело в жидкости или газе, то его вес окажется меньше веса в вакууме. Именно этим объясняется, что в воде человек легко поднимает тела, которые с трудом удерживает в воздухе.
Сила, выталкивающая целиком погружённое в жидкость тело, равна весу жидкости в объеме этого тела.
Сила, выталкивающая тело из газа, также равна весу газа, взятого в объеме тела.
Силу, выталкивающую тело из жидкости или газа, называют архимедовой силой FA
в честь древнегреческого учёного Архимеда, который впервые указал на её существование и рассчитал её значение.

то есть, архимедова сила зависит от плотности жидкости ρ, в которую погружено тело, и от объёма V этого тела.
Если тело погружено в жидкость (или газ), то оно теряет в своем весе столько, сколько весит вытесненная им жидкость (или газ).

На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх.
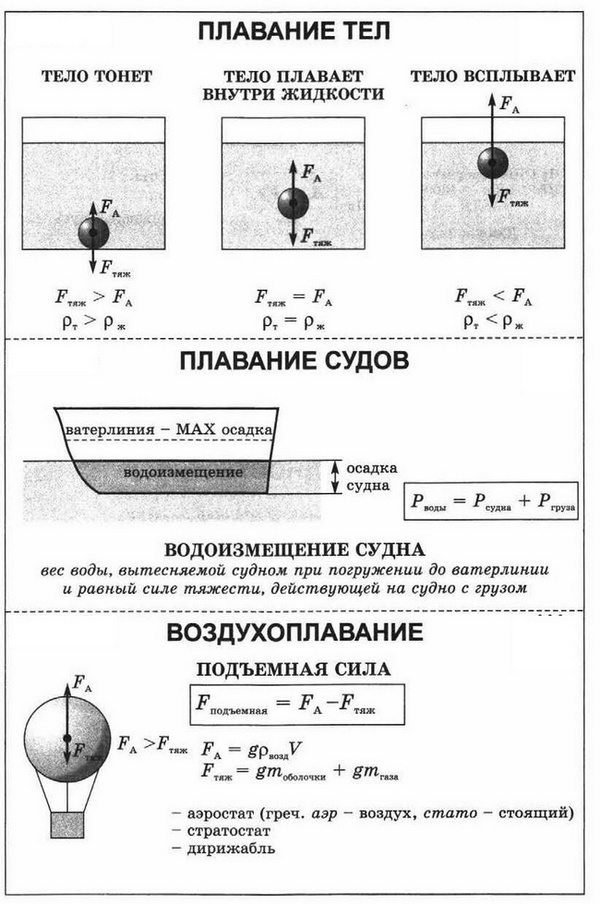
1. Если сила тяжести Fтяж больше архимедовой силы FA, то тело будет опускаться на дно, тонуть:
F тяж > FA, тело тонет
2. Если сила тяжести Fтяж равна архимедовой силе FA, то тело может находиться в равновесии в любом месте жидкости:
F тяж = FA, тело плавает
3. Если сила тяжести Fтяж меньше архимедовой силы FA, то тело будет подниматься из жидкости, всплывать:
F тяж < FA, тело всплывает
Если тело плавает в жидкости, то вес вытесненной им жидкости равен весу этого тела в воздухе.
Если плотность сплошного твердого тела больше плотности жидкости, то тело в такой жидкости тонет. Тело с меньшей плотностью всплывает в этой жидкости.
Пример:
кусок железа тонет в воде, но всплывает в ртути.
Тело, плотность которого равна плотности жидкости, остаётся в равновесии внутри жидкости.

Вес воды, вытесняемой подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Глубину, на которую судно погружается в воду, называют осадкой. Наибольшая допускаемая осадка отмечена на корпусе судна красной линией, называемой ватерлинией.
Вес воды, вытесняемой судном при погружении до ватерлинии, равный силе тяжести, действующей на судно с грузом, называется водоизмещением судна.
Если из водоизмещения вычесть вес самого судна, то получим грузоподъемность этого судна. Грузоподъемность показывает вес груза, перевозимого судном.
Плавание тел
Если тело находится в жидкости или газе, но на него действует выталкивающая сила, называемая силой Архимеда. Она возникает как результат того, что давление в жидкости (газе) увеличивается с погружением в глубину вещества. При этом сила гидростатического давления на тело в жидкости (газе) сверху вниз меньше, силы давления, направленной снизу вверх.
Сила Архимеда ($F_A)$ равна весу жидкости (газа) в объеме тела, находящегося в ней:
\[F_A=\rho Vg\ \left(1\right),\]
где $\rho $ - плотность жидкости (газа); $V$ - объем тела, находящийся в веществе; $g$ - ускорение свободного падения.
Сила Архимеда появляется только тогда, когда на жидкость (газ) действует сила тяжести. Так, в невесомости гидростатическое давление равно нулю соответственно, нет силы Архимеда.
И так, если тело погружено в жидкость, при этом оно находится в состоянии механического равновесия, то со стороны окружающей жидкости на тело действует выталкивающая сила (сила Архимеда). Данная сила направлена вверх. Она проходит через центр масс жидкости, вытесненной телом (обозначим эту точку буквой А). Точку А называют центром плавучести тела. Положением точки плавучести определяют равновесие и устойчивость плавающего тела.
Условия плавания тел
Закон Архимеда дает разъяснение всех вопросов, связанных с плаванием тел. Допустим, что тело находится в жидкости и оно предоставлено самому себе. Если вес тела больше, чем вес жидкости, которую оно вытесняет, то тело тонет. Если вес тела равен весу вытесненной им жидкости, то тело находится в равновесии внутри этой жидкости в любой ее точке. Если вес тела меньше, чем вес вытесненной им жидкости, то тело всплывает, двигаясь к поверхности жидкости. Достигнув поверхности, тело плавает так, что его часть выступает над поверхностью жидкости. Плавающие тела, обладающие разными плотностями, имеют над поверхностью жидкости разные доли своего объема.
Если тело, находящееся в жидкости, однородно ( то есть его плотность ($\rho =const$) постоянна), то условия плавания тел в жидкости ($<\rho >_g-$плотность жидкости) формулируют так$:$
- При $\rho ><\rho >_g$, тело тонет;
- При $\rho Пример 1
Задание: Тело плавает на поверхности вещества, плотность которого равна $<\rho >_1$, при этом объем погруженной части тела составляет $n\ $- ую часть от всего объема тела. Какая часть объема тела при его плавании будет погружена в жидкость, плотность которой составит $<\rho >_2?$ Тело считать однородным.
Решение: Для того чтобы тело плавало в жидкости вес этого тела должен быть равен весу жидкости объем которой равен объему тела, находящейся в ней, поэтому для первой жидкости запишем, что:
где $m=\rho Vg$- масса плавающего тела; $\rho $ - плотность тела.\textit<>
Выразим плотность тела, используя выражение (1.1):
Условием плавания тела того же тела во второй жидкости станет:
где $V_x$ - объем тела погруженный во вторую жидкость. Найдем отношение $\frac
Ответ: Погруженная часть составит $\frac
Задание: Тело полностью погружено в жидкость и плавает в ней. Объясните, почему равновесие будет устойчивым, если центр масс тела находится ниже центра его плавучести.
Решение: При нормальном положении центр тяжести и центр плавучести находятся на одной вертикальной прямой (рис.1 (а)). Центр плавучести (А) выше центра тяжести (B). Тело находится в равновесии. Тело наклоняется (рис.1(б)), при этом сила тяжести и сила Архимеда образуют пару сил, которая возвращает тело в исходное положение. Если центр плавучести будет находиться ниже центра тяжести, при отклонении от вертикального положения сила тяжести и сила выталкивания образуют пару сил, которая поворачивает тело дальше от положения равновесия (рис.1(в)).
Если центр тяжести совпадает с центром плавучести, то равновесие называют безразличным. В этом случае центр плавучести играет роль точки повеса.
Физика
На тело, погруженное в жидкость (или газ), действует выталкивающая сила — сила Архимеда .
- численно равна весу жидкости, вытесненной телом:
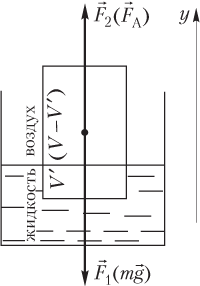
где ρ 0 — плотность жидкости (или газа); g — модуль ускорения свободного падения; V ′ — объем погруженной в жидкость (или газ) части тела;
- направлена вертикально вверх;
- приложена к центру тяжести жидкости (или газа), которая заполняла бы объем, занятый погруженным в нее телом (т.е. к центру тяжести вытесненной жидкости).
Сила Архимеда представляет собой равнодействующую сил давления, действующих со стороны жидкости (или газа) на помещенное в нее (в него) тело.
Подъемная сила — это равнодействующая силы тяжести m g → и силы Архимеда F → А :
F → под = F → А + m g → ,
где F → А — сила Архимеда; m g → — сила тяжести; m — масса тела; g → — ускорение свободного падения.
Величина подъемной силы определяется разностью:
Если величина подъемной силы
- положительная, то тело плавает на поверхности жидкости, частично погружаясь в нее;
- отрицательная — тело тонет ;
- равна нулю — тело находится в состоянии безразличного равновесия (плавает на любой глубине).
Условием плавания тела в жидкости (или газе) является равенство модулей силы Архимеда и силы тяжести:
где F A = ρ 0 gV ′ — модуль силы Архимеда; ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; V ′ — объем погруженной в жидкость части тела; mg — модуль силы тяжести; m = ρ т V т — масса тела; ρ т — плотность тела; V т — объем тела.
Сила Архимеда определяется произведением:
где ρ 0 — плотность жидкости (или газа); V ′ — объем погруженной в жидкость (или газ) части тела;
Сила тяжести определяется также произведением:
где ρ т — плотность тела; V т — объем тела.
Тело может плавать не только на поверхности жидкости, но и на любой глубине (то есть погрузившись полностью).
- ρ т < ρ 0 (плотность тела меньше плотности жидкости), то тело плавает на поверхности жидкости;
- ρ т > ρ 0 (плотность тела больше плотности жидкости), то тело тонет ;
- ρ т = ρ 0 (плотность тела равна плотности жидкости), то тело плавает на любой глубине — состояние безразличного равновесия .
Пример 32. Некоторое тело обладает плотностью 1,2 г/см 3 . Если поместить его в жидкость, имеющую плотность 3,0 г/см 3 , то оно будет плавать на ее поверхности. Определить, какая часть плавающего тела при этом находится в воздухе.
Решение . На тело, плавающее в жидкости, действуют две силы, показанные на рисунке:
- сила тяжести, модуль которой определяется формулой
где m = ρ V — масса тела; ρ — плотность тела; V — объем тела; g — модуль ускорения свободного падения;
- сила Архимеда, модуль которой определяется формулой
F 2 = F A = ρ 0 V ′ g ,
где ρ 0 — плотность жидкости; V ′ — объем погруженной в жидкость части тела.
Под действием указанных сил тело находится в равновесии (плавает); условие равновесия определяется равенством
или в проекции на вертикальную ось
Явный вид данного равенства
ρ V g = ρ 0 V ′ g
позволяет найти отношение объемов:
Искомой величиной является доля объема тела, которая остается в воздухе, определяемая отношением:
η = V − V ′ V = 1 − V ′ V ,
где ( V − V ′) — объем тела, находящийся в воздухе.
С учетом полученного отношения ( V / V ′) искомая доля составляет
η = 1 − V ′ V = 1 − ρ ρ 0 = 1 − 1,2 ⋅ 10 3 3,0 ⋅ 10 3 = 0,6 .
Таким образом, доля объема тела, находящегося в воздухе, равна 0,6 (или 60 %).
Пример 33. Тело, имеющее массу 4,0 кг, изготовлено из материала, плотность которого равна 6,4 г/см 3 . Из внутренней части тела удаляют определенную массу материала, а образовавшуюся полость заполняют другим материалом плотностью 1,4 г/см 3 . Найти объем полости, заполнение которой материалом указанной плотности обеспечит состояние безразличного равновесия тела в жидкости плотностью 2,0 г/см 3 .
Решение . Состояние безразличного равновесия тела в жидкости означает, что тело может плавать на любой глубине; тело при этом полностью погружено в жидкость.
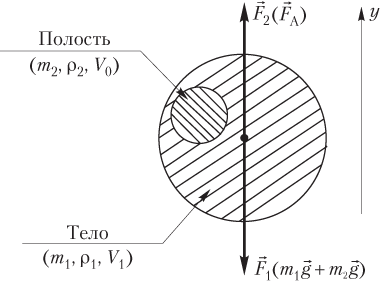
В состоянии безразличного равновесия на тело действуют две силы, показанные на рисунке:
- сила тяжести, модуль которой определяется формулой
F 1 = mg = ( m 1 + m 2 ) g ,
где m = ( m 1 + m 2 ) — масса «составного» тела; m 1 = ( M − ∆ m ) — масса тела после удаления материала из полости; M — первоначальная масса тела (указанная в условии задачи); ∆ m — масса материала, удаленного из полости; m 2 — масса материала, заполняющего полость; g — модуль ускорения свободного падения;
- сила Архимеда, модуль которой определяется формулой
F 2 = F A = ρ 0 Vg ,
где ρ 0 — плотность жидкости; V — объем тела.
Под действием указанных сил тело находится в состоянии безразличного равновесия (плавает на любой глубине); условие равновесия определяется равенством
или в проекции на вертикальную ось
В явном виде оно выглядит следующим образом:
( m 1 + m 2 ) g = ρ 0 Vg .
Преобразуем данное выражение, заменив массы произведением плотностей и объемов:
- для массы m 1 —
m 1 = M − ∆ m = M − ρ 1 V 0 ;
- для массы m 2 —
где ρ 1 — плотность материала, из которого состоит тело; ρ 2 — плотность материала, заполняющего полость; V 0 — объем полости.
Подстановка выражений, полученных для масс, в условие равновесия тела в жидкости дает равенство
M − ρ 1 V 0 + ρ 2 V 0 = ρ 0 V ,
позволяющее выразить искомую величину:
V 0 = M − ρ 0 V ρ 1 − ρ 2 .
Объем тела найдем как отношение
и подставим в полученное выражение:
V 0 = M ( 1 − ρ 0 ρ 1 ) ρ 1 − ρ 2 = M ρ 1 ρ 1 − ρ 0 ρ 1 − ρ 2 .
V 0 = 4,0 6,4 ⋅ 10 3 ⋅ 6,4 ⋅ 10 3 − 2,0 ⋅ 10 3 6,4 ⋅ 10 3 − 1,4 ⋅ 10 3 = 0,550 ⋅ 10 − 3 м 3 = 550 см 3 .
Таким образом, объем полости, обеспечивающий телу состояние безразличного равновесия в указанной жидкости, составляет 550 см 3 .
Пример 34. Прямой деревянный цилиндр плавает на поверхности воды так, что в воде находится 0,9 его высоты. На поверхность воды наливают слой масла плотностью 0,8 г/см 3 таким образом, чтобы цилиндр оказался полностью погруженным в жидкость. Какая часть высоты цилиндра окажется погруженной в воду? Плотность воды составляет 1 г/см 3 .
Решение . Рассмотрим условие равновесия цилиндра в жидкости:
- для цилиндра, плавающего в воде,
где m — масса цилиндра; g — модуль ускорения свободного падения; F A = ρ 1 g V ′ — модуль силы Архимеда, действующей на цилиндр, плавающий в воде; ρ 1 — плотность воды; V ′ — объем части цилиндра, погруженной в воду;
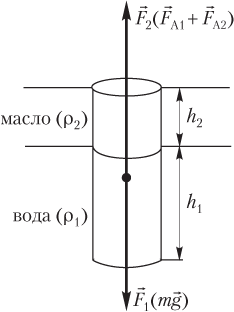
- для цилиндра, плавающего в двухслойной жидкости «вода — масло», как показано на рисунке,
где F A1 = ρ 1 gV 1 — модуль силы Архимеда, действующей на цилиндр со стороны воды; V 1 — объем части цилиндра, погруженной в воду; F A2 = ρ 2 gV 2 — модуль силы Архимеда, действующей на цилиндр со стороны масла; V 2 — объем части цилиндра, погруженной в масло.
Объемы выразим как произведение соответствующих высот на площадь поперечного сечения цилиндра S :
- для цилиндра V
- для части цилиндра, погруженной в воду V 1 ,
- для части цилиндра, погруженной в масло V 2 ,
где h — высота цилиндра; h 1 — высота части цилиндра, погруженной в воду; h 2 — высота части цилиндра, погруженной в масло.
Искомой величиной является отношение
η = h 1 h = V 1 V .
Для определения данного отношения запишем систему уравнений из условий равновесия цилиндра в воде и в двухслойной жидкости «вода — масло», подставив выражения для сил и представив массу цилиндра в виде произведения
где ρ — плотность материала цилиндра.
Указанная система имеет вид:
ρ V g = ρ 1 g V ′ ; ρ V g = ρ 1 g V 1 + ρ 2 g V 2 , >
или с учетом ( V ′/ V = 0,9):
ρ = 0,9 ρ 1 ; ρ V = ρ 1 V 1 + ρ 2 V 2 . >
Дополним систему уравнением
Подстановка первого уравнения во второе дает:
0,9 ρ 1 V = ρ 1 V 1 + ρ 2 V 2 ; V = V 1 + V 2 . >
Исключая величину V 2 , получим равенство:
ρ 1 ρ 2 ( 0,9 V − V 1 ) = V − V 1 .
Деление обеих частей равенства на V
ρ 1 ρ 2 ( 0,9 − V 1 V ) = 1 − V 1 V
позволяет найти искомую величину:
η = V 1 V = 0,9 ρ 1 − ρ 2 ρ 1 − ρ 2 = 0,9 ⋅ 1,0 ⋅ 10 3 − 0,8 ⋅ 10 3 1,0 ⋅ 10 3 − 0,8 ⋅ 10 3 = 0,5 .
Таким образом, цилиндр плавает, погрузившись в воду на половину своей высоты.
Условия плавания тел - формулы, основные принципы и положения закона Архимеда
Местоположение предмета в пространстве объясняется действующими на него силами. Нарушение баланса приложенных усилий выводит объект из равновесного состояния и даёт старт движению. В газообразной среде и жидкости вертикальный ход тела зависит от пары сил — выталкивающей и тяжести. Закон, описывающий взаимодействие двух основных составляющих, открыл Архимед за три столетия до Рождества Христова.
Физик, математик, инженер
Архимед родился в 287 году до н. э. на Сицилии в греческой колонии Сиракузы. В детстве за воспитание мальчика взялся отец — астроном и математик Фидий. Всестороннее образование юноша получил в Александрии, где занимался изучением трудов Демокрита и Евдокса, общался с Эратосфеном и Кононом. Жизнь в научной столице древнего мира сформировала Архимеда как талантливого исследователя и экспериментатора.
Учёные, повлиявшие на образование Архимеда:
- греческий филолог и географ Эратосфен — вычислил размеры Земли;
- математик и астроном Конон, составлявший прогнозы погоды и календари с указанием времени восхода и заката Солнца;
- в трудах мыслителя Демокрита разработана теория неделимой частицы — атома, которая легла в основу материалистической философии;
- малоазиатский философ Евдокс, которого считают родоначальником интегральных вычислений и теоретической астрономии.
После обучения в Египте Архимед вернулся в Сиракузы, где жил до трагической гибели в 212 году до н. э. За три года до этого римляне начали осаду сицилийского города, который помогал Карфагенскому государству. Инженерный талант греческого математика помогал горожанам сдерживать нападавшие легионы. Осаждённые греки использовали катапульты разного калибра и подъёмные краны, которые при помощи крюков переворачивали вражеские галеры. Кривые зеркала, фокусирующие лучи в одну точку, сжигали неприятельский флот.
Существует несколько вариантов легенды о гибели Архимеда. Но описания совпадают в одном — мыслителя, занятого в этот момент научными изысканиями, убил римский солдат, после того как Сиракузы сдались на милость победителя.
Архимед написал тринадцать трактатов. В книгах учёного определены основные положения гидростатики и теоретической механики. Рассчитывая площади поверхности фигур и объёмы тел, математик заложил основы интегрального и дифференциального вычисления величин. Инженерные разработки великого изобретателя находят применение и в современных конструкциях.
Тело, погружённое в жидкость
В истории науки известны примеры, когда практические запросы общества приводят к научным открытиям. Подобным образом был открыт основной закон статики. Вычисляя объём царской короны, Архимед погружал символ государственной власти в сосуд с водой. При этом учёный обратил внимание, что предмет, опущенный в жидкость, становится легче. Последующие размышления приводят великого грека к открытию гидростатического закона, названным его именем.
Закон Архимеда гласит, что на тело, погружённое в газовую среду или жидкость, действует сила, равная весу того объёма газа или жидкости, который вытеснило это тело. На языке математики постулат выражается уравнением:
Смысловое определение математических символов, использованных в формуле:
- F — выталкивающая или архимедова сила;
- g — коэффициент ускорения свободного падения, равный 9,8 м/с²;
- ρ — плотность среды, в которую помещено тело;
- V — объём вытесненной жидкости или газа.
Архимедова сила противоположна силе тяжести и всегда направлена от центра Земли строго по вертикали вверх. В невесомости, где g = 0, закон Архимеда не работает. Взаимодействие двух сил — тяжести Ft и выталкивающей Fa — определяет поведение объекта в пространстве. Наглядным примером проявления силы Архимеда является подъём пузырька воздуха к поверхности воды.
На тело, плавающее на границе сред с разными плотностями, действует суммарная сила:
где ρ₁, ρ₂, ρ₃ - плотности различных сред, а V₁, V₂, V₃ - объёмы частей предмета.
Разбирают три варианта развития событий:
- Если Ft ˂ Fa, то тело начинает всплывать.
- При условии Ft = Fa, объект пребывает в состоянии покоя.
- Если Ft ˃ Fa, то происходит погружение предмета.
Аналогичным образом развивается ситуация, если значения сил заменить величинами плотностей тела и жидкости или газа. То есть, вместо силы тяжести Ft использовать плотность предмета, а взамен выталкивающей силы Fa рассматривать плотность среды, в которую помещён объект.
Корабли не тонут, дирижабли летают
Плавучестью корабля называется способность судна оставаться в равновесном состоянии, не всплывая и не погружаясь на глубину. По закону Архимеда условия плавания тел возникают при равенстве силы тяжести выталкивающей силе. Запас плавучести определяется процентным отношением объёма водонепроницаемой полости выше ватерлинии к объёму всего корабля. Надводные суда рассчитываются с резервом плавучести не менее 50%.
Формула расчёта запаса плавучести:
где W — запас плавучести, v — объём отсеков над ватерлинией, V — объём всего корабля.
Водоизмещение является основной характеристикой водного транспорта и равно количеству воды, вытесненной подводной частью плавательного средства. Ватерлиния, являясь горизонтальным сечением, обозначается на корпусе и визуально показывает уровень нормального водоизмещения. Вычитание веса судна из водоизмещения представит грузоподъёмность транспортного средства.
В физическом смысле запас плавучести обозначает возможность находиться на поверхности водоёма. Различают нейтральную и отрицательную плавучесть. В первом случае W = 0% и судно погружено в воду до уровня палубы. Малейшее внешнее воздействие приводит к затоплению. Во втором случае корабль не способен держаться на плаву.
Предмет, находящийся в воздухе, также испытывает влияние архимедовой силы. Если подъёмная сила превышает силу тяжести, то тело начинает удаляться от поверхности земли. На этом постулате основан принцип воздухоплавания. В формуле закона Архимеда используется плотность воздуха.
Чтобы летательный аппарат поднялся, оболочку аэростата или дирижабля наполняют газом легче воздуха. Для этого подходят водород и гелий, чьи плотности меньше смеси атмосферных газов. Из-за взрывоопасности водорода чаще применяется гелий.
Идеальным вариантом считается использование в оболочке воздушного шара подогретого воздуха. Горелка устанавливается под отверстием в нижней части сферы. Периодическое включение нагревательного элемента изменяет температуру и плотность воздуха внутри шара, что позволяет регулировать скорость подъёма или спуска.
Решение примеров
Задача 1. Необходимо вычислить выталкивающую силу воды, действующую на сплошное тело цилиндрической формы объёмом 2 м³. Табличное значение плотности воды равно 1 тыс. кг/м³.
Решение. Прежде всего, определяется масса вытесненной воды:
m = ρ * V = 1000 * 2 = 2 тыс. кг.
Вес вытесненной воды, то есть архимедова сила, равны:
P = Fa = g * m = 9,8 * 2000 = 19600 Н.
Задача 2. Требуется определить количество золота в короне, изготовленной из сплава серебра и золота. Вес изделия в воздухе — 2,54 кг. Взвешивание в воде показало результат 2,34 кг.
Решение. На предмет, погружённый в воду, действует архимедова сила:
где P₁ - вес короны в воздухе, P₂ - вес драгоценности в воде, ρ — плотность воды.
Общий объём предмета складывается из объёмов золота и серебра:
где m₁ и ρ₁ - соответственно масса и плотность золота, а m₂ и ρ₂ - масса и плотность серебра.
Поскольку масса является частным от деления веса на коэффициент g, то общий объём короны можно представить формулой:
V = m₁/ρ₁ + 1/ρ₂ * (P₁/g — m₁),
где выражение (P₁/g — m₁) = m₂.
Значение объёма V подставляется в уравнение закона Архимеда:
Fa = g * ρ * (m₁/ρ₁ + 1/ρ₂ * (P₁/g — m₁)) = P₁ - P₂.
Путём математических преобразований определяется m₁:
m₁ = (P₁* (1 — ρ/ρ₂) — P₂)/(g * ρ * (1/ρ₁ - 1/ρ₂)).
Подставив числовые значения коэффициентов и веса короны, получаем ответ: m₁ = 985 г
О существовании трактатов Архимеда европейцам стало известно в XII веке. В это время с арабского языка переводятся труды мусульманских учёных, досконально изучивших работы древнегреческого математика. В XVI столетии методы великого исследователя природы использовал Галилей. Открытия, сделанные Архимедом, послужили фундаментом для развития средневековой механики.
Читайте также: