Тело находящееся в газе плавает на каком рисунке
Физика
На тело, погруженное в жидкость (или газ), действует выталкивающая сила — сила Архимеда .
- численно равна весу жидкости, вытесненной телом:
где ρ 0 — плотность жидкости (или газа); g — модуль ускорения свободного падения; V ′ — объем погруженной в жидкость (или газ) части тела;
- направлена вертикально вверх;
- приложена к центру тяжести жидкости (или газа), которая заполняла бы объем, занятый погруженным в нее телом (т.е. к центру тяжести вытесненной жидкости).
Сила Архимеда представляет собой равнодействующую сил давления, действующих со стороны жидкости (или газа) на помещенное в нее (в него) тело.
Подъемная сила — это равнодействующая силы тяжести m g → и силы Архимеда F → А :
F → под = F → А + m g → ,
где F → А — сила Архимеда; m g → — сила тяжести; m — масса тела; g → — ускорение свободного падения.
Величина подъемной силы определяется разностью:
Если величина подъемной силы
- положительная, то тело плавает на поверхности жидкости, частично погружаясь в нее;
- отрицательная — тело тонет ;
- равна нулю — тело находится в состоянии безразличного равновесия (плавает на любой глубине).
Условием плавания тела в жидкости (или газе) является равенство модулей силы Архимеда и силы тяжести:
где F A = ρ 0 gV ′ — модуль силы Архимеда; ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; V ′ — объем погруженной в жидкость части тела; mg — модуль силы тяжести; m = ρ т V т — масса тела; ρ т — плотность тела; V т — объем тела.
Сила Архимеда определяется произведением:
где ρ 0 — плотность жидкости (или газа); V ′ — объем погруженной в жидкость (или газ) части тела;
Сила тяжести определяется также произведением:
где ρ т — плотность тела; V т — объем тела.
Тело может плавать не только на поверхности жидкости, но и на любой глубине (то есть погрузившись полностью).
- ρ т < ρ 0 (плотность тела меньше плотности жидкости), то тело плавает на поверхности жидкости;
- ρ т > ρ 0 (плотность тела больше плотности жидкости), то тело тонет ;
- ρ т = ρ 0 (плотность тела равна плотности жидкости), то тело плавает на любой глубине — состояние безразличного равновесия .
Пример 32. Некоторое тело обладает плотностью 1,2 г/см 3 . Если поместить его в жидкость, имеющую плотность 3,0 г/см 3 , то оно будет плавать на ее поверхности. Определить, какая часть плавающего тела при этом находится в воздухе.
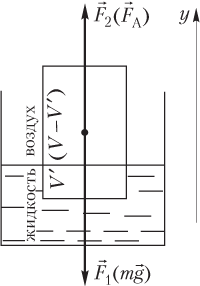
Решение . На тело, плавающее в жидкости, действуют две силы, показанные на рисунке:
- сила тяжести, модуль которой определяется формулой
где m = ρ V — масса тела; ρ — плотность тела; V — объем тела; g — модуль ускорения свободного падения;
- сила Архимеда, модуль которой определяется формулой
F 2 = F A = ρ 0 V ′ g ,
где ρ 0 — плотность жидкости; V ′ — объем погруженной в жидкость части тела.
Под действием указанных сил тело находится в равновесии (плавает); условие равновесия определяется равенством
или в проекции на вертикальную ось
Явный вид данного равенства
ρ V g = ρ 0 V ′ g
позволяет найти отношение объемов:
Искомой величиной является доля объема тела, которая остается в воздухе, определяемая отношением:
η = V − V ′ V = 1 − V ′ V ,
где ( V − V ′) — объем тела, находящийся в воздухе.
С учетом полученного отношения ( V / V ′) искомая доля составляет
η = 1 − V ′ V = 1 − ρ ρ 0 = 1 − 1,2 ⋅ 10 3 3,0 ⋅ 10 3 = 0,6 .
Таким образом, доля объема тела, находящегося в воздухе, равна 0,6 (или 60 %).
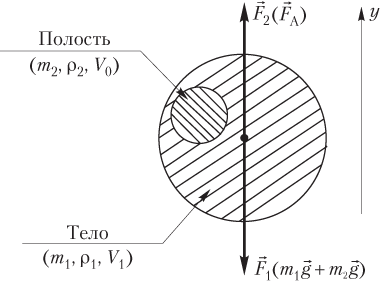
Пример 33. Тело, имеющее массу 4,0 кг, изготовлено из материала, плотность которого равна 6,4 г/см 3 . Из внутренней части тела удаляют определенную массу материала, а образовавшуюся полость заполняют другим материалом плотностью 1,4 г/см 3 . Найти объем полости, заполнение которой материалом указанной плотности обеспечит состояние безразличного равновесия тела в жидкости плотностью 2,0 г/см 3 .
Решение . Состояние безразличного равновесия тела в жидкости означает, что тело может плавать на любой глубине; тело при этом полностью погружено в жидкость.
В состоянии безразличного равновесия на тело действуют две силы, показанные на рисунке:
- сила тяжести, модуль которой определяется формулой
F 1 = mg = ( m 1 + m 2 ) g ,
где m = ( m 1 + m 2 ) — масса «составного» тела; m 1 = ( M − ∆ m ) — масса тела после удаления материала из полости; M — первоначальная масса тела (указанная в условии задачи); ∆ m — масса материала, удаленного из полости; m 2 — масса материала, заполняющего полость; g — модуль ускорения свободного падения;
- сила Архимеда, модуль которой определяется формулой
F 2 = F A = ρ 0 Vg ,
где ρ 0 — плотность жидкости; V — объем тела.
Под действием указанных сил тело находится в состоянии безразличного равновесия (плавает на любой глубине); условие равновесия определяется равенством
или в проекции на вертикальную ось
В явном виде оно выглядит следующим образом:
( m 1 + m 2 ) g = ρ 0 Vg .
Преобразуем данное выражение, заменив массы произведением плотностей и объемов:
- для массы m 1 —
m 1 = M − ∆ m = M − ρ 1 V 0 ;
- для массы m 2 —
где ρ 1 — плотность материала, из которого состоит тело; ρ 2 — плотность материала, заполняющего полость; V 0 — объем полости.
Подстановка выражений, полученных для масс, в условие равновесия тела в жидкости дает равенство
M − ρ 1 V 0 + ρ 2 V 0 = ρ 0 V ,
позволяющее выразить искомую величину:
V 0 = M − ρ 0 V ρ 1 − ρ 2 .
Объем тела найдем как отношение
и подставим в полученное выражение:
V 0 = M ( 1 − ρ 0 ρ 1 ) ρ 1 − ρ 2 = M ρ 1 ρ 1 − ρ 0 ρ 1 − ρ 2 .
V 0 = 4,0 6,4 ⋅ 10 3 ⋅ 6,4 ⋅ 10 3 − 2,0 ⋅ 10 3 6,4 ⋅ 10 3 − 1,4 ⋅ 10 3 = 0,550 ⋅ 10 − 3 м 3 = 550 см 3 .
Таким образом, объем полости, обеспечивающий телу состояние безразличного равновесия в указанной жидкости, составляет 550 см 3 .
Пример 34. Прямой деревянный цилиндр плавает на поверхности воды так, что в воде находится 0,9 его высоты. На поверхность воды наливают слой масла плотностью 0,8 г/см 3 таким образом, чтобы цилиндр оказался полностью погруженным в жидкость. Какая часть высоты цилиндра окажется погруженной в воду? Плотность воды составляет 1 г/см 3 .
Решение . Рассмотрим условие равновесия цилиндра в жидкости:
- для цилиндра, плавающего в воде,
где m — масса цилиндра; g — модуль ускорения свободного падения; F A = ρ 1 g V ′ — модуль силы Архимеда, действующей на цилиндр, плавающий в воде; ρ 1 — плотность воды; V ′ — объем части цилиндра, погруженной в воду;
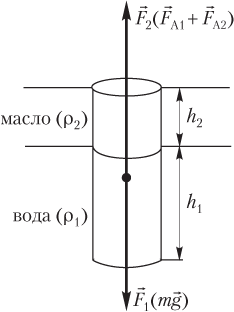
- для цилиндра, плавающего в двухслойной жидкости «вода — масло», как показано на рисунке,
где F A1 = ρ 1 gV 1 — модуль силы Архимеда, действующей на цилиндр со стороны воды; V 1 — объем части цилиндра, погруженной в воду; F A2 = ρ 2 gV 2 — модуль силы Архимеда, действующей на цилиндр со стороны масла; V 2 — объем части цилиндра, погруженной в масло.
Объемы выразим как произведение соответствующих высот на площадь поперечного сечения цилиндра S :
- для цилиндра V
- для части цилиндра, погруженной в воду V 1 ,
- для части цилиндра, погруженной в масло V 2 ,
где h — высота цилиндра; h 1 — высота части цилиндра, погруженной в воду; h 2 — высота части цилиндра, погруженной в масло.
Искомой величиной является отношение
η = h 1 h = V 1 V .
Для определения данного отношения запишем систему уравнений из условий равновесия цилиндра в воде и в двухслойной жидкости «вода — масло», подставив выражения для сил и представив массу цилиндра в виде произведения
где ρ — плотность материала цилиндра.
Указанная система имеет вид:
ρ V g = ρ 1 g V ′ ; ρ V g = ρ 1 g V 1 + ρ 2 g V 2 , >
или с учетом ( V ′/ V = 0,9):
ρ = 0,9 ρ 1 ; ρ V = ρ 1 V 1 + ρ 2 V 2 . >
Дополним систему уравнением
Подстановка первого уравнения во второе дает:
0,9 ρ 1 V = ρ 1 V 1 + ρ 2 V 2 ; V = V 1 + V 2 . >
Исключая величину V 2 , получим равенство:
ρ 1 ρ 2 ( 0,9 V − V 1 ) = V − V 1 .
Деление обеих частей равенства на V
ρ 1 ρ 2 ( 0,9 − V 1 V ) = 1 − V 1 V
позволяет найти искомую величину:
η = V 1 V = 0,9 ρ 1 − ρ 2 ρ 1 − ρ 2 = 0,9 ⋅ 1,0 ⋅ 10 3 − 0,8 ⋅ 10 3 1,0 ⋅ 10 3 − 0,8 ⋅ 10 3 = 0,5 .
Таким образом, цилиндр плавает, погрузившись в воду на половину своей высоты.
Сила Архимеда
В древней Греции примерно за 250 лет до нашей эры жил выдающийся ученый – Архимед. Он заметил, что если в жидкость поместить какое-либо тело, то жидкость будет это тело выталкивать. Газ, аналогично жидкости, выталкивает тела, помещенные в него.
Сила Архимеда – это сила, с которой жидкость, или газ, выталкивают погруженное в них тело.
Архимед сумел рассчитать, что выталкивающая сила равна весу жидкости (или газа), в погруженном объеме тела.
Благодаря выталкивающей силе летают воздушные шары и дирижабли, плавают корабли и подводные лодки.
Формула для расчета выталкивающей силы
Рассмотрим тело, погруженное в емкость, наполненную жидкостью (рис. 1). На рисунке серым закрашена часть объема, находящаяся внутри жидкости. Тело погрузилось на величину \(\Delta h\) и находится в равновесии, на него действуют две силы – выталкивающая и сила тяжести.
Силу Архимеда можно вычислить с помощью такого выражения:
\( F_ <А>\left( H \right) \) – сила, с которой жидкость или газ выталкивает погруженное тело;
\( \displaystyle \rho_<\text<ж>> \left(\frac<\text<кг>><\text<м>^<3>> \right) \) – плотность жидкости (или газа), в которую тело погружено;
\( \displaystyle g \left(\frac<\text<м>>
\( V_<\text<погр>> \left(\text<м>^ <3>\right) \) – та часть объема тела, которая погружена в жидкость.
Чтобы получить правильный результат, в формулу для силы Архимеда объем нужно подставлять в кубометрах. Читайте о том, как переводить объем в единицы системы СИ.
Условия плавания тел
На рисунке 2 представлены несколько вариантов для тела, погруженного в жидкость.
Рисунок 2а – тело плавает на поверхности, частично погрузившись в жидкость. На рисунке 2б тело плавает внутри жидкости, а на рисунке 2в – тело лежит на дне.
Во всех случаях на тело действует сила тяжести и выталкивающая сила.
С помощью векторных уравнений ответим на вопрос, почему одни тела плавают, а другие – нет.
Составляя силовые уравнения, заметим, что для случаев, когда тело плавает на поверхности (рис. 2а), или в объеме жидкости (рис. 2б), сила тяжести уравновешивается силой Архимеда.
А для случая, когда тело лежит на дне (рис. 2в), сила тяжести больше выталкивающей силы на величину реакции опоры \(\vec
Преобразуем силу тяжести \( F_<\text<тяж>> \)
Масса и объем тела связаны через его плотность.
Выражаем из этого уравнения массу
Заменив массу тела его объемом и плотностью, для силы тяжести можно записать:
Поставим это выражение в уравнения для случаев, когда тело плавает (рис 2а и рис 2б):
Можно разделить обе части полученного уравнения на ускорение свободного падения
Так как в случае рисунка 2а, погруженный объем меньше объема тела, то
Для рисунка 2б, на котором тело погружено полностью, плотности тела и жидкости совпадают:
Тело лежит на дне (рис. 2в), когда плотность тела превышает плотность той жидкости, в которую оно погружено:
Выводы о плавании
На поверхности (рис. 2а) тело плавает, когда его плотность меньше плотности жидкости:
В объеме (внутри) жидкости (рис. 2б) тело плавает, когда плотности тела и жидкости совпадают:
Тело тонет и лежит на дне (рис. 2в), когда плотность тела больше плотности жидкости:
Тело находящееся в газе плавает на каком рисунке

Давненько пользуемся мы этими учебниками.
Еще наши мамы и папы по ним учились.
Как же осилить домашнее задание, ответить на вопросы и решить задачи в упражнениях?
Уверена, что думающие ученики сначала всё сделают сами, а эти сведения будут помощью «застрявшим в пути».
Ответы на ДЗ по физике помогут вам проверить себя и найти ошибки.
Ответы на ДЗ из упражнений соответствуют всем выпускам учебников этого автора, начиная с 1989 г.
Так как номера упражнений с одинаковыми вопросами в разных выпусках различаются, ответы на вопросы к упражнениям скомпонованы по темам.
На этой странице представлены решения задач по параграфам: Плавание тел.
Заодно некоторые узнают, какую тему по физике они сейчас изучают))
Так нет ли здесь нужной вам задачи?
Обязательно найдется!
1. На весах уравновесили отливной сосуд с водой. В воду опустили деревянный брусок. Равновесие весов вначале нарушилось. Но когда вся вода, вытесненная плавающим бруском, вытекла из сосуда, равновесие весов востановилось. Объясните это явление.

Когда в воду опустили брусок, равновесие нарушилось, поскольку на чашку весов стал действовать еще и вес бруска.
Однако брусок при частичном погружении в воду вытеснил какое-то количество воды из чаши.
Брусок вытеснил объем воды, равный объему погруженной в нее части бруска.
А вес вытесненной при этом воды равен весу всего бруска в воздухе.
Когда вся вытесненная бруском вода вылилась из чаши, снова установилось равновесие весов.
2. Почему плавает тяжелое судно, а гвоздь, упавший вводу тонет?
Корабль с грузом на плаву, т.е.частично погруженный в воду, вытесняет своей погруженной частью какое-то количество воды.
Чтобы корабль с грузом плавал, надо, чтобы вес корабля с грузом в воздухе был меньше веса вытесненной им воды (т.е. меньше архимедовой силы, действующей на корабль).
Если вес корабля с грузом в воздухе будет больше веса вытесненной им воды, то корабль утонет.
При конструировании корабля обязательно учитывают это условие плавания.
У железного гвоздя вес его в воздухе оказывается больше веса вытесненной им воды.
Поэтому гвоздь тонет.
Иначе, но тоже правильно:
Условие плавания тел в жидкости: если плотность тела меньше плотности жидкости, то оно всплывает и будет плавать на поверхности.
Значит, надо сравнивать плотности корабля и воды.
Но в этом условии речь идет о сплошных телах.
Но корабль тело не сплошное.
Весь объем корабля занимают обычно металлические части корпуса, груз и воздушные пустоты, поэтому говорят о средней плотности.
При строительстве корабля и погрузке на него грузов закладывается условие: сделать так,чтобы средняя плотность корабля с грузом была меньше плотности воды.
Чем меньше средняя плотность корабля по сравнению с плотностью воды, тем меньше его осадка, т.е. тем меньше он погружен в воду.
А плотность сплошного железного гвоздя больше плотности воды, поэтому он тонет.
Если бы корабль был сделан целиком из железа, то он тоже бы тонул.
3. На рисунке изображено одно и то же тело, плавающее в двух разных жидкостях. Плотность какой жидкости больше? Почему?
Что можно сказать о силе тяжести, действующей на тело, и архимедовой силе в том и другом случае?

Тело одно и то же.
Чем меньше плотность тела по сравнению с плотностью жидкости, тем меньшая часть тела погружена в жидкость.
В первом сосуде тело погружено в жидкость больше, чем во втором.
Значит, плотность первой жидкости меньше, чем второй.
Сила тяжести, действующая на тело в обоих случаях одинакова.
Архимедова сила, действующая на погруженное тело, зависит от плотности жидкости.
Архимедова сила, действующая на погруженное тело, больше там, где больше плотность жидкости, т.е. во втором сосуде.
4. Яйцо (или картофелина) тонет в пресной воде, но плавает в соленой. Объясните почему. Пронаблюдайте это сами на опыте.
Условие плавания тел: если плотность тела меньше (или равно) плотности жидкости, тело плавает на поверхности (или внутри нее).
Плотность соленой воды больше, чем плотность пресной воды.
Яйцо (или картофелина) тонет в пресной воде, значит плотность яйца (или картофелины) больше плотности пресной воды.
Яйцо (или картофелина) плавает в соленой воде, значит плотность яйца (или картофелины) меньше плотности соленой воды.
5. Изобразите графически силы, действующие на тело, плавающее на воде, всплывающее на поверхность воды, тонущее в воде.

6. Пользуясь таблицами плотности, определите, какие металлы будут плавать в ртути, а какие - тонуть.
Плавать в ртути будут металлы, плотность которых меньше плотности ртути:
свинец, серебро, медь, латунь, железо.
Тонуть в ртути будут металлы, плотность которых больше плотности ртути:
осмий, иридий, платина, золото.
7. Будет ли кусок льда плавать в бензине, керосине, глицерине?
Плотность льда = 900 кг/м 3 .
Лед будет плавать в жидкостях с большей плотностью: глицерин (1260) -нет значений плотности для глицерина в учебнике!
Лед будет тонуть в жидкостях с меньшей плотностью: бензин (710), керосин (800).
Гидростатика
На рисунке представлены графики зависимости давления \(p\) от глубины погружения \(h\) для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре. 
Выберите два верных утверждения, согласующихся с приведёнными графиками.
1) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
2) Плотность керосина 0,82 г/см \(^3\) , аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
3) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
4) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
5) Плотность оливкового масла 0,92 г/см \(^3\) , аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Полное давление \(p\) складывается из атмосферного давления \(p_a\) и гидростатического давления столба жидкости: \[p=\rho gh+p_a\] 1) Как видно из графика, давление воды на глубине 10 м принимает значение 200 кПа, что в два раза больше атмосферного давления (Атмосферное давление 100 кПа).
Утверждение 1 – \(\color
2) Так как плотность керосина меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 2 – \(\color
3) Давление в воде на глубине 25 м равно 350 кПа, что в 3,5 раза больше атмосферного.
Утверждение 3 – \(\color
4) Так как прямая давления в дийодметане лежит выше прямой давления в воде, то это означает, что давление в дийодметане возрастает быстрее, чем в воде.
Утверждение 4 – \(\color
5) Так как плотность оливкого масла меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 5 – \(\color
К телу, имеющему внутреннюю герметичную полость, на невесомой нерастяжимой нити привязан сплошной шарик. Система «тело + шарик» плавает в сосуде с жидкостью, не касаясь стенок и дна сосуда. Плотность материала тела и шарика 1,6 г/см \(^3\) , плотность жидкости 800 кг/м \(^3\) , объём полости составляет 3/4 объёма тела, объём шарика равен 1/4 объёма тела. Исходя из условия задачи, выберите два верных утверждения.
1) Модуль силы Архимеда, действующей на тело, меньше модуля силы Архимеда, действующей на шарик.
2) Модуль силы натяжения нити равен модулю силы тяжести, действующей на шарик.
3) Модуль силы натяжения нити меньше модуля силы Архимеда, действующей на тело.
4) Модуль силы тяжести, действующей на шарик, равен модулю силы тяжести, действующей на тело.
5) Объём погружённой части тела равен четверти объёма этого тела.

Запишем первый закон Ньютона для тела и шарика: \[F_<\text<Арх Т>>-m_<\text<Т>>g-T=0\] \[F_<\text<Арх Ш>>-m_<\text<Ш>>g+T=0\]
Сложим два уравнения: \[F_<\text<Арх Т>>-m_<\text<Т>>g+F_<\text<Арх Ш>>-m_<\text<Ш>>g=0\]
Обозначим плотность жидкости \(\rho_1\) , плотность материала \(\rho_2=2\rho_1\) \[\rho_1gV_1-\rho_2\cdot \frac<1><4>V_
Тело плавает, погруженное на 3/4 своего объёма.
1) Сила Архимеда, действующая на тело, равна \(\displaystyle F_<\text<Арх Т>>=\rho_1g\frac<3><4>V_T\) , а сила Архимеда, действующая на шар \(\displaystyle F_<\text<Арх Т>>=\rho_1g\frac<1><4>V_T\) .
Утверждение 1 – \(\color
2) \[T=m_<\text<Ш>>g-F_<\text<Арх Ш>>\]
Утверждение 2 – \(\color
3) \[T=F_<\text<Арх Т>>-m_<\text<Т>>g\]
Утверждение 3 – \(\color
4) Модуль силы тяжести тела: \[m_<\text<Т>>g=\rho_2\cdot \frac<1><4>V_
Утверждение 4 – \(\color
5) Объём погружённой части тела равен \(\dfrac<3><4>\) объёма этого тела.
Утверждение 5 – \(\color
Ученик помещал цилиндр, не удерживая его, в различные жидкости, плотности которых представлены в таблице, и измерял объем погруженной в жидкость части цилиндра \(V_\text< погр>\) . По результатам измерений он получил зависимость, представленную на графике объема погруженной части цилиндра \(V_\text<погр>\) от плотности жидкости \(\rho\) . Объем цилиндра постоянен и равен \(V=10\) см \(^3\)
1) В бензине и в спирте цилиндр погружен на одинаковый объем. В таком случае сила Архимеда равна \[F_A=\rho gV_\text<погр>,\] где \(\rho\) – плотность жидкости, в которую погружено тело.
Но плотность спирта больше плотности бензина, а значит и сила Архимеда, действущая на цилиндр в спирте, больше силы Архимеда, действующей на цилиндр в бензине.
Утверждение 1 – \(\color
2) Цилиндр тонет при плотности меньше, чем 1 г/см \(^3\) , у глицирина плотность 1,26 г/см \(^3\) , значит, цилиндр плавает.
Утверждение 2 – \(\color
3) У бромоформа плотность больше 1 г/см \(^3\) , а значит сила Архимеда уравновешивает силу тяжести.
По графику видим, что цилиндр начинает плавать при плотности жидкости 1г/см \(^3\) , а значит именно такова плотность материала, из которого он сделан. Откуда сила Архимеда, действующая на цилиндр \[F_A=mg=1\text< г/см$^3$>\cdot 10\text< см$^3$>\cdot 10\text< Н/кг>=100\text< мН>\] Утверждение 3 – \(\color
4) Нет, при плотности меньше 1 г/см3 цилиндр не плавает.
Утверждение 4 – \(\color
5) У глицирина и бромоформа плотность больше 1 г/см \(^3\) , а значит сила Архимеда уравновешивает силу тяжести и силы Архимеда одинаковы.
На полу лифта расположены два одинаковых металлических бака, в которых доверху налита вода (см. рисунок). 
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Давление воды на дно первого бака в 4 раза меньше, чем на дно второго.
2) Первый бак давит на пол лифта с силой, в 2 раза меньшей, чем второй.
3) Сила давления воды на дно первого бака в 2 раза меньше, чем на дно второго.
4) Первый бак оказывает на пол лифта в 2 раза меньшее давление, чем второй.
5) Если лифт начнёт движение вниз с ускорением 2 м/с \(^2\) , давление воды на дно баков уменьшится на 20 %.
В сосуд с жидкостью погружают маленький датчик манометра, который регистрирует давление, создаваемое только столбом жидкости (без учёта атмосферного давления). На рисунке представлен график зависимости показаний \(p\) этого датчика давления от времени \(t\) . Известно, что датчик может либо двигаться строго по вертикали вниз со скоростью 1 мм/с, либо покоиться. 
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) Максимальная глубина погружения датчика давления равна 20 см.
2) В промежутке времени от 50 с до 150 с датчик давления находился на одной и той же глубине.
3) Плотность жидкости, в которую опустили датчик давления, равна 650 кг/м \(^3\) .
4) Максимальная глубина погружения датчика давления равна 15 см.
5) Плотность жидкости, в которую опустили датчик давления, равна 1300 кг/м \(^3\) .
Гениальный учёный Архимед, живший в древнегреческих Сиракузах в III веке до нашей эры, прославился среди современников как создатель оборонительных машин, способных перевернуть боевой корабль. Другое его изобретение, «Архимедов винт», по сей день остаётся важнейшей деталью гигантских буровых установок и кухонных мясорубок. Мир обязан Архимеду революционными открытиями в области оптики, математики и механики. Его личность окутана легендами, порой весьма забавными. С одной из них мы и начнём нашу статью. Однажды царь Сиракуз Гиерон II обратился к Архимеду с просьбой установить, действительно ли его корона выполнена из чистого золота, как утверждал ювелир. Правитель подозревал, что мастер прикарманил часть драгоценного металла и частично заменил его серебром. В те времена не существовало способов определить химический состав металлического сплава. Задача поставила учёного в тупик. Размышляя над ней, он отправился в баню и лёг в ванну, до краёв наполненную водой. Когда часть воды вылилась наружу, на Архимеда снизошло озарение. Такое, что учёный голышом выскочил на улицу и закричал «Эврика!», что по-древнегречески означает «Нашёл!». Он предположил, что вес вытесненной воды был равен весу его тела, и оказался прав. Явившись к царю, он попросил принести золотой слиток, равный по весу короне, и опустить оба предмета в наполненные до краёв резервуары с водой. Корона вытеснила больше воды, чем слиток. При одной и той же массе объём короны оказался больше, чем объём слитка, а значит, она обладала меньшей плотностью, чем золото. Выходит, царь правильно подозревал своего ювелира. Так был открыт принцип, который теперь мы называем законом Архимеда: Эта выталкивающая сила и называется силой Архимеда. На любой объект, погружённый в воду, действует выталкивающая сила, равная весу вытесненной им жидкости. Таким образом, вес объекта, погружённого в воду, будет отличаться от его веса в воздухе в меньшую сторону. Разница будет равна весу вытесненной воды. Чем больше плотность среды — тем меньше вес. Именно поэтому погрузившись в воду, мы можем легко поднять другого человека. Выталкивающая сила зависит от трёх факторов: Сопоставив эти данные, получаем формулу: Поскольку сила Архимеда, действующая на тело, зависит от объёма его погружённой части и плотности среды, в которой оно находится, можно рассчитать, как поведёт себя то или иное тело в определённой жидкости или газе. Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности. Если плотности тела и жидкости или газа равны — тело будет находиться в безразличном равновесии в толще жидкости или газа. Если плотность тела больше, чем плотность жидкости или газа, — оно уйдёт на дно. Корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Но если корабль получит пробоину и пространство внутри заполнится водой, то общая плотность судна увеличится, и оно утонет. В подводных лодках существуют специальные резервуары, заполняемые водой или сжатым воздухом в зависимости от того, нужно ли уйти на глубину или подняться ближе к поверхности. Тот же самый принцип используют рыбы, наполняя воздухом специальный орган — плавательный пузырь. На тело, плотно прилегающее ко дну, выталкивающая сила не действует. Это учитывают при подъёме затонувших кораблей. Сначала судно слегка приподнимают, позволяя воде проникнуть под него. Тогда давление воды начинает действовать на корабль снизу. Но чтобы поднять корабль на поверхность, необходимо уменьшить его плотность. Разумеется, воздух в получившем пробоину корпусе не удержится. Поэтому его заполняют каким-нибудь лёгким веществом, например, шариками пенополистирола. Примечательно, что эта идея впервые пришла в голову не учёным, а авторам диснеевского комикса, в котором Дональд Дак таким образом поднимает со дна яхту Скруджа Макдака. Датский инженер Карл Кройер (Karl Krøyer), впервые применивший метод на практике, по собственному признанию вдохновлялся «Утиными историями». В воздухе архимедова сила действует так же, как в жидкости. Но поскольку плотность воздуха обычно намного меньше, чем плотность окружённых им предметов, выталкивающая сила оказывается ничтожно мала. Впрочем, есть исключения. Воздушный шарик, наполненный гелием, стремится вверх именно потому, что плотность гелия ниже, чем плотность воздуха. А если наполнить шар обычным воздухом — он упадёт на землю. Плотность воздуха в нём будет такая же, как у воздуха снаружи, но более высокая плотность резины обеспечит падение шарика. Этот принцип используется в аэростатах — воздушные шары и дирижабли наполняют гелием или горячим воздухом (чем горячее воздух, тем ниже его плотность), чтобы подняться, и снижают концентрацию гелия (или температуру воздуха), чтобы спуститься. На них действует та же выталкивающая сила, что и на подводные лодки. Именно поэтому перемещения на аэростатах называют воздухоплаванием. При выполнении заданий 2–5, 8, 11–14, 17–18 и 20–21 в поле ответа запишите одну цифру, которая соответствует номеру правильного ответа. Ответом к заданиям 1, 6, 9, 15, 19 является последовательность цифр. Запишите эту последовательность цифр. Ответы к заданиям 7, 10 и 16 запишите в виде числа с учетом указанных в ответе единиц. Для каждого понятия из первого столбца подберите соответствующий пример из второго столбца. На рисунке точками на линейках показаны положения четырёх тел, причём для тел 1 и 2 положения отмечались через каждую секунду, а для тел 3 и 4 — через каждые 2 с. Наименьшую среднюю скорость движения имеет тело После удара бильярдный шар массой 125 г катится со скоростью 0,8 м/с и сталкивается с другим неподвижным шаром такой же массы. Определите суммарный импульс шаров после соударения. 4) не хватает данных для решения задачи При движении материальной точки по окружности модуль её скорости не меняется, следовательно. 1) равнодействующая сила, приложенная к материальной точке, равна нулю 2) материальная точка совершает равномерное движение 3) материальная точка движется в неинерциальной системе отсчёта 4) ускорение материальной точки равно нулю Чемодан сначала положили на пол, а затем поставили на полку. Сравните давление (р1 и p2) и силу давления (F1 и F2) чемодана, соответственно, на пол и на полку. Груз, подвешенный к динамометру, равномерно опускают в сосуд с водой до полного погружения груза. Как в процессе погружения изменяется сила упругости, действующая на груз, а также давление воды на дно сосуда? Для каждой величины определите соответствующий характер изменения: 3) не изменяется Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
1) Датчик двигался на промежутках от 0 с до 50 с и от 150 с до 200 с, т. е. глубина погружения \(h=1 \cdot (50 + 50 ) = 100\) мм \(= 10\) см.
Утверждение 1 – \(\color
2) Из графика видно, что давление не изменяется в промежутке времени от 50 с до 150 с, это означает что датчик находился на одной и той же глубине, т. е. покоился.
Утверждение 2 – \(\color
3) Давление столба жидкости: \[p=\rho gh\] Плотность жидкости: \[\rho=\frac
Утверждение 3 – \(\color
4) Глубина погружения 10 см
Утверждение 4 – \(\color
5) Плотность жидкости \(\rho=1300\) кг/м \(^3\)
Утверждение 5 – \(\colorАрхимедова сила: что это такое и как действует
«Эврика!» Открытие закона Архимеда

На тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа в объёме погружённой части тела.
Формула силы Архимеда

Как действует сила Архимеда

Сила Архимеда в жидкости: почему корабли не тонут

Сила Архимеда в газах: почему летают дирижабли
Вариант 6
Прибор Физические величины А) ареометр 1) плотность жидкости Б) мензурка 2) давление внутри жидкости В) манометр 3) температура жидкости 4) объем жидкости 5) масса жидкости 

Сила упругости Давление
На коротком плече рычага укреплён груз массой 50 кг. Для того чтобы поднять груз на высоту 4 см, к длинному плечу рычага приложили силу, равную 100 Н. При этом точка приложения этой силы опустилась на 25 см. Определите КПД рычага.
В каких агрегатных состояниях вещества при увеличении его температуры увеличивается средняя скорость теплового движения молекул?
1) только в газах
2) только в жидкостях
3) в газах и жидкостях
4) в газах, жидкостях и твёрдых телах
На рисунке изображены графики зависимости изменения температуры от времени двух тел одинаковой массы. Первоначально тела находились в твёрдом состоянии.
Выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) Теплоёмкость первого тела в твёрдом состоянии больше, чем теплоёмкость второго тела в твёрдом состоянии.
2) Температура плавления первого тела меньше, чем второго.
3) Удельная теплота плавления первого тела больше второго.
4) В конечный момент времени температура тел одинакова.
5) Удельная теплоёмкость первого тела в жидком состоянии меньше, чем у второго тела в жидком состоянии.
В калориметре смешали по 100 г воды, взятой при температуре 40 °С и 100 °С, и добавили по 50 г воды при температуре 60 °С и 80 °С. Какова температура смеси после установления равновесия?
К заряженному электроскопу поднесли, не касаясь, заряженную палочку. При этом лепестки электроскопа расходятся на больший угол. Какое из утверждений верно?

1) Палочка и электроскоп имеют одинаковый по знаку заряд.
2) Палочка и электроскоп имеют противоположный по знаку заряд.
3) Заряд с палочки переходит на электроскоп.
4) Заряд с электроскопа переходит на палочку.
Чему равно общее сопротивление участка цепи, изображенного на рисунке, если R1 = 1 Ом, R2 = 10 Ом, R3 = 10 Ом, R4 = 5 Ом?

На рисунке показана вольт-амперная характеристика некоторого резистора. Каково сопротивление резистора?

На линзу падает луч, показанный на рисунке. Ходу луча после преломления в линзе соответствует линия
Луч света падает на плоское зеркало под углом 30°. Как изменятся угол падения луча и угол между отражённым лучом и зеркалом, если зеркало повернуть на угол 10° так, как показано на рисунке?

Для каждой физической величины определите соответствующий характер изменения:
| Угол падения | Угол между отражённым лучом и зеркалом |
Какую силу тока показывает амперметр?

Ядро аргона содержит
1) 40 протонов и 22 нейтрона
2) 40 протонов и 18 нейтронов
3) 18 протонов и 40 нейтронов
4) 18 протонов и 22 нейтрона
В таблице представлены данные по исследованию зависимости атмосферного давления и температуры кипения воды от высоты местности относительно уровня моря.

Какое утверждение является верным?
1) При уменьшении высоты над уровнем моря атмосферное давление уменьшается.
2) Температура кипения воды прямо пропорциональна атмосферному давлению.
3) Атмосферное давление обратно пропорционально высоте местности относительно уровня моря.
4) При уменьшении атмосферного давления температура кипения воды уменьшается.
Для изготовления резисторов использовался рулон нихромовой проволоки. Поочередно в цепь включали отрезки проволоки длиной 4 м, 8 м и 12 м. Для каждого случая измерялись напряжение на резисторе и силу тока в цепи.
| L, м (длина проволоки) | U, В | I, А |
| 4 | 9 | 6 |
| 8 | 9 | 3 |
| 12 | 9 | 2 |
Какой вывод можно сделать на основании проведенных исследований?
1) сопротивление проводника обратно пропорционально площади его поперечного сечения
2) сопротивление проводника прямо пропорционально его длине
3) сопротивление проводника зависит от силы тока в проводнике
4) сопротивление проводника зависит от напряжения на концах проводника
5) сила тока в проводнике обратно пропорциональна его сопротивлению
Люминесценцией называется нетепловое излучение тел. Среди люминесцентных явлений выделяют фотолюминесценцию: свечение некоторых веществ при их освещении внешним электромагнитным излучением. Фотолюминесценция отличается важной особенностью: свет люминесценции имеет иной спектральный состав, чем свет, вызвавший свечение. Все наблюдения показывают, что свет люминесценции характеризуется большей длиной волны, чем возбуждающий свет. Некоторые тела сохраняют способность светиться некоторое время после того, как освещение их прекратилось. Такое послесвечение может иметь различную длительность: от долей секунды до многих часов. Свечение, прекращающееся с освещением, называют флюоресценцией, а свечение, имеющее заметную длительность, — фосфоресценцией.
Другой пример люминесценции — хемилюминесценция, т.е. свечение тел при протекании химической реакции. Хемилюминесценция связана с экзотермическими химическими процессами. Примеры свечения за счёт химических реакций: свечение ночного моря, голубой свет газовой горелки, слабое белёсое свечение гнилого дерева в лесу. Многочисленны примеры хемилюминесценции в живых организмах (биолюминесценции): светящиеся бактерии, светлячки, рыбы, либо имеющие специальные светоносные органы, либо извергающие светящуюся жидкость.
Явление люминесценции характеризуется крайне высокой чувствительностью: достаточно иногда 10 -10 г светящегося вещества, например в растворе, чтобы обнаружить его по характерному свечению. Этот факт лежит в основе люминесцентного анализа, который позволяет обнаружить ничтожно малые примеси и судить о загрязнениях или процессах, приводящих к изменению исходного вещества.
Явление свечения живых организмов, связанное с протеканием в них окислительных реакций, называется
Какое превращение происходит при фосфоресценции?
1) электромагнитного излучения меньшей длины волны в энергию электромагнитного излучения большей длины волны
2) электромагнитного излучения меньшей частоты в энергию электромагнитного излучения большей частоты
3) химической реакции медленного окисления фосфора в энергию электромагнитного излучения
4) электромагнитного излучения в энергию химических соединений
Часть 2.
При выполнении задания 22 с развернутым ответом запишите сначала номер задания, а затем ответ на него. Полный ответ должен включать не только ответ на вопрос, но и его развернутое, логически связанное обоснование.
Имеются два одинаковых кристалла, обладающие свойством фосфоресцировать в жёлтой части спектра. Оба кристалла были предварительно освещены: первый — красными лучами, второй — фиолетовыми лучами. Для какого из кристаллов можно будет наблюдать послесвечение? Ответ поясните.
Образец возможного ответа
Для второго кристалла можно будет наблюдать послесвечение.
Длина волны возбуждающего света должна быть меньше длины волны света фосфоресценции. Лучи фиолетового цвета имеют меньшую длину волны по сравнению с лучами жёлтого цвета, а лучи красного цвета — большую длину волны.
При выполнении заданий 23–26 запишите сначала номер задания, а затем ответ на него.
Определите работу, совершаемую силой упругости при подъёме грузов на высоту 20 см. Используйте для этого штатив с муфтой, неподвижный блок, нить, три груза и динамометр, соберите экспериментальную установку для измерения работы силы упругости при равномерном подъёме грузов с использованием неподвижного блока.
1) сделайте рисунок экспериментальной установки;
2) запишите формулу для расчёта работы силы упругости;
3) укажите результаты прямых измерений силы упругости и пути;
4) запишите числовое значение работы силы упругости.
1) Схема экспериментальной установки:
3) Fупр = 3,0 Н; S = 0,2 м
4) А = 3,0 Н • 0,2 м = 0,6 Дж
Задание 24 представляет собой вопрос, на которых необходимо дать письменный ответ. Полный ответ должен включать не только ответ на вопрос, но и его развернутое, логически связанное обоснование.
Шарик плавает при полном погружении в воде. Изменится ли (и если изменится, то как) выталкивающая сила, действующая на шарик, если его переместить в машинное масло? Ответ поясните.
Образец возможного ответа
Выталкивающая сила уменьшится.
Выталкивающая сила, действующая на брусок в воде, уравновешивает силу тяжести. Деревянный брусок, плавающий при полном погружении в воде, утонет в машинном масле, так как плотность масла меньше плотности воды. В машинном масле выталкивающая сила будет меньше силы тяжести и, следовательно, меньше выталкивающей силы в воде.
Для заданий 25–26 необходимо написать полное решение, которое включает запись краткого условия задачи (Дано), запись формул, применение которых необходимо и достаточно для решения задачи, а также математические преобразования и расчеты, приводящие к числовому ответу.
Свинцовый шар массой m1 = 100 г, движущийся со скоростью 4 м/с, догоняет свинцовый шар массой m2 = 200 г, движущийся в том же направлении со скоростью 2 м/с. В результате соударения шары слипаются и движутся как одно целое. Какую кинетическую энергию будут иметь шары после соударения?

Прямолинейный проводник подвешен горизонтально на двух нитях в горизонтальном однородном магнитном поле с индукцией 0,05 Тл. При пропускании через проводник электрического тока натяжение вертикальных нитей уменьшилось в три раза. Чему равна сила тока? Проводник имеет длину 40 см и массу 4 г.

Здесь появится результат тестовой части.
Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы.

Сборник идеальных эссе по обществознанию
Электронная книга в формате PDF, где мы собрали 30 образцовых эссе по
5 блокам тем.
Физика 7 класс. Архимедова сила. Конспект

Действие жидкости и газа на погруженное в них тело. Архимедова сила. Плавание тел.
На тело, находящееся в жидкости, действует сила, выталкивающая это тело из жидкости. На тела, находящиеся в газе, действует сила, выталкивающая их из газа.
Сила, выталкивающая тело из жидкости или газа, направлена противоположно силе тяжести, приложенной к этому телу.
Поэтому если взвесить какое-либо тело в жидкости или газе, то его вес окажется меньше веса в вакууме. Именно этим объясняется, что в воде человек легко поднимает тела, которые с трудом удерживает в воздухе.
Сила, выталкивающая целиком погружённое в жидкость тело, равна весу жидкости в объеме этого тела.
Сила, выталкивающая тело из газа, также равна весу газа, взятого в объеме тела.
Силу, выталкивающую тело из жидкости или газа, называют архимедовой силой FA
в честь древнегреческого учёного Архимеда, который впервые указал на её существование и рассчитал её значение.

то есть, архимедова сила зависит от плотности жидкости ρ, в которую погружено тело, и от объёма V этого тела.
Если тело погружено в жидкость (или газ), то оно теряет в своем весе столько, сколько весит вытесненная им жидкость (или газ).

На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх.
1. Если сила тяжести Fтяж больше архимедовой силы FA, то тело будет опускаться на дно, тонуть:
F тяж > FA, тело тонет
2. Если сила тяжести Fтяж равна архимедовой силе FA, то тело может находиться в равновесии в любом месте жидкости:
F тяж = FA, тело плавает
3. Если сила тяжести Fтяж меньше архимедовой силы FA, то тело будет подниматься из жидкости, всплывать:
F тяж < FA, тело всплывает
Если тело плавает в жидкости, то вес вытесненной им жидкости равен весу этого тела в воздухе.
Если плотность сплошного твердого тела больше плотности жидкости, то тело в такой жидкости тонет. Тело с меньшей плотностью всплывает в этой жидкости.
Пример:
кусок железа тонет в воде, но всплывает в ртути.
Тело, плотность которого равна плотности жидкости, остаётся в равновесии внутри жидкости.

Вес воды, вытесняемой подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Глубину, на которую судно погружается в воду, называют осадкой. Наибольшая допускаемая осадка отмечена на корпусе судна красной линией, называемой ватерлинией.
Вес воды, вытесняемой судном при погружении до ватерлинии, равный силе тяжести, действующей на судно с грузом, называется водоизмещением судна.
Если из водоизмещения вычесть вес самого судна, то получим грузоподъемность этого судна. Грузоподъемность показывает вес груза, перевозимого судном.
Читайте также: