Сосуд в котором находится газ представляет из себя цилиндр переменного внутреннего диаметра
Дьюара сосуды
Сосу́д Дью́ара — сосуд, предназначенный для длительного хранения веществ при повышенной или пониженной температуре. Перед помещением в сосуд Дьюара вещество необходимо нагреть или охладить. Постоянная температура поддерживается пассивными методами, за счет хорошей теплоизоляции и/или процессов в хранимом веществе (например, кипение). В этом основное отличие сосуда Дьюара от термостатов, криостатов.
Содержание
История изобретения
Физики Кароль Ольшевский и Зыгмунт Вроблевский для хранения сжиженных газов использовали стеклянный ящик с двойными стенками, с откачанным из межстеночного пространства воздухом. Этот контейнер в 1881 году разработал немецкий физик Адольф Фердинанд Вейнхольд.
Шотландский физик и химик сэр Джеймс Дьюар в 1892 году усовершенствовал стеклянный ящик Вейнхольда, превратив его в двустенную колбу с узким горлом для уменьшения испарения жидкости. Межстеночное пространство посеребрено и из него откачан воздух. Всю эту хрупкую конструкцию Дьюар подвесил на пружинах в металлическом кожухе. Благодаря своей разработке Дьюар первым смог получить и сохранить жидкий (1898) и даже твердый (1899) водород

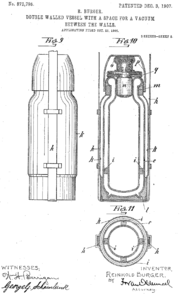
Первые сосуды Дьюара для коммерческого использования были произведены в 1904 году, когда была основана немецкая компания Термос (нем. Thermos GmbH ). Компания Thermos существует и сегодня. Она по-прежнему выпускает одни из лучших в мире термосов. Девиз компании гласит: «Храним тепло. С 1904 года». Фирмой Thermos Bottle Company 3 декабря 1907 г. был получен патент США U.S. Patent 872795 (англ.) на «Сосуд с двойными стенками и вакуумом между ними». Патент оформлен на Рейнольда Бюргера (нем. Reinhold Burger ), немецкого изобретателя и производителя стеклянных инструментов. Имя Дьюара в патенте не упоминается. В Германии Рейнольд Бюргер (нем.) считается изобретателем термоса.
Устройство
Оригинальный сосуд Дьюара представлял из себя стеклянную колбу с двойными стенками, между которыми выкачан воздух. Для уменьшения потери на излучение обе внутренние поверхности колбы были покрыты отражающим слоем. Дьюар использовал в качестве отражающего покрытия серебро. Подобная конструкция применяется и в современных дешевых бытовых термосах.
Современные конструкции

Современные сосуды Дьюара конструктивно выполнены несколько иначе. Внутренний и внешний сосуды делают из алюминия или нержавеющей стали. Теплопроводность материала не важна, а прочность и вес играют большую роль. Горловина соединяет внутренний и внешний сосуды. В дьюарах объемом до 50 л внутренний сосуд крепится только на горловине и она испытывает большие физические нагрузки. Также к ней предъявляются высокие требования по теплопроводности. Т.е. горловина должна быть прочной, но тонкой. В обычных сосудах горловину делают из нержавеющей стали. В высококачественных сосудах Дьюара горловина изготовляется из прочного армированного пластика. При этом возникает проблема вакуумноплотного крепления металла и пластика. Снаружи внутренний сосуд покрывается адсорбентом, который при охлаждении поглощает остаточные газы из вакуумной полости. Для уменьшения теплопотерь внутренний сосуд покрывают дополнительной теплоизоляцией. К крышке дьюара, для снижения конвекционной теплопередачи прикрепляют пенопластовый цилиндр, который негерметично закрывает горловину. Вакуумную полость откачивают до давления 10 -2 Па. От серебрения внутренних поверхностей отказались и заменили его полировкой.
Современные сосуды Дьюара имеют низкие потери от испарения: от 1,5 % в сутки для больших емкостей, до 5 % в сутки – для малых объёмов.
Гелиевые сосуды Дьюара

Гелий имеет очень маленькую теплоту испарения. Поэтому для снижения теплопотерь в гелиевых дьюарах применяются тепловые экраны, охлаждаемые жидким азотом. Экраны изготавливают из материалов, хорошо проводящих тепло (медь). Такой сосуд Дьюара имеет две горловины: для жидких азота и гелия. Гелиевая горловина оборудована специальными штуцерами для газосброса, подсоединения сифона, манометра, клапана. Гелиевый дьюар нельзя наклонять, он всегда должен находиться в вертикальном положении.
С развитием техники многослойной экранно-вакуумной термоизоляции на рынке появились предложения гелиевых сосудов Дьюаров в которых не используется охлаждение жидким азотом. По утверждениям производителей в таких сосудах Дьюара потери на испарение составляют 1 % в день для емкостей на 100 л.

Назначение и применение
- В быту и в пищевой индустрии сосуды Дьюара часто применяются для сохранения температуры еды или напитков (термосы).
- В лабораториях и в промышленности сосуд Дьюара используется для хранения криожидкостей, чаще всего жидкого азота.
- В медицине и ветеринарии специальные сосуды Дьюара используются для длительного хранения биологических материалов при низких температурах.
Источники
- Burger, R., U.S. Patent 872795 (англ.) , «Double walled vessel with a space for a vacuum between the walls», December 3, 1907.
- Сивухин Д. В. Общий курс физики. — М .: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.
См. также
Ссылки
Wikimedia Foundation . 2010 .
Смотреть что такое "Дьюара сосуды" в других словарях:
Дьюара сосуды — (по имени Дж. Дьюара) сосуды с двойными стенками, между которыми создан вакуум [не менее 1,33 мн/м2 (10 5 мм рт. cт.)], что обеспечивает высокую теплоизоляцию вещества, находящегося внутри сосуда. Теплообмен в Д. с. происходит практически … Большая советская энциклопедия
Дьюара сосуд — колба с двойными посеребрёнными изнутри стенками, из пространства между которыми выкачан воздух. Теплопроводность разрежённого газа между стенками столь мала, что температура веществ, помещаемых в Дьюара сосуд, сохраняется постоянной долгое время … Энциклопедический словарь
ДЬЮАРА СОСУД — колба с двойными посеребренными изнутри стенками, из пространства между которыми выкачан воздух. Теплопроводность разреженного газа между стенками столь мала, что температура веществ, помещаемых в сосуд Дьюара, сохраняется постоянной долгое время … Большой Энциклопедический словарь
СОСУД ДЬЮАРА — Специальный холодильный сосуд для замораживания и хранения спермы производителей в жидком азоте. Представляет собой двухстенную емкость из алюминиевых сплавов или нержавеющей стали. Между стенками помещена специальная теплоизоляция. Для повышения … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных
Что такое гидравлические цилиндры? Их виды и типы

Гидравлические цилиндры являются важным компонентом в области гидравлики, специальной формы передачи энергии, которая использует энергию, передаваемую при перемещении жидкостей под давлением, и преобразует ее в механическую энергию.
Передача энергии, как общий термин, относится к процессу использования технологий для преобразования энергии в практические, пригодные для использования формы. В категории передачи энергии гидравлика попадает в подкатегорию гидравлической энергии, которая зависит от движущихся текучих сред (как газов, так и жидкостей) для производства энергии.
История гидравлического привода и цилиндров
История гидроцилиндров неразрывно связана с историей гидроэнергетики в целом. С технической точки зрения, гидравлику можно отнести к древним временам, когда сила движущейся воды использовалась для различных целей. Основным применением гидравлики было использование движущейся воды для перемещения колес. Древний Рим использовал такую гидравлику для работы мельниц, производящих самые разные продукты (например, муку, древесину и т. д.).
История современной гидравлики восходит к 1648 году, когда французский ученый Блез Паскаль обнаружил, что давление в замкнутой жидкости должно оставаться постоянным и действует одинаково во всех направлениях. Однако этот теоретический принцип (известный как «Закон Паскаля» или «Принцип Паскаля») не нашел практического применения до следующего столетия.

В 1738 году Даниэль Бернулли опирался на работу Паскаля, описывая поведение жидкости при различных условиях потока и высоты (принцип Бернулли) и используя свои идеи для работы с насосами и мельницами. В 1795 году англичанин Джозеф Брама запатентовал первую практичную гидравлическую машину: пресс с гидравлическим приводом.
Почти полвека спустя (1840 г.) Уильям Армстронг разработал более эффективные применения гидравлической энергии, чем водяные мельницы, в том числе кран с гидравлическим приводом. Вместе,
Цилиндры сыграли фундаментальную роль в творчестве Брамы и Армстронга. Практический прорыв Брамы произошел, когда он обнаружил, как приводить в действие движущуюся пластину своего пресса через поток жидкости между меньшим и большим цилиндрами.
Детали гидроцилиндров
Гидравлический цилиндр содержит некоторые из наиболее важных механических компонентов гидравлической системы. Несмотря на их впечатляющую роль в преобразовании кинетической энергии в механическую, основные гидроцилиндры являются относительно простыми устройствами. Основные компоненты гидроцилиндров включены в следующий список:
- Круглый, прямоугольный или овальный цилиндр в форме трубы составляет основной корпус цилиндра, в котором находятся и соединяются все компоненты.
- На одном конце этого цилиндра находится крышка цилиндра, которая закрывает неподвижный конец цилиндра. Головка блока цилиндров закрывает другой конец, но имеет круглое уплотнение, через которое шток поршня может входить и выходить. (Цилиндры двустороннего действия имеют головку блока цилиндров на обоих концах и не имеют торцевой крышки.)

- Поверхность поршня представляет собой металлическую дискообразную деталь, которая точно соответствует поперечному сечению цилиндра цилиндра, разделяя камеру на два меньших отсека. Поршень необходим для создания линейного движения за счет повышения давления гидравлической жидкости. В цилиндрах любого типа корпуса используются гидравлические поршни (например, те, которые предлагаются поставщиками, перечисленными в Справочнике IQS) для подъема, поворота, наклона, сжатия, поворота, тяги и толкания тяжелых компонентов машин и любых прикрепленных грузов. Эта напряженная работа требует, чтобы они были изготовлены из прочных материалов.
- К поршню прикреплен шток поршня. Шток частично размещен внутри ствола, но выходит за пределы корпуса через головку цилиндра и прикреплен к компонентам машины, которые должны перемещаться с помощью различных монтажных приспособлений.
- Каждый отсек внутри цилиндра также имеет порт, через который вводится гидравлическая жидкость под высоким давлением и через которую жидкость без давления возвращается в резервуар.
- Несколько уплотнений размещены вокруг головки поршня, клапанов потока и головки цилиндров, чтобы гарантировать, что жидкости не просачиваются в, из или из одного отсека в другой, вызывая потерю давления и снижение функциональности.
Типы гидроцилиндров
- Гидравлические цилиндры двойного действия используют гидравлическое давление для приведения в действие штока, чтобы он выдвигался и втягивался в обоих направлениях.
- Гидравлические цилиндры для тяжелых условий эксплуатации предназначены для работы в условиях высокого давления, большого расхода и тяжелых условий эксплуатации. Цилиндры для тяжелых условий эксплуатации особенно подходят для сложных промышленных и мобильных приложений.
- Гидравлические цилиндры высокого давления имеют значительно меньшие размеры и легче, чем стандартные цилиндры, что позволяет значительно сэкономить вес и место в оборудовании. Гидравлические цилиндры высокого давления используются в приложениях, требующих больших усилий и коротких или средних ходов, таких как испытания материалов и преобразование материалов.

Как работает гидравлическая энергия?
Суть гидравлики заключается в том, что жидкости несжимаемы (в отличие от газов). Благодаря этому факту и принципу Паскаля сила, приложенная в одной точке замкнутой жидкости, может эффективно передаваться в другую точку этой жидкости и использоваться для приведения в действие различных механизмов.
Как работают гидроцилиндры?
«Закон Паскаля» применим к замкнутым жидкостям. Таким образом, чтобы жидкость действовала гидравлически, она должна работать с замкнутой системой определенного типа.
Закрытая механическая система, в которой гидравлически используется жидкость, известна как гидравлический силовой агрегат или гидравлический силовой агрегат. Эти блоки состоят из резервуара (для хранения неиспользованной гидравлической жидкости), насоса (для подачи жидкости в остальную часть гидравлической системы), различных типов трубок (для транспортировки гидравлической жидкости) и приводов (устройств). которые фактически преобразуют энергию, производимую потоком гидравлической жидкости, в механическую энергию.)
Хотя гидравлический силовой агрегат в целом спроектирован так, чтобы использовать энергию передачи жидкости, цилиндры представляют собой часть агрегата, в которой действительно происходит преобразование энергии. Внутри цилиндра (или цилиндров, которых иногда бывает несколько) есть зубчатая передача и два клапана рядом с поршнем.
В гидравлической системе для хранения и транспортировки жидкости необходимы трубки и сосуд под давлением (или гидравлический насос). Когда гидравлическая жидкость под давлением вводится в сосуд, он давит на поршень и входит в зацепление с прикрепленным к нему штоком.
Когда насос работает, поршень втянут. Это создает вакуум, который всасывает гидравлическую жидкость из резервуара через шланг и впускной клапан и, наконец, в цилиндр. Когда поршень возвращается в исходное положение и обратный клапан закрывается, жидкость находится под давлением.

Это перекачивающее действие повторяется с переменной скоростью до тех пор, пока в цилиндре не будет создано достаточное давление, чтобы заставить жидкость пройти через выпускной клапан. Это создает энергию, необходимую для работы навесного оборудования и перемещения предполагаемого груза.
Направление определяется тем, с какой стороны поршень встречается с жидкостью под давлением. Жидкость над поршнем втягивает шток, а жидкость под ним заставляет его расширяться. Введение различных количеств гидравлической жидкости под давлением с обоих концов управляет движением поршня, штока и прикрепленной нагрузки.
Применение гидроцилиндров
Гидравлические системы и их использование широко используются в самых разных областях, включая строительные, сельскохозяйственные, промышленные, транспортные (например, автомобильную, аэрокосмическую), различные морские рабочие среды и т. д.
Лифты, погрузочно-разгрузочное оборудование, снегоочистители, тормоза, мощность рулевое управление, экскаваторы, бульдозеры, экскаваторы, краны , лифты, вилочные погрузчики, домкраты, самосвалы, космические корабли, корабли, самолеты и даже современные роботизированные манипуляторы используют силу гидравлики.
Гидравлические цилиндры чрезвычайно разнообразны, что позволяет использовать их в различных отраслях промышленности.

По мере того как отрасли продолжают расти, растут и требуемые возможности гидроцилиндров, промышленного оборудования и машин, частью которых они являются.
Уход за гидроцилиндрами
Несмотря на то, что гидравлические системы проще по сравнению с электрическими или механическими системами, они по-прежнему являются сложными системами, с которыми следует обращаться только осторожно. Для гидроцилиндров особенно важно, чтобы они применялись по назначению, например, для операций линейного толкания или тяги.
Вообще говоря, неразумно широко использовать гидроцилиндры в ситуациях, связанных с изгибающими движениями и боковым давлением. Даже при оснащении соответствующими аксессуарами, которые обеспечивают не только линейное движение (например, вилка), передовой опыт включает использование гидравлического цилиндра для нелинейного движения только в отдельных случаях.

Ранее подчеркивалось, что гидроцилиндры должны быть изготовлены из прочных материалов из-за больших нагрузок, которым они подвергаются. Однако даже такие цилиндры, как гидроцилиндры из нержавеющей стали, со временем могут подвергнуться коррозии или выйти из строя.
Особенности производства гидравлических цилиндров
Хотя гидравлическая передача энергии чрезвычайно полезна в широком спектре профессионального использования, обычно никогда не стоит полагаться на одну форму передачи энергии.
Каждый тип передачи энергии (электрический, механический и гидравлический) лучше всего работает, когда он интегрирован в общую стратегию передачи энергии.
Что касается гидроцилиндров, важно отметить, что все компоненты цилиндров должны быть изготовлены из прочных материалов, которые могут выдерживать трение и тепло, создаваемые при использовании гидроцилиндра.
- Процессы штамповки или экструзии используются для производства уплотнений из нитрильного каучука, витона, полипропилена, латуни или нержавеющей стали в зависимости от области применения.
- Поршни изготавливаются из латуни, стали, нержавеющей стали, алюминия, чугуна или бронзы.
- Поршневые штоки и цилиндры изготавливаются из одних и тех же материалов, но производятся с помощью разных производственных процессов. Холодная прокатка используется для изготовления стержней, которые часто имеют твердое хромирование для защиты от коррозии и износа.
- Внутренняя поверхность ствола должна иметь микро гладкую поверхность, позволяющую поршню чисто перемещаться по корпусу с минимальными потерями энергии на трение.
Вышеупомянутые компоненты также должны быть совместимы с гидравлической жидкостью, которая обычно представляет собой композиционный материал на основе минералов, масел, эфира или воды. Однако выбор подходящего гидроцилиндра для конкретного применения требует не только технологии производства, материала корпуса и жидкости.
Дополнительные соображения включают, среди прочего, максимальное рабочее давление, ход, размер отверстия и диаметр штока. Поскольку рабочая сила, создаваемая гидравликой под давлением, может значительно различаться, важно понимать системные требования, прежде чем выбирать конкретную модель.
Как снизить затраты на ремонт и замену гидроцилиндров
Гидравлические цилиндры, как и обычные воздушные цилиндры, являются источником энергии для большого количества насосов и двигателей. Если ваше промышленное оборудование работает на гидравлическом оборудовании, то вы можете понять, насколько проблематичными могут стать затраты на их ремонт и обслуживание.

Кроме того, источник энергии, например, гидроцилиндр, также следует выбирать в соответствии с техническими характеристиками устройства.
Чтобы держать под контролем затраты на ремонт и замену машин, необходимо выполнять работы по техническому обслуживанию в соответствии с графиком и по мере необходимости.
Сосуд в котором находится газ представляет из себя цилиндр переменного внутреннего диаметра
Рассмотрим различные случаи истечения жидкости из резервуаров, баков, котлов через отверстия и насадки (коротки трубки различной формы) в атмосферу или пространство, заполненное газом или той же жидкость. В процессе такого истечения запас потенциальной энергии, которым обладает жидкость, находящаяся в резервуаре, превращается в кинетическую энергию свободной струи.
Основным вопросом, который интересует в данном случае, является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.
Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рис.5.1).
Степень сжатия оценивается коэффициентом сжатия.
где Sс и Sо - площади поперечного сечения струи и отверстия соответственно; dс и dо - диаметры струи и отверстия соответственно.
Скорость истечения жидкости через отверстие такое отверстие
где Н - напор жидкости, определяется как
φ- коэффициент скорости
где α - коэффициент Кориолиса;
ζ- коэффициент сопротивления отверстия.
Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:
Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ.
В итоге получаем расход
где ΔР - расчетная разность давлений, под действием которой происходит истечение.
При помощи этого выражения решается основная задача - определяется расход.
Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям. На рис.5.3 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости
| Рис. 5.3. Зависимость ε, φ и от числа Reu | Рис. 5.4. Инверсия струй |
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи (рис.5.4). Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых стенок резервуара (рис.5.5).
Так как боковые стенки частично направляют движение жидкости при подходе к отверстию, то струя по выходе из отверстия сжимается в меньшей степени, чем из резервуара неограниченных размеров, как это было описано в п.5.1.
При истечении жидкостей из цилиндрического резервуара круглого сечения через круглое отверстие, расположенное в центре торцевой стенки, при больших числах Re коэффициент сжатия для идеальной жидкости можно найти по формуле, представленной Н.Е. Жуковским:
где n - отношение площади отверстия Sо к площади поперечного сечения резервуара S1
Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же жидкостью (рис.5.6). такой случай называется истечением под уровень, или истечением через затопленное отверстие.
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Скорость истечения в сжатом сечении струи
где φ - коэффициент скорости;
Н - расчетный напор,
Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость и расход жидкости в данном случае не зависят от высот расположения отверстия.
Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без закругления входной кромки (рис. 5.7). На практике такой насадок часто получается в тех случаях, когда выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в газовую среду может происходить в двух режимах.
Первый режим - безотрывный режим. При истечении струя, после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров отверстия из насадка выходит полным сечением (рис.5.7).
Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа Рейнольдса, определяется по эмпирической формуле:
Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.
Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадком 2-2 и преобразовать его, то можно получить падение давления внутри насадка
При некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение 1-1) становится равным нулю (P1 = 0), и поэтому
Следовательно, при Н > Нкр давление P1 должно было бы стать отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится невозможным. Поэтому при Н Нкр происходит изменение режима истечения, переход от первого режима ко второму (рис.5.8).
Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же, как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.
При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается кавитационный режим.
Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме - большое сопротивление и недостаточно высокий коэффициент расхода, а на втором - очень низкий коэффициент расхода. Недостатком также является возможность кавитации при истечении под уровень.
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или устройства конического входа. На рис.5.9 даны различные типы насадков и указаны значения соответствующих коэффициентов.
Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.). Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся (рис.5.10).
Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровнеS, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:
где dh - изменение уровня жидкости за время dt.
Отсюда время полного опорожнения сосуда высотой Н
Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного опорожнения
Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.
| Рис. 5.11. Опорожнение призматического резервуара | Рис. 5.12. Опорожнение непризматического резервуара |
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 5.12) выразим зависимость переменной площади S от h:
где l - длина цистерны; D - диаметр цистерны.
Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным
Во многих водозаборных и водопропускных гидротехнических сооружениях расходы воды проходят через отверстия, перекрываемые затворами. Затворы поднимают на определенную высоту над дном и пропускают через отверстия необходимые расходы. Чаще всего на гидромелиоративных сооружениях устраивают отверстия прямоугольного сечения, истечение из которых и рассмотрим.
Отверстия могут быть незатопленными (истечение свободное) и затопленными, когда уровень воды за затвором влияет на истечение.
Если отверстие незатопленное, то вытекающая из-под затвора струя находится под атмосферным давлением (рис. 5.13). При истечении через затопленное отверстие струя за затвором находится под некоторым слоем воды (рис. 5.14).
Когда затвор приподнят над дном, вытекающая из-под него струя испытывает сжатие в вертикальной плоскости. На расстоянии, примерно равном высоте отверстия а (высоте поднятия затвора), наблюдается наиболее сжатое сечение. Глубина в сжатом сечении hc связана с высотой отверстия а следующей зависимостью:
где ε' - коэффициент вертикального сжатия струи.
Коэффициент вертикального сжатия ε' зависит от отношения высоты отверстия а к напору (глубине воды перед затвором) Н. Для ориентировочных расчетов можно принимать ε' = 0,64.
Если составить уравнение Бернулли для сечений, проведенных перед затвором и в сжатом сечении, после преобразований получим:
Глубина hz определяется из зависимости
а hб - глубина в отводящем канале (бытовая глубина).
Если вытекающая из отверстия или насадка струя попадает на неподвижную стенку, то она с определенным давлением воздействует на нее. Основное уравнение, по которому вычисляется давление струи на площадку, имеет вид
На рис. 5.15 приведены наиболее часто встречающиеся в практике ограждающие поверхности (преграды) и уравнения, по которым вычисляется давление струи на соответствующую поверхность.
Величина давления струи, естественно, зависит от расстояния насадка до преграды. С увеличением расстояния струя рассеивается и давление уменьшается. Соответствующие исследования показывают, что в данном случае струя может быть разбита на три характерные части: компактную, раздробленную и распыленную (рис.5.16).
В пределах компактной части сохраняется цилиндрическая форма струи без нарушения сплошности движения. В пределах раздробленной части сплошность потока нарушается, причем струя постепенно расширяется. Наконец, в пределах распыленной части струи происходит окончательный распад потока на отдельные капли.
Элементы механики жидкостей и газов
где h – высота столба жидкости.
· Закон Паскаля: давление в любом месте покоящейся жидкости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому покоящейся жидкостью (рис. 8)
Рис. 8. Принцип действия гидравлического пресса
· Коэффициент динамической вязкости жидкости
где R – радиус капилляра длиной l; V – объем вытекаемой жидкости; t – время истечения жидкости.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1.В два колена U-образной трубки налиты вода и масло, разделенные ртутью. Поверхности раздела ртути и жидкостей в обоих коленах находятся на одной высоте. Определить высоту столба воды, если высота столба масла 20 см. Плотность воды 1000 кг/м 3 , плотность масла 900 кг/м 3 .
Решение: Согласно закону Паскаля давление в обоих коленах трубки одинаково
Пример 2.Однородное тело плавает на поверхности керосина так, что объем погруженной части составляет 0,92 всего объема тела. Определите объем погруженной части при плавании тела на поверхности воды.
Решение: Обозначим через V объем всего тела, Vп – объем погруженной части тела, плавающего в керосине, V'п – объем погруженной части тела, плавающего в воде.
На тело, плавающее в керосине, действуют сила тяжести , выталкивающая сила керосина . Из условия плавания следует, что или
Аналогично запишем условие плавания тела в воде
Из уравнений (1) и (2) получим
Решение: Разность сил найдем, отняв от силы давления F2 воды на стенку силу давления F1 на дно цилиндра: , где и . Здесь р1 – давление воды на дно цилиндра, – площадь дна, р2 – давление воды на стенку и – площадь стенки цилиндра. Поскольку и согласно условию D = H,
Давление воды на дно р1 определим через плотность и высоту: .
Решение: Определим вначале, какую силу F2 развил бы большой поршень, если бы в узлах механизма отсутствовало трение и иные помехи, т.е. если бы КПД был равен 100 %. Согласно формуле гидравлического пресса:
Здесь F1 – сила, прилагаемая коротким плечом рычага к малому поршню. Эту силу определим, воспользовавшись правило м рычага: рычаг дает выигрыш в силе во столько раз, во сколько его длинное плечо длиннее короткого:
Подставим (2) в (1): .
Рис. 9. Схема гидравлического пресса
Такое усилие развил бы пресс, если бы его КПД был равен 100 %. Но из-за различных помех оно станет меньше и будет:
При равномерном подъеме груза сила тяжести , приложенная к нему, будет уравновешена силой F0, поэтому или ,
Тепловое расширение. Газовые законы
В два сосуда конической формы, расширяющихся кверху и книзу, и цилиндрический налита вода при температуре T = 100 °C. Как изменится давление на дно сосудов после охлаждения воды до комнатной температуры?
В сосуде конической формы, расширяющемся кверху, давление на дно увеличится. В сосуде конической формы, расширяющемся книзу, давление на дно уменьшится. В цилиндрическом сосуде давление на дно не изменится.
Две линейки — одна медная, другая железная — наложены одна на другую так, что они совпадают только одним концом. Определить длины линеек при t = 0 °C, зная, что разность их длин при любой температуре составляет Δl = 10 см. Коэффициент линейного расширения меди α1 = 17·10 -6 К -1 , железа — α2 = 12·10 -6 К -1 .
Длина медной линейки 24 см, длина железной — 34 см.
Часы, маятник которых состоит из груза малых размеров и легкой латунной нити, идут правильно при 0 °C. Найти коэффициент линейного расширения латуни, если при повышении температуры до t = +20 °C часы отстанут за сутки на 16 с.
На сколько часы будут уходить вперед за сутки при t0 = 0 °C. если они выверены при t = 20 °C, и материал, из которого сделан маятник, имеет коэффициент линейного расширения α = 0,000012 К -1 ?
При t0 = 0 °С часы спешат в сутки на τ = 20 с. При какой температуре часы будут идти точно? Коэффициент линейного расширения материала маятника α = 1,9·10 -5 К -1 .
Какую силу F надо приложить к стальному стержню сечением S = 1 см 2 , чтобы растянуть его на столько же, на сколько он удлиняется при нагревании на Δt = 1 °С? Коэффициент линейного расширения α = 12·10 -6 К -1 . Модуль Юнга E = 2,1·10 11 Н/м 2 .
Толщина биметаллической пластинки, составленной из одинаковых полосок стали и цинка, равна d = 0,1 см. Определить радиус кривизны r пластинки при повышении температуры на Δt = 11 °С. Коэффициент линейного расширения цинка α1= 25·10 -6 К -1 , а стали α2 = 12·10 -6 К -1 .
Концы стального стержня сечением S = 1 см 2 , находящегося при температуре t = 20 °С, прочно закреплены. С какой силой стержень будет действовать на опоры, если его нагреть до t1 = 200 °С? Модуль Юнга стали E = 2,0·10 11 Н/м 2 , коэффициент линейного расширения α =1,2·10 -5 К -1 ?
F = 39600 Н.
Каково давление газа p0 в электрической лампочке, объем которой V = 1 л, если при отламывании кончика последней под поверхностью воды на глубине h = 1 м в лампочку вошло m = 998,7 г воды? Атмосферное давление нормальное.
Стеклянный баллон объемом V = 1 л был наполнен испытуемым газом до давления p = 10 5 Па и взвешен. Его вес оказался равным Q = 0,9898 Н. Затем часть газа была удалена так, что давление в баллоне упало до р1 = 5·10 4 Па. Новый вес баллона оказался равным Q1 = 0,9800 Н. Какова плотность испытуемого газа при нормальном атмосферном давлении? Температура постоянна.
ρ = 2,1 кг/м 3 .
p1 = 751 мм рт. ст.
Открытую стеклянную трубку длиной l = 1 м наполовину погружают в ртуть. Затем трубку закрывают пальцем и вынимают. Какой длины столбик ртути останется в трубке? Атмосферное давление равно H = 750 мм рт. ст.
В запаянной с одного конца стеклянной трубке длиной l = 90 см находится столбик воздуха, запертый сверху столбиком ртути высотой h = 30 см; столбик ртути доходит до верхнего края трубки. Трубку осторожно переворачивают открытым концом вниз, причем часть ртути выливается. Какова высота столбика ртути, которая останется в трубке, если атмосферное давление H = 750 мм рт. ст.?
В сосуд со ртутью опускают открытую стеклянную трубку, оставляя над поверхностью конец длиной l = 60 см. Затем трубку закрывают и погружают еще на 30 см. Определить высоту столба воздуха в трубке. Атмосферное давление p0 = 760 мм рт. ст.
.
Посередине откачанной и запаянной с обоих концов горизонтальной трубки длиной L = 1 м находится столбик ртути длиной h = 20 см. Если трубку поставить вертикально, столбик ртути сместится на l = 10 см. До какого давления была откачана трубка? Плотность ртути ρ = 1,36·10 4 кг/м.
Расположенная горизонтально запаянная с обоих концов стеклянная трубка разделена столбиком ртути, на две равные части. Длина каждого столбика воздуха 20 см. Давление 750 мм рт. ст. Если трубку повернуть вертикально, ртутный столбик опускается на 2 см. Определить длину столбика ртути.
Цилиндрический сосуд делится на две части тонким подвижным поршнем. Каково будет равновесное положение поршня, когда в одну часть сосуда помещено некоторое количество кислорода, в другую — такое же по массе количество водорода, если длина сосуда l = 85 см?
В закрытом цилиндрическом сосуде с площадью основания S находится газ, разделенный поршнем массой M на два равных отсека. Масса газа под поршнем при этом в k раз больше массы газа над ним. Температуры газов одинаковы. Пренебрегая трением и массой газа по сравнению с массой поршня, найти давление газа в каждом отсеке.
; .
Имеются два мяча различных радиусов, давление воздуха в которых одинаково. Мячи прижимают друг к другу. Какой формы будет поверхность соприкосновения?
Выгнута в сторону мяча с большим радиусом.
Найти число n ходов поршня, которое надо сделать, чтобы поршневым воздушным насосом откачать воздух из сосуда емкостью V от давления p0 до давления p, если емкость насоса ΔV.
.
Упругость воздуха в сосуде равна 97 кПа. После трех ходов откачивающего поршневого насоса упругость воздуха упала до 28,7 кПа. Определить отношение объемов сосуда и цилиндра насоса.
Два баллона соединены трубкой с краном. В первом находится газ при давлении p = 10 5 Па, во втором — при p1 = 0,6·10 5 Па. Емкость первого баллона V1 = 1 л, второго — V2 = 3 л. Какое давление установится в баллонах (в мм рт. ст.), если открыть кран? Температура постоянная. Объемом трубки можно пренебречь.
Три баллона емкостями V1 = 3 л, V2 = 7 л и V3 = 5 л наполнены соответственно кислородом (p1 = 2·10 5 Па), азотом (p2 = 3·10 5 Па) и углекислым газом (p3 = 6·10 4 Па), при одной и той же температуре. Баллоны соединяют между собой, причем образуется смесь той же температуры. Каково давление смеси?
На гладком горизонтальном столе находится сосуд, разделенный перегородкой на две равные части. В одной части сосуда находится кислород, а в другой — азот. Давление азота вдвое больше давления кислорода. На сколько сдвинется сосуд, если перегородка станет проницаемой? Длина сосуда l = 20 см. Массой сосуда пренебречь. Процесс считать изотермическим.
В цилиндре, закрытом легко подвижным поршнем массой m и площадью S, находится газ. Объем газа равен V. Каким станет объем газа, если цилиндр передвигать вертикально с ускорением: а) +a; б) -a? Атмосферное давление равно p0, температура газа постоянна.
а) ; б) .
Начертить графики изотермического, изобарического и изохорического процессов в идеальном газе в координатах p, V; p, T; V, T. Объяснить, почему коэффициент объемного расширения идеальных газов равен термическому коэффициенту давления.
На рисунке изображены две изотермы одной и той же массы газа.

1. Чем отличаются состояния газов, если газы одинаковы?
2. Чем отличаются газы, если температуры газов одинаковы?
Как менялась температура идеального газа — увеличивалась или уменьшалась — при процессе, график которого в координатах p, V изображен на рисунке.

При нагревании газа получен график зависимости давления от абсолютной температуры в виде прямой, продолжение которой пересекает ось p в некоторой точке выше (ниже) начала координат. Определить, сжимался или расширялся газ во время нагревания.
На рисунке дан график изменения состояния идеального газа в координатах p, V.

Представить этот круговой процесс (цикл) в координатах p, T и V, T, обозначив соответствующие точки.
Сколько ртути войдет в стеклянный баллончик объемом 5 см 3 , нагретый до t1 = 400 °С, при его остывании до t2 = 16 °С, если плотность ртути при t = 16 °С равна ρ = 13,6 г/см 3 ?

При какой температуре находился газ, если при нагревании его на Δt = 22 °С при постоянном давлении объем удвоился? Для каких газов это возможно?
До какой температуры нужно нагреть воздух, взятый при t = 20 °С, чтобы его объем удвоился, если давление останется постоянным?
Определить, каким был бы коэффициент объемного расширения идеального газа, если бы за начальный объем его принимали объем не при t0 =0°С, а при t1 = 100 °С?
В цилиндре, площадь основания которого равна S = 100 см 2 , находится воздух при температуре t1 = 12 °С. Атмосферное давление p1 = 101 кПа. На высоте h1 = 60 см от основания цилиндра расположен поршень. На сколько опустится поршень, если на него поставить гирю массой m = 100 кг, а воздух в цилиндре при этом нагреть до t2 = 27 °С? Трение поршня о стенки цилиндра и вес самого поршня не учитывать.
Два одинаковых баллона, содержащие газ при t = 0 °С, соединены узкой горизонтальной трубкой диаметром d = 5 мм, посередине которой находится капелька ртути.

Капелька делит весь сосуд на два объема по V = 200 см 3 . На какое расстояние x переместится капелька, если один баллон нагреть на Δt = 2 °С, а другой на столько же охладить? Изменением объемов сосудов пренебречь.
Два одинаковых сосуда соединены трубкой, объемом которой можно пренебречь. Система наполнена газом и находится при абсолютной температуре T. Во сколько раз изменится давление в такой системе, если один из сосудов нагреть до абсолютной температуры T1, а другой поддерживать при прежней температуре T?
1. В горизонтально расположенном сосуде, разделенном легко подвижным поршнем, находятся с одной стороны от поршня m1 граммов кислорода, а с другой — m2 граммов водорода. Температуры газов одинаковы и равны T0. Каким будет отношение объемов, занимаемых газами, если температура водорода останется равной T0, а кислород нагреется до температуры T1?
2. Вертикально расположенный сосуд разделен на две равные части тяжелым теплонепроницаемым поршнем, который может скользить без трения. В верхней половине сосуда находится водород при температуре T и давлении p. В нижней части — кислород при температуре 2T. Сосуд перевернули. Чтобы поршень по-прежнему делил сосуд на две равные части, пришлось охладить кислород до температуры T/2. Температура водорода осталась прежней. Определить давление кислорода в первом и втором случаях.
На некоторой высоте давление воздуха p = 3·10 4 Па, а температура t = -43 0 С. Какова плотность воздуха на этой высоте?
Определить давление кислорода, масса которого m = 4 кг, заключенного в сосуд емкостью V = 2 м 3 , при температуре t = 29 °С.
Определить удельный объем азота при температуре 27 °С и давлении p = 4,9·10 4 Па.
Определить массу кислорода, заключенного в баллоне емкостью V = 10 л, если при температуре t = 13 °С манометр на баллоне показывает давление p = 9·10 6 Па.
Какова разница в массе воздуха, заполняющего помещение объемом V = 50 м 3 , зимой и летом, если летом температура помещения достигает t1 = 40 °С, а зимой падает до t2 = 0 °С? Давление нормальное.
Сколько молекул воздуха выходит из комнаты объемом V0 = 120 м 3 при повышении температуры от t1 = 15 °С до t2 = 25 °С? Атмосферное давление p0 = 10 5 Па.
Компрессор захватывает при каждом качании V0 = 4 л воздуха при атмосферном давлении p = 10 5 Па и температуре t0 = -3 °С и нагнетает его в резервуар емкостью V = 1,5 м 3 , причем температура воздуха в резервуаре держится около t1 = 45 °С. Сколько качаний должен сделать компрессор, чтобы давление в резервуаре увеличилось на Δp = 1,96·10 5 Па?
На весах установлены два одинаковых сосуда. Один заполнен сухим воздухом, другой — влажным (насыщенный водяными парами) при одинаковых давлениях и температурах. Какой из сосудов тяжелее?
По газопроводу течет углекислый газ при давлении p = 5·10 5 Па и температуре t = 17 °С. Какова скорость движения газа в трубе, если за τ = 5 мин через площадь поперечного сечения трубы S = 6 см 2 протекает m = 2,5 кг углекислого газа?
Из баллона со сжатым водородом емкостью V = 10 л вследствие неисправности вентиля утекает газ. При температуре t1 = 7 °С манометр показывал p = 5·10 6 Па. Через некоторое время при температуре t2 = 17 °С манометр показал такое же давление. Сколько утекло газа?
Какая часть газа осталась в баллоне, давление в котором было равно p = 1,2·10 7 Па, а температура t = 27 °С, если давление упало до p1 = 10 5 Па? Баллон при этом охладился до t1 = -23 °С.
До какой температуры нужно нагреть запаянный шар, содержащий m = 17,5 г воды, чтобы шар разорвался, если известно, что стенки шара выдерживают давление 10 7 Па, а объем шара V = 1 л?
В цилиндре объемом V, заполненном газом, имеется предохранительный клапан в виде маленького цилиндрика с поршнем. Поршень упирается в дно цилиндра через пружину жесткости k.

При температуре T1 поршень находится на расстоянии l от отверстия, через которое газ выпускается в атмосферу. До какой температуры T2 должен нагреться газ в цилиндре, для того чтобы клапан выпустил часть газа в атмосферу? Площадь поршня S, масса газа в цилиндре m, его молярная масса µ. Объем цилиндрика клапана пренебрежимо мал по сравнению с объемом цилиндра.
В баллоне емкостью V = 110 л помещено m1 = 0,8 кг водорода и m2 = 1,6 кг кислорода. Определить давление смеси на стенки сосуда. Температура окружающей среды t = 27 °С.
В сосуде объемом 1 л заключено m = 0,28 г азота. Азот нагрет до температуры T = 1500 °С. При этой температуре α = 30% молекул азота диссоциировано на атомы. Определить давление в сосуде.
В сосуде находится смесь азота и водорода. При температуре T, когда азот полностью диссоциирован на атомы, давление равно p (диссоциацией водорода можно пренебречь). При температуре 2T, когда оба газа полностью диссоциированы, давление в сосуде 3p. Каково отношение масс азота и водорода в смеси?
Оболочка аэростата объемом V = 1600 м 3 , находящегося на поверхности Земли, наполнена водородом на n = 7/8 при давлении p = 101 кПа и температуре t = 15 °С. Аэростат поднялся на некоторую высоту, где давление p1 = 79,3 кПа и температура t1 = 2 °С. Сколько водорода потерял аэростат при своем подъеме в результате расширения газа?
Доказать, что в атмосфере с постоянной температурой независимо от закона изменения давления с высотой подъемная сила воздушного шара с эластичной оболочкой постоянна. Газ из воздушного шара не вытекает. Пренебречь давлением, обусловленным кривизной оболочки.
Читайте также: