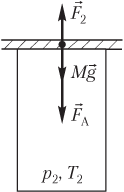При расширении газа в цилиндре с поршнем молекулы газа ударяясь об отступающий поршень
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Очевидно, что импульсы протона и p- мезона равны по величине и противоположно направлены, т. е.
Отсюда можно найти кинетическую энергию p-мезона. Для этого нужно решить квадратное уравнение относительно неизвестной кинетической энергии p-мезона
Решая его, получим = 32 МэВ. Тогда масса распавшейся частицы находится из закона сохранения энергии
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Вариант 1
1. При какой температуре средняя квадратичная скорость молекул водорода больше наиболее вероятной скорости на 100 м/с?
Средняя квадратичная скорость
Наиболее вероятная скорость
2. При расширении газа в цилиндре с поршнем молекулы газа, ударяясь об удаляющийся поршень, отражаются с меньшими скоростями, отдавая поршню часть своей энергии. Приток теплоты компенсирует это уменьшение энергии и увеличивает энергию молекул пропорционально объему. Какой это процесс?
При отскакивании от удаляющегося поршня скорость молекулы уменьшается, ибо молекула совершает работу, толкая отходящий поршень. Поэтому расширение газа, связанное с отодвиганием поршня или слоев окружающего газа, сопровождается совершением работы и приводит к уменьшению внутренней энергии газа, которую компенсируют пропорционально объему.
В связи с этим мы можем сказать, что не изохорный и адиабатический процессы. Так как внутренняя энергия:
Тогда внутренняя энергия сохраняется. Тем самым - это изотермический процесс.
Ответ: процесс изотермический
3. Кислород массой m = 250 г, имеющий температуру Т1 = 200 К, был адиабатически сжат. При этом была совершена работа А = 25 кДж. Определить конечную температуру Т2 газа.
Работу при адиабатном сжатии можно определить по формуле:
– молярная масса молекулы кислорода, .
– универсальная газовая постоянная.
Теплоёмкость при постоянном объёме определяется по формуле:
степень свободы кислород, двухатомный газ.
Выразим конечную температуру:
4. Сравнить КПД циклов 123 и 134, изображенных на рисунке. Отношение Р2/ Р1 = 2, V2/ V1 = 3.
Рисунок к вопросу 4
Процессы 1-2 и 3-4 - изохоры, то есть работа на этих участках равна нулю.
Процесс 3-1 изотерма, внутренняя энергия равна нулю.
Работа газа численно равна площади треугольника.
Сравним показатели КПД для 2 атомного газа:
Ответ: для двухатомного газа
5. Определить работу А2 изотермического сжатия газа, совершающего цикл Карно, КПД которого h= 0,4, если работа А1 изотермического расширения равна 8 Дж.
КПД тепловой машины равен отношению производимой работы A к количеству тепла Q1, полученному рабочим телом от нагревателя: .
Совершенная работа равна A=Q1–Q2, где Q2 - количество теплоты, переданное холодильнику. Поэтому .
Полная работа равна сумме работ при изотермическом сжатии (процесс 1-2) и расширении (процесс 3-4): A=A12+A34.
Подставляем числа. A34=(0.4–1)×8кДж=–4.8кДж.
6. Газ, занимающий объем 0,390 м 3 при давлении 155 кПа, изотермически расширяется до десятикратного объема и затем изохорически нагревается так, что в конечном состоянии его давление равно первоначальному. При этом процессе газу сообщается количество тепла, равное 1,50 МДж. Изобразить процесс на диаграмме P,V.Вычислить значение g = СP /СV для этого газа.
Рассмотрим процесс изотермического расширения 1-2. Полученное на этом участке тепло полностью идет на работу газа
Тепло, получаемое на участке 2-3, полностью идет на изменение внутренней энергии газа:
Суммарное тепло, получаемое газом на этапах 1-2-3:
7. Идеальный газ совершает цикл, состоящий из изохоры, адиабаты и изотермы, причем изотермический процесс происходит при минимальной температуре цикла. Изобразить этот цикл на диаграмме P,V. Найти КПД цикла, если температура в его пределах изменяется в n раз.
Изохора, адиабата и изотерма:
Тепло газ получает на участке 1-2:
В токе 2 уравнение состояния газа:
В токе 3 уравнение состояния газа:
Процесс 2-3 - адиабата:
Тепло газ отдает на участке 3-1:
а) при постоянном давлении;
б) при постоянной температуре.
Молекулярная физика и термодинамика Вариант 1
1. При какой температуре средняя квадратичная скорость молекул водорода больше наиболее вероятной скорости на 100 м/с?
2. При расширении газа в цилиндре с поршнем молекулы газа, ударяясь об удаляющийся поршень, отражаются с меньшими скоростями, отдавая поршню часть своей энергии. Приток теплоты компенсирует это уменьшение энергии и увеличивает энергию молекул пропорционально объему. Какой это процесс?
3. Кислород массой m = 250 г, имеющий температуру Т1 = 200 К, был адиабатически сжат. При этом была совершена работа А = 25 кДж. Определить конечную температуру Т2 газа.
4. Сравнить КПД циклов 123 и 134, изображенных на рисунке. Отношение Р2/ Р1 = 2, V2/ V1 = 3.

Рисунок к вопросу 4
5. Определить работу А2 изотермического сжатия газа, совершающего цикл Карно, КПД которого = 0,4, если работа А1 изотермического расширения равна 8 Дж.
6. Газ, занимающий объем 0,390 м 3 при давлении 155 кПа, изотермически расширяется до десятикратного объема и затем изохорически нагревается так, что в конечном состоянии его давление равно первоначальному. При этом процессе газу сообщается количество тепла, равное 1,50 МДж. Изобразить процесс на диаграмме P,V. Вычислить значение = СP /СV для этого газа.
7. Идеальный газ совершает цикл, состоящий из изохоры, адиабаты и изотермы, причем изотермический процесс происходит при минимальной температуре цикла. Изобразить этот цикл на диаграмме P,V. Найти КПД цикла, если температура в его пределах изменяется в n раз.
8. Найти приращение энтропии ΔS при расширении 0,20 г водорода от объема V1 = 0,5 л до объема V2 = 4,5 л, если процесс происходит:
а) при постоянном давлении;
б) при постоянной температуре.
Вариант 2
9. Определить температуру газа, для которой средняя квадратичная скорость молекул водорода больше их наиболее вероятной скорости на ΔV = 400 м/с.
10. При расширении газа в цилиндре с поршнем молекулы газа, ударяясь об отступающий поршень, отражаются с меньшими скоростями, отдавая поршню часть своей энергии. Приток теплоты компенсирует эту убыль энергии. Какой это процесс?
11. В сосуде объемом V = 40 л находится кислород. Температура кислорода T = 300 К. Когда часть кислорода израсходовали, давление в баллоне понизилось на ΔР = 100 кПа. Определить массу израсходованного кислорода, если температура газа в баллоне осталась прежней.
12. Сравнить изменения температуры газа в процессах 1→2 и 2→3, показанных на рисунке, если отношение Р2/ Р1 = 2, V2/ V1 = 2.

Рисунок к вопросу 12
13. Расширяются 14 г азота адиабатически так, что давление уменьшается в пять раз, и затем изотермически сжимаются до первоначального давления. Начальная температура азота T1 = 420 К. Изобразить процесс на диаграмме P, V. Найти:
а) температуру газа T2 в конце процесса;
б) количество тепла, отданного газом;
в) приращение внутренней энергии газа.
14. Газ, совершающий цикл Карно, отдает охладителю 67 % теплоты, полученной от нагревателя. Определить температуру охладителя T2, если температура нагревателя T1 = 430 К.
15. Тепловые машины с произвольным веществом в качестве рабочего тела совершают обратимые термодинамические циклы, показанные на рисунках. Выразить КЦД этих циклов через максимальную T1 и минимальную T2 температуру газов.

Рисунок к вопросу 15
16. В циклическом процессе в газе, показанном ниже на рисунке, ветвь 1→2 – изотерма. На каких стадиях процесса энтропия газа уменьшается?
Задание 12. МКТ, термодинамика. Установление соответствия . ЕГЭ 2022 по физике

С некоторой массой идеального газа был проведён циклический процесс, изображённый на рисунке. Укажите, как менялся объём газа при переходе из 1 → 2 и 4 → 1. Для каждого случая определите соответствующий характер изменения:
| Процессы | Характер изменения |
| A) Процесс 1 → 2 Б) Процесс 4 → 1 | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждого процесса. Цифры в ответе могут повторяться.
Решение
В процессе 1-2 объем газа не менялся, т.к. переход 1-2 - это изохора, покольку его продолжение идет через начало координат. Переход 4-1 - изобара, т.к. $p_1=p_4$, тогда $
Задача 10
В сосуде объёмом V при давлении p и температуре T находится идеальный газ массой m и молярной массой M . Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физические явления | Формулы |
| А) давление газа Б) температура газа | 1) $ 2) $ 3) $ 4) $ |
Решение
Из формул и формулировок МКТ очевидно, что $P=
Задача 11
По мере понижения температуры воды от +40◦С до −20◦С она находилась сначала в жидком состоянии, затем происходил процесс её отвердевания и дальнейшее охлаждение твёрдой фазы воды–льда. Изменялась ли внутренняя энергия воды во время этих процессов и если изменялась, то как? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Отвердевание воды Б) Охлаждение льда | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
1) Отвердевание воды и охлаждение льда два процесса, подчиняющихся первому началу термодинамики, согласно которому внутренняя энергия изменяется при совершении работы или передачи тепла. Следовательно, внутренняя энергия воды уменьшилась в ходе всех двух процессов.
Задача 12
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит шарик. Из сосуда выпускается половина газа при неизменной температуре. Как изменились в результате этого объём газа и действующая на шарик архимедова сила? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Объём газа Б) Архимедова сила | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если у сосуда выпустить половину газа, то атмосферное давление уравновесит давление поршнем и поршень передвинется вниз, вследствие чего, объем газа уменьшится. Архимедова же сила, действующая на шарик, не изменится, поскольку плотность газа под поршнем останется неизменной: $F_<арх>=p_г·g·V_ш$, где $g=9.8м/с^2$ - ускорение свободного падения, $V_ш$ - объем шарика, $p_г$ - плотность газа под поршнем.
Задача 13
Температуру нагревателя тепловой машины уменьшили, оставив температуру холодильника прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и количество теплоты, отданное газом за цикл холодильнику? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) КПД тепловой машины Б) Количество теплоты, отданное газом за цикл холодильнику | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если понизить температуру нагревателя при неизменной температуре холодильника, то КПД идеальной тепловой машины уменьшается в соответствие с уравнением: $η=(1-
Задача 14
Если налить воду в открытый сосуд, то она начнёт испаряться. Как будут меняться при этом её температура и внутренняя энергия? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
При испарении, жидкость покидают наиболее быстрые молекулы, поэтому средняя скорость остальных молекул жидкости становится меньше. Следовательно, и средняя кинетическая энергия остающихся в жидкости молекул уменьшается. Это означает, что температура жидкости и внутренняя энергия испаряющейся жидкости уменьшается.
Задача 15
Ученик наблюдает за процессом кипения воды, нагреваемой в кастрюле на электроплите. Как в процессе кипения меняется температура и внутренняя энергия системы «вода–пар»? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
При кипении, температура системы "вода-пар" остается постоянной, а внутренняя энергия данной системы увеличивается, т.к. происходит поглощение тепловой энергии.
Задача 16
В вертикальном цилиндрическом сосуде под поршнем, способным перемещаться без трения, находится воздух.Как изменятся температура газа и его объём, если поршень быстро сместить вниз? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Объём | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если поршень быстро сместить вниз, то объем газа уменьшится, давление - увеличится, а так как давление связано с температурой соотношением: $p=nkT$, то и температура тоже увеличится.
Задача 17
В вертикальном цилиндрическом сосуде под поршнем, способным перемещаться без трения, находится воздух. Как изменятся давление газа и его внутренняя энергия, если поршень быстро сместить вверх? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Давление Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если поршень сместить вверх, то обмен с окружающейс средой произойти не успеет - процесс будет адиабатным. Тогда из 1 закона термодинамики $Q=0=A+∆U$, тогда $∆U=-A$. Газ расширяется, значит $A>0$, следовательно, и $∆U T_1$, то при повышении температуры воздуха скорость его молекул увеличится, это приведет к увеличению ударов молекул о стенки сосуда и поршня, а следовательно, к увеличению давления, что приведет к тому, что поршень сместится, увеличив объем газа, плотность же газа, уменьшится, поскольку $p=
Тепловое расширение. Газовые законы
В два сосуда конической формы, расширяющихся кверху и книзу, и цилиндрический налита вода при температуре T = 100 °C. Как изменится давление на дно сосудов после охлаждения воды до комнатной температуры?
В сосуде конической формы, расширяющемся кверху, давление на дно увеличится. В сосуде конической формы, расширяющемся книзу, давление на дно уменьшится. В цилиндрическом сосуде давление на дно не изменится.
Две линейки — одна медная, другая железная — наложены одна на другую так, что они совпадают только одним концом. Определить длины линеек при t = 0 °C, зная, что разность их длин при любой температуре составляет Δl = 10 см. Коэффициент линейного расширения меди α1 = 17·10 -6 К -1 , железа — α2 = 12·10 -6 К -1 .
Длина медной линейки 24 см, длина железной — 34 см.
Часы, маятник которых состоит из груза малых размеров и легкой латунной нити, идут правильно при 0 °C. Найти коэффициент линейного расширения латуни, если при повышении температуры до t = +20 °C часы отстанут за сутки на 16 с.
На сколько часы будут уходить вперед за сутки при t0 = 0 °C. если они выверены при t = 20 °C, и материал, из которого сделан маятник, имеет коэффициент линейного расширения α = 0,000012 К -1 ?
При t0 = 0 °С часы спешат в сутки на τ = 20 с. При какой температуре часы будут идти точно? Коэффициент линейного расширения материала маятника α = 1,9·10 -5 К -1 .
Какую силу F надо приложить к стальному стержню сечением S = 1 см 2 , чтобы растянуть его на столько же, на сколько он удлиняется при нагревании на Δt = 1 °С? Коэффициент линейного расширения α = 12·10 -6 К -1 . Модуль Юнга E = 2,1·10 11 Н/м 2 .
Толщина биметаллической пластинки, составленной из одинаковых полосок стали и цинка, равна d = 0,1 см. Определить радиус кривизны r пластинки при повышении температуры на Δt = 11 °С. Коэффициент линейного расширения цинка α1= 25·10 -6 К -1 , а стали α2 = 12·10 -6 К -1 .
Концы стального стержня сечением S = 1 см 2 , находящегося при температуре t = 20 °С, прочно закреплены. С какой силой стержень будет действовать на опоры, если его нагреть до t1 = 200 °С? Модуль Юнга стали E = 2,0·10 11 Н/м 2 , коэффициент линейного расширения α =1,2·10 -5 К -1 ?
F = 39600 Н.
Каково давление газа p0 в электрической лампочке, объем которой V = 1 л, если при отламывании кончика последней под поверхностью воды на глубине h = 1 м в лампочку вошло m = 998,7 г воды? Атмосферное давление нормальное.
Стеклянный баллон объемом V = 1 л был наполнен испытуемым газом до давления p = 10 5 Па и взвешен. Его вес оказался равным Q = 0,9898 Н. Затем часть газа была удалена так, что давление в баллоне упало до р1 = 5·10 4 Па. Новый вес баллона оказался равным Q1 = 0,9800 Н. Какова плотность испытуемого газа при нормальном атмосферном давлении? Температура постоянна.
ρ = 2,1 кг/м 3 .
p1 = 751 мм рт. ст.
Открытую стеклянную трубку длиной l = 1 м наполовину погружают в ртуть. Затем трубку закрывают пальцем и вынимают. Какой длины столбик ртути останется в трубке? Атмосферное давление равно H = 750 мм рт. ст.
В запаянной с одного конца стеклянной трубке длиной l = 90 см находится столбик воздуха, запертый сверху столбиком ртути высотой h = 30 см; столбик ртути доходит до верхнего края трубки. Трубку осторожно переворачивают открытым концом вниз, причем часть ртути выливается. Какова высота столбика ртути, которая останется в трубке, если атмосферное давление H = 750 мм рт. ст.?
В сосуд со ртутью опускают открытую стеклянную трубку, оставляя над поверхностью конец длиной l = 60 см. Затем трубку закрывают и погружают еще на 30 см. Определить высоту столба воздуха в трубке. Атмосферное давление p0 = 760 мм рт. ст.
.
Посередине откачанной и запаянной с обоих концов горизонтальной трубки длиной L = 1 м находится столбик ртути длиной h = 20 см. Если трубку поставить вертикально, столбик ртути сместится на l = 10 см. До какого давления была откачана трубка? Плотность ртути ρ = 1,36·10 4 кг/м.
Расположенная горизонтально запаянная с обоих концов стеклянная трубка разделена столбиком ртути, на две равные части. Длина каждого столбика воздуха 20 см. Давление 750 мм рт. ст. Если трубку повернуть вертикально, ртутный столбик опускается на 2 см. Определить длину столбика ртути.
Цилиндрический сосуд делится на две части тонким подвижным поршнем. Каково будет равновесное положение поршня, когда в одну часть сосуда помещено некоторое количество кислорода, в другую — такое же по массе количество водорода, если длина сосуда l = 85 см?
В закрытом цилиндрическом сосуде с площадью основания S находится газ, разделенный поршнем массой M на два равных отсека. Масса газа под поршнем при этом в k раз больше массы газа над ним. Температуры газов одинаковы. Пренебрегая трением и массой газа по сравнению с массой поршня, найти давление газа в каждом отсеке.
; .
Имеются два мяча различных радиусов, давление воздуха в которых одинаково. Мячи прижимают друг к другу. Какой формы будет поверхность соприкосновения?
Выгнута в сторону мяча с большим радиусом.
Найти число n ходов поршня, которое надо сделать, чтобы поршневым воздушным насосом откачать воздух из сосуда емкостью V от давления p0 до давления p, если емкость насоса ΔV.
.
Упругость воздуха в сосуде равна 97 кПа. После трех ходов откачивающего поршневого насоса упругость воздуха упала до 28,7 кПа. Определить отношение объемов сосуда и цилиндра насоса.
Два баллона соединены трубкой с краном. В первом находится газ при давлении p = 10 5 Па, во втором — при p1 = 0,6·10 5 Па. Емкость первого баллона V1 = 1 л, второго — V2 = 3 л. Какое давление установится в баллонах (в мм рт. ст.), если открыть кран? Температура постоянная. Объемом трубки можно пренебречь.
Три баллона емкостями V1 = 3 л, V2 = 7 л и V3 = 5 л наполнены соответственно кислородом (p1 = 2·10 5 Па), азотом (p2 = 3·10 5 Па) и углекислым газом (p3 = 6·10 4 Па), при одной и той же температуре. Баллоны соединяют между собой, причем образуется смесь той же температуры. Каково давление смеси?
На гладком горизонтальном столе находится сосуд, разделенный перегородкой на две равные части. В одной части сосуда находится кислород, а в другой — азот. Давление азота вдвое больше давления кислорода. На сколько сдвинется сосуд, если перегородка станет проницаемой? Длина сосуда l = 20 см. Массой сосуда пренебречь. Процесс считать изотермическим.
В цилиндре, закрытом легко подвижным поршнем массой m и площадью S, находится газ. Объем газа равен V. Каким станет объем газа, если цилиндр передвигать вертикально с ускорением: а) +a; б) -a? Атмосферное давление равно p0, температура газа постоянна.
а) ; б) .
Начертить графики изотермического, изобарического и изохорического процессов в идеальном газе в координатах p, V; p, T; V, T. Объяснить, почему коэффициент объемного расширения идеальных газов равен термическому коэффициенту давления.
На рисунке изображены две изотермы одной и той же массы газа.

1. Чем отличаются состояния газов, если газы одинаковы?
2. Чем отличаются газы, если температуры газов одинаковы?
Как менялась температура идеального газа — увеличивалась или уменьшалась — при процессе, график которого в координатах p, V изображен на рисунке.

При нагревании газа получен график зависимости давления от абсолютной температуры в виде прямой, продолжение которой пересекает ось p в некоторой точке выше (ниже) начала координат. Определить, сжимался или расширялся газ во время нагревания.
На рисунке дан график изменения состояния идеального газа в координатах p, V.

Представить этот круговой процесс (цикл) в координатах p, T и V, T, обозначив соответствующие точки.
Сколько ртути войдет в стеклянный баллончик объемом 5 см 3 , нагретый до t1 = 400 °С, при его остывании до t2 = 16 °С, если плотность ртути при t = 16 °С равна ρ = 13,6 г/см 3 ?

При какой температуре находился газ, если при нагревании его на Δt = 22 °С при постоянном давлении объем удвоился? Для каких газов это возможно?
До какой температуры нужно нагреть воздух, взятый при t = 20 °С, чтобы его объем удвоился, если давление останется постоянным?
Определить, каким был бы коэффициент объемного расширения идеального газа, если бы за начальный объем его принимали объем не при t0 =0°С, а при t1 = 100 °С?
В цилиндре, площадь основания которого равна S = 100 см 2 , находится воздух при температуре t1 = 12 °С. Атмосферное давление p1 = 101 кПа. На высоте h1 = 60 см от основания цилиндра расположен поршень. На сколько опустится поршень, если на него поставить гирю массой m = 100 кг, а воздух в цилиндре при этом нагреть до t2 = 27 °С? Трение поршня о стенки цилиндра и вес самого поршня не учитывать.
Два одинаковых баллона, содержащие газ при t = 0 °С, соединены узкой горизонтальной трубкой диаметром d = 5 мм, посередине которой находится капелька ртути.

Капелька делит весь сосуд на два объема по V = 200 см 3 . На какое расстояние x переместится капелька, если один баллон нагреть на Δt = 2 °С, а другой на столько же охладить? Изменением объемов сосудов пренебречь.
Два одинаковых сосуда соединены трубкой, объемом которой можно пренебречь. Система наполнена газом и находится при абсолютной температуре T. Во сколько раз изменится давление в такой системе, если один из сосудов нагреть до абсолютной температуры T1, а другой поддерживать при прежней температуре T?
1. В горизонтально расположенном сосуде, разделенном легко подвижным поршнем, находятся с одной стороны от поршня m1 граммов кислорода, а с другой — m2 граммов водорода. Температуры газов одинаковы и равны T0. Каким будет отношение объемов, занимаемых газами, если температура водорода останется равной T0, а кислород нагреется до температуры T1?
2. Вертикально расположенный сосуд разделен на две равные части тяжелым теплонепроницаемым поршнем, который может скользить без трения. В верхней половине сосуда находится водород при температуре T и давлении p. В нижней части — кислород при температуре 2T. Сосуд перевернули. Чтобы поршень по-прежнему делил сосуд на две равные части, пришлось охладить кислород до температуры T/2. Температура водорода осталась прежней. Определить давление кислорода в первом и втором случаях.
На некоторой высоте давление воздуха p = 3·10 4 Па, а температура t = -43 0 С. Какова плотность воздуха на этой высоте?
Определить давление кислорода, масса которого m = 4 кг, заключенного в сосуд емкостью V = 2 м 3 , при температуре t = 29 °С.
Определить удельный объем азота при температуре 27 °С и давлении p = 4,9·10 4 Па.
Определить массу кислорода, заключенного в баллоне емкостью V = 10 л, если при температуре t = 13 °С манометр на баллоне показывает давление p = 9·10 6 Па.
Какова разница в массе воздуха, заполняющего помещение объемом V = 50 м 3 , зимой и летом, если летом температура помещения достигает t1 = 40 °С, а зимой падает до t2 = 0 °С? Давление нормальное.
Сколько молекул воздуха выходит из комнаты объемом V0 = 120 м 3 при повышении температуры от t1 = 15 °С до t2 = 25 °С? Атмосферное давление p0 = 10 5 Па.
Компрессор захватывает при каждом качании V0 = 4 л воздуха при атмосферном давлении p = 10 5 Па и температуре t0 = -3 °С и нагнетает его в резервуар емкостью V = 1,5 м 3 , причем температура воздуха в резервуаре держится около t1 = 45 °С. Сколько качаний должен сделать компрессор, чтобы давление в резервуаре увеличилось на Δp = 1,96·10 5 Па?
На весах установлены два одинаковых сосуда. Один заполнен сухим воздухом, другой — влажным (насыщенный водяными парами) при одинаковых давлениях и температурах. Какой из сосудов тяжелее?
По газопроводу течет углекислый газ при давлении p = 5·10 5 Па и температуре t = 17 °С. Какова скорость движения газа в трубе, если за τ = 5 мин через площадь поперечного сечения трубы S = 6 см 2 протекает m = 2,5 кг углекислого газа?
Из баллона со сжатым водородом емкостью V = 10 л вследствие неисправности вентиля утекает газ. При температуре t1 = 7 °С манометр показывал p = 5·10 6 Па. Через некоторое время при температуре t2 = 17 °С манометр показал такое же давление. Сколько утекло газа?
Какая часть газа осталась в баллоне, давление в котором было равно p = 1,2·10 7 Па, а температура t = 27 °С, если давление упало до p1 = 10 5 Па? Баллон при этом охладился до t1 = -23 °С.
До какой температуры нужно нагреть запаянный шар, содержащий m = 17,5 г воды, чтобы шар разорвался, если известно, что стенки шара выдерживают давление 10 7 Па, а объем шара V = 1 л?
В цилиндре объемом V, заполненном газом, имеется предохранительный клапан в виде маленького цилиндрика с поршнем. Поршень упирается в дно цилиндра через пружину жесткости k.

При температуре T1 поршень находится на расстоянии l от отверстия, через которое газ выпускается в атмосферу. До какой температуры T2 должен нагреться газ в цилиндре, для того чтобы клапан выпустил часть газа в атмосферу? Площадь поршня S, масса газа в цилиндре m, его молярная масса µ. Объем цилиндрика клапана пренебрежимо мал по сравнению с объемом цилиндра.
В баллоне емкостью V = 110 л помещено m1 = 0,8 кг водорода и m2 = 1,6 кг кислорода. Определить давление смеси на стенки сосуда. Температура окружающей среды t = 27 °С.
В сосуде объемом 1 л заключено m = 0,28 г азота. Азот нагрет до температуры T = 1500 °С. При этой температуре α = 30% молекул азота диссоциировано на атомы. Определить давление в сосуде.
В сосуде находится смесь азота и водорода. При температуре T, когда азот полностью диссоциирован на атомы, давление равно p (диссоциацией водорода можно пренебречь). При температуре 2T, когда оба газа полностью диссоциированы, давление в сосуде 3p. Каково отношение масс азота и водорода в смеси?
Оболочка аэростата объемом V = 1600 м 3 , находящегося на поверхности Земли, наполнена водородом на n = 7/8 при давлении p = 101 кПа и температуре t = 15 °С. Аэростат поднялся на некоторую высоту, где давление p1 = 79,3 кПа и температура t1 = 2 °С. Сколько водорода потерял аэростат при своем подъеме в результате расширения газа?
Доказать, что в атмосфере с постоянной температурой независимо от закона изменения давления с высотой подъемная сила воздушного шара с эластичной оболочкой постоянна. Газ из воздушного шара не вытекает. Пренебречь давлением, обусловленным кривизной оболочки.
Линия заданий 12, ЕГЭ по физике

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 8748.

1) не изменится
2) уменьшится
3) увеличится


Верный ответ: 11
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 8780.
А) внутренняя энергия газа \( U(T) \)
Б) объем газа \( V(T) \)
1) \( dT, d = \) 3 Дж/К
2) \( \frac
3) \( at, a = \) 2 ⋅ 10 -5 м 3 /K
4) \( cT, c = \) 20 Дж/К

Верный ответ: 13
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 8812.

1) не изменится
2) уменьшится
3) увеличится


Верный ответ: 11
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 8844.

А) кипение жидкости
Б) нагревание вещества в газообразном состоянии

Верный ответ: 34
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 8876.
8908. При исследовании изопроцессов использовался закрытый сосуд переменного объема, заполненный аргоном и соединенный с манометром. Объем сосуда медленно уменьшают, сохраняя температуру аргона в нем неизменной. Как изменятся при этом внутренняя энергия аргона в сосуде и концентрация его молекул?
Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


Верный ответ: 13
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 8908.
1) не изменится
2) уменьшится
3) увеличится


Верный ответ: 33
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 8940.
А) изотермическое сжатие при \( \nu = const \)
Б) изобарное расширение при \( \nu = const \)
ЗНАЧЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
A = 0 \)
2) \( \Delta U > 0,
A > 0 \)
3) \( \Delta U = 0,
A > 0 \)
4) \( \Delta U = 0,
A Проверить Показать подсказку

Верный ответ: 42
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 8972.
А) адиабатическое сжатие при \( \nu = const \)
Б) изохорное нагревание при \( \nu = const \)
Физика
Для идеального газа, находящегося в сосуде под поршнем , необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
- постоянным остается также количество вещества (газа):
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
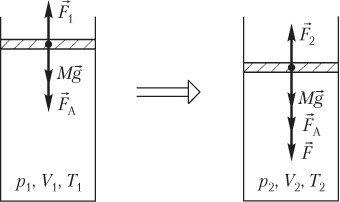
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F → (рис. 5.9).
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p 1 V 1 = ν R T 1 , p 2 V 2 = ν R T 2 , >
где p 1 , V 1 , T 1 — давление, объем и температура газа в начальном состоянии; p 2 , V 2 , T 2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
M g + F A = F 1 , M g + F A + F = F 2 , >
где M — масса поршня; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; S — площадь сечения поршня; F 1 — модуль силы давления газа на поршень в начале процесса, F 1 = p 1 S ; p 1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F 2 — модуль силы давления газа на поршень в конце процесса, F 2 = p 2 S ; p 2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
- если процесс происходит медленно, то температура газа остается постоянной –
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня , закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
- в остальных случаях поршень обладает определенной ненулевой массой —
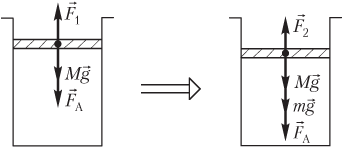
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм 2 и массой 1,80 кг находится 360 см 3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см 3 . Температура газа при его сжатии не изменяется. Определить массу гирь.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 1 , действующая со стороны газа (до его сжатия);
- сила давления газа F → 2 , действующая со стороны газа (после его сжатия);
- m g → — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
где F 1 — модуль силы давления газа, F 1 = p 1 S ; p 1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F 2 = Mg + F A + mg ,
где F 2 — модуль силы давления газа, F 2 = p 2 S ; p 2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
где V 1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
где V 2 — объем сжатого поршнем газа.
p 1 V 1 = p 2 V 2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p 1 S = M g + p A S , p 2 S = M g + p A S + m g , p 1 V 1 = p 2 V 2 , >
которую требуется решить относительно массы гирь m .
Для этого выразим отношение давлений p 2 / p 1 из первой пары уравнений:
p 2 p 1 = M g + p A S + m g M g + p A S
и из третьего уравнения:
p 2 p 1 = V 1 V 2 ,
запишем равенство правых частей полученных отношений:
M g + p A S + m g M g + p A S = V 1 V 2 .
Отсюда следует, что искомая масса определяется формулой
m = ( M + p A S g ) ( V 1 V 2 − 1 ) .
Вычисление дает результат:
m = ( 1,80 + 100 ⋅ 10 3 ⋅ 250 ⋅ 10 − 6 10 ) ( 360 ⋅ 10 − 6 240 ⋅ 10 − 6 − 1 ) = 2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см 2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение . На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 2 , действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
где F 2 — модуль силы давления нагретого газа, F 2 = p 2 S ; p 2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
где p 1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p 1 = p A ; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
где p 2 — давление нагретого газа; T 2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
p A V = ν R T 1 , p 2 V = ν R T 2 , p 2 S = M g + p A S ; >
систему необходимо решить относительно температуры T 2 , до которой следует нагреть газ.
Для этого делением первой пары уравнений
p A V p 2 V = ν R T 1 ν R T 2
получим выражение для давления нагретого газа:
p 2 = p A T 2 T 1
и подставим его в третье уравнение системы:
p A T 2 S T 1 = M g + p A S .
Преобразуем полученное выражение к виду
T 2 = T 1 ( M g + p A S ) p A S = T 1 ( M g p A S + 1 ) ,
а затем найдем разность
Δ T = T 2 − T 1 = M g T 1 p A S .
Δ T = 1,2 ⋅ 10 ⋅ 300 100 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 36 К = 36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см 2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → , действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a → :
F → + F → A + M g → = m a → ,
или в проекции на вертикальную ось —
где F — модуль силы давления газа под поршнем, F = pS ; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a = F − F A − M g M = ( p − p A ) S M − g .
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
и подставим в записанную формулу выражение для модуля ускорения:
v = 2 l ( ( p − p A ) S M − g ) .
v = 2 ⋅ 3,75 ( ( 450 − 100 ) ⋅ 10 3 ⋅ 50 ⋅ 10 − 4 75,0 − 10 ) ≈ 10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Читайте также: