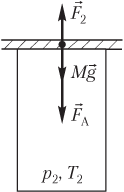Определите давление газа в цилиндре

Обновлено: 09.01.2025

Упражнение 15 - 10 класс, базовый уровень, Мякишев Г.Я. и др.

4. На одинаковые газовые горелки поставили два одинаковых плотно закупоренных сосуда вместимостью по 1 л. В одном сосуде находится вода, а в другом — воздух. Какой сосуд быстрее нагревается до 50 °С? Почему?

5. Предложен следующий проект вечного двигателя (рис. 13.12). Закрытый сосуд разделен на две половинки герметичной перегородкой, сквозь которую пропущены трубка и водяная турбина в кожухе с двумя отверстиями. Давление воздуха в нижней части больше, чем в верхней. Вода поднимается по трубке и наполняет открытую камеру. В нижней части очередная порция воды выливается из камеры турбины, подошедшей к отверстию кожуха. Почему данная машина не будет работать вечно?

6. Положительна или отрицательна работа газа в процессах 1—2, 2—3 и 3—1 на рисунке 10.5? Получает газ тепло или отдает в каждом из этих процессов?

7. Какое количество теплоты необходимо для изохорного нагревания гелия массой 4 кг на 100 К?

8. Вычислите увеличение внутренней энергии водорода массой 2 кг при изобарном его нагревании на 10 К. (Удельная теплоемкость водорода при постоянном давлении равна 14 кДж/(кг• К).)

9. В цилиндре компрессора сжимают идеальный одноатомный газ, количество вещества которого 4 моль. Определите, насколько поднялась температура газа за один ход поршня, если при этом была совершена работа 500 Дж. Процесс считайте адиабатным.

11. Какой должна быть температура нагревателя, для того чтобы стало возможным достижение значения КПД тепловой машины 80%, если температура холодильника 27 °С?

12. В процессе работы тепловой машины за некоторое время рабочим телом было получено от нагревателя количество теплоты (Q1 = 1,5 •10 6 Дж, передано холодильнику Q2 = -1,2 • 10 6 Дж. Вычислите КПД машины и сравните его с максимально возможным КПД, если температуры нагревателя и холодильника соответственно равны 250 °С и 30 °С.

§ 3.12. Примеры решения задач

Если изменяются все три параметра, то следует воспользоваться уравнением состояния в форме (3.9.9) или (3.9.5).

Как измерить медицинским термометром температуру тела человека, если температура окружающего воздуха +42 °С?

Решение. Можно предварительно охладить термометр в холодильнике. Если холодильника нет, то нужно подержать термометр 5—8 мин под мышкой, извлечь его и сразу же стряхнуть. Термометр покажет температуру тела, так как ртуть в термометре сожмется при контакте с телом до объема, соответствующего температуре тела.

Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно р. Определите давление р₁ газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.

Решение. При горизонтальном положении цилиндра объем каждой его части обозначим через V (эти объемы равны). При вертикальном положении цилиндра объем верхней части станет равным V + ΔV, а нижней V - ΔV. Давление в нижней части цилиндра станет равным . Согласно закону Бойля— Мариотта

Исключив из этих равенств , получим квадратное уравнение для p₁:

Второй корень квадратного уравнения отрицателен и потому лишен физического смысла.

Поршневой насос при каждом качании захватывает воздух объемом V₀. При откачке этим насосом воздуха из сосуда объемом V насос совершил п качаний. Затем другой насос с тем же рабочим объемом V₀ начал нагнетать воздух из атмосферы в тот же сосуд, совершив также п качаний. Какое давление установится в сосуде? Температуру воздуха во время работы насоса считать постоянной.

Решение. Согласно закону Бойля—Мариотта при откачке воздуха из сосуда после первого качания давление в сосуде станет равным , где p₀— атмосферное давление.

После второго качания будет выполняться равенство p₁V = p₂(V + V₀) и, следовательно, и т.д. После n качаний в сосуде установится давление

При нагнетании воздуха в сосуд после n качаний давление станет равным

При любом n р > р₀, так как во время нагнетания воздуха при каждом качании насос захватывает воздух, имеющий атмосферное давление р₀, а при откачке при каждом качании удаляется воздух при давлении, меньшем р₀.

В запаянной с обоих концов цилиндрической трубке находится воздух при нормальных условиях. Трубка разделена подвижным поршнем на две части, объемы которых V₁ и V₂ относятся как 1 : 2. До какой температуры t₁ следует нагреть воздух в меньшей части трубки и до какой t₂ охладить в большей, чтобы поршень делил трубку на две равные части, если нагревание и охлаждение в обеих частях трубки производятся при условии = const?

Решение. Условие = const означает, что процессы нагревания и охлаждения происходят изобарно. При отношении начальных объемов эти объемы составляют и , где V₀ — объем всей трубки. Конечные объемы обеих частей одинаковы и равны .

Согласно закону Гей-Люссака для воздуха в меньшей части трубки выполняется соотношение

а для воздуха в большей части

где Т₀ = 273 К — температура, соответствующая начальным условиям. Отсюда

В цилиндре под поршнем находится воздух при давлении p₁ = 2 • 10 5 Па и температуре t₁ = 27 °С. Определите массу m груза, который нужно положить на поршень после нагревания воздуха до температуры t₂ = 50 °С, чтобы объем воздуха в цилиндре стал равен первоначальному. Площадь поршня S = 30 см 2 .

Решение. Так как в процессе нагревания объем воздуха в цилиндре не изменяется, то согласно закону Шарля имеем

Подставляя в (3.12.1) выражение для р₂, получим

Найдите среднюю (эффективную) молярную массу сухого атмосферного воздуха, предполагая известный процентный состав воздуха по массе: азот — n₁ = 75,52%, кислород — n₂ = 23,15%, аргон — n₃ = 1,28% и углекислый газ — n₄ = 0,05%.

Решение. Для каждого газа можно записать уравнение состояния:

Здесь M₁, M₂, M₃ и M₄ — молярные массы соответственно азота, кислорода, аргона и углекислого газа.

Складывая правые и левые части этих уравнений, получим

Для смеси газов выполняется соотношение

где m = m₁ + m₂ + m₃ + m₄ — масса воздуха с объемом V, а М — искомая эффективная молярная масса. Согласно закону Дальтона

Сравнивая уравнения состояния (3.12.2) и (3.12.3), получим

Разделив числитель и знаменатель на m и умножив на 100%, получим выражение для М через процентный состав воздуха по массе

Закрытый с обоих концов цилиндр наполнен газом при давлении p = 100 кПа и температуре t = 30 °С и разделен подвижным теплонепроницаемым поршнем на две равные части длиной L по 50 см. На какую величину ΔT нужно повысить температуру газа в одной половине цилиндра, чтобы поршень сместился на расстояние l = 20 см, если во второй половине цилиндра температура не изменяется? Определите давление газа после смещения поршня.

Решение. Для газа в части цилиндра с постоянной температурой применим закон Бойля—Мариотта:

где S — площадь основания цилиндра. Для нагреваемой части цилиндра запишем уравнение Клапейрона:

В уравнениях (3.12.4) и (3.12.5) р₁ — давление газа после смещения поршня, одинаковое в обеих частях цилиндра вследствие равновесия поршня, а Т + ΔT в уравнении (3.12.5) — температура газа в нагретой части цилиндра.

Разделив почленно уравнение (3.12.4) на уравнение (3.12.5), получим

Из уравнения (3.12.4) находим p₁:

Сосуд объемом V = 100 л разделен пополам полупроницаемой перегородкой. В начальный момент времени в одной половине сосуда находился водород, масса которого m₁ = 2 г, а во второй — 1 моль азота. Определите давления, установившиеся по обе стороны перегородки, если она может пропускать только водород. Температура в обеих половинах одинакова и постоянна: t = 127 °С.

Решение. Так как водород свободно проходит через перегородку, то он распространяется по всему сосуду. Запишем уравнение Менделеева—Клапейрона для водорода после установления состояния равновесия:

где М₁ = 2 • 10 -3 кг/моль — молярная масса водорода.

В той части сосуда, в которой вначале был только водород, он и в дальнейшем останется в чистом виде, так что давление в этой части сосуда станет равным

Для азота уравнение Менделеева—Клапейрона имеет вид

где р₂ — давление азота.

Так как в этой половине находятся водород и азот, то полное давление р согласно закону Дальтона складывается из парциальных давлений р₁ и р₂, т. е.

Гелий массой 20 г, заключенный в теплоизолированном цилиндре под поршнем, медленно переводится из состояния 1 с объемом V₁ = 32 л и давлением р₁ = 4,1 атм в состояние 2 с объемом V₂ = 9 л и давлением р₂ = 15,5 атм. Какой наибольшей температуры достигнет газ при этом процессе, если на графике зависимости давления газа от объема процесс изображается прямой линией (рис. 3.18)?

Решение. Как следует из рисунка 3.18, давление и объем газа связаны линейной зависимостью: р = aV + b, где а и b — постоянные коэффициенты. Из условий задачи получаем систему уравнений

Решив эту систему относительно а и b, найдем

Подставив в уравнение Менделеева—Клапейрона вместо р выражение aV + b, получим

График зависимости Т от V представляет собой параболу (рис. 3.19).

Кривая достигает максимума при V_max = = 20 л, когда корни квадратного уравнения (3.12.6) совпадают. При этом

На рисунке 3.20 изображен график изменения состояния идеального газа в координатах р, V. Начертите графики этого процесса в координатах V, Т и р, Т.

Решение. Из рисунка 3.20 следует, что давление газа р и его объем V находятся в прямой пропорциональной зависимости

где k — постоянный коэффициент. Подставив значение давления (3.12.7) в уравнение Менделеева— Клапейрона, получим

Уравнение (3.12.8) — это уравнение параболы, ось симметрии которой совпадает с осью Т. Следовательно, в координатах V, Т искомый график имеет вид, показанный на рисунке 3.21, а. Аналогично получим график этого процесса в координатах p, T (рис. 3.21, б).

1. Вы надули щеки. При этом и давление, и объем воздуха во рту увеличиваются. Как это согласуется с законом Бойля— Мариотта?
2. Чтобы измерить температуру человеческого тела, приходится держать термометр под мышкой в течение 5—8 мин. В то же время стряхнуть его можно практически сразу после измерения температуры. Почему?
3. Узкая вертикальная трубка длиной L, закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути длиной h. Плотность ртути равна ρ. Трубка расположена открытым концом вверх. Какова была длина l столбика воздуха в трубке, если при перевертывании трубки открытым концом вниз из трубки вылилась половина ртути? Атмосферное давление равно р₀.
4. В ртутный барометр попал пузырек воздуха, вследствие чего барометр показывает давление меньше истинного. При давлении р₁ = 768 мм рт. ст. уровень ртути расположен на высоте h₁ = 748 мм, причем длина пустой части трубки l = 80 мм. Каково атмосферное давление р₂, если ртуть стоит на высоте h₂ = 734 мм? Плотность ртути ρ = 1,36 • 10 4 кг/м 3 .
5. Площадь сечения цилиндра автомобильного насоса S = 10 см 2 . Определите длину l цилиндра, если известно, что для накачки шины объемом V = 0,02 м 3 от давления р₀ = 1 • 10 5 Па до давления р = 3 • 10 5 Па требуется совершить n = 100 качаний. Утечкой и нагреванием воздуха пренебречь.
6. В цилиндре под поршнем находится воздух. Поршень имеет форму, показанную на рисунке 3.22. Масса поршня m = 6 кг, площадь сечения цилиндра S = 20 см 2 . Атмосферное давление р₀ = 10 5 Па. Найдите массу m₁ груза, который надо положить на поршень, чтобы объем V₁ воздуха в цилиндре уменьшился в 2 раза. Трение не учитывать. Температура постоянна.

Силы давления газов

Сила давления газов в цилиндре изменяется в широких пределах в течение цикла и в зависимости от хода поршня определяются из индикаторной диаграммы в координатах р—v или р—ср, построенной по данным расчета цикла двигателя. Здесь р, v — давление и объем цилиндра над поршнем; ср° — угол поворота коленчатого вала. На индикаторной диаграмме проставляются характерные точки, определяющие продолжительность и ориентирование соответствующих процессов относительно ВМТ и НМТ.

На рис. 27 показана индикаторная диаграмма двигателя с принудительным зажиганием в координатах р—v с обозначенными характерными точками: а — конец такта впуска;/—момент подачи искры для зажигания топливо-воздушной смеси; с' — начало воспламенения; ас — такт сжатия; c'z — сгорание (z — теоретическая точка конца сгорания; z_a — действительная точка конца сгорания); zb — такт расширения; Ьг — такт выпуска. Заметим, что после подачи искры в точке /начало воспламенения происходит в точке с', т. е. происходит задержка воспламенения.

Рис. 27. Индикаторная диаграмма двигателя с принудительным зажиганием

Положение точек/и с' относительно ВМТ оказывают огромное влияние на процесс сгорания. Если сгорание смеси начинается слишком рано, создается большое противодавление ходу поршня к ВМТ (линия c'cz), скорость нарастания и максимальное давление оказываГлава 2. Динамика кривошипно-шатунного механизма

ются чрезмерно большими, двигатель перегружается газовыми силами и перегревается, а его мощность и экономичность не достигают оптимальных значений. Для двигателя с принудительным зажиганием возможно возникновение детонации.

Действующая по оси цилиндра сила давления газов Р_г на поршень определяется по формуле

гдер_г — давление газов в цилиндре (давление над поршнем), МПа; р₀ — давление под поршнем, т. е. давление в картере двигателя (для четырехтактных двигателей с вентиляцией картера принимается равным атмосферному давлению, а для двухтактных двигателей с кривошипно-камерной продувкой — равным давлению продувки), МПа; F_n — площадь поршня (поперечного сечения цилиндра), м 2 .

Поскольку давление газов в цилиндре р_т является величиной переменной, то сила давления газов Р_г представляет переменную величину — зависит от хода поршня, объема над поршнем Р_г = f(S_n), Р_г - /₂(v) (см. рис. 27) или Р_г = /₃(ср) — угла поворота коленчатого вала.

Развернутая индикаторная диаграмма в соответствующем масштабе представляет график выражения (1.42), т. е. график силы давления газов в зависимости от угла поворота кривошипа Р_г - /(ф). Она строится с использованием, например, программ Microsoft Excel или разработанной на кафедре «Тепловые двигатели и энергетические установки» ВлГУ программы Dinn. Такая диаграмма необходима для динамического расчета двигателя, а также для расчета на прочность его деталей.

Динамические нагрузки на детали КШМ обусловливаются совместным действием сил давления газов на поршень и сил инерции возвратно-поступательно движущихся масс. Поэтому динамический расчет двигателя на расчетном режиме его работы производится исходя из действия суммарных сил. Исходной при этом является суммарная сила P_s, действующая на поршневой палец вдоль оси цилиндра, которая представляет алгебраическую сумму сил Р_г и Ру. P_s = Р_г + Pj.

Построение графика изменения суммарной силы P_s по углу поворота коленчатого вала ф можно производить графическим суммированием соответствующих ординат графиков сил Р_г = /(ф) и Pj = f (ф). Обычно строят графики удельных сил (в МПа), действующих в кривошипно-шатунном механизме: отношение величины силы к площади поршня F_n (Н/м 2 ). Это позволяет сравнивать нагрузки для двигателей, имеющих различные значения D и S. На рис. 28 приведены графики удельных сил р'_г = Р_т/F_n; p'j = Pj/F_n и p'_s = P_s /F_n для двигателя с принудительным зажиганием на режиме номинальной мощности.

Рис. 28. Графики удельных сил р'_г, р' и p'_s по углу поворота коленчатого вала

Силы давления газов Р_г и Pj считаются приложенными к оси поршневого пальца и имеют положительный знак, если они направлена к оси кривошипа, и отрицательный знак, если они направлены в противоположную сторону (что для Р_г это имеет место лишь при давлении газов в цилиндре меньше р₀ ).

За расчетные режимы в соответствии с обеспечением условий прочности принимают наиболее тяжелые возможные режимы работы двигателей.

Учитывая, что инерционная нагрузка Pj обычно снижает нагрузку от сил давления газов Р_г, другими словами, их совместное действие снижает общую нагрузку P_s, то за основные расчетные принимают три режима:

• • режим максимального крутящего момента (M_em._dX, п_м);
• • режим холостого хода при максимально допустимой частоте вращения коленчатого вала (М_е =0, л_тах);
• • режим максимальной мощности (N_e max, n_N max).

На рис. 29 приведены графики удельных сил р'_г; p'j и p'_s по углу поворота коленчатого вала бензинового двигателя на режиме максимального крутящего момента, а на рис. 30 — те же графики на режиме максимальной частоты вращения холостого хода.

Таким образом, соотношение между силами Р_г и Pj зависит от частоты вращения коленчатого вала.

Рис. 29. Графики удельных сил р'_г, р- и р' по углу поворота коленчатого вала на режиме максимального крутящего момента

Рис. 30. Графики удельных сил р'., pj и p'_s по углу поворота коленчатого вала на режиме максимальной частоты вращения холостого хода

При максимальной частоте вращения холостого хода индикаторная мощность равна мощности трения (7V,- = N_Tp) и силы инерции больше газовых сил.

Определите давление газа в цилиндре

С1-1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь.

С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.

С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.

С1-3. В цилиндре, закрытом подвижным поршнем, находится газ, который может просачиваться сквозь зазор вокруг поршня. В опыте по изотермическому сжатию газа его объем уменьшился вдвое, а давление газа упало в 3 раза. Во сколько раз изменилась внутренняя энергия газа в цилиндре? (Газ считать идеальным.)

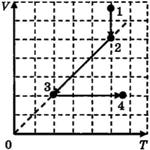
C1-5. Ha V T-диаграмме показано, как изменялись объём и температура некоторого постоянного количества разреженного газа при его переходе из начального состояния 1 в состояние 4. Как изменялось давление газа р на каждом из трёх участков 1—2, 2—3, 3—4: увеличивалось, уменьшалось или же оставалось неизменным? Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.

C1-6. В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают выдвигать из сосуда. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.

С3-9. Нагреваемый при постоянном давлении идеальный одноатомный газ совершил работу 400 Дж. Какое количество теплоты было передано газу?

С3-11. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 8 раз, давление воздуха в сосуде увеличилось в 2 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)

С3-12. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 4 раза, давление воздуха в сосуде увеличилось тоже в 4 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)

С3-13. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q₁ = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔT. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q₂ = 1039 Дж, в результате чего его температура изменилась также на ΔT. Каким было изменение температуры ΔT в опытах? Масса азота m = 1 кг.

С3-14. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q₁ = 742 Дж, в результате чего его температура изменилась на 1 К. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q₂ = 1039 Дж, в результате чего его температура изменилась также на 1 К. Определите массу азота в опытах.

С3-15. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление p = 4 • 10 5 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газа поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной F_тр = 3•10 3 H. Какое количество теплоты получил газ в этом процессе? Считать, что сосуд находится в вакууме.

С3-16. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 10 5 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты │Q│ = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня? Количество вещества газа постоянно.

С3-17. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа р₁ = 4 · 10 5 Па. Расстояние от дна сосуда до поршня равно L. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной F_тp = 3 · 10 3 Н. Найдите L. Считать, что сосуд находится в вакууме.

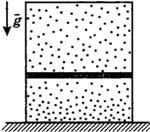
С3-18.Вертикальный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.

С3-19.В вертикальном теплоизолированном цилиндрическом сосуде под поршнем находится 0,5 моль гелия, нагретого до некоторой температуры. Поршень сначала удерживают, затем отпускают, и он начинает подниматься. Масса поршня 1 кг. Какую скорость приобретет поршень к моменту, когда поршень поднимется на 4 см, а гелий охладится на 20 К? Трением и теплообменом с поршнем пренебречь.

С3-20. Теплоизолированный сосуд объемом V = 2 м 3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль Не, а в другой — такое же количество моль А r . Температура гелия Т₁ = 300 К, а температура аргона Т₂ = 600 К. Определите парциальное давление аргона в сосуде после удаления перегородки.

Термодинамика С3-21. На рисунке изображено изменение состояния 1 моль идеального одноатомного газа. Начальная температура газа 27° С. Какое количество теплоты сообщено газу в этом процессе?

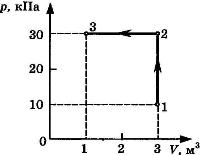
С3-23. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?

С3-24. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?

С3-25. На диаграмме (см. рисунок) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?

Физика

Для идеального газа, находящегося в сосуде под поршнем , необходимо учитывать следующее:

• масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:

• постоянным остается также количество вещества (газа):

• плотность газа и концентрация его молекул (атомов) изменяются:

ρ ≠ const, n ≠ const.

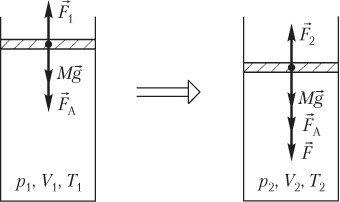
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F → (рис. 5.9).

Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:

p 1 V 1 = ν R T 1 , p 2 V 2 = ν R T 2 , >

где p 1 , V 1 , T 1 — давление, объем и температура газа в начальном состоянии; p 2 , V 2 , T 2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).

Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:

M g + F A = F 1 , M g + F A + F = F 2 , >

где M — масса поршня; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; S — площадь сечения поршня; F 1 — модуль силы давления газа на поршень в начале процесса, F 1 = p 1 S ; p 1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F 2 — модуль силы давления газа на поршень в конце процесса, F 2 = p 2 S ; p 2 — давление газа в сосуде в конечном состоянии.

Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:

• если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —

• если процесс происходит медленно, то температура газа остается постоянной –

Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:

• если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
• в остальных случаях давление газа под поршнем изменяется — p ≠ const.

Масса поршня , закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:

• если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —

• в остальных случаях поршень обладает определенной ненулевой массой —

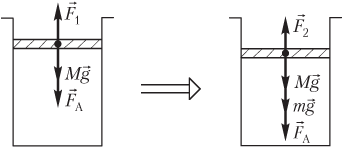
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм 2 и массой 1,80 кг находится 360 см 3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см 3 . Температура газа при его сжатии не изменяется. Определить массу гирь.

Решение . На рисунке показаны силы, действующие на поршень:

• сила тяжести поршня M g → ;
• сила атмосферного давления F → A ;
• сила давления газа F → 1 , действующая со стороны газа (до его сжатия);
• сила давления газа F → 2 , действующая со стороны газа (после его сжатия);
• m g → — вес гирь.

Условие равновесия поршня запишем в следующем виде:

• до сжатия газа —

где F 1 — модуль силы давления газа, F 1 = p 1 S ; p 1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; g — модуль ускорения свободного падения;

• после сжатия газа —

F 2 = Mg + F A + mg ,

где F 2 — модуль силы давления газа, F 2 = p 2 S ; p 2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.

Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:

• до его сжатия —

где V 1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);

• после его сжатия —

где V 2 — объем сжатого поршнем газа.

p 1 V 1 = p 2 V 2

и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:

p 1 S = M g + p A S , p 2 S = M g + p A S + m g , p 1 V 1 = p 2 V 2 , >

которую требуется решить относительно массы гирь m .

Для этого выразим отношение давлений p 2 / p 1 из первой пары уравнений:

p 2 p 1 = M g + p A S + m g M g + p A S

и из третьего уравнения:

p 2 p 1 = V 1 V 2 ,

запишем равенство правых частей полученных отношений:

M g + p A S + m g M g + p A S = V 1 V 2 .

Отсюда следует, что искомая масса определяется формулой

m = ( M + p A S g ) ( V 1 V 2 − 1 ) .

Вычисление дает результат:

m = ( 1,80 + 100 ⋅ 10 3 ⋅ 250 ⋅ 10 − 6 10 ) ( 360 ⋅ 10 − 6 240 ⋅ 10 − 6 − 1 ) = 2,15 кг.

Указанное сжатие газа вызвано гирями массой 2,15 кг.

Пример 20. Открытый цилиндрический сосуд сечением 10 см 2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?

Решение . На рисунке показаны силы, действующие на пластину после нагревания газа:

• сила тяжести пластины M g → ;
• сила атмосферного давления F → A ;
• сила давления газа F → 2 , действующая на пластину со стороны нагретого газа.

Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:

где F 2 — модуль силы давления нагретого газа, F 2 = p 2 S ; p 2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление.

Запишем уравнение Менделеева — Клапейрона следующим образом:

• для газа в сосуде до его нагревания

где p 1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p 1 = p A ; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);

• для газа в сосуде после его нагревания

где p 2 — давление нагретого газа; T 2 — температура нагретого газа.

Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:

p A V = ν R T 1 , p 2 V = ν R T 2 , p 2 S = M g + p A S ; >

систему необходимо решить относительно температуры T 2 , до которой следует нагреть газ.

Для этого делением первой пары уравнений

p A V p 2 V = ν R T 1 ν R T 2

получим выражение для давления нагретого газа:

p 2 = p A T 2 T 1

и подставим его в третье уравнение системы:

p A T 2 S T 1 = M g + p A S .

Преобразуем полученное выражение к виду

T 2 = T 1 ( M g + p A S ) p A S = T 1 ( M g p A S + 1 ) ,

а затем найдем разность

Δ T = T 2 − T 1 = M g T 1 p A S .

Δ T = 1,2 ⋅ 10 ⋅ 300 100 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 36 К = 36 °С.

Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см 2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.

Решение . На рисунке показаны силы, действующие на поршень:

• сила тяжести поршня M g → ;
• сила атмосферного давления F → A ;
• сила давления газа F → , действующая на поршень со стороны нагретого газа.

Под действием указанных сил, направленных вверх, поршень движется с ускорением a → :

F → + F → A + M g → = m a → ,

или в проекции на вертикальную ось —

где F — модуль силы давления газа под поршнем, F = pS ; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.

Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:

a = F − F A − M g M = ( p − p A ) S M − g .

Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением

где l — пройденный путь; v — модуль скорости поршня.

Выразим отсюда модуль скорости поршня:

и подставим в записанную формулу выражение для модуля ускорения:

v = 2 l ( ( p − p A ) S M − g ) .

v = 2 ⋅ 3,75 ( ( 450 − 100 ) ⋅ 10 3 ⋅ 50 ⋅ 10 − 4 75,0 − 10 ) ≈ 10 м/с.

После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.

Идеальный газ в конкурсных задачах

Задача 10 (физфак МГУ им. М.В.Ломоносова, 1973). Найдите работу, совершаемую одним молем идеального газа в цикле 1–2–3–4–1, если известны температуры T₁ и T₃ в точках 1 и 3 соответственно, причём эти точки лежат на одной прямой, проходящей через начало координат.

Решение. Так как работа газа, совершённая им за цикл, равна площади фигуры, ограниченной циклом (только в координатах p, V!), то

В системе уравнений

Так как точки 1 и 3 лежат на прямой, проходящей через начало координат, то или, после следующего уменьшения индекса,

Из этого равенства, а также из второго и четвёртого уравнений последней системы сразу вытекает: T₄ = T₂.

Перемножив почленно первое и третье, а затем второе и четвёртое уравнения системы:

Здесь />= 1 моль. Если просто опустить сомножитель />как равный единице, то получится равенство неверной размерности.

Задачи для самостоятельного решения

Задача 11 (МГТУ им. Н.Э.Баумана). За сколько циклов работы поршневого насоса с объёмом цилиндра V₁ можно откачать газ из стеклянного баллона объёмом V до давления p, если вначале давление в баллоне было равно атмосферному p₀?

Задача 12 (МГТУ им. Н.Э.Баумана). Параметры идеального одноатомного газа, взятого в количестве = 3 моль, изменились по циклу, изображённому на рисунке. Температуры газа в состояниях, отмеченных соответствующими цифрами, равны T₁ = 400 К, T₂ = 800 К, T₄ = 1200 К. Определите работу, которую совершил газ за цикл.

Задача 13 (МГТУ им. Н.Э.Баумана). Моль идеального газа медленно нагревают так, что он переходит из состояния (p₀, V₀) в состояние (2p₀, 2V₀). Как при этом изменяется температура газа T в зависимости от его объёма V, если зависимость давления газа от объёма на графике изображается прямой линией? Определите работу A, совершаемую газом в этом процессе.

Задача 14 (МГТУ им. Н.Э.Баумана). 1 моль идеального газа изменяет своё состояние по циклу, изображённому на рисунке: 4 1 и 2 3 – изохоры, 3 4 – изобара, 1 2 – процесс с линейной зависимостью давления от объёма. Температуры в состояниях 1, 2, 3, 4 равны соответственно T₁, T₂, T₃, T₄. Какую работу совершает газ за один цикл?

Задача 15 (МГТУ им. Н.Э.Баумана). В вертикальном цилиндре площадью поперечного сечения S под поршнем, масса которого равна M, находится 1 моль идеального одноатомного газа. В некоторый момент времени под поршнем включается нагреватель, передающий газу за единицу времени количество теплоты q. Определите установившуюся скорость движения поршня при условии, что давление газа над поршнем постоянно и равно p₀, газ под поршнем теплоизолирован.

Задача 16 (физфак МГУ им. М.В.Ломоносова, 1971). Два одинаковых баллона соединены короткой трубкой, в которой имеется клапан давления, пропускающий газ из одного баллона в другой при разности давлений p 80 см рт.ст. Один баллон наполнен газом, имеющим при температуре T₁ = 290 К давление p = 760 мм рт.ст., в другом баллоне – вакуум. Какое давление установится в баллонах, если их нагреть до температуры T₂ = 382 К?

Задача 17 (МФТИ, 1976). В герметичном сосуде объёмом V = 5,6 л содержится воздух при давлении p = 760 мм рт. ст. Какое давление установится в сосуде, если воздуху сообщить Q = 1430 Дж тепла? Молярную теплоёмкость воздуха при постоянном объёме принять равной C_V = 21 Дж/(моль•К).

Задача 19 (МФТИ, 1981). С какой максимальной силой прижимается к телу человека медицинская банка, если диаметр её отверстия D = 4 см? В момент прикладывания банки к телу воздух в ней прогрет до температуры t = 80 °С, а температура окружающего воздуха t₀ = 20 °С. Атмосферное давление p₀ = 10 5 Па. Изменением объёма воздуха в банке (из-за втягивания кожи) пренебречь.

Задача 20 (МФТИ, 1991). Моль идеального одноатомного газа расширяется сначала в изобарном процессе, а затем в процессе с линейной зависимостью давления от объёма. Известно, что а прямая 2–3 проходит через начало координат. Найдите отношение объёмов , если количество теплоты Q₁₂, подведённое к газу на участке 1–2, в четыре раза меньше работы A₂₃, совершённой газом на участке 2–3.

Как проверить идут ли газы в систему охлаждения

Как проверить идут ли газы в систему охлаждения когда система начинает некорректно работать. И из расширительного бачка выбивает жидкость. Происходить это может по разным причинам.

При прорыве газов из камеры сгорания в систему охлаждения происходит аналогичное действие. Газы скапливаются . образуют полости. Полости не позволяют правильно циркулировать жидкости. Образуются пробки которые не позволяют помпе создавать циркуляцию. Охлаждающая жидкость застаивается перегревается и закипает. В результате выбивает антифриз из расширительного бачка

Газы в системе охлаждения двигателя признаки

Симптомы прорыва газов и закипания жидкости одинаковы. Но все таки суествуют небольшие различия. Именно на начальном этапе необходимо увидеть признаки прорыва газов.

• Газы прорвавшиеся из камеры сгорания в первую очередь скапливаются в самой верхней точке камеры сгорания. Как правило, это радиатор отопителя салона. То есть нарушается циркуляция жидкости в радиаторе отопителя салона. Поэтому постепенно будет снижаться температура воздуха подаваемая из отопителя. Причем во всём остальном. Изменений происходить не будет. Температура системы охлаждения при этом в норме. Жидкость из расширительного бачка выбиваться не будет. Единственное при открытии крышки расширительного бачка сбрасывается небольшое давление. Но определить это как прорвавшиеся газы не получится. Потому что при нагреве пары расширяются и создают небольшое избыточное давление в системе.
• Если внимательно присмотреться внутрь расширительного бачка. Будут видны небольшие пузырьки. Пузырьки эти могут появляться по разному. Они могут возникать на еще не прогретом двигателе. Могут появиться позднее, когда двигатель начнет прогреваться.

Отказ отопителя и появление пузырьков уже говорят о наличии проблемы. В результате выброса газов. Увеличивается давление системы. Из за повышенного давления увеличивается температура закипания жидкости. По принципу скороварки. То есть из за нарушения циркуляции увеличивается температура. а закипания не происходит. В результате резкого снижения давления по причине открывания крышки бачка или лопнувшего патрубка. Происходит мгновенное закипание. Жидкость под большим давлением выбрасывается наружу. Это и является причиной ожогов когда пытаются открыть крышку бачка или радиатора. при возникновении проблем с системой охлаждения. Если обнаружено повышение температуры. Не нужно сразу глушить двигатель. Необходимо дать ему остыть на холостых оборотах. Что бы клапан в крышке бачка справился со сбросом давления постепенно.

Тяжело определить почему закипела жидкость. От прорыва газов или из за неисправностей системы охлаждения. Как проверить идут ли газы в систему охлаждения на самом раннем этапе прорыва. Пока клапан крышки расширительного бачка ещё срабатывает и справляется с повышенным давлением.

При наличии самых первых признаков и нужно бить тревогу. Потому что количество прорывающихся газов будет только увеличиваться.

На первых этапах жидкость не будет поступать в камеру сгорания в местах прорыва газов. Или её поступать будет, но в небольших количествах. Тем более возможно, что при остывании двигателя прорыв вообще устранится до следующего нагрева. На работу двигателя это не окажет практически ни какого влияния. Со временем жидкость будет накапливаться в камере сгорания в больших объемах. И если е накопится достаточно для того чтобы заполнить объём камеры сгорания произойдет гидроудар. Жидкость не сжимается. Поэтому произойдут разрушения гильзы поршня и шатуна.

Повторюсь что на начальном этапе прорыв газов можно определить по наличию пузырьков в расширительном бачке. Нарушениям в работе отопителя. Может быть возникнет подтекание жидкости между головкой и блоком цилиндров. При нагреве в этих местах будет наблюдаться парение жидкости.

Можно использовать механический способ проверки прорыва газов. Если подвести поршень в ВМТ такта сжатия. В свечное отверстие при помощи переходника подать давление воздуха от компрессора. То в случае прорыва газов именно в этом цилиндре. Начнет подниматься уровень жидкости в расширительном бачке. Таким образом, необходимо проверить каждый цилиндр.

На окончательной стадии неисправности. Сомнений не возникает. При увеличении оборотов на не прогретом двигателе жидкость сильно выбивает из расширительного бачка. До этого доводить нельзя.

Единственный эффективный способ как проверить идут ли газы в систему охлаждения на начальном этапе. Это использовать специальную жидкость катализатор. Через неё пропускают газы скопившиеся в расширительном бачке. В случае наличия прорыва газов из камеры сгорания катализатор поменяет цвет. Жидкость катализатора заливается в специальную колбу.

Она имеет две полости. Одну для поступающих газов из расширительного бачка. Другую для заливки катализатора. Газы пропускаются через катализатор. И в случае изменения цвета с уверенностью можно судить о наличии повреждения.

Где прорываются газы в систему охлаждения

Прогорание прокладки гбц

Прогорание прокладки ГБЦ самая распространенная причина прорыва газов в систему охлаждения. В результате перегрева происходит либо ослабление крепежных болтов. Либо проседание прокладки. Или проседание посадочных мест болтов. Возникают ослабленные места . Через которые начинают прорываться газы. Сначала незначительное количество. Этого хватает для того чтобы создать пробки в системе. Появляются незначительные выделения пузырьков газов в расширительном бачке. Раскаленные газы постепенно начинают прожигать прокладку. А иногда даже и поверхность прилегании головки блока. В результате увеличивается объём газов попавших в систему. Это вызывает более бурное выдавливание охлаждающей жидкости. Возникает вероятность проникания жидкости в камеру сгорания уже при неработающем двигателе. Это и приводит к серьёзным разрушениям двигателя.

Трещины в гильзах

В гильзе может образоваться трещина. Которая также разрастается и увеличивает прорыв газов.

Трещины образуются в основном из за местного перегрева. Который происходит из за нарушения подачи топлива. Или от неправильно выставленного угла опережения зажигания. Так же причина может возникнуть из за некачественного топлива. Топливо полностью не сгорает в камере в такте расширения. Продолжает догорать в последующих тактах работы двигателя. При поступлении нового количества топлива его становится больше. Температура повышается. Образуется местный перегрев. Так же он вызывает и прогорание прокладки ГБЦ. И клапанов и поршней.

Проседание гильз

На многих автомобилях в основном грузовых. Гильзы съёмные. Они проседают на своих посадочных местах неравномерно по отношению друг к другу.

Это ослабляет затяжку ГБЦ. И как результат сначала небольшой прорыв газов, потом прогорание прокладок. Эта проблема особенно актуальна на двигателях ЯМЗ

Прорыв газов из под головки двигателя Камаз

Самый курьёзный прорыв газов приходилось наблюдать на автомобиле Камаз. На двигателе головки раздельные. Они прижимаются к гильзам при помощи компрессионного кольца. Система охлаждения между головкой и блоком уплотняется при помощи резиновых присосок.

При прорыве через кольцо газы попадали на это уплотнение. Продавливали его и проникали под давлением в систему охлаждения. Хотя течи жидкости в этом месте не наблюдалось. В результате жидкость выдавливалась из расширительного бачка под большим давлением.

Поэтому методы как проверить идут ли газы в систему охлаждения лучше всего применять на начальном этапе их прорыва. Что бы не вывести из строя двигатель.

Читайте также:

  
• Глохнет на ходу крайслер пацифика
  
• Замена бокового стекла nissan teana
  
• Как работает полный привод на форд эксплорер 5
  
• Установка aux приус 20
  
• Фильтр воздушный шевроле лачетти какой лучше