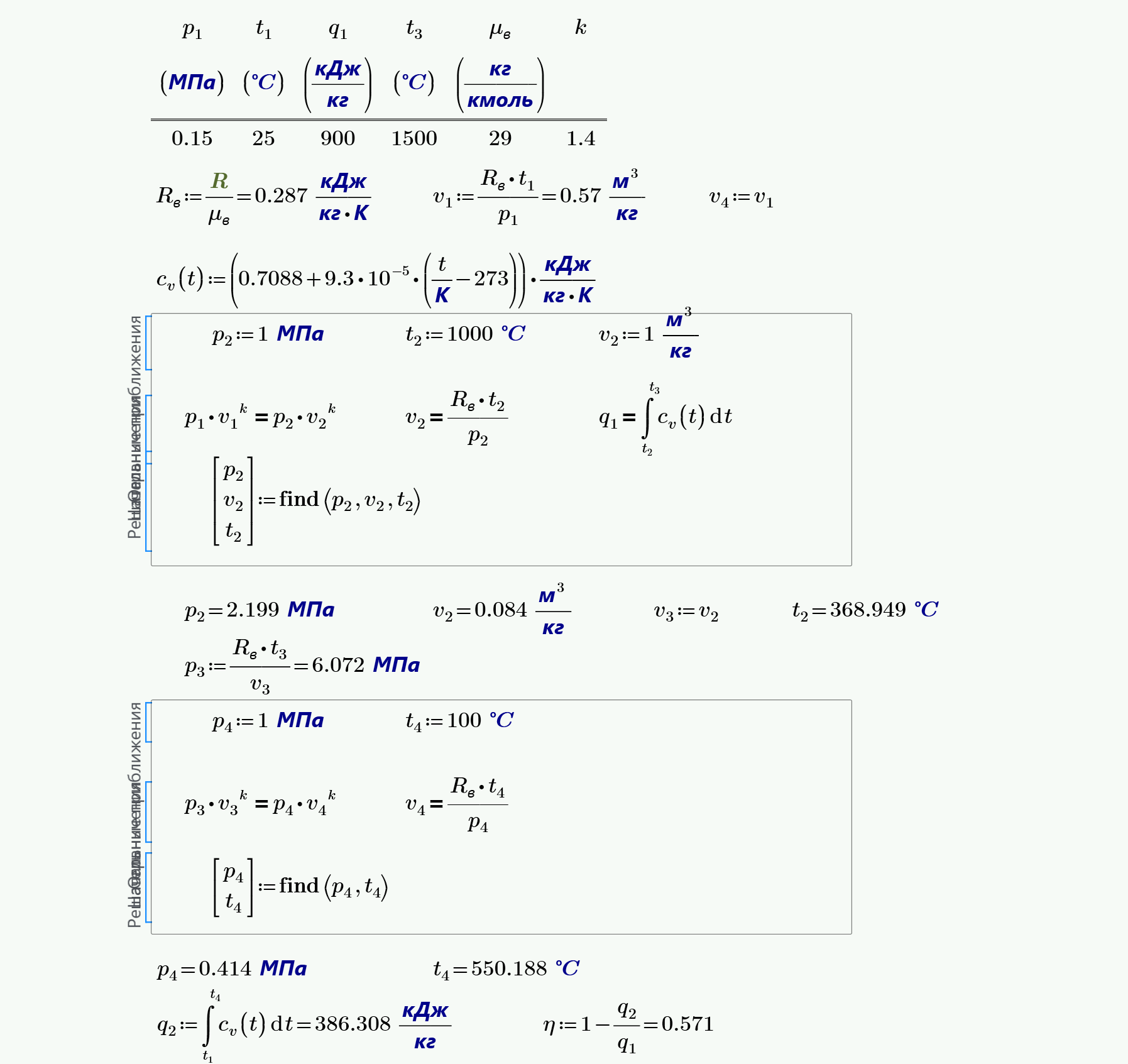
Определить количество теплоты отдаваемое каждым килограммом отработавших газов дизеля
Тепловой баланс дизельного двигателя с наддувом
Q = GтQ н = 0,00529×42,438×10 3 = 224,50 кВт.
Теплота, превращенная в полезную работу (89),
Теплота, передаваемая охлаждающей среде, определится по
формуле (91):
где с - коэффициент пропорциональности, с = 0,45…0,53 для четырехтактных двигателей; поскольку двигатель с наддувом, примем с = 0,5
i= 4 - число цилиндров;
D= 12см - диаметр цилиндра;
n = 2500 мин -1 - заданная частота вращения коленчатого вала двигателя;
m - показатель степени, m = 0,5…0,7 для четырехтактных двигателей, примем m = 0,65.
Теплота теряемая с отработавшими газами (92):
где Gт = 0,00539 кг/с — расход топлива;
Мпс = 0,832 и aМ0 = 0,794— расходы продуктов сгорания и воздуха в расчете на 1 кг топлива, кмоль/кг;
t6 = (Т6 – 273) =801 - 273 =528 о С и tк = (Тк – 273) = 361 – 273 = 88 о С — температуры отработавших газов и поступающего воздуха,;
Остаточный член теплового баланса (94)
Qост = Q – (Qe + Qохл + Qг ) = 224,50 – 85 –59,70 - 77,66 = 3,14кВт.
Таблица 9 - Основные величины теплового баланса двигателя
| Составляющие теплового баланса | Q, кВт | q, % |
| Количество располагаемой (введенной) теплоты | 224,50 | 100 |
| Теплота, превращенная в полезную работу | 85 | 37,86 |
| Теплота, потерянная с охлаждающим агентом | 59,70 | 26,59 |
| Теплота, потерянная с отработавшими газами | 77,66 | 34,59 |
| Остаточный член теплового баланса | 3,14 | 1,40 |
Тепловой расчет карбюраторного двигателя
Выполнить тепловой расчет четырехтактного карбюраторного двигателя. Двигатель четырехцилиндровый (i=4). Система охлаждения жидкостная закрытого типа.
Исходные данные:
- мощность двигателя при n = 5200 об/мин, Nе – 65 кВт;
- топливо - бензин (С = 0,855; Н = 0,145; Н/С=0,17);
Определить:
- количество воздуха, участвующего в сгорании 1 кг топлива;
- количество (кмоль) свежей смеси и продуктов сгорания;
- параметры (р и Т) процессов впуска, сжатия, сгорания и расширения;
- среднее эффективное давление цикла;
- механический, индикаторный и эффективный КПД;
- индикаторный, эффективный и секундный расходы топлива.
Рассчитать тепловой баланс.
Решение:
Низшая теплота сгорания Q Н = 33,913С + 102,995Н – 10,885(О – S) – 2,512d = 33,913×0,855 + 102,995×0,145 = 43,930 МДж/кг = = 43930 кДж/кг.
1. Рассчитаем теоретически необходимое количество воздуха для сгорания 1 кг топлива (15-16):
3. По формуле (19) определим суммарное количество кмоль горючей смеси, участвующей в сгорании 1 кг топлива:
Суммарное количество горючей смеси в килограммах будет равно:
GT =1 + 14,96 = 15,96 кг.
4. Определим суммарное количество продуктов сгорания, которое получается при сгорании этой горючей смеси:
Количество отдельных составляющих продуктов сгорания на 1 кг топлива рассчитываем по (29-33) принимая отношение количества молей не прореагировавшего водорода к числу молей окиси углерода К = 0,5
Изменение количества молей смеси
5. Расчет параметров процесса впуска
Найдем давление в конце впуска:
Рассчитаем коэффициент остаточных газов:
Определим температуру конца впуска:
Найдем величину коэффициента наполнения:
6. Рассчитаем параметры процесса сжатия. Показатель политропы сжатия в зависимости от числа оборотов n:
Давление в конце процесса сжатия:
Температура в конце процесса сжатия:
7. Определим параметры в конце процесса сгорания. Вычислим действительный коэффициент молекулярного изменения (46)
Определим не выделившуюся теплоту вследствие неполного сгорания топлива (согласно формуле (28) А = 114×10 6 )
Найдем температуру в конце процесса сгорания (T3). Для этого воспользуемся уравнением сгорания (48):
Примем коэффициент теплоиспользования теплоты, согласно опытным данным для карбюраторных двигателей, равным 0,85.
Внутренняя энергия 1 кмоля свежей смеси в конце процесса сжатия:
Внутренняя энергия 1 кмоля продуктов сгорания в конце процесса сжатия где
Подставляя найденные значения в уравнение сгорания, получим
Рассчитаем давление в конце процесса сгорания (51)
Степень повышения давления при горении топливной смеси
Действительное максимальное давление в цикле (53)
8. Рассчитаем параметры процесса расширения. Примем показатель политропы расширения n2 = 1,24 (см. табл. 5, стр.33). Давление в конце процесса (56):
Температура в конце процесса расширения (57):
Проверяем правильность ранее принятого значения температуры остаточных газов (погрешность не должна превышать 10% для всех скоростных режимов работы двигателя). Обратить внимание на то, что в циклах бензиновых двигателей т.5 соответствует параметрам остаточных газов в камере сгорания.
что вполне допустимо.
9. Определим среднее индикаторное давление цикла (65)
10. Рассчитаем показатели экономичности цикла. Определим долю индикаторного давления, затраченного на трение и привод вспомогательных механизмов (73), примем S = 0,082 м, тогда средняя скорость поршня (74)
где А и В - коэффициенты, зависящие от конструктивных особенностей двигателя.
Рм = 0,034 + 0,0113Сm = 0,034 + 0, 0113×14,21= 0,194 МПа.
Тогда среднее эффективное давление цикла
Рe = Pi - Рм= 0,994 - 0,194 = 0,80 МПа.
Определим механический КПД (76)
Вычислим удельный индикаторный расход топлива (69)
Тогда удельный эффективный расход топлива (77)
Найдем величину индикаторного КПД
Эффективный КПД цикла (76)
Определим секундный расход топлива
11.Основные параметры цилиндра и двигателя
Определяем литраж двигателя (78):
где t = 4 - тактность двигателя;
Nе- эффективная мощность двигателя.
Определяем рабочий объем одного цилиндра (79):
Vh = Vл / i = 0,001875 / 4=0,000469 м 3 = 0,469 л.
Определяем диаметр цилиндра. Так как ход поршня S предварительно был принят 0,082 м то (80):
Окончательно принимаем D = 0,086 м и S = 0,082 м.
Основные параметры и показатели двигателя определяем по окончательно принятым значениям D и S (81)
Определяем площадь поршня (82):
Определяем эффективную мощность (83):
Определяем эффективный крутящий момент (84):
11. Сравниваем полученное значение мощности с заданным значением (86), делаем выводы о правильности проведенного теплового расчета. Расхождение в значении мощности не должно превышать 10%.
Клуб студентов "Технарь". Уникальный сайт с дипломами и курсовыми для технарей.
Описание:
№1
Какое массовое количество воздуха должно быть подано компрессором в резервуар объемом 3 м3, чтобы при постоянной температуре t1 = -300С и барометрическом давлении 750 мм рт. ст. давление по манометру в нем повысилось от p1=0,8 МПа до p2=2,5 МПа .
№3
Найти затрату теплоты на нагревание объема воздуха V=7м3, при постоянном давлении 750 мм. рт. ст., если начальная температура воздуха t1=500С, а конечная — t2=6500С. Определить объем воздуха в конце процесса нагревания. Процесс изменения состояния воздуха изобразить в pV- и Ts- координатах. Для объемной средней теплоемкости воздуха при нормальных физических условиях принять линейную зависимость cvpm=1,2866+0,00012*t, кДж/(м3*К).
№4
Определить газовую постоянную, среднюю (кажущуюся) молекулярную массу смеси идеальных газов, если ее массовый состав следующий, %: СО2 -18, О2- 12 и N2 -70. Определить также удельный объем и плотность смеси при абсолютном давлении 1Мпа и температуре t1=4500С. Найти среднюю массовую теплоемкость смеси при постоянном давлении в интервале от t1 до t2=9000С.
№8
Требуется определить количество теплоты, отдаваемое каждым килограммом отработавших газов дизеля в утилизированном котле где газы при постоянном давлении охлаждаются от температуры t1=4900С до t2=2900С . Объемный состав отработавших газов rco2=0,08; rH2O=0,06; rO2=0,10; rN2=0,76.
№10
До какого давления надо сжать воздух в политропном процессе со средним показателем n=1,3 в цилиндре двигателя внутреннего сгорания (дизеля) при начальном абсолютном давлении р1=90 кПа и температуре t1=107°С, чтобы достигнуть температуры воспламенения топлива t2=650°С? Определить также работу, затрачиваемую на сжатие, и количество отводимой теплоты, отнесенных к 1 кг воздуха. Теплоемкость воздуха считать не зависящей от температуры.
№15
Воздух, имея начальную температуру t1=27°С и абсолютное давление р1=1,2 МПа изотермически расширяется до давления р2=0,1 МПа, а затем нагревается в изохорном процессе до тех пора, пока давление не станет р1.Требуется определить удельный объем воздуха в конце изохорного подвода теплоты, а так же изменения значений внутренней энергии, энтальпия и энтропия в изохорном процессе .Теплоемкость воздуха считать не зависящей от температуры. Изобразить процессы в P-V T-S диаграммах.
№16
В паронагревателе котельного агрегата за счет подведенной теплоты q=570 кДж/кг 1кг водяного пара при постоянном давлении р=10Мпа температура пара повысилась до t=460°С. Определить постоянные пара и его параметры до пароперегревания(температуру, удельный объем, энтальпию и энтропию и внутреннюю энергию). Решение задачи иллюстрировать i-s диаграммой.
Расчет и построение теплового баланса двигателя
Расчет составляющих теплового баланса ведем в зависимости от частоты вращения для режима работы двигателя с полной нагрузкой, используя при этом данные расчета внешней скоростной характеристики, приведенные в таблице 6.
Общее количество теплоты, вводимое в двигатель с топливом в единицу времени определяем по формуле
Теплота, расходуемая на совершение эффективной работы в единицу времени, равна
Теплота, передаваемая охлаждающей среде, определяется по формуле
где с – коэффициент пропорциональности, принимаем с = 0,5;
m – показатель степени, принимаем для четырехтактного КБД– m = 0,63;
Теплоту, уносимую из двигателя с отработавшими газами, определяем по формуле
где – средняя мольная теплоемкость остаточных газов при р = const и температуре trx °C, кДж/кмоль·град;
– средняя мольная теплоемкость остаточных газов при р = const и температуре t = t0, кДж/кмоль·град;
М1х и М2х – количество свежего заряда и отработавших газов, определяемые в зависимости от aх по формулам, приведенным в п. 2:
trx – температура отработавших газов, изменяющаяся с изменением частоты вращения, °С.
Для выполнения дальнейших расчетов необходимо задаться законом изменения температуры отработавших газов по частоте вращения, учитывая при этом, что с уменьшением частоты вращения от пN до nmin температура отработавших газов уменьшается на 150. 250° приблизительно по линейной зависимости. Тогда промежуточные значения trx определим по выражению
где trN – температура отработавших газов при номинальной частоте вращения, принята в п. 3 равной trN = Тr – 273 = 777 °C;
tr.min – температура отработавших газов при минимальной частоте вращения, tr.min = trN – (150°…250°) = 577 °С;
Средние мольные теплоемкости в уравнении (102) определяем по выражениям:
При определении теплоемкости отработавших газов, при V = const предварительно по формулам (24) – (28), подставляя в них вместо tc значение trx, определяем теплоемкости отдельных компонентов отработавших газов:
Зная величины средних мольных теплоемкостей отдельных компонентов, найдем искомую среднюю мольную теплоемкость по формуле (29)
а затем по формуле (104) найдем
Теплоемкость свежего заряда определяют по формуле (23), в которую вместо температуры tc подставляют значение t = t0 = 20 °С :
а затем по формуле (105) найдем
Теперь определим теплоту, уносимую отработавшими газами по формуле (102):
Рассчитываемый двигатель работает на обогащенных смесях при a < 1, в связи с чем топливо сгорает не полностью, а теряемую при этом теплоту определяем по формуле
Остаточный член теплового баланса, учитывающий потери теплоты отданной маслу, теряемой из-за лучеиспускания в окружающую среду и теплоту, соответствующую кинетической энергии отработавших газов, равен
Результаты расчета сводят в таблицу 7 и по этим данным строим тепловой баланс двигателя в виде графической зависимости процентного содержания каждой составляющей баланса в общем количестве введенной в двигатель теплоты от частоты вращения коленчатого вала двигателя (см. приложение 4).
Таблица 7 – Составляющие теплового баланса двигателя
| nx, мин -1 | Qe | Qв | Qr | Qнс | Qост | Qo | |||||
| кДж/с | % | кДж/с | % | кДж/с | % | кДж/с | % | кДж/с | % | кДж/с | % |
| 12,45 | 25,2 | 15,87 | 32,2 | 10,73 | 21,8 | 10,09 | 20,5 | 0,18 | 0,40 | 49,33 | |
| 26,72 | 28,4 | 25,83 | 27,5 | 22,61 | 24,1 | 6,63 | 7,1 | 12,22 | 13,0 | 94,01 | |
| 41,08 | 30,5 | 33,35 | 24,8 | 34,47 | 25,6 | 9,50 | 7,1 | 16,20 | 12,0 | 134,60 | |
| 53,80 | 30,9 | 39,98 | 23,0 | 47,31 | 27,2 | 12,29 | 7,1 | 20,78 | 11,9 | 174,15 | |
| 63,15 | 29,4 | 46,01 | 21,4 | 61,66 | 28,7 | 15,15 | 7,1 | 28,73 | 13,4 | 214,70 | |
| 67,40 | 26,6 | 51,61 | 20,3 | 76,83 | 30,3 | 17,91 | 7,1 | 40,02 | 15,8 | 253,76 | |
| 67,49 | 26,0 | 52,47 | 20,2 | 79,16 | 30,5 | 18,30 | 7,1 | 41,90 | 16,2 | 259,31 | |
| 64,80 | 23,1 | 56,88 | 20,3 | 89,39 | 31,8 | 19,81 | 7,1 | 49,93 | 17,8 | 280,81 |
Заключение
Проведенные расчеты показали, что для увеличения мощности двигателя и частоты вращения коленчатого вала ход поршня должен быть равным S = 86 мм, диаметр цилиндра D = 80 мм. При этом литраж двигателя будет равен Vл = 1,7291 л, эффективная мощность Ne = 67,486 кВт, литровая мощность Nл = 39,029 кВт/л, эффективный крутящий момент Ме = 104,62 Н×м и часовой расход топлива GТ = 21,250 кг/ч.
Определить количество теплоты отдаваемое каждым килограммом отработавших газов дизеля
Главное меню
Судовые двигатели
Главная Судовые двигатели внутреннего сгорания Идеальные циклы и тепловые процессы в двигателях Тепловой баланс работы двигателяКак это следует из рассмотрения рабочего цикла двигателя, тепло, выделяющееся при сгорании топлива, не все переходит в полезную механическую работу — часть тепла уносится с охлаждающей водой, с отработавшими газами, а также незначительная часть тепла теряется от неполноты сгорания топлива в окружающую среду и переходит в тепло, эквивалентное кинетической энергии выпускных газов (если она не используется). Тепловой баланс двигателя (рис. 150) распределяет тепло, выделившееся при сгорании топлива, по статьям его расхода. Составляется тепловой баланс двигателя при различных режимах его работы по данным испытаний. Обычно составляют удельный тепловой баланс, т. е. отнесенный к 1 э. л. с. ч в ккал или в процентах.
Уравнение удельного теплового баланса состоит из следующих слагаемых:
где q т — располагаемое тепло топлива, вводимого в цилиндр двигателя,
q e — тепло, превращенное в эффективную работу 1 л. с. в течение 1 ч;
q охл — тепло, уносимое охлаждающей водой;
q г — тепло, уносимое отработавшими газами;
q н . б — невязка баланса, равная сумме остальных неучтенных потерь. Слагаемые уравнения теплового баланса равны:
где G охл — расход охлаждающей воды в кг/ч;
t 1 и t 2 — температуры охлаждающей воды при входе и выходе из двигателя;
с ? — теплоемкость воды.
Количество тепла, эквивалентное работе трения движущихся деталей двигателя, передается охлаждающей воде, циркулирующей в полостях охлаждения и в маслохолодильнике, а потому отдельно не учитывается. Количество тепла от трения, не перешедшее в охлаждающую воду, включается в невязку баланса.
Тепло, уносимое отработавшими газами,
где Т г и Т 0 — температуры отработавших газов в выпускном коллекторе и свежего заряда, поступающего в цилиндр в °К.
Значение q г можно определить, пользуясь приближенной формулой для подсчета тепла, уносимого отработавшими газами 1 кг сгоревшего топлива:
Остаточный член теплового баланса — невязка баланса определяется как разность
Рассмотренное распределение тепла определяет так называемый внешний тепловой баланс, который обычно составляется при испытании двигателя. Распределение тепла, выделяемого в цилиндре, на слагаемые, учитывающие тепло, превращенное в индикаторную работу, тепло, переданное охлаждающей воде в различные периоды цикла, тепло, уносимое с отработавшими газами, тепло, потерянное вследствие неполноты сгорания, тепло, отданное в окружающую среду, и тепло, эквивалентное кинетической энергии отработавших газов, называется внутренним тепловым балансом двигателя. На рис. 150 показана схема внешнего теплового баланса двигателя с разбивкой слагаемых его на отдельные внутренние составляющие, к числу которых относятся: q i —тепло, эквивалентное индикаторной работе; q c т — тепло, передаваемое стенкам двигателя; q мех — тепло, эквивалентное механическим потерям; q вг — тепло, эквивалентное полной энергии выпускных газов, q тр — тепло, эквивалентное работе трения поршня и поршневых колец; q кин — тепло, эквивалентное кинетической энергии выпускных газов; q л — тепло, теряемое в окружающую среду; q н . сг — тепло, эквивалентное неполноте сгорания топлива; q кол — тепло, переданное в охлаждающую воду в выпускном коллекторе.
Современные судовые дизели имеют следующие значения слагаемых теплового баланса при номинальном режиме их работы: q е = 35?45%; q охл = 15?28%; q г = 25?50%; q н . б = 1?8%.
При форсировке двигателя, как по числу оборотов, так и по среднему эффективному давлению удельный унос тепла охлаждающей водой уменьшается, а удельный унос тепла выпускными газами возрастает. Объясняется это тем, что с увеличением нагрузки и числа оборотов вала двигателя продолжительность процесса сгорания возрастает за счет догорания его на линии расширения.
Тепловой баланс двигателя
Тепловой баланс двигателя характеризует распределение теплоты, выделяемой при сгорании топлива, вводимого в цилиндры двигателя на полезно используемую и отдельные виды потерь характеризуется внешним тепловым балансом. Характер распределения теплоты сгорания по составляющим внешнего теплового баланса определяется особенностями рабочего процесса, а также геометрическими размерами цилиндропоршневой группы, конструкцией деталей и системы охлаждения.
Внешний тепловой баланс в целом и отдельные его составляющие в частности позволяют оценить показатели теплонапряженности деталей двигателя, рассчитать систему охлаждения, определить резервы в использовании теплоты обработавших газов и пути повышения экономичности двигателя.
Общее количество теплоты
Общее количество теплоты Q в кДж/ч, введенной в двигатель с топливом находим по формуле:
где Gт - часовой расход топлива.
Qn-низшая удельная теплота сгорания.
Часовой расход топлива Gт в кг/ч находится по формуле:
- для дизельного топлива:
Низшая удельная теплота сгорания Qн=42500 кДж/кг.
Низшая удельная теплота сгорания Qн=37300 кДж/кг.
Теплота, эквивалентная эффективной работе
Теплота, эквивалентная эффективной работе Qe в кДж/ч найдем из выражения:
где Ne - эффективная мощность, кВт; для двигателя Д-21 Ne=15 кВт.
- для дизельного топлива:
Процентное количество тепла qе в%, расходуемая на совершение работы:
Найдем процентное количество тепла qе:
Теплота передаваемая охлаждающей среде
Теплота Qв в кДж/ч передаваемая охлаждающей среде для дизелей без наддува:
где C - коэффициент, равный 0,45…0,53
i - число цилиндров;
D - диаметр цилиндра, см;
n - частота, вращения коленчатого вала, мин -1 ;
- коэффициент избытка воздуха.
С=0,45; i=2; D=10,5 см; n= 1600 мин -1 ; =1,65.
Зная все величины найдем, теплоту передаваемую охлаждающей среде Qв:
Процентное количество тепла qe в%, передаваемое охлаждающей среде найдем по формуле:
Найдем количества теплоты qe:
Примем коэффициент избытка воздуха =1,2:
Теплота, уносимая с отработавшими газами
Теплота Qв в кДж/ч, уносимая с отработавшими газами находится по формуле:
где Ср - средняя теплоемкость отработавших газов при постоянном давлении;
Средняя теплоемкость равно Ср - 1,04 кДж/кгград;
Тr и То - температуры отработавших газов и окружающей среды, К;
- для дизельного топлива;
Берем из предыдущих расчетов Тr = 850 К; То = 293 К;
Gв и Gт - количества поступившего в цилиндр воздуха и топлива, кг/ч;
Количества поступившего в цилиндр воздуха Gв в кг/ч найдем из выражения:
где Gт-часовой расход топлива, кг/ч; Gт=3,3635
Подставив часовой расход топлива Gт найдем Gв:
Подставив значения в уравнение (3.41) вычислим Qr:
Qr= 1,04850-29378,05-3,2625=40210 кДж/ч
Процентное количество теплоты qr в%, уносимое с отработавшими газами:
Найдем количество теплоты qr:
Температура выхлопных газов Тr = 700 К;
Qr= 1,04700-29376,3-4,39=30438 кДж/ч;
Неучтенные потери теплоты
Неучтенные потери Qн.у. в кДж/ч находятся по формуле:
Найдем неучтенные потери Qн.у.:
Процентное количество тепла qн.у в% на неучтенные потери находим по выражению:
Energy
education
Термодинамические циклы — круговые процессы в термодинамике, то есть такие процессы, в которых совпадают начальные и конечные параметры, определяющие состояние рабочего тела.
Примеры решения задач по теме "Циклы газовых двигателей"
1. К газу в круговом процессе подведено $250$ кДж теплоты. Термический КПД равен $0.46$. Определить работу, полученную за цикл.
2. В результате осуществления кругового процесса получена работа, равная $80$ кДж, а отдано охладителю $50$ кДж теплоты. Определить термический КПД цикла.
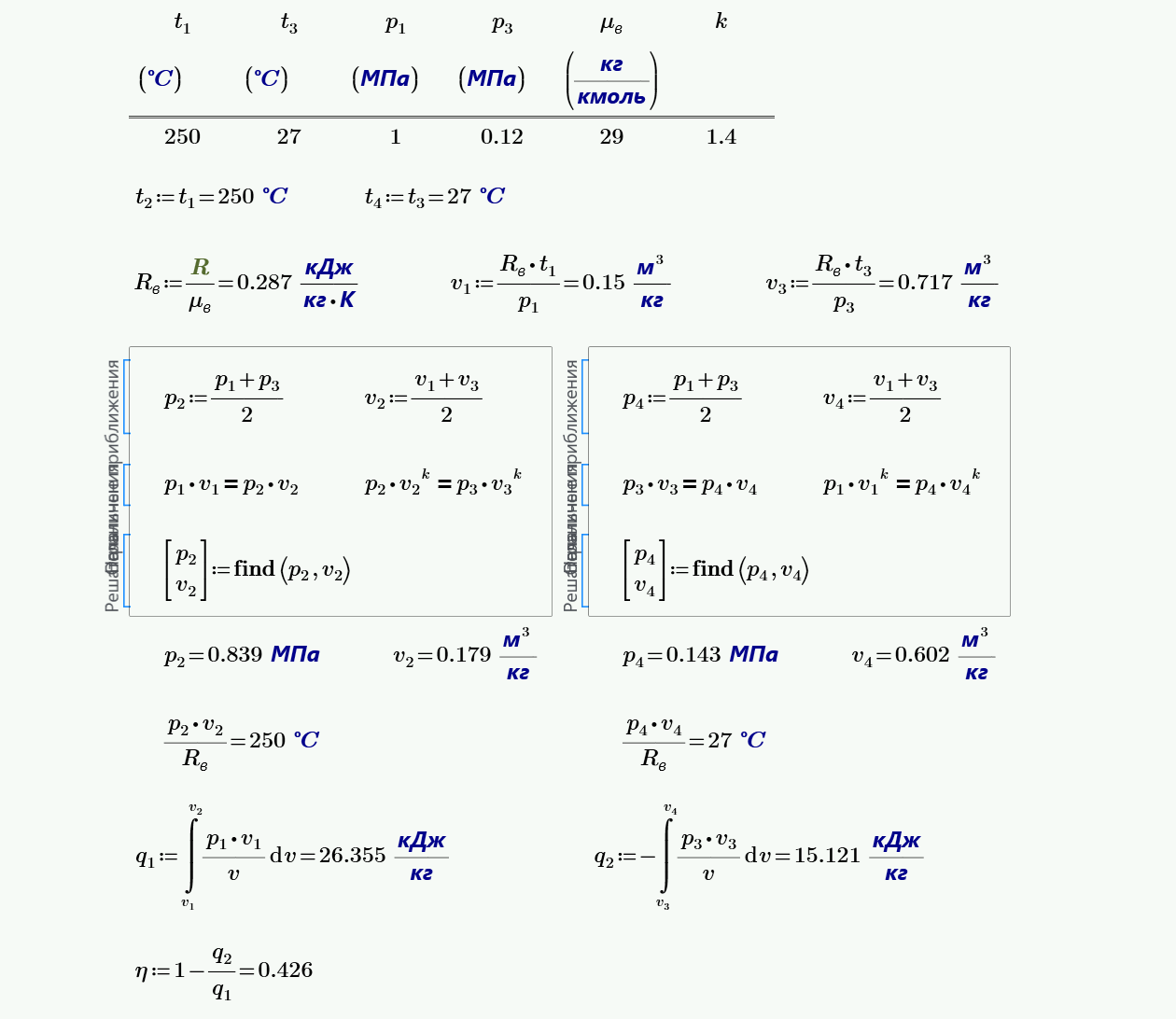
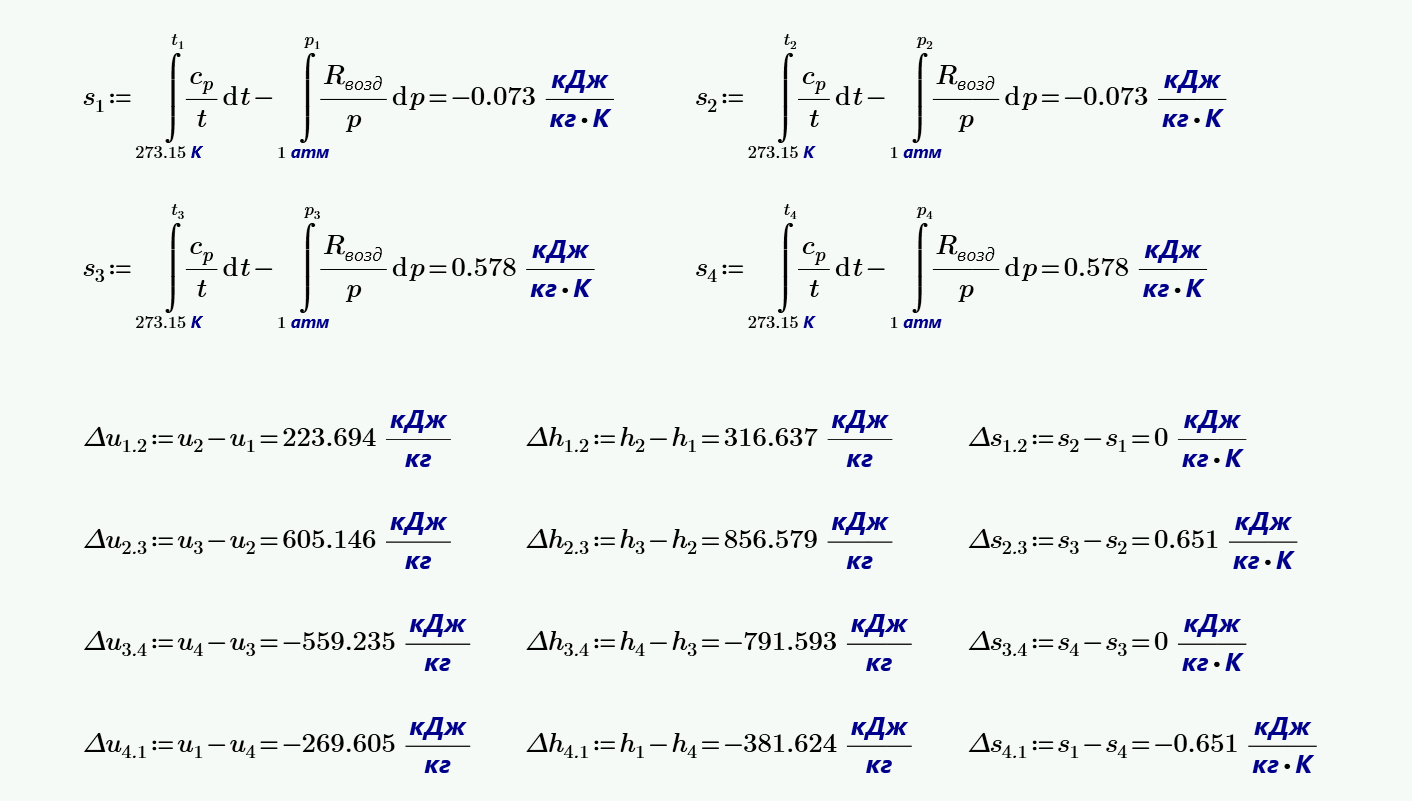
3. $1$ кг воздуха совершает цикл Карно в пределах температур $t_1=620$ °С и $t_2=27$ °С, причем наивысшее давление составляет $6$ МПа, а наинизшее $0.1$ МПа. Определить параметры состояния воздуха в характерных точках цикла, работу, термический КПД цикла, а также количество подведенной и отведенной теплоты.
4. $1$ кг воздуха совершает цикл Карно в пределах температур $t_1=250$ °С и $t_2=27$ °С, причем наивысшее давление составляет $1$ МПа, а наинизшее $0.12$ МПа. Определить параметры состояния воздуха в характерных точках цикла, работу, термический КПД цикла, а также количество подведенной и отведенной теплоты.
5. Исходными данными для выполнения расчетов служат:
- схема цикла Отто;
- степень сжатия $\varepsilon$;
- степень повышения давления $\lambda$;
- температура воздуха, поступающего в цилиндры двигателя $t_1$;
- теоретическая мощность двигателя $N$;
- давление рабочего тела (воздух) в точке 1 принять равным $p_1 = 10^5$ Па;
- Теплоемкость воздуха считать не зависящей от температуры. Принять: $c_p = 1.005$ кДж/кг·К, $c_v = 0.71$ кДж/кг·К.
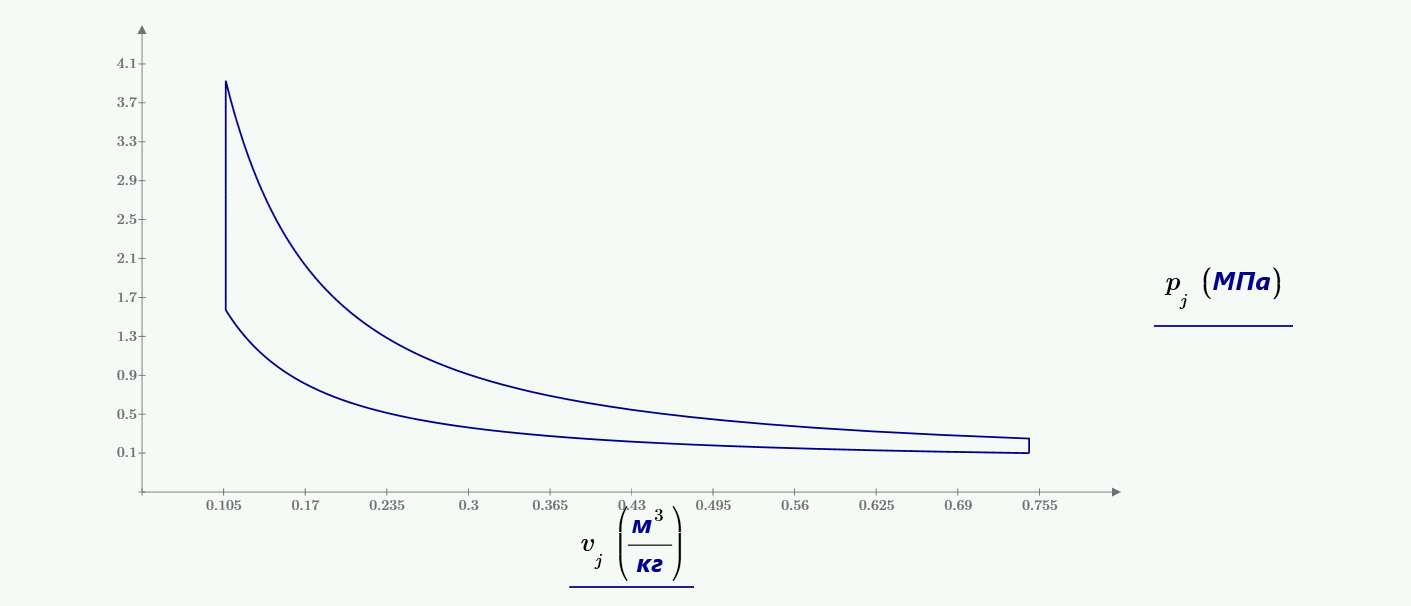
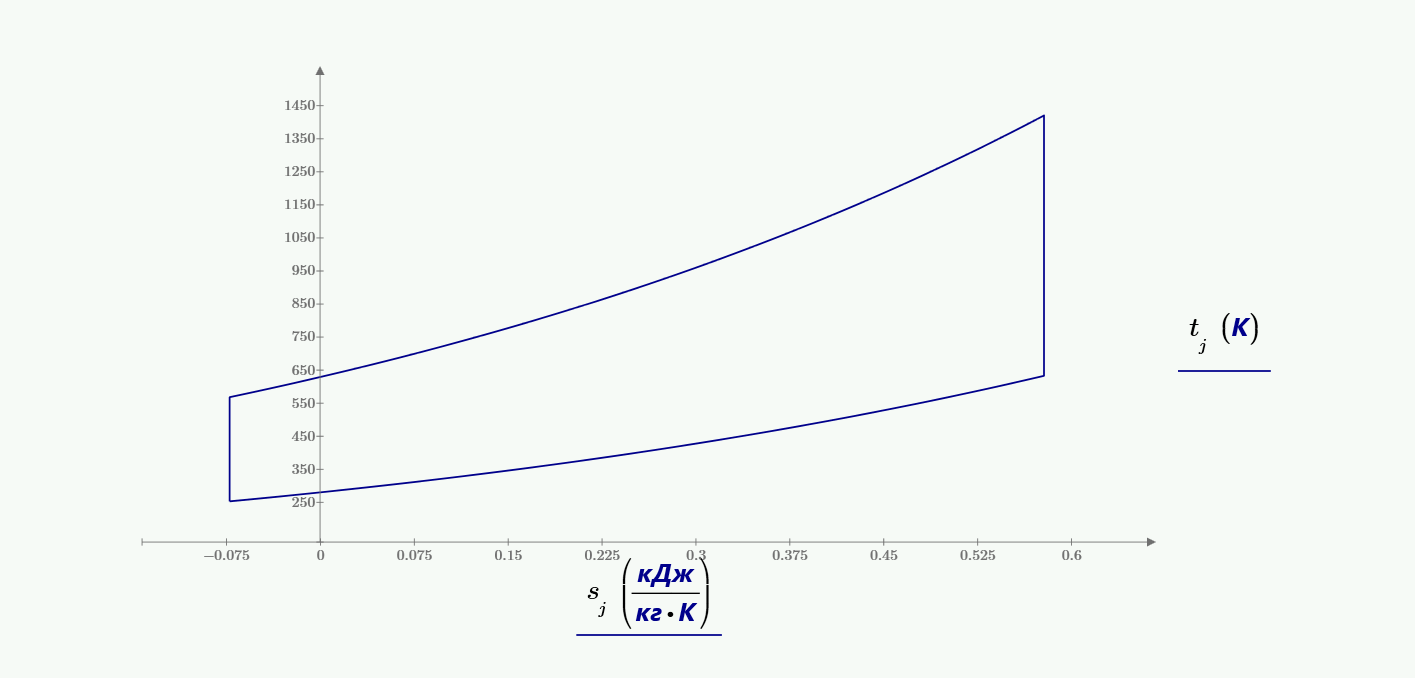
Требуется рассчитать параметры рабочего тела $Р$, $v$, $T$, $u$, $h$ для узловых точек заданногo цикла. Построить цикл в масштабе в координатах $P-v$ и $T-s$. Определить подведенное тепло, отведенное тепло и работу цикла. Рассчитать термический коэффициент полезного действия цикла.
6. Температура воспламенения топлива, подаваемоего в циллиндр двигателя с изобарным подводом теплоты, равна $800$ °С. Определить минимально необходимое значение степени сжатия, если начальная температура воздуха $t_1=77$ °С. Сжатие считать адиабатным.
7. Для идеального цикла газовой турбины с подводом теплоты при $p=const$ найти параметры в характерных точках, полезную работу, термический КПД, количество подведенной и отведенной теплоты, если дано: $p_1=100$ кПа, $t_1=27$ °C, $t_3=700$ °C, $λ=\frac
8. Для идеального цикла газовой турбины с подводом теплоты при p=const найти параметры в характерных точках, полезную работу, термический КПД, количество подведенной и отведенной теплоты, если дано: $p_1=0.1$ МПа, $t_1=17$ °C, $t_3=600$ °C, $λ=\frac
9. Газотурбинная установка работает с подводом теплоты v=const и с полной регенерацией. Известны параметры: $t_1=30$ °C и $t_5=400$ °C, а также $λ=\frac
10. Газотурбинная установка работает с подводом теплоты $p=const$ и с полной регенерацией. Известны параметры: $t_1=30$ °C и $t_5=800$ °C, а также $λ=\frac
Администратор сайта: Колосов Михаил
email:
Copyright © 2011-2021. All rights reserved.
Физика
Круговой процесс (цикл) всегда состоит из нескольких процессов, в том числе и изопроцессов.
Согласно первому началу термодинамики, в каждом из таких процессов газом может совершаться работа и может изменяться его внутренняя энергия. Теплота, полученная или отданная газом в каждом процессе, будет различной.
В таблице отражены расчетные формулы, условные обозначения и нулевые значения для работы, изменения внутренней энергии и теплоты, полученной газом в некоторых процессах.
Работа, совершенная газом, A
Изменение внутренней энергии газа, Δ U
Количество теплоты, полученной газом, Q = A + Δ U
При решении задач на вычисление коэффициента полезного действия произвольного цикла следует использовать следующий алгоритм :
1) построить график кругового процесса в координатах p ( V );
2) выделить участки, соответствующие изопроцессам;
3) заполнить таблицу:
4) проанализировать, положительным или отрицательным является выражение для теплоты, полученной/отданной газом, в каждом процессе (в последней колонке таблицы указать соответствующий знак):
- газ получает теплоту, если Q > 0;
- газ отдает теплоту, если Q < 0;
5) рассчитать работу газа за цикл, суммируя алгебраически работы газа на каждом из участков (т.е. складывая значения работ из третьей колонки таблицы с учетом соответствующего знака):
A = A 12 + A 23 + . + A n1 ;
6) найти теплоту, полученную газом за цикл Q получ , суммируя только те значения Q , которые являются положительными;
7) рассчитать коэффициент полезного действия для рассмотренного цикла по формуле
η = A Q получ ⋅ 100 % .
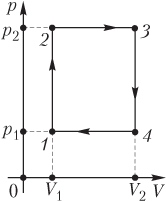
Пример 12. Идеальный одноатомный газ в идеальной тепловой машине совершает циклический процесс, состоящий из двух изохор и двух изобар. Максимальное давление газа в 4,00 раза больше минимального. Максимальный объем газа в 6,00 раз больше минимального. Определить коэффициент полезного действия идеальной тепловой машины.
Решение . На рисунке
изображен циклический процесс, происходящий с определенной массой идеального одноатомного газа, в координатах p ( V ). Процесс состоит из двух изохор и двух изобар:
1 – 2 — изохора ( V 1 = const);
2 – 3 — изобара ( p 2 = const);
3 – 4 — изохора ( V 2 = const);
4 – 1 — изобара ( p 1 = const).
Коэффициент полезного действия цикла 1 – 2 – 3 – 4 – 1 , изображенного на рисунке, определяется формулой
η = A 1 2 + A 2 3 + A 3 4 + A 4 1 Q получ ⋅ 100 % ,
где A 12 — работа, совершаемая газом на участке 1 – 2 ; A 23 — работа, совершаемая газом на участке 2 – 3 ; A 34 — работа, совершаемая газом на участке 3 – 4 ; A 41 — работа, совершаемая газом на участке 4 – 1 ; Q получ — количество теплоты, полученной газом за цикл.
Запишем первое начало термодинамики для каждого участка:
- участок 1–2 (изохора) —
Q 12 = A 12 + ∆ U 12 ,
где A 12 — работа газа при изохорном процессе на участке 1 – 2 , A 12 = 0; Δ U 12 — изменение внутренней энергии газа на участке 1 – 2 , ∆ U 12 = = 1,5ν R ( T 2 − T 1 ); ν — количество вещества (газа); R — универсальная газовая постоянная; T 1 — начальная температура газа на участке 1 – 2 ; T 2 — конечная температура газа на участке 1 – 2 ;
- участок 2 – 3 (изобара) —
Q 23 = A 23 + ∆ U 23 ,
где A 23 — работа газа при изобарном процессе на участке 2 – 3 , A 23 = p 2 ( V 2 − V 1 ); p 2 — давление газа на участке 2 – 3 ; V 1 — начальный объем газа на участке 2 – 3 ; V 2 — конечный объем газа на участке 2 – 3 ; Δ U 23 — изменение внутренней энергии газа на участке 2 – 3 , ∆ U 23 = = 1,5ν R ( T 3 − T 2 ); T 2 — начальная температура газа на участке 2 – 3 ; T 3 — конечная температура газа на участке 2 – 3 ;
- участок 3 – 4 (изохора) —
Q 34 = A 34 + ∆ U 34 ,
где A 34 — работа газа при изохорном процессе на участке 3 – 4 , A 34 = 0; Δ U 34 — изменение внутренней энергии газа на участке 3 – 4 , ∆ U 34 = = 1,5ν R ( T 4 − T 3 ); T 3 — начальная температура газа на участке 3 – 4 ; T 4 — конечная температура газа на участке 3 – 4 ;
- участок 4 – 1 (изобара) —
Q 41 = A 41 + ∆ U 41 ,
где A 41 — работа газа при изобарном процессе на участке 4 – 1 , A 41 = p 1 ( V 1 − V 2 ); p 1 — давление газа на участке 4 – 1 ; V 2 — начальный объем газа на участке 4 – 1 ; V 1 — конечный объем газа на участке 4 – 1 ; Δ U 41 — изменение внутренней энергии газа на участке 4 – 1 , ∆ U 41 = = 1,5ν R ( T 1 − T 4 ); T 4 — начальная температура газа на участке 4 – 1 ; T 1 — конечная температура газа на участке 4 – 1 .
Газ получает теплоту на участках 1 – 2 и 2 – 3 , так как именно на этих участках количество теплоты является положительным. Следовательно, полученное за цикл количество теплоты определяется формулой
Q получ = Q 1 2 + Q 2 3 = 1,5 ν R ( T 2 − T 1 ) + p 2 ( V 2 − V 1 ) + 1,5 ν R ( T 3 − T 2 ) .
После преобразований получим
Q получ = p 2 ( V 2 − V 1 ) + 1,5 ν R ( T 3 − T 1 ) .
Коэффициент полезного действия цикла
η = p 2 ( V 2 − V 1 ) + p 1 ( V 1 − V 2 ) p 2 ( V 2 − V 1 ) + 1,5 ν R ( T 3 − T 1 ) ⋅ 100 % .
Запишем уравнение Менделеева — Клапейрона для состояний идеального газа, обозначенных на графике точками 1 и 3 :
p 1 V 1 = ν RT 1 , p 2 V 2 = ν RT 3 .
В выражении для коэффициента полезного действия произведем соответствующую замену, раскроем скобки и приведем подобные слагаемые:
η = p 2 V 2 − p 2 V 1 + p 1 V 1 − p 1 V 2 2,5 p 2 V 2 − p 2 V 1 − 1,5 p 1 V 1 ⋅ 100 % .
Выполним почленное деление числителя и знаменателя на произведение ( p 1 V 1 ):
η = p 2 V 2 p 1 V 1 − p 2 p 1 + 1 − V 2 V 1 2,5 p 2 V 2 p 1 V 1 − p 2 p 1 − 1,5 ⋅ 100 % .
С учетом того, что p 1 и V 1 являются минимальными значениями давления и объема газа, а p 2 и V 2 — максимальными, выполним подстановку:
p 2 = 4,00 p 1 , V 2 = 6,00 V 1 .
Искомый коэффициент полезного действия составит
η = 4,00 ⋅ 6,00 − 4,00 + 1,00 − 6,00 2,5 ⋅ 4,00 ⋅ 6,00 − 4,00 − 1,50 ⋅ 100 % = 27,5 .
Пример 13. Рабочим веществом идеальной тепловой машины является идеальный одноатомный газ. Коэффициент полезного действия цикла 1 – 2 – 3 – 1 равен 30 %, а коэффициент полезного действия цикла 1 – 3 – 4 – 1 равен 40 %. Определить коэффициент полезного действия тепловой машины, работающей по циклу 1 – 2 – 3 – 4 – 1 .
Решение . 1. Коэффициент полезного действия цикла 1 – 2 – 3 – 4 – 1 определяется формулой
η = A 1 2 + A 2 3 + A 3 4 + A 4 1 Q получ ⋅ 100 % ,
где A 12 — работа, совершаемая газом на участке 1 – 2 ; A 23 — работа, совершаемая газом на участке 2 – 3 ; A 34 — работа, совершаемая газом на участке 3 – 4 ; A 41 — работа, совершаемая газом на участке 4 – 1 ; Q получ — количество теплоты, полученной газом за цикл.
Запишем первое начало термодинамики для каждого участка:
- участок 1 – 2 —
Q 12 = A 12 + ∆ U 12 = A 12 + 1,5ν R ( T 2 − T 1 ) > 0,
где Δ U 12 — изменение внутренней энергии газа на участке 1 – 2 , ∆ U 12 = = 1,5ν R ( T 2 − T 1 ); ν — количество вещества (газа); R — универсальная газовая постоянная; T 1 — начальная температура газа на участке 1 – 2 ; T 2 — конечная температура газа на участке 1 – 2 ;
- участок 2 – 3 —
Q 23 = A 23 + ∆ U 23 = A 23 + 1,5ν R ( T 3 − T 2 ) > 0,
где Δ U 23 — изменение внутренней энергии газа на участке 2 – 3 , ∆ U 23 = = 1,5ν R ( T 3 − T 2 ); T 2 — начальная температура газа на участке 2 – 3 ; T 3 — конечная температура газа на участке 2 – 3 ;
- участок 3 – 4 —
Q 34 = A 34 + ∆ U 34 = A 34 + 1,5ν R ( T 4 − T 3 ) < 0,
где Δ U 34 — изменение внутренней энергии газа на участке 3 – 4 ; ∆ U 34 = = 1,5ν R ( T 4 − T 3 ); T 3 — начальная температура газа на участке 3 – 4 ; T 4 — конечная температура газа на участке 3 – 4 ;
- участок 4 – 1 —
Q 41 = A 41 + ∆ U 41 = A 41 + 1,5ν R ( T 1 − T 4 ) < 0,
где Δ U 41 — изменение внутренней энергии газа на участке 4 – 1 , ∆ U 41 = = 1,5ν R ( T 1 − T 4 ); T 4 — начальная температура газа на участке 4 – 1 ; T 1 — конечная температура газа на участке 4 – 1 .
Газ получает теплоту на участках 1 – 2 и 2 – 3 , так как Q 12 и Q 23 являются положительными. Следовательно, полученное за цикл количество теплоты определяется формулой
Q получ = Q 1 2 + Q 2 3 = A 1 2 + 1,5 ν R ( T 2 − T 1 ) + A 2 3 + 1,5 ν R ( T 3 − T 2 ) .
После преобразований имеем:
Q получ = A 12 + A 23 + 1,5ν R ( T 3 − T 1 ).
Коэффициент полезного действия цикла
η = A 1 2 + A 2 3 + A 3 4 + A 4 1 A 1 2 + A 2 3 + 1,5 ν R ( T 3 − T 1 ) ⋅ 100 % .
Установим связь входящих в формулу величин с коэффициентами полезного действия на участках 1 – 2 – 3 – 1 и 1 – 3 – 4 – 1 .
2. Коэффициент полезного действия тепловой машины, работающей по циклу 1–2–3–1 .
Запишем первое начало термодинамики для каждого участка:
- участок 1 – 2 —
Q 1 2 = A 1 2 + Δ U 1 2 = A 1 2 + 1,5 ν R ( T 2 − T 1 ) > 0 ;
- участок 2 – 3 —
Q 2 3 = A 2 3 + Δ U 2 3 = A 2 3 + 1,5 ν R ( T 3 − T 2 ) > 0 ;
- участок 3 – 1 —
Q 3 1 = A 3 1 + Δ U 3 1 = A 3 1 + 1,5 ν R ( T 1 − T 3 ) < 0 ,
где Δ U 31 — изменение внутренней энергии газа на участке 3 – 1 , ∆ U 31 = = 1,5ν R ( T 1 − T 3 ); T 3 — начальная температура газа на участке 3 – 1 ; T 1 — конечная температура газа на участке 3 – 1 .
Коэффициент полезного действия цикла 1–2–3–1 :
η 1 = A 1 2 + A 2 3 + A 3 1 A 1 2 + A 2 3 + 1,5 ν R ( T 3 − T 1 ) ⋅ 100 % .
3. Коэффициент полезного действия тепловой машины, работающей по циклу 1 – 3 – 4 – 1 .
Запишем первое начало термодинамики для каждого участка:
- участок 1 – 3 —
Q 1 3 = A 1 3 + Δ U 1 3 = A 1 3 + 1,5 ν R ( T 3 − T 1 ) > 0 ,
где Δ U 13 — изменение внутренней энергии газа на участке 1 – 3 , ∆ U 13 = = 1,5ν R ( T 3 − T 1 ); T 1 – начальная температура газа на участке 1 – 3 ; T 3 — конечная температура газа на участке 1 – 3 ;
- участок 3 – 4 —
Q 3 4 = A 3 4 + Δ U 3 4 = A 3 4 + 1,5 ν R ( T 4 − T 3 ) < 0 ;
- участок 4 – 1 —
Q 4 1 = A 4 1 + Δ U 4 1 = A 4 1 + 1,5 ν R ( T 1 − T 4 ) < 0 .
Коэффициент полезного действия цикла 1–3–4–1 :
η 2 = A 1 3 + A 3 4 + A 4 1 A 1 3 + 1,5 ν R ( T 3 − T 1 ) ⋅ 100 % .
Выражения для КПД образуют систему:
η = A 1 2 + A 2 3 + A 3 4 + A 4 1 A 1 2 + A 2 3 + 1,5 ν R ( T 3 − T 1 ) ⋅ 100 % , η 1 = A 1 2 + A 2 3 + A 3 1 A 1 2 + A 2 3 + 1,5 ν R ( T 3 − T 1 ) ⋅ 100 % , η 2 = A 1 3 + A 3 4 + A 4 1 A 1 3 + 1,5 ν R ( T 3 − T 1 ) ⋅ 100 % , >
которую необходимо решить относительно η.
Из второго уравнения системы следует
A 1 2 + A 2 3 = 1,5 ν R η 1 ( T 3 − T 1 ) − A 3 1 1 − η 1 ,
A 1 3 + A 3 4 = 1,5 ν R η 2 ( T 3 − T 1 ) − A 1 3 ( 1 − η 2 ) ,
где η 1 и η 2 представлены в долях.
Подставим полученные уравнения в первое уравнение системы и преобразуем выражение
η = ( η 1 + η 2 − η 1 η 2 ) ( 1,5 ν R ( T 3 − T 1 ) + A 1 3 ) ( 1,5 ν R ( T 3 − T 1 ) − A 3 1 ) ⋅ 100 % .
η = ( η 1 + η 2 − η 1 η 2 ) ⋅ 100 % .
η = ( 0,3 + 0,4 − 0,3 ⋅ 0,4 ) ⋅ 100 % = 58 % .
КПД тепловой машины, работающей по циклу 1 – 2 – 3 – 4 – 1 , составляет 58 %.
Потери энергии в дизельном двигателе. Тепловой баланс дизельного двигателя
Все потери энергии при работе дизельного двигателя можно разделить на две большие группы: механические потери и тепловые потери.
К механическим потерям в дизельных двигателях относят:
- потери мощности на трение NTP – составляют большую часть механических потерь. Эти потери вызываются трением во всех сопряженных парах деталей, главными из которых являются поршень с поршневыми кольцами и стенки цилиндра, трение в подшипниках коленчатого вала. К возрастанию механических потерь приводят: увеличение газовых сил с повышением нагрузки; инерционных сил с повышением частоты вращения; ухудшение обработки поверхностей деталей; нарушения в работе систем смазки и охлаждения;
- потери мощности на совершение насосных ходов поршня N НАС – определяются сопротивлениями впускных и выпускных клапанов. В двухтактных дизелях с щелевой бесклапанной схемой продувки эти потери отсутствуют;
- потери мощности на привод вспомогательных механизмов N ВМ –обычно включают затраты мощности на привод агрегатов, без которых невозможна нормальная работа двигателя: водяной, масляный, топливный насосы; регулятор частоты вращения; механизм газораспределения и т.д. Эти потери зависят от конструктивного исполнения ВМ, их совершенства, размеров и технического состояния;
- потери мощности на вентиляцию N ВЕНТ – учитывают затраты на преодоление трения между движущимися деталями (поршнем, шатунами, коленчатым валом) и воздухом;
- потери мощности на механический привод компрессора N К – присутствуют только в двигателях с подключенными турбокомпрессорами, приводимыми во вращение от коленчатого вала самого дизеля. Эти потери зависят от размеров и типа компрессора.
В общем случае механические потери представляют собой сумму:
К тепловым потерям в дизельных двигателях относят:
- теплоту, отводимую в охлаждающую среду–Q ОХЛ. Эта потеря состоит из суммы теплоты, отводимой в воду – Q В, и в смазочное масло–Q М. Q В и Q М зависят, в свою очередь, от разности температур масла и воды на входе – 1 t в двигатель и на выходе – 2 t из двигателя, теплоемкости жидкостей (масла – СМ , и воды – СВ ), и расхода охлаждающих сред- GМ и GВ:
Теплота, отводимая в охлаждающую среду, состоит их теплоты, отданной рабочим телом, и теплоты, эквивалентной работе трения. Теплота, израсходованная на потери трения, переходит в основном в охлаждающую жидкость: теплота трения поршня о цилиндр – в охлаждающую воду, а теплота трения подшипников – в смазочное масло. Теплоту трения не включают в тепловой баланс дизеля, кроме доли теплоты трения, не перешедшей в охлаждающую среду (учитывается остаточным членом баланса).
- теплоту с уходящими газами – QГ . Эта потеря определяется как разность энтальпий уходящих из двигателя выхлопных газов и поступающего в цилиндр свежего заряда воздуха:
- - GГ, GB – часовой расход выхлопных газов и воздуха;
- - CрГ, СрВ – изобарная теплоемкость выхлопных газов и воздуха;
- - TЗТ – температура газов за турбиной (при турбонаддуве);
- - Тв – температура воздуха на входе в цилиндр.
- неучтенные потери QНП – в эту группу относят следующие виды потерь:
- - Q Л – теплоту лучеиспускания в окружающую среду (потеря теплоты через стенки двигателя);
- - QН. СГ – теплоту, эквивалентную неполному сгоранию топлива (химический недожог топлива);
- - Q УТ – унос топлива в капельно-жидком состоянии с уходящими газами (механический недожог топлива);
- - QК. ЭН – теплоту кинетической энергии выхлопных газов.
Тепловым балансом двигателя называется распределение затраченной теплоты на полезную работу и различного рода потери. В общем виде уравнение теплового баланса дизельного двигателя имеет вид:
Дизели относятся к числу наиболее экономичных двигателей. КПД лучших образцов достигает 50 ÷ 51 %, однако и в дизелях теряется значительное количество тепловой энергии: 30 ÷ 40 % – с выхлопными газами, и 10 ÷ 20 % – с охлаждающими средами (с водой и маслом).
Потоки теплоты в ДЭУ (дизельная энергетическая установка) имеют сложный характер, обусловленный наличием нескольких видов энергии: химической энергии топлива; механической энергии, выработанной двигателем; электрической энергии, полученной во вспомогательных двигателях; тепловой энергии в виде пара, горячей воды, выхлопных газов, нагретого масла; потенциальной энергии сжатого в компрессоре воздуха и т.д.
- QT– теплота, эквивалентная химической энергии сгорания топлива;
- Qi– теплота, эквивалентная индикаторной работе;
- Qe – теплота, эквивалентная эффективной работе двигателя;
- Потери теплоты: QОХЛ – с охлаждающей средой; QГ– с уходящими (выхлопными) газами;
- QНП – неучтенные потери; QСТ – в стенки двигателя;
- QВ.П. – полные потери газа в выпускном патрубке;
- QМЕХ – механические потери; QТР – на трение поршня и колец;
- QН.СГ – от неполного сгорания топлива;
- QК.ЭН – с кинетической энергией газов;
- QЛ – с лучеиспусканием;
- QКОЛ – в охлаждающую среду из выпускного коллектора.
Графически уравнение теплового баланса и распределение потоков тепла, полученного в двигателе, можно изобразить на диаграмме теплового баланса двигателя. На рис. 26 изображена диаграмма теплового баланса для дизельного двигателя без наддува и утилизации теплоты.
Примерные значения эффективной работы и потерь энергии для различных типов современных дизельных двигателей сведены в таблицу:
Литература
Судовые энергетические установки. Дизельные и газотурбинные установки. Болдырев О.Н. [2003]
Определить количество теплоты отдаваемое каждым килограммом отработавших газов дизеля
Тепловой баланс двигателя получают на основании исследований его в различных условиях.
Уравнение теплового баланса имеет следующий вид:
Qo = Qe + QoX, + Qe + Qn.c + Qocm,(267)
общее количество теплоты, израсходованной в единицу времени приработе двигателя на заданном режиме; Qe— теплота,эквивалентнаяэффективнойработедвигателя; Qox.i— теплота, отданнаяв охлаждающую среду; Ог — теплота, унесеннаяиздвигателясотработавшими газами; QHC— неиспользованнаячастьтеплотытопливаиз-за
неполнотысгорания; Qocm— остаточныйчлен баланса,определяющий потери,не учтенныеприведеннымивышечленамиуравнения баланса теплоты. Каждую составляющую баланса можно определять в процентах от всего количества введенной теплоты. Тогда
де = 1100%; дохл = fe. 100%;дг = ^ • 100%;
<7к.с = ^Ю0%;9ост = ^Ю0%. Очевидно,что
Яе + Яохл + Яг + Ян. с + Яост = 100%(268)
Общее количествотеплоты,израсходованной втечение1ч,
Q0==HUGTкдж/ч,(269)
где GT— часовой расход топлива в кг/ч. Теплота,эквивалентная эффективной работе,
<2е = 3600 Neкдж/ч.(270)
Теплоту, передаваемую охлаждающей среде через стенки цилиндров, головку цилиндров, поршень и поршневые кольца, можно при водяном охлаждении определить по уравнению
1 ч, в кг; tebix— температуравыходящейиздвигателяводыв° С;
Теплота, унесенная с отработавшими газами,
за выпускным патрубком, в ° С; t0— температурасвежегозаряда, поступившегов цилиндр двигателя,вс С. Всистемеединиц,основаннойнакалории,формула(272) имееттотжевид,нотеплоемкостирсрицсрвыраженыв ккал/(кг -град).
Величину QHCпри а^1 обычно отдельно не подсчитывают, а включают в Qocm, который можно определить следующим образом:
Qocm = Qo-(Qe + Qe + QZ)-(273)
Если испытания проводятся при а<^1, то теплота, не использованная из-за химической неполноты сгорания,
где Л-Нщ — неиспользованная теплота сгорания, подсчитываемая поуравнению(200).
При увеличении числа оборотов до 3600 в минуту эффективно используемая теплота увеличивается с 24 до 27,5%. Количество теплоты, отданной охлаждающей воде, при увеличении числа оборотов уменьшается с 36 до 27% при заметном увеличении количества теплоты, унесенной с отработавшимигазами.
Видно, что наибольшее количество теплоты эффективно используется при а = = 1,1-ь1,15. При а = 0,85 доля не использованной теплоты из-за неполноты сгорания qH_c= 20%.
Читайте также: