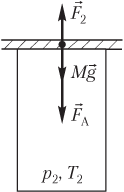Как изменится давление газа в цилиндре если поршень медленно опустить на 1 3 высоты цилиндра
Как изменится давление газа в цилиндре если поршень медленно опустить на 1 3 высоты цилиндра
В сосуде, закрытом подвижным поршнем, находятся в равновесии вода и водяной пар. Объём сосуда очень медленно уменьшают, опуская поршень из положения 1 в положение 2.
График зависимости давления в сосуде от объёма правильно показан на рисунке
Поскольку, согласно условию, водяной пар находится в состоянии теплового равновесия с водой, заключаем, что это насыщенный пар. Давление насыщенного пара зависит только от температуры. Так как поршень двигают медленно, в каждый момент успевает установиться тепловое равновесие. Роль термостата играет окружающая среда. Таким образом, описанный в задаче процесс идет изотермически, а значит, давление пара в сосуде остается неизменным (его излишки конденсируют в воду).
если процесс идет изотермический значит ответ №1?
Будьте внимательнее, в сосуде не идеальный газ, а жидкость, находящаяся в равновесии со своим паром
Если процесс изотермический, значит температура постоянная а не давление, и тогда почему 3 ответ правильный ?
Системы могут быть самые разные, поэтому не спешите применять законы, справедливые только для идеального газа. Посмотрите предыдущий комментарий и еще раз внимательно прочитайте решение.
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). В сосуд закачивается ещё такое же количество газа при неизменной температуре. Как изменится в результате этого объём газа, его давление и действующая на шарик архимедова сила?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Обьем газа | Давление газа | Архимедова сила |
В начальном и конечном состояниях поршень покоится, а значит, полная сила, действующая на него, равна нулю. Отсюда делаем вывод, что давление не изменяется ().
Для газа в сосуде выполняется уравнение состояния Клапейрона — Менделеева: Увеличение количества вещества газа при неизменных температуре и давлении приведет к увеличению объема.
Сила Архимеда определяется плотностью среды, в которую помещено тело (). Поскольку плотность газа не изменяется сила Архимеда не изменяется.
В условии задачи не сказано, что поршень покоится в начальном и конечном состоянии
Поршень будет иметь устойчивое положение равновесия. Именно об этом и идет речь в решении. А в процессе перехода из начального положения в конечное позиция поршня изменяется
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). Газ охладили. Как изменится в результате этого объём газа, его давление и действующая на шарик архимедова сила?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Обьем газа | Давление газа | Архимедова сила |
Поршень подвижный, следовательно, давление газа не изменяется и равно атмосферному. При изобарном процессе для газа выполняется закон Гей-Люссака (). Следовательно, при охлаждении объем газа уменьшится.
Сила Архимеда определяется плотностью среды, в которую помещено тело (). При сжатии плотность газа увеличивается. Таким образом, увеличивается и сила Архимеда, действующая на шар.
Воздух медленно сжимают в цилиндре под поршнем. Стенки цилиндра и поршень изготовлены из тонкого, но прочного металла. Какое из приведённых ниже уравнений точнее всего описывает процесс, происходящий при этом с воздухом под поршнем?
Воздух в цилиндре можно приближенно считать идеальным газом. Поскольку поршень опускают медленно, а стенки цилиндра не теплоизолированны, то в любой момент времени успевает установиться тепловое равновесие между газом внутри и окружающей средой. Следовательно, сжатие происходит при постоянной температуре. Согласно закону Бойля-Мариотта:
В цилиндре с тонкими, но прочными металлическими стенками, находится воздух. Придерживая цилиндр, поршень медленно поднимают вверх. Какое из приведённых ниже уравнений точнее всего описывает процесс, происходящий при этом с воздухом под поршнем?
Воздух в цилиндре можно приближенно считать идеальным газом. Поскольку поршень поднимается медленно, а стенки цилиндра не теплоизолированны, то в любой момент времени успевает установиться тепловое равновесие между газом внутри и окружающей средой. Следовательно, расширение происходит при постоянной температуре. Согласно закону Бойля — Мариотта:
Вертикальный цилиндр закрыт горизонтально расположенным поршнем массой 1 кг и площадью 0,02 м 2 , который может свободно перемещаться. Под поршнем находится 0,1 моля идеального одноатомного газа при некоторой температуре Над поршнем находится воздух при нормальном атмосферном давлении. Сначала газу сообщили количество теплоты 3 Дж, потом закрепили поршень и охладили газ до начальной температуры При этом давление газа под поршнем стало равно атмосферному. Чему равна температура ? Ответ укажите в кельвинах с точностью до десятков.
Поскольку поршень может свободно двигаться, процесс передачи тепла газу происходит при постоянном давлении:
Согласно первому началу термодинамики, переданное газу тепло идет на изменение его внутренней энергии и на работу против внешних сил:
Идеальный газ подчиняется уравнению Менделеева — Клапейрона: Следовательно, при постоянном давлении изменения объёма и температуры связаны соотношением
Температура в начальном и конечном состоянии совпадает, а значит, давление и объём в начальном и конечном состояниях связаны соотношением
Таким образом, для температуры имеем
Вертикальный цилиндр закрыт горизонтально расположенным поршнем массой 1 кг и площадью 0,02 м 2 , который может свободно перемещаться. Под поршнем находится 0,1 моль идеального одноатомного газа при некоторой температуре T0. Над поршнем находится воздух при нормальном атмосферном давлении. Сначала от газа отняли количество теплоты 100 Дж. Потом закрепили поршень и нагрели газ до начальной температуры T0. При этом давление газа под поршнем стало в 1,2 раза больше атмосферного. Чему равна температура T0? Ответ укажите в кельвинах с точностью до целых.
Поскольку поршень может свободно двигаться, процесс отдачи тепла газом происходит при постоянном давлении:
Согласно первому началу термодинамики, переданное газу тепло идёт на изменение его внутренней энергии и на работу против внешних сил (несмотря на то, что тепло отнимают от газа, его можно считать переданным, но с отрицательным знаком):
Идеальный газ подчиняется уравнению Менделеева — Клапейрона: Следовательно, изменения объёма и температуры при постоянном давлении связаны соотношением
Температура в начальном и конечно состоянии совпадает, а значит, давление и объем в начальном и конечном состояниях связаны соотношением
Таким образом, для температуры имеем
Аналоги к заданию № 5735: 5770 Все
Объем уменьшился в результате процесса, поэтому pV0=1,2pa(V0-dV)
Автор решения принял и
Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 100 см 2 на 5 отсеков содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 10 5 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 2 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Какого значения достигнет F, когда объём газа в самом правом, 5-м отсеке цилиндра уменьшится в n = 2 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
Поскольку процесс медленный, то в каждый момент времени вся система находится в равновесии, и сумма горизонтальных проекций всех сил, действующих на любую её часть, равна нулю.
Для того чтобы объём отсека № 5 уменьшался, все поршни, очевидно, должны двигаться, и при этом на каждый из них будет действовать сила трения направленная влево.
Согласно закону Бойля — Мариотта, при изотермическом процессе в пятом отсеке произведение его объёма на давление в нем должно оставаться неизменным: откуда следует, что в конце процесса при объёме давление в этом отсеке будет равно При этом на правый поршень со стороны газа в пятом отсеке будет действовать сила направленная влево.
Рассмотрим теперь систему, состоящую из всех пяти поршней и четырёх отсеков (№№ 1—4) с газом между этими поршнями. В конце процесса сжатия газа в пятом отсеке на эту систему в равновесии действуют слева направо сила и сила атмосферного давления а справа налево — 5 сил трения и сила давления газа в пятом отсеке Эти силы уравновешивают друг друга, и по второму закону Ньютона:
Самым простым и доступным для каждого водителя способом диагностики двигателя является проверка компрессии в цилиндрах.
Проводим замер компрессии
Но, с другой стороны, замер компрессии иногда выдаёт относительные результаты и полностью на них ориентироваться не следует. Это всего лишь один из методов диагностики. Один из многих.

Первым показателем того, что в двигателе низкая компрессия в одном цилиндре, как минимум, является поведение авто во время движения. Двигатель не тянет.
Кстати, цифровые параметры значений компрессии для своего двигателя вы найдёте в Инструкции по эксплуатации.
Хотя процедура замера компрессии уже описана, коротко напомним. Замер производится на прогретом до 80 градусов двигателе, при наличии исправного и заряженного аккумулятора. Для получения точных параметров вам понадобится компрессометр.

Отключаем подачу топлива, выворачиваем свечи и замеряем компрессию, как при открытой, так и при закрытой дроссельной заслонке. Естественно нужен помощник. Получаем безрадостный результат – разная компрессия в цилиндрах.
Причин этому может быть сколько угодно: начиная от качества топлива и работы топливной системы, и заканчивая (в худшем случае) неисправностью поршней, клапанов и самих цилиндров. Не забудьте добавить сюда дефекты в прокладках и уплотнителях.
Сразу же грозной тучей надвигается неприятный вопрос, — что, неужели нужно делать капитальный ремонт двигателя? Ответ пока однозначный – нет.
Показания компрессометра есть, нужно применять их на практике
В случае, если видна низкая компрессия в одном цилиндре и при этом работа двигателя на холостом ходу неустойчива, то большая вероятность износа кулачка распредвала, который управляет выпускным клапаном.

Если разная компрессия по схеме: низкая в двух соседних цилиндрах, то, скорее всего, прогорела прокладка между ними.

И, наконец, после того, как вы долили в каждый цилиндр немного моторного масла и повторили проверку компрессии, показания повысились – изношены поршневые кольца.
Методы устранения низкой компрессии двигателя
Как мы уже говорили, причин того, что наблюдается разная компрессия в цилиндрах масса. И, если следовать «умным» книгам, то нужно вскрытие, которое, как известно, покажет причину.
Но лишь одна мысль о том, что при разборке ГБЦ на вас навалится ворох проблем, приводит в ужас. И замена колец, замена «колпачков», сальников коленчатого вала. А если и зазор между поршнем и цилиндром нарушен, то расточки блока не миновать. Нет, об этом пока не торопитесь думать.

Поэтому, первой возможной причиной того, что образовалась низкая компрессия в цилиндре, специалисты рекомендуют считать залегание колец. Это когда происходит их чрезмерное коксование, и они практически прилипают к поршню. Если вариант, который описан ниже не устранит проблему разной компрессии в цилиндрах, то понадобятся радикальные методы.
Народный способ устранения залегания колец и повышения компрессии
Данный способ не является гарантией того, что изменяться показатели компрессометра. Но, он на самом деле эффективен, если разная компрессия в цилиндрах образовалась именно из-за залегания колец. Как минимум, совесть ваша будет чиста, и вы исключите затем этот пункт из диагностики.

- Приобретаем качественную жидкость для очистки клапанов. В инструкции к ней должно быть указано, что она добавляется в моторное масло.
- Сегодня вечером выкручиваем все свечи и заливаем в цилиндры по 50-70 мл. этой жидкости при помощи «груши» или шприца.
- Утром, через 12 часов прокручиваете двигатель, затем чистите свечи и регулируете зазоры, а только затем вкручиваете их на места.
- При запуске двигателя не пугайтесь качеству и количеству дыма из выхлопной системы.
- Выезжаете на дорогу для прохождения участков на повышенных скоростях. То есть задача состоит в том, чтобы дать двигателю максимальные нагрузки. Поэтому заранее продумайте где вы это будете делать. Учтите состояние дорожного покрытия, погодных условий, интенсивности движения. В идеале это делается на загородной трассе.
- Важно! Предыдущий пункт должен быть выполнен обязательно, иначе отлипшие за ночь продукты коксования попадут под клапан и тогда не миновать разборки ГБЦ.
- После пробега со скоростью в 100-120 км/час на участке в 10-20 км. вновь производите замер компрессии в цилиндрах.
Здесь существует два варианта: радость и ощущение счастья от увиденных цифр одинаковой компрессии, которая соответствует норме. Или горечь от предстоящей операции с разборкой ГБЦ и диагностики двигателя. Третьего не дано.
Удачи вам при устранении разности компрессии в цилиндрах.
Физика
Для идеального газа, находящегося в сосуде под поршнем , необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
- постоянным остается также количество вещества (газа):
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
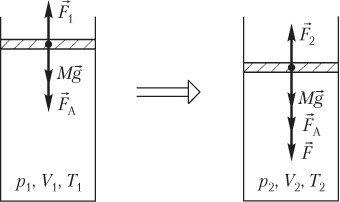
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F → (рис. 5.9).
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p 1 V 1 = ν R T 1 , p 2 V 2 = ν R T 2 , >
где p 1 , V 1 , T 1 — давление, объем и температура газа в начальном состоянии; p 2 , V 2 , T 2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
M g + F A = F 1 , M g + F A + F = F 2 , >
где M — масса поршня; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; S — площадь сечения поршня; F 1 — модуль силы давления газа на поршень в начале процесса, F 1 = p 1 S ; p 1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F 2 — модуль силы давления газа на поршень в конце процесса, F 2 = p 2 S ; p 2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
- если процесс происходит медленно, то температура газа остается постоянной –
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня , закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
- в остальных случаях поршень обладает определенной ненулевой массой —
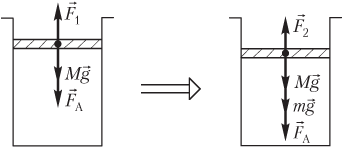
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм 2 и массой 1,80 кг находится 360 см 3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см 3 . Температура газа при его сжатии не изменяется. Определить массу гирь.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 1 , действующая со стороны газа (до его сжатия);
- сила давления газа F → 2 , действующая со стороны газа (после его сжатия);
- m g → — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
где F 1 — модуль силы давления газа, F 1 = p 1 S ; p 1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F 2 = Mg + F A + mg ,
где F 2 — модуль силы давления газа, F 2 = p 2 S ; p 2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
где V 1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
где V 2 — объем сжатого поршнем газа.
p 1 V 1 = p 2 V 2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p 1 S = M g + p A S , p 2 S = M g + p A S + m g , p 1 V 1 = p 2 V 2 , >
которую требуется решить относительно массы гирь m .
Для этого выразим отношение давлений p 2 / p 1 из первой пары уравнений:
p 2 p 1 = M g + p A S + m g M g + p A S
и из третьего уравнения:
p 2 p 1 = V 1 V 2 ,
запишем равенство правых частей полученных отношений:
M g + p A S + m g M g + p A S = V 1 V 2 .
Отсюда следует, что искомая масса определяется формулой
m = ( M + p A S g ) ( V 1 V 2 − 1 ) .
Вычисление дает результат:
m = ( 1,80 + 100 ⋅ 10 3 ⋅ 250 ⋅ 10 − 6 10 ) ( 360 ⋅ 10 − 6 240 ⋅ 10 − 6 − 1 ) = 2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см 2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение . На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 2 , действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
где F 2 — модуль силы давления нагретого газа, F 2 = p 2 S ; p 2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
где p 1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p 1 = p A ; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
где p 2 — давление нагретого газа; T 2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
p A V = ν R T 1 , p 2 V = ν R T 2 , p 2 S = M g + p A S ; >
систему необходимо решить относительно температуры T 2 , до которой следует нагреть газ.
Для этого делением первой пары уравнений
p A V p 2 V = ν R T 1 ν R T 2
получим выражение для давления нагретого газа:
p 2 = p A T 2 T 1
и подставим его в третье уравнение системы:
p A T 2 S T 1 = M g + p A S .
Преобразуем полученное выражение к виду
T 2 = T 1 ( M g + p A S ) p A S = T 1 ( M g p A S + 1 ) ,
а затем найдем разность
Δ T = T 2 − T 1 = M g T 1 p A S .
Δ T = 1,2 ⋅ 10 ⋅ 300 100 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 36 К = 36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см 2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → , действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a → :
F → + F → A + M g → = m a → ,
или в проекции на вертикальную ось —
где F — модуль силы давления газа под поршнем, F = pS ; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a = F − F A − M g M = ( p − p A ) S M − g .
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
и подставим в записанную формулу выражение для модуля ускорения:
v = 2 l ( ( p − p A ) S M − g ) .
v = 2 ⋅ 3,75 ( ( 450 − 100 ) ⋅ 10 3 ⋅ 50 ⋅ 10 − 4 75,0 − 10 ) ≈ 10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Читайте также: