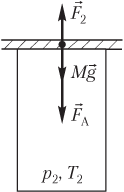Идеальный газ находится в цилиндре
Физика
Для идеального газа, находящегося в сосуде под поршнем , необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
- постоянным остается также количество вещества (газа):
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
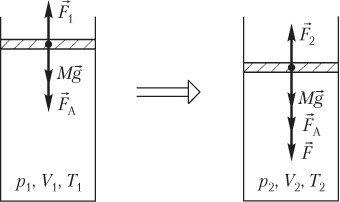
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F → (рис. 5.9).
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p 1 V 1 = ν R T 1 , p 2 V 2 = ν R T 2 , >
где p 1 , V 1 , T 1 — давление, объем и температура газа в начальном состоянии; p 2 , V 2 , T 2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
M g + F A = F 1 , M g + F A + F = F 2 , >
где M — масса поршня; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; S — площадь сечения поршня; F 1 — модуль силы давления газа на поршень в начале процесса, F 1 = p 1 S ; p 1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F 2 — модуль силы давления газа на поршень в конце процесса, F 2 = p 2 S ; p 2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
- если процесс происходит медленно, то температура газа остается постоянной –
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня , закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
- в остальных случаях поршень обладает определенной ненулевой массой —
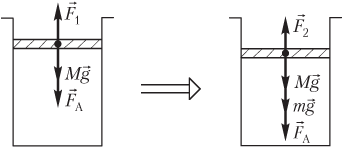
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм 2 и массой 1,80 кг находится 360 см 3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см 3 . Температура газа при его сжатии не изменяется. Определить массу гирь.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 1 , действующая со стороны газа (до его сжатия);
- сила давления газа F → 2 , действующая со стороны газа (после его сжатия);
- m g → — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
где F 1 — модуль силы давления газа, F 1 = p 1 S ; p 1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F 2 = Mg + F A + mg ,
где F 2 — модуль силы давления газа, F 2 = p 2 S ; p 2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
где V 1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
где V 2 — объем сжатого поршнем газа.
p 1 V 1 = p 2 V 2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p 1 S = M g + p A S , p 2 S = M g + p A S + m g , p 1 V 1 = p 2 V 2 , >
которую требуется решить относительно массы гирь m .
Для этого выразим отношение давлений p 2 / p 1 из первой пары уравнений:
p 2 p 1 = M g + p A S + m g M g + p A S
и из третьего уравнения:
p 2 p 1 = V 1 V 2 ,
запишем равенство правых частей полученных отношений:
M g + p A S + m g M g + p A S = V 1 V 2 .
Отсюда следует, что искомая масса определяется формулой
m = ( M + p A S g ) ( V 1 V 2 − 1 ) .
Вычисление дает результат:
m = ( 1,80 + 100 ⋅ 10 3 ⋅ 250 ⋅ 10 − 6 10 ) ( 360 ⋅ 10 − 6 240 ⋅ 10 − 6 − 1 ) = 2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см 2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение . На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 2 , действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
где F 2 — модуль силы давления нагретого газа, F 2 = p 2 S ; p 2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
где p 1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p 1 = p A ; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
где p 2 — давление нагретого газа; T 2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
p A V = ν R T 1 , p 2 V = ν R T 2 , p 2 S = M g + p A S ; >
систему необходимо решить относительно температуры T 2 , до которой следует нагреть газ.
Для этого делением первой пары уравнений
p A V p 2 V = ν R T 1 ν R T 2
получим выражение для давления нагретого газа:
p 2 = p A T 2 T 1
и подставим его в третье уравнение системы:
p A T 2 S T 1 = M g + p A S .
Преобразуем полученное выражение к виду
T 2 = T 1 ( M g + p A S ) p A S = T 1 ( M g p A S + 1 ) ,
а затем найдем разность
Δ T = T 2 − T 1 = M g T 1 p A S .
Δ T = 1,2 ⋅ 10 ⋅ 300 100 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 36 К = 36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см 2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → , действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a → :
F → + F → A + M g → = m a → ,
или в проекции на вертикальную ось —
где F — модуль силы давления газа под поршнем, F = pS ; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a = F − F A − M g M = ( p − p A ) S M − g .
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
и подставим в записанную формулу выражение для модуля ускорения:
v = 2 l ( ( p − p A ) S M − g ) .
v = 2 ⋅ 3,75 ( ( 450 − 100 ) ⋅ 10 3 ⋅ 50 ⋅ 10 − 4 75,0 − 10 ) ≈ 10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Идеальный газ находится в цилиндре
С1-1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-3. В цилиндре, закрытом подвижным поршнем, находится газ, который может просачиваться сквозь зазор вокруг поршня. В опыте по изотермическому сжатию газа его объем уменьшился вдвое, а давление газа упало в 3 раза. Во сколько раз изменилась внутренняя энергия газа в цилиндре? (Газ считать идеальным.)
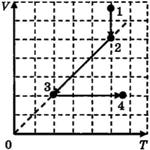
C1-5. Ha V T-диаграмме показано, как изменялись объём и температура некоторого постоянного количества разреженного газа при его переходе из начального состояния 1 в состояние 4. Как изменялось давление газа р на каждом из трёх участков 1—2, 2—3, 3—4: увеличивалось, уменьшалось или же оставалось неизменным? Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.
C1-6. В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают выдвигать из сосуда. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
С3-9. Нагреваемый при постоянном давлении идеальный одноатомный газ совершил работу 400 Дж. Какое количество теплоты было передано газу?
С3-11. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 8 раз, давление воздуха в сосуде увеличилось в 2 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)
С3-12. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 4 раза, давление воздуха в сосуде увеличилось тоже в 4 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)
С3-13. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔT. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на ΔT. Каким было изменение температуры ΔT в опытах? Масса азота m = 1 кг.
С3-14. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на 1 К. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на 1 К. Определите массу азота в опытах.
С3-15. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление p = 4 • 10 5 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газа поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3•10 3 H. Какое количество теплоты получил газ в этом процессе? Считать, что сосуд находится в вакууме.
С3-16. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 10 5 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты │Q│ = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня? Количество вещества газа постоянно.
С3-17. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа р1 = 4 · 10 5 Па. Расстояние от дна сосуда до поршня равно L. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтp = 3 · 10 3 Н. Найдите L. Считать, что сосуд находится в вакууме.
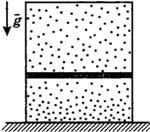
С3-18.Вертикальный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.
С3-19.В вертикальном теплоизолированном цилиндрическом сосуде под поршнем находится 0,5 моль гелия, нагретого до некоторой температуры. Поршень сначала удерживают, затем отпускают, и он начинает подниматься. Масса поршня 1 кг. Какую скорость приобретет поршень к моменту, когда поршень поднимется на 4 см, а гелий охладится на 20 К? Трением и теплообменом с поршнем пренебречь.
С3-20. Теплоизолированный сосуд объемом V = 2 м 3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль Не, а в другой — такое же количество моль А r . Температура гелия Т1 = 300 К, а температура аргона Т2 = 600 К. Определите парциальное давление аргона в сосуде после удаления перегородки.
Термодинамика С3-21. На рисунке изображено изменение состояния 1 моль идеального одноатомного газа. Начальная температура газа 27° С. Какое количество теплоты сообщено газу в этом процессе?
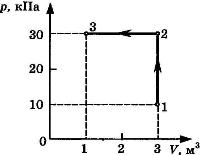
С3-23. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-24. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-25. На диаграмме (см. рисунок) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
Хочу учиться на ВМК!
Выберем в качестве начала отсчета времени момент, когда тело, смещенное от положения равновесия на расстояние x0, отпускают без начальной скорости. Тогда его координата будет меняться со временем в соответствии с выражением
где w – круговая частота колебаний, связанная с периодом колебаний соотношением . Обозначив через t0 время, за которое тело проходит от крайнего положения путь x0/2, можно записать: откуда .
Средняя скорость тела за время t0 определяется выражением:
- Два маленьких тела начинают одновременно соскальзывать без начальной скорости из точки А: первое – по внутренней поверхности гладкой сферы до ее нижней точки В, второе – по гладкой наклонной плоскости АВ. Пренебрегая трением, найдите, во сколько раз k отличаются времена движения этих тел от начальной до конечной точек. Расстояние АВ намного меньше радиуса сферы.
Поскольку расстояние между точками A и B намного меньше радиуса сферы, можно считать, что тело, скользящее по гладкой сферической поверхности радиусом R, движется как математический маятник длиной R, совершающий малые колебания. Поэтому время его движения из точки A в точку B равно четверти периода колебаний маятника, т.е. .
Тело на гладкой наклонной плоскости, составляющей угол a с горизонталью, движется с ускорением a=2Rsin a . Длина наклонной плоскости совпадает с расстоянием между точками A и B, которое, как видно из рисунка, есть l=2Rsin a . Следовательно, время движения этого тела из точки A в точку B:
- В цилиндре под невесомым поршнем площадью S = 100 см 2 находится 1 моль идеального газа при температуре t1 = 100 °C. К поршню через два блока на невесомой нерастяжимой нити подвешен груз массой М = 17 кг. На какую высоту D h поднимется груз, если медленно охладить газ до температуры t2=0°C? Атмосферное давление p0=10 –5 Па, универсальная газовая постоянная R= 8,3 Дж/(моль · К), ускорение свободного падения принять g=10 м/с 2 . Трением пренебречь.
Решение
Поршень находится под действием трех сил: силы натяжения нити T и силы давления газа в сосуде pS, направленных вверх, а также силы атмосферного давления p0S, направленной вниз. Поскольку процесс охлаждения газа является медленным, можно считать, что ускорение системы равно нулю и сила натяжения нити в каждый момент времени равна весу неподвижного груза, т.е. T=Mg. Следовательно, поршень находится в равновесии при выполнении условия:
Как видно из этой формулы, давление газа p при изменении его объема постоянно. Записывая уравнение Клапейрона–Менделеева для начального и конечного состояний газа, получаем
где T1=(t1 + 273) К; T2= (t2 + 273) К; V1 и V2 – начальный и конечный объемы газа, причем V1 – V2 = D hS. Объединяя записанные соотношения, получаем ответ:
- В вертикально расположенном цилиндре находится кислород массой m=64 г, отделенный от атмосферы поршнем, который соединен с дном цилиндра пружиной жесткостью k=8,3 · 10 2 Н/м. При температуре T1=300 К поршень располагается на расстоянии h=1 м от дна цилиндра. До какой температуры T2 надо нагреть кислород, чтобы поршень расположился на высоте H=1,5 м от дна цилиндра? Универсальная газовая постоянная R=8,3 Дж/(моль · К), молярная масса кислорода M=32 г/моль.
Решение
Поскольку в условии задачи не сказано, что поршень невесом, будем полагать, что он обладает некоторой неизвестной массой, которую обозначим через M0. Ничего не говорится также про атмосферное давление, поэтому будем считать, что оно действует, и обозначим его через p0. Таким образом, на поршень действуют в общем случае четыре силы: сила тяжести M0g, сила упругости пружины kx (x – удлинение пружины) и сила атмосферного давления p0S, направленные вниз, и сила давления газа в цилиндре pS, направленная вверх. Условия равновесия поршня в начальном и конечном состояниях имеют вид:
Здесь p1 и p2 – давления газа в начальном и конечном состояниях. Вычитая из второго уравнения первое, получаем:
С другой стороны, из уравнения Клапейрона–Менделеева, записанного для начального и конечного состояний газа, следует:
Отсюда вытекает, что
Приравнивая разности давлений газа, найденные этими двумя способами, после несложных преобразований получаем ответ:
- Вертикальная цилиндрическая трубка с запаянными концами разделена на две части тонким горизонтальным поршнем, способным перемещаться вдоль нее без трения. Верхняя часть трубки заполнена неоном, а нижняя – гелием, причем массы газов одинаковы. При некоторой температуре поршень находится точно посередине трубки. После того как трубку нагрели, поршень переместился вверх и стал делить объем трубки в отношении 1 : 3. Определите, во сколько раз a возросла абсолютная температура газов. Молярная масса неона MNe = 20 г/моль, молярная масса гелия MHe = 4 г/моль.
Обозначим через p1 и p2 давления газов, находящихся в верхней и нижней частях трубки соответственно. Поскольку количества газов в верхней и нижней частях трубки, по условию задачи, различны, а при одной и той же начальной температуре объемы этих частей одинаковы, равновесие поршня возможно только при условии, что он имеет некоторую конечную массу. Обозначив массу поршня через M0, а его площадь через S, запишем условие равновесия поршня в виде:
Используя уравнение Клапейрона–Менделеева для описания состояния гелия и неона при произвольной температуре T, получаем для разности их давлений следующее выражение:
где m – масса каждого из газов, R – универсальная газовая постоянная.
Обозначим через V объем всей трубки. Тогда начальные объемы газов (при температуре T'):
В цилиндре под поршнем находится идеальный одноатомный газ?
В цилиндре под поршнем находится идеальный одноатомный газ.
Формулы А и Б позволяют расчитать значения физических величин , характеризующие состояние газа.
Использованы обозначения : p - давление, V - объём, Е - средняя кинетическая энергия молекул, v - количество вещества.
Установите соответствие между формулами и физическими величинами, значение которых можно вычислить по этим формулам.
А. 3 / 2 * (pV / NaE) 1)Давление
2 / 3 * (vNaE / p) 2)Объём 3)Средняя кинетическая энергия молекул 4)Количество вещества.
Если можно, то объясните пожалуйста как сделать это задание.
p * V = v * Na * (2 / 3) * E отсюда и находим = = = = = = = = = = = = = = = = = =.
Каким физическим параметром характеризуется вырывание электронов из вещества А) работой выхода Б) кинетической энергией В) энергией порции света?
Каким физическим параметром характеризуется вырывание электронов из вещества А) работой выхода Б) кинетической энергией В) энергией порции света.
1. Установите соответствие между физическими величинами и единицами измерения?
1. Установите соответствие между физическими величинами и единицами измерения.
2. Установите соответствие между физическими величинами и расчетными формулами.
Гелий находится при температуре 27 С?
Гелий находится при температуре 27 С.
Средняя кинетическая энергия хаотического теплового движения всех молекул газа равна 10дж.
Подсчитайте число молекул гелия.
При какой температуре находится одноатомный газ, если средняя кинетическая энергия его равна 0, 8 * 10 ^ - 19 Дж?
При какой температуре находится одноатомный газ, если средняя кинетическая энергия его равна 0, 8 * 10 ^ - 19 Дж.
Средняя кинетическая энергия поступательногл движения молекул идеального газа равна 6 * 10 ^ - 10дж?
Средняя кинетическая энергия поступательногл движения молекул идеального газа равна 6 * 10 ^ - 10дж.
Определите концентрацию молекул газа, если он находится в сосуде под давлением 200 кПА.
1. Масса молекулы первого идеального газа в 4 раза больше массы молекулы второго газа, а температуры обоих газов одинаковы?
1. Масса молекулы первого идеального газа в 4 раза больше массы молекулы второго газа, а температуры обоих газов одинаковы.
Во сколько раз средняя квадратичная скорость молекул второго газа больше, чем первого?
2. Чему равна средняя кинетическая энергия хаотического поступательного движения молекул идеального газа при температуре 27 градусов Цельсия?
Найти число молекул в 1м ^ 3 и среднюю кинетическую энергию поступательного движения одной молекулы газа, находящегося при давлении 0?
Найти число молекул в 1м ^ 3 и среднюю кинетическую энергию поступательного движения одной молекулы газа, находящегося при давлении 0.
2 МПа и температуре 127 С.
Если можно то с "дано" пожалуйста.
Определите среднию кенетическую энергию молекул одноатомного газа и концентрации молекул при температуре 290К и давлении 0, 8МПа?
Определите среднию кенетическую энергию молекул одноатомного газа и концентрации молекул при температуре 290К и давлении 0, 8МПа.
При нагревании идеального газа его абсолютная температура увеличилась в 3 раза , как при этом изменилась средняя кинетическая энергия его молекул?
При нагревании идеального газа его абсолютная температура увеличилась в 3 раза , как при этом изменилась средняя кинетическая энергия его молекул?
При какой температуре средняя кинетическая энергия теплового движения молекул идеального газа равна кинетической энергии, которую приобретает монета достоинством в 1 коп?
При какой температуре средняя кинетическая энергия теплового движения молекул идеального газа равна кинетической энергии, которую приобретает монета достоинством в 1 коп.
Падающая с высоты 1м?
Физическая величина являющаяся мерой средней кинетической энергии молекул тела?
Физическая величина являющаяся мерой средней кинетической энергии молекул тела.
Вопрос В цилиндре под поршнем находится идеальный одноатомный газ?, расположенный на этой странице сайта, относится к категории Физика и соответствует программе для 10 - 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
Работа электрического поля по перемещению электрона А = eU , по теореме о кинетической энергии А = ΔЕ к = mv² v = √A / m = √eU / m v = √1, 6 * 10⁻¹⁹ * 4, 1 / 9, 1 * 10⁻³¹ = √0, 86 * 10¹² = 9, 3 * 10⁶м / с.
Период равен 1 : 250 = 0, 004.
Период T = 1 / v Частота v = 1 / T v = 1 / 250 = 0, 004 = 4мс Ответ 4мс.
Основной двигатель приводит в действие насосы, которые создают избыточное давление масла в гидроцилиндрах, и при этом вытягивается стрела. Водитель в кабине с помощью рычагов управляет движениями ковша и щита.
Если отрицательными станут оба тела, то оттолкнутся. Если станет одно положительным, то притянутся. Ответ : в.
Расстояние : S = 1440 км Скорость V = 90 км / ч Время движения : t1 = S / V = 1440 / 90 = 16 часов Время отдыха t2 = 8 часов Общее время в пути : t = t1 + t2 = 16 + 8 = 24 часа Средняя путевая скорость Vcp = S / t = 1440 / 24 = 60 км / ч.
Есть три больших родственных научных направления в теоретической и прикладной физике : Гидравлика, Гидродинамика и Аэродинамика. Гидравлика описывает поведение движущихся жидкостей и газов в замкнутых или как - то иначе ограниченных условиях : в тру..
Еденица массы в си это кг.
1) m * a = F - m * g * sina - u * m8g * cosa F = m * (a + g * sina + u * g * cosa) = 900 * (1 + 10 * 0, 34 + 0, 1 * 10 * 0, 94) = 4806 H P1 * V * M = m * R * T1 P2 * V * M = 0, 5 * m * R * T2 P1 / P2 = T1 / 0, 5 * T2 P2 = P1 * 0, 5 * T2 / T1 = 4 * 10..
В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ
В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ. Расстояния от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего одинаковы и равны h (рис.). Давление воздуха под верхним поршнем вдвое больше атмосферного. Вся система находится в равновесии. На верхний поршень надавливают так, что он опускается на место нижнего, сжимая газ. Каким станет расстояние х от нижнего поршня до дна сосуда? Атмосферное давление постоянно.

Обозначим h расстояние от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего, х — расстояние х от нижнего поршня до дна сосуда после сжатия, ратм — атмосферное давление, р1 — давление газа под верхним поршнем, рп — давление поршня, V1 — объем воздуха под верхним поршнем вначале, S — площадь основания поршней и дна цилиндра, р2 — давление под верхним поршнем после опускания верхнего поршня на место нижнего, рс — давление силы, придавившей поршень, V2 — новый объем воздуха под верхним поршнем, р3 — давление газа под нижним поршнем до опускания верхнего, р4 — давление газа под нижним поршнем после его сжатия, Т3 — объем воздуха под нижнем поршнем после сжатия.

Закон Бойля — Мариотта применительно к газу подверхним поршнем будет выглядеть так:
Давление газа под верхним поршнем р1 при равновесии равно сумме атмосферного давления ратм и давления поршня рп:
Но по условию задачи р1 = 2ратм, поэтому 2ратм = ратм + рп, откуда
Объем воздуха под верхним поршнем вначале был равен:
После опускания верхнего поршня на место нижнего газ под ними сжался и давление под верхним поршнем стало р2. Теперь оно равно сумме давлений атмосферы ратм, поршня рп и некоторой силы, придавившей поршень, рс:

Теперь нам предстоит решить систему уравнений (6) и (11) относительно искомого расстояния х, исключив из них неизвестные давления. Давайте в этих уравнениях сначала раскроем скобки и сделаем приведение подобных членов — может, мы их при этом немного упростим. Начнем с уравнения (6)
УРАВНЕНИЕ СОСТОЯНИЯ ГАЗА, ПРОЦЕССЫ. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ТЕПЛОЕМКОСТЬ
1.7.1.Найти максимально возможную температуру идеального газа в каждом из нижеследующих процессов:
a) ; б) , где , и - положительные постоянные, V - объем моля газа.
1.7.2.Определить наименьшее возможное давление идеального газа в процессе, происходящем по закону , где и — положительные постоянные, V — объем моля газа. Изобразить примерный график этого процесса в параметрах p, V.
1.7.3.Идеальный газ с молярной массой M находится в однородном поле тяжести, ускорение свободного падения в котором равно g. Найти давление газа как функцию высоты h, если при h = 0 давление p = p0, а температура изменяется с высотой как
a) ; б) ,
где - положительная постоянная.
1.7.4.Два теплоизолированных баллона 1 и 2 наполнены воздухом и соединены короткой трубкой с вентилем. Известны объемы баллонов, а также давление и температура воздуха в них ( , , и , ). Найти температуру и давление воздуха, которые установятся после открытия вентиля.
1.7.5.Два моля идеального газа при температуре T0 = 300 К охладили изохорически, вследствие чего его давление уменьшилось в n =2,0 раза. Затем газ изобарически расширили так, что в конечном состоянии его температура стала равной первоначальной. Найти количество тепла, поглощенного газом в данном процессе.
1.7.6.В вертикальном цилиндре под невесомым поршнем находится один моль некоторого идеального газа при температуре T. Пространство над поршнем сообщается с атмосферой. Какую работу необходимо совершить, чтобы, медленно поднимая поршень, изотермически увеличить объем газа под ним в n раз? Трения нет.
1.7.7.Внутри закрытого с обоих концов горизонтального цилиндра находится легкоподвижный поршень. Первоначально поршень делит цилиндр на две равные части, каждая объемом V0, в которых находится идеальный газ одинаковой температуры и под одним и тем же давлением p0. Какую работу необходимо совершить, чтобы, медленно двигая поршень, изотермически увеличить объем одной части газа в раз по сравнению с объемом другой части?
1.7.8.Некоторую массу азота сжали в раз (по объему) один раз адиабатически, другой раз изотермически. Начальное состояние газа в обоих случаях одинаково. Найти отношение соответствующих работ, затраченных на сжатие.
1.7.11.При некотором политропическом процессе объем аргона был увеличен в = 4,0 раза. Давление при этом уменьшилось в = 8,0 раз. Найти молярную теплоемкость аргона в этом процессе, считая газ идеальным.
1.7.12.Идеальный газ с показателем адиабаты у расширили по закону , где — постоянная. Первоначальный объем газа V0. В результате расширения объем увеличился в раз.
а) приращение внутренней энергии газа;
б) работу, совершенную газом;
в) молярную теплоемкость газа в этом процессе.
а) молярную теплоемкость газа в этом процессе;
б) уравнение процесса в параметрах T, V.
а) работу, которую произведет газ, если его температура испытает приращение ;
б) молярную теплоемкость газа в этом процессе; при каком значении а теплоемкость будет отрицательной?
а) работу, которую произведет газ, чтобы внутренняя энергия испытала приращение ;
б) молярную теплоемкость газа в этом процессе.

1.7.16.Один моль идеального газа с известным значением CV находится в левой половине цилиндра. Справа от поршня вакуум. В отсутствие газа поршень находится вплотную к левому торцу цилиндра, и пружина в этом положении не деформирована. Боковые стенки цилиндра и поршень адиабатные. Трения нет. Газ нагревают через левый торец цилиндра. Найти теплоемкость газа в этих условиях.
1.7.17.Один моль идеального газа, теплоемкость которого при постоянном давлении Cp, совершает процесс по закону , где и - постоянные. Найти:
а) теплоемкость газа как функцию его объема V;
б) сообщенное газу тепло при его расширении от V1 до V2.
1.7.18.Один моль идеального газа, теплоемкость которого при постоянном давлении Cp, совершает процесс по закону , где и - постоянные. Найти:
а) теплоемкость газа как функцию его объема V;
б) сообщенное газу тепло при его расширении от V1 до V2.
1.7.19.Найти уравнение процесса (в переменных T, V), при котором молярная теплоемкость идеального газа изменяется по закону:
а) ; б) ; в) . Здесь , и — постоянные.
а) работу, совершенную одним молем газа при его нагревании от T0 до температуры в раз большей;
Задача С6. В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ. Расстояния от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего одинаковы и равны h. Давление воздуха под верхним поршнем вдвое больше атмосферного. Вся система находится в равновесии. На верхний поршень надавливают так, что он опускается на место нижнего, сжимая газ. Каким станет расстояние х от нижнего поршня до дна сосуда? Атмосферное давление постоянно.
Задача С6. В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ. Расстояния от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего одинаковы и равны h. Давление воздуха под верхним поршнем вдвое больше атмосферного. Вся система находится в равновесии. На верхний поршень надавливают так, что он опускается на место нижнего, сжимая газ. Каким станет расстояние х от нижнего поршня до дна сосуда? Атмосферное давление постоянно.
Решение:
Поскольку об изменении температуры нам ничего не сказано, мы имеем право считать процесс сжатия газа изотермическим. Значит, здесь можно применить закон Бойля — Мариотта, записав его применительно к газу сначала под верхним поршнем, потом под нижним (рис. 181, а и б).

Закон Бойля — Мариотта применительно к газу под верхним поршнем будет выглядеть так:
Давление газа под верхним поршнем при равновесии равно сумме атмосферного давления и давления поршня :
Но по условию задачи , поэтому
Объем воздуха под верхним поршнем вначале был равен:
После опускания верхнего поршня на место нижнего газ под ними сжался и давление под верхним поршнем стало . Теперь оно равно сумме давлений атмосферы , поршня и некоторой силы, придавившей поршень, :
Новый объем воздуха под верхним поршнем станет равен:
Подставим равенства (3), (4) и (5) в формулу (1):
или после сокращения S
Теперь перейдем к газу под нижним поршнем. Запишем применительно к нему закон Бойля — Мариотта:
Давление газа под нижним поршнем до опускания верхнего было равно сумме давления газа под верхним поршнем и давления самого нижнего поршня :
согласно условию задачи и равенству (2).
Поэтому
Давление газа под нижним поршнем после его сжатия стало равно сумме давления газа под верхним поршнем и давления самого нижнего поршня :
Новый объем воздуха под нижним поршнем станет равен:
Подставим правые части равенств (8), (3), (9) и (10) в формулу (7):

Теперь нам предстоит решить систему уравнений (6) и (11) относительно искомого расстояния х, исключив из них неизвестные давления. Давайте в этих уравнениях сначала раскроем скобки и сделаем приведение подобных членов, — может, мы их при этом немного упростим. Начнем с уравнения (6):
Теперь проделаем то же самое с уравнением (11):
Если теперь разделить левые и правые части уравнений (12) и (13) друг на друга, то все неизвестные давления сократятся и мы сумеем найти расстояние х:

Отсюда .
Ответ: .
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Большая Энциклопедия Нефти и Газа
Равновесный идеальный газ находится во внешнем поле, в котором потенциальная энергия его молекул равна и ( г), температура газа Т, объем сосуда V, Около точек 1 и 2 внутри сосуда выделены элементы объема AVi и AVY Найти отношение а вероятностей hWi и Д № 2 обнаружения некоторой молекулы газа в этих элементах объема. [1]
Равновесный идеальный газ находится в однородном поле тяжести. [2]
В цилиндре под поршнем находится равновесный идеальный газ . [3]
В цилиндре под поршнем находится равновесный идеальный газ . Рассмотрим два случая: 1) газ теплоизолирован; 2) газ термостатирован. Поршень выдвигают, причем один раз - а) быстро, ( не квазистатически), другой раз - б) медленно ( квазистатически), и останавливают. После остановки поршня газ приходит в равновесное состояние. [4]
В начальный момент времени N молекул равновесного идеального газа занимают при температуре Т сферический объем радиуса R. Затем газ начинает беспрепятственно расширяться в пустоту. [5]
Эта теорема была доказана Блохом и Доминисисом [58] для частного случая равновесного идеального газа . Ранее аналогичная теорема была доказана Виком в квантовой теории поля. Существует несколько теорем, относящихся к усреднению динамических переменных по состояниям свободных частиц, и все они часто называются теоремами Вика. [6]
Таким образом, газодинамические эффекты, возникающие при гиперзвуковых течениях газа, можно разделить на две группы: первая связана с влиянием больших значений числа Маха в термодинамически равновесном идеальном газе ( основная термодинамическая модель при этом - совершенный газ с постоянными тепло-емкостями), вторая связана с проявлением внутренних свойств реальных газов при высокой температуре, не описываемых двупара-метрической моделью идеального газа. [7]
Теория констант скоростей реакций в идеальных газах подразделяется на теорию активных столкновений и теорию абсолютных скоростей реакций. В теории активных столкновений предполагается, что молекулы термодинамически равновесного идеального газа представляют собой упругие шарики. Вероятность столкновения таких шариков в единице объема в единицу времени определяется с помощью методов статистической механики. [8]
Физика
Для идеального газа, находящегося в сосуде под поршнем , необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
- постоянным остается также количество вещества (газа):
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F → (рис. 5.9).
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p 1 V 1 = ν R T 1 , p 2 V 2 = ν R T 2 , >
где p 1 , V 1 , T 1 — давление, объем и температура газа в начальном состоянии; p 2 , V 2 , T 2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
M g + F A = F 1 , M g + F A + F = F 2 , >
где M — масса поршня; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; S — площадь сечения поршня; F 1 — модуль силы давления газа на поршень в начале процесса, F 1 = p 1 S ; p 1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F 2 — модуль силы давления газа на поршень в конце процесса, F 2 = p 2 S ; p 2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
- если процесс происходит медленно, то температура газа остается постоянной –
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня , закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
- в остальных случаях поршень обладает определенной ненулевой массой —
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм 2 и массой 1,80 кг находится 360 см 3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см 3 . Температура газа при его сжатии не изменяется. Определить массу гирь.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 1 , действующая со стороны газа (до его сжатия);
- сила давления газа F → 2 , действующая со стороны газа (после его сжатия);
- m g → — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
где F 1 — модуль силы давления газа, F 1 = p 1 S ; p 1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F 2 = Mg + F A + mg ,
где F 2 — модуль силы давления газа, F 2 = p 2 S ; p 2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
где V 1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
где V 2 — объем сжатого поршнем газа.
p 1 V 1 = p 2 V 2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p 1 S = M g + p A S , p 2 S = M g + p A S + m g , p 1 V 1 = p 2 V 2 , >
которую требуется решить относительно массы гирь m .
Для этого выразим отношение давлений p 2 / p 1 из первой пары уравнений:
p 2 p 1 = M g + p A S + m g M g + p A S
и из третьего уравнения:
p 2 p 1 = V 1 V 2 ,
запишем равенство правых частей полученных отношений:
M g + p A S + m g M g + p A S = V 1 V 2 .
Отсюда следует, что искомая масса определяется формулой
m = ( M + p A S g ) ( V 1 V 2 − 1 ) .
Вычисление дает результат:
m = ( 1,80 + 100 ⋅ 10 3 ⋅ 250 ⋅ 10 − 6 10 ) ( 360 ⋅ 10 − 6 240 ⋅ 10 − 6 − 1 ) = 2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см 2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение . На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 2 , действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
где F 2 — модуль силы давления нагретого газа, F 2 = p 2 S ; p 2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
где p 1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p 1 = p A ; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
где p 2 — давление нагретого газа; T 2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
p A V = ν R T 1 , p 2 V = ν R T 2 , p 2 S = M g + p A S ; >
систему необходимо решить относительно температуры T 2 , до которой следует нагреть газ.
Для этого делением первой пары уравнений
p A V p 2 V = ν R T 1 ν R T 2
получим выражение для давления нагретого газа:
p 2 = p A T 2 T 1
и подставим его в третье уравнение системы:
p A T 2 S T 1 = M g + p A S .
Преобразуем полученное выражение к виду
T 2 = T 1 ( M g + p A S ) p A S = T 1 ( M g p A S + 1 ) ,
а затем найдем разность
Δ T = T 2 − T 1 = M g T 1 p A S .
Δ T = 1,2 ⋅ 10 ⋅ 300 100 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 36 К = 36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см 2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → , действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a → :
F → + F → A + M g → = m a → ,
или в проекции на вертикальную ось —
где F — модуль силы давления газа под поршнем, F = pS ; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a = F − F A − M g M = ( p − p A ) S M − g .
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
и подставим в записанную формулу выражение для модуля ускорения:
v = 2 l ( ( p − p A ) S M − g ) .
v = 2 ⋅ 3,75 ( ( 450 − 100 ) ⋅ 10 3 ⋅ 50 ⋅ 10 − 4 75,0 − 10 ) ≈ 10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Читайте также: