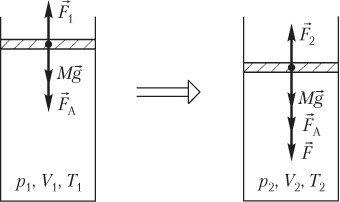
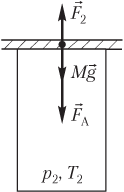Идеальный газ находится в цилиндре под поршнем поршень быстро передвигают
Физика
Для идеального газа, находящегося в сосуде под поршнем , необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
- постоянным остается также количество вещества (газа):
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
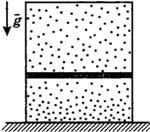
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F → (рис. 5.9).
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p 1 V 1 = ν R T 1 , p 2 V 2 = ν R T 2 , >
где p 1 , V 1 , T 1 — давление, объем и температура газа в начальном состоянии; p 2 , V 2 , T 2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
M g + F A = F 1 , M g + F A + F = F 2 , >
где M — масса поршня; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; S — площадь сечения поршня; F 1 — модуль силы давления газа на поршень в начале процесса, F 1 = p 1 S ; p 1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F 2 — модуль силы давления газа на поршень в конце процесса, F 2 = p 2 S ; p 2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
- если процесс происходит медленно, то температура газа остается постоянной –
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня , закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
- в остальных случаях поршень обладает определенной ненулевой массой —
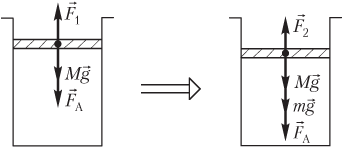
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм 2 и массой 1,80 кг находится 360 см 3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см 3 . Температура газа при его сжатии не изменяется. Определить массу гирь.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 1 , действующая со стороны газа (до его сжатия);
- сила давления газа F → 2 , действующая со стороны газа (после его сжатия);
- m g → — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
где F 1 — модуль силы давления газа, F 1 = p 1 S ; p 1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F 2 = Mg + F A + mg ,
где F 2 — модуль силы давления газа, F 2 = p 2 S ; p 2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
где V 1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
где V 2 — объем сжатого поршнем газа.
p 1 V 1 = p 2 V 2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p 1 S = M g + p A S , p 2 S = M g + p A S + m g , p 1 V 1 = p 2 V 2 , >
которую требуется решить относительно массы гирь m .
Для этого выразим отношение давлений p 2 / p 1 из первой пары уравнений:
p 2 p 1 = M g + p A S + m g M g + p A S
и из третьего уравнения:
p 2 p 1 = V 1 V 2 ,
запишем равенство правых частей полученных отношений:
M g + p A S + m g M g + p A S = V 1 V 2 .
Отсюда следует, что искомая масса определяется формулой
m = ( M + p A S g ) ( V 1 V 2 − 1 ) .
Вычисление дает результат:
m = ( 1,80 + 100 ⋅ 10 3 ⋅ 250 ⋅ 10 − 6 10 ) ( 360 ⋅ 10 − 6 240 ⋅ 10 − 6 − 1 ) = 2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см 2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение . На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 2 , действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
где F 2 — модуль силы давления нагретого газа, F 2 = p 2 S ; p 2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
где p 1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p 1 = p A ; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
где p 2 — давление нагретого газа; T 2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
p A V = ν R T 1 , p 2 V = ν R T 2 , p 2 S = M g + p A S ; >
систему необходимо решить относительно температуры T 2 , до которой следует нагреть газ.
Для этого делением первой пары уравнений
p A V p 2 V = ν R T 1 ν R T 2
получим выражение для давления нагретого газа:
p 2 = p A T 2 T 1
и подставим его в третье уравнение системы:
p A T 2 S T 1 = M g + p A S .
Преобразуем полученное выражение к виду
T 2 = T 1 ( M g + p A S ) p A S = T 1 ( M g p A S + 1 ) ,
а затем найдем разность
Δ T = T 2 − T 1 = M g T 1 p A S .
Δ T = 1,2 ⋅ 10 ⋅ 300 100 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 36 К = 36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см 2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → , действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a → :
F → + F → A + M g → = m a → ,
или в проекции на вертикальную ось —
где F — модуль силы давления газа под поршнем, F = pS ; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a = F − F A − M g M = ( p − p A ) S M − g .
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
и подставим в записанную формулу выражение для модуля ускорения:
v = 2 l ( ( p − p A ) S M − g ) .
v = 2 ⋅ 3,75 ( ( 450 − 100 ) ⋅ 10 3 ⋅ 50 ⋅ 10 − 4 75,0 − 10 ) ≈ 10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Задание 12. МКТ, термодинамика. Установление соответствия . ЕГЭ 2022 по физике

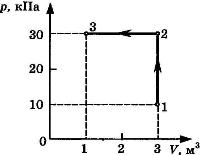
С некоторой массой идеального газа был проведён циклический процесс, изображённый на рисунке. Укажите, как менялся объём газа при переходе из 1 → 2 и 4 → 1. Для каждого случая определите соответствующий характер изменения:
| Процессы | Характер изменения |
| A) Процесс 1 → 2 Б) Процесс 4 → 1 | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждого процесса. Цифры в ответе могут повторяться.
Решение
В процессе 1-2 объем газа не менялся, т.к. переход 1-2 - это изохора, покольку его продолжение идет через начало координат. Переход 4-1 - изобара, т.к. $p_1=p_4$, тогда $
Задача 10
В сосуде объёмом V при давлении p и температуре T находится идеальный газ массой m и молярной массой M . Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физические явления | Формулы |
| А) давление газа Б) температура газа | 1) $ 2) $ 3) $ 4) $ |
Решение
Из формул и формулировок МКТ очевидно, что $P=
Задача 11
По мере понижения температуры воды от +40◦С до −20◦С она находилась сначала в жидком состоянии, затем происходил процесс её отвердевания и дальнейшее охлаждение твёрдой фазы воды–льда. Изменялась ли внутренняя энергия воды во время этих процессов и если изменялась, то как? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Отвердевание воды Б) Охлаждение льда | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
1) Отвердевание воды и охлаждение льда два процесса, подчиняющихся первому началу термодинамики, согласно которому внутренняя энергия изменяется при совершении работы или передачи тепла. Следовательно, внутренняя энергия воды уменьшилась в ходе всех двух процессов.
Задача 12
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит шарик. Из сосуда выпускается половина газа при неизменной температуре. Как изменились в результате этого объём газа и действующая на шарик архимедова сила? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Объём газа Б) Архимедова сила | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если у сосуда выпустить половину газа, то атмосферное давление уравновесит давление поршнем и поршень передвинется вниз, вследствие чего, объем газа уменьшится. Архимедова же сила, действующая на шарик, не изменится, поскольку плотность газа под поршнем останется неизменной: $F_<арх>=p_г·g·V_ш$, где $g=9.8м/с^2$ - ускорение свободного падения, $V_ш$ - объем шарика, $p_г$ - плотность газа под поршнем.
Задача 13
Температуру нагревателя тепловой машины уменьшили, оставив температуру холодильника прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и количество теплоты, отданное газом за цикл холодильнику? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) КПД тепловой машины Б) Количество теплоты, отданное газом за цикл холодильнику | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если понизить температуру нагревателя при неизменной температуре холодильника, то КПД идеальной тепловой машины уменьшается в соответствие с уравнением: $η=(1-
Задача 14
Если налить воду в открытый сосуд, то она начнёт испаряться. Как будут меняться при этом её температура и внутренняя энергия? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
При испарении, жидкость покидают наиболее быстрые молекулы, поэтому средняя скорость остальных молекул жидкости становится меньше. Следовательно, и средняя кинетическая энергия остающихся в жидкости молекул уменьшается. Это означает, что температура жидкости и внутренняя энергия испаряющейся жидкости уменьшается.
Задача 15
Ученик наблюдает за процессом кипения воды, нагреваемой в кастрюле на электроплите. Как в процессе кипения меняется температура и внутренняя энергия системы «вода–пар»? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
При кипении, температура системы "вода-пар" остается постоянной, а внутренняя энергия данной системы увеличивается, т.к. происходит поглощение тепловой энергии.
Задача 16
В вертикальном цилиндрическом сосуде под поршнем, способным перемещаться без трения, находится воздух.Как изменятся температура газа и его объём, если поршень быстро сместить вниз? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Объём | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если поршень быстро сместить вниз, то объем газа уменьшится, давление - увеличится, а так как давление связано с температурой соотношением: $p=nkT$, то и температура тоже увеличится.
Задача 17
В вертикальном цилиндрическом сосуде под поршнем, способным перемещаться без трения, находится воздух. Как изменятся давление газа и его внутренняя энергия, если поршень быстро сместить вверх? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Давление Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если поршень сместить вверх, то обмен с окружающейс средой произойти не успеет - процесс будет адиабатным. Тогда из 1 закона термодинамики $Q=0=A+∆U$, тогда $∆U=-A$. Газ расширяется, значит $A>0$, следовательно, и $∆U T_1$, то при повышении температуры воздуха скорость его молекул увеличится, это приведет к увеличению ударов молекул о стенки сосуда и поршня, а следовательно, к увеличению давления, что приведет к тому, что поршень сместится, увеличив объем газа, плотность же газа, уменьшится, поскольку $p=
В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ
В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ. Расстояния от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего одинаковы и равны h (рис.). Давление воздуха под верхним поршнем вдвое больше атмосферного. Вся система находится в равновесии. На верхний поршень надавливают так, что он опускается на место нижнего, сжимая газ. Каким станет расстояние х от нижнего поршня до дна сосуда? Атмосферное давление постоянно.

Обозначим h расстояние от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего, х — расстояние х от нижнего поршня до дна сосуда после сжатия, ратм — атмосферное давление, р1 — давление газа под верхним поршнем, рп — давление поршня, V1 — объем воздуха под верхним поршнем вначале, S — площадь основания поршней и дна цилиндра, р2 — давление под верхним поршнем после опускания верхнего поршня на место нижнего, рс — давление силы, придавившей поршень, V2 — новый объем воздуха под верхним поршнем, р3 — давление газа под нижним поршнем до опускания верхнего, р4 — давление газа под нижним поршнем после его сжатия, Т3 — объем воздуха под нижнем поршнем после сжатия.

Закон Бойля — Мариотта применительно к газу подверхним поршнем будет выглядеть так:
Давление газа под верхним поршнем р1 при равновесии равно сумме атмосферного давления ратм и давления поршня рп:
Но по условию задачи р1 = 2ратм, поэтому 2ратм = ратм + рп, откуда
Объем воздуха под верхним поршнем вначале был равен:
После опускания верхнего поршня на место нижнего газ под ними сжался и давление под верхним поршнем стало р2. Теперь оно равно сумме давлений атмосферы ратм, поршня рп и некоторой силы, придавившей поршень, рс:

Теперь нам предстоит решить систему уравнений (6) и (11) относительно искомого расстояния х, исключив из них неизвестные давления. Давайте в этих уравнениях сначала раскроем скобки и сделаем приведение подобных членов — может, мы их при этом немного упростим. Начнем с уравнения (6)
Идеальный одноатомный газ в количестве ν = 0, 09 моль находится в равновесии в вертикальном цилиндре под поршнем массой 5 кг?
Идеальный одноатомный газ в количестве ν = 0, 09 моль находится в равновесии в вертикальном цилиндре под поршнем массой 5 кг.
Трение между поршнем и стенками цилиндра отсутствует.
Внешнее атмосферное давление равно p = 100 кПа.
В результате нагревания газа поршень поднялся на высоту Δh = 4 см, а температура газа поднялась на ΔT = 16 К.
Чему равна площадь поршня?
Закон Менделеева - Клапейрона в руки.

A = p∆V = mR∆T / M = νR∆T.
А1 = mgh поднятие
A2 = paSh «расширение»
S = (νR∆T - mgh) / pah = 0.
0025 (м ^ 2) = 25 см кв.
В вертикальном цилиндре под подвижным поршнем площадью 40 см ^ 2 находится 1 моль идеального газа при температуре 400К?
В вертикальном цилиндре под подвижным поршнем площадью 40 см ^ 2 находится 1 моль идеального газа при температуре 400К.
Определить в литрах объем газа, если масса поршня равна 40кг, а атмосферное давление 100кПа.
Трением поршня о стенки цилиндра пренебречь.
Одноатомный газ количеством 2 моль находится в цилиндре с подвижным поршнем под атмосферным давлением?
Одноатомный газ количеством 2 моль находится в цилиндре с подвижным поршнем под атмосферным давлением.
В процессе нагревания температура увеличилась от 20 °C до 70°C, объем увеличился на 40л.
Которое количество теплоты было дано газу?
В откачанном пространстве вертикально стоит цилиндрический сосуд, перекрытый сверху подвижным поршнем массыМ?
В откачанном пространстве вертикально стоит цилиндрический сосуд, перекрытый сверху подвижным поршнем массыМ.
Под поршнем находится одноатомный газ при температуре Ти давлении Р.
Внутреннее сечение цилиндра S, высота той части сосуда, в которой находится газ, Н.
Поршень отпустили, он начал двигаться.
Чему равна максимальная скорость, развиваемая поршнем, если газ сжимается адиабатически?
В вертикальном цилиндре под невесомым поршнем находится идеальный газ?
В вертикальном цилиндре под невесомым поршнем находится идеальный газ.
Поршень может скользить по стенкам сосуда без трения.
Как изменится средняя кинетическая энергия поступательного движения молекул этого газа, если уменьшить объем газа под поршнем в 2 раза.
В цилиндре под поршнем находится идеальный газ?
В цилиндре под поршнем находится идеальный газ.
Надавливая на поршень, расстояние между поршнем и дном цилиндра уменьшают на треть.
Во сколько раз изменилось давление газа, если его температура поддерживалась постоянноя?
Среднее давление газов на поршень в цилиндре двигателя трактора 5000000 Па, ход поршня 15, 2 см, площадь 120 квад?
Среднее давление газов на поршень в цилиндре двигателя трактора 5000000 Па, ход поршня 15, 2 см, площадь 120 квад.
См. Чему равна работа за один ход поршня?
Под давлением газа поршень в цилиндре равномерно переместился на 4 см?
Под давлением газа поршень в цилиндре равномерно переместился на 4 см.
Какую работу выполнил газ?
Давление газа в цилиндре постоянно и равно 0, 6 МПа ; площадь поршня равна 0, 005м квадратных.
Под поршнем, который может свободно перемищаться в вертикальном цилиндре, ноходиться 2 моля одноатомного идеального газа?
Под поршнем, который может свободно перемищаться в вертикальном цилиндре, ноходиться 2 моля одноатомного идеального газа.
Какое количество теплоты надо сообщить газу, чтобы его темпиратура поднялась на 40К».
Одинаковая ли энергия потребуется для нагревания газа до одной и той же температуры : когда он находится в цилиндре с легкоподвижным поршнем ; когда поршень закреплен?
Одинаковая ли энергия потребуется для нагревания газа до одной и той же температуры : когда он находится в цилиндре с легкоподвижным поршнем ; когда поршень закреплен.
В цилиндре закрытом легкоподвижным поршнем массой m и площадью s находится газ?
В цилиндре закрытом легкоподвижным поршнем массой m и площадью s находится газ.
Объём газа равен Vо.
Каким станет Объём газа, если цилиндр передвигать вертикально с ускорением a вверх.
Атмосферное давление равно Pо, температура газа постоянна.
На этой странице сайта вы найдете ответы на вопрос Идеальный одноатомный газ в количестве ν = 0, 09 моль находится в равновесии в вертикальном цилиндре под поршнем массой 5 кг?, относящийся к категории Физика. Сложность вопроса соответствует базовым знаниям учеников 10 - 11 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.
В вертикальном цилиндре под невесомым поршнем находится идеальный газ. Поршень может двигаться без трения. Груз какой массы нужно положить на поршень, чтобы он оставался в прежнем положении, если температуру газа увеличить в 3 раза? Площадь поршня 10см^2 . Атмосферное давление 10^5 Па .

движению тела обычно препятствуют силы трения. если соприкасаются поверхности твердых тел, их относительному движению мешают силы сухого трения. характерной особенностью сухого трения является существование зоны застоя. тело нельзя сдвинуть с места, пока абсолютная величина внешней силы не превысит определенного значения. до этого момента между поверхностями соприкасающихся тел действует сила трения покоя, которая уравновешивает внешнюю силу и растет вместе с ней (рис. 1).
максимальное значение силы трения покоя определяется формулой
где μ— коэффициент трения, зависящий от свойств соприкасающихся поверхностен; n — сила нормального давления.
когда абсолютная величина внешней силы превышает значение fтр max, возникает относительное движение — проскальзывание. сила трения скольжения обычно слабо зависит от скорости относительного движения, и при малых скоростях ее можно считать равной fтр max.
движению тела в жидкости и газе препятствуют силы жидкого трения. главное отличие жидкого трения от сухого — отсутствие зоны застоя. в жидкости или газе не возникают силы трения покоя, и поэтому даже малая внешняя сила способна вызвать движение тела. сила жидкого трения при малых скоростях пропорциональна скорости, а при больших — квадрату скорости движения.
1. при экстренной остановке поезда, двигающегося со скоростью υ = 70 км/ч. тормозной путь составил s = 100 м. чему равен коэффициент трения между колесами поезда и рельсами? каким станет тормозной путь, если откажут тормоза в одном из n = 10 вагонов? массу локомотива принять равной массе вагона; силами сопротивления воздуха пренебречь.
при торможении ускорение а поезду сообщает сила трения fтр:
где μ — масса всего состава. сила трения представляет собой равнодействующую всех сил трения, действующих на состав (рис. 2), и равна по модулю .
с другой стороны, . подставляя это значение в выражение для μ, получаем
в том случае, когда не работают тормоза у одного из вагонов, суммарная сила трения, действующая на вагоны и локомотив, равна
где m — масса одного вагона. масса всего состава равна μ = (п + 1)∙m, так что . ускорение поезда в этом случае равно
Решение задач «Текст вопроса В цилиндре под поршнем находится один моль одноатомного. »,
физика
Текст вопроса В цилиндре под поршнем находится один моль одноатомного.
ID (номер) заказа
Текст вопроса В цилиндре под поршнем находится один моль одноатомного идеального газа. Газ расширяется от объема V0=0,4м3 до объема V1=2,3м3 , при этом его температура меняется по закону T=T0(p/p0)2, где параметры T0=556K; P0=48кПа. Найти работу, совершенную газом в этом процессе. Результат представить в мегаджоулях. Значение универсальной газовой постоянной считать равным R=8.31Джмоль?K.
Закажите подобную или любую другую работу недорого




Вы работаете с экспертами напрямую,
не переплачивая посредникам, поэтому
наши цены в 2-3 раза ниже 


Последние размещенные задания
социальная поддержка семей, имеющих детей в Республике.
Курсовая, Организация работы органов и учреждений социальной защиты населения и органов Пенсионного фонда Росс
Срок сдачи к 25 авг.
Рассчитать ректификацию системы ацетон-вода.
Курсовая, технология химических производств, технологическая химия
Срок сдачи к 10 сент.
Решение задач по машинному обучению в информационных системах.
Решение задач, Информатика и программирование
Срок сдачи к 14 авг.
помощь по самостоятельной работе.
Срок сдачи к 14 авг.
тема: Договор: форма, содержание, виды
Курсовая, Гражданское право
Срок сдачи к 18 авг.
Психология труда, инженерная психология и эргономика
Срок сдачи к 16 авг.
помочь сделать процессуальный документ
Другое, арбитражный процесс
Срок сдачи к 14 авг.
Необходимо решить тест более 90 баллов
Тест дистанционно, Социология
Срок сдачи к 15 авг.
Сделать отчет по практике
Отчет по практике, Педагогика
Срок сдачи к 23 авг.
Перефразировать уже имеющуюся работу
Диплом, Социальный работник, муниципальное управление, социология
Срок сдачи к 27 авг.
Необходимо решить тест более 90 баллов.
Тест дистанционно, мировая экономика
Срок сдачи к 15 авг.
Индивидуальный проект на любую тему для 10-11.
Срок сдачи к 27 авг.
Контрольная, Оценка регулирующего воздействия, муниципальное управление
Срок сдачи к 17 авг.
2. идеи педагогических инноваций в сфере профессионального образования
Другое, педагогика профессионального образования
Срок сдачи к 31 авг.
Все готово, надо просто учесть замечания преподавателя
Отчет по практике, Примеры, информатика
Срок сдачи к 17 авг.
Срок сдачи к 14 авг.
Адаптация детей к детскому саду 3-4 года, ( страниц 4
Доклад, Адаптация детей к детскому саду 3-4 года, педагогика
Срок сдачи к 17 авг.
Доклад, физическая культура
Срок сдачи к 20 авг.
обратились к нам
за последний год
работают с нашим сервисом
заданий и консультаций
заданий и консультаций
выполнено и сдано
за прошедший год


Сайт бесплатно разошлёт задание экспертам.
А эксперты предложат цены. Это удобнее, чем
искать кого-то в Интернете 

Отклик экспертов с первых минут
С нами работают более 15 000 проверенных экспертов с высшим образованием. Вы можете выбрать исполнителя уже через 15 минут после публикации заказа. Срок исполнения — от 1 часа
Цены ниже в 2-3 раза
Вы работаете с экспертами напрямую, поэтому цены
ниже, чем в агентствах
Доработки и консультации
– бесплатны
Доработки и консультации в рамках задания бесплатны
и выполняются в максимально короткие сроки
Гарантия возврата денег
Если эксперт не справится — мы вернем 100% стоимости
На связи 7 дней в неделю
Вы всегда можете к нам обратиться — и в выходные,
и в праздники

Эксперт получил деньги за заказ, а работу не выполнил?
Только не у нас!
Деньги хранятся на вашем балансе во время работы
над заданием и гарантийного срока
Гарантия возврата денег
В случае, если что-то пойдет не так, мы гарантируем
возврат полной уплаченой суммы


С вами будут работать лучшие эксперты.
Они знают и понимают, как важно доводить
работу до конца 


С нами с 2017
года
Помог студентам: 10 468 Сдано работ: 10 468
Рейтинг: 76 348
Среднее 4,95 из 5


С нами с 2018
года
Помог студентам: 6 897 Сдано работ: 6 897
Рейтинг: 59 663
Среднее 4,87 из 5


С нами с 2019
года
Помог студентам: 2 191 Сдано работ: 2 191
Рейтинг: 23 080
Среднее 4,85 из 5


С нами с 2018
года
Помог студентам: 1 909 Сдано работ: 1 909
Рейтинг: 11 765
Среднее 4,86 из 5

1. Сколько стоит помощь?
Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.
Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат. Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.
3. Выполняете ли вы срочные заказы?
Да, у нас большой опыт выполнения срочных заказов.
4. Если потребуется доработка или дополнительная консультация, это бесплатно?
Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.
5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?
Да, конечно - оценка стоимости бесплатна и ни к чему вас не обязывает.
6. Каким способом можно произвести оплату?
Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.д.
7. Предоставляете ли вы гарантии на услуги?
На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.
Идеальный газ находится в цилиндре под поршнем поршень быстро передвигают
Здесь приведены справочные данные, которые могут понадобиться вам при выполнении работы.
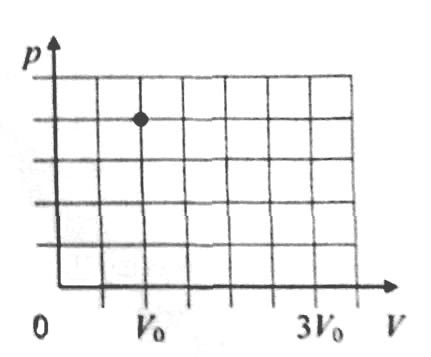
С1. В цилиндре под поршнем при комнатной температуре t0 долгое время находится только вода и ее пар. Масса жидкости в два раза меньше массы пара. Первоначальное состояние системы показано точкой на pV-диаграмме. Медленно перемещая поршень, объём V под поршнем изотермически увеличивают от V0 до 3V0. Постройте график зависимости давления ρ в цилиндре от объема V на отрезке от V0 до 3V0. Укажите, какими закономерностями Вы при этом воспользовались. (Решение)
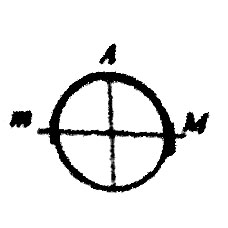
С2. Система из грузов m и M и связывающей их легкой нерастяжимой нити в начальный момент покоится в вертикальной плоскости, проходящей перпендикулярно оси закрепленной цилиндрической трубы. Грузы находятся на горизонтальной прямой, пересекающей ось трубы (см. рисунок). В ходе возникшего движения груз m отрывается от поверхности трубы в ее верхней точке А. Найдите массу m, если Μ = 100 г. Размеры грузов ничтожно малы по сравнению с радиусом трубы. Трением пренебречь. Сделайте схематический рисунок с указанием сил, действующих на грузы. (Решение)
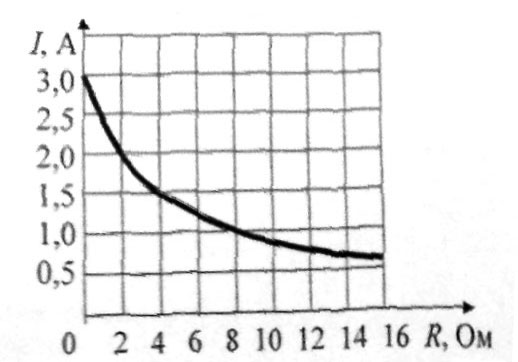
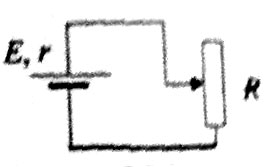
С4. Реостат R подключён к источнику тока с ЭДС Ε и внутренним сопротивлением r (см. рисунок) Зависимость силы тока в цепи от сопротивления реостата представлена на графике. Определите мощность тока, выделяемую на внутреннем сопротивлении источника при R = 4 Ом. (Решение)
С5. В таблице приведены значения силы тока в идеальном колебательном контуре, состоящем из конденсатора и катушки индуктивности, измеренные с точностью до 1 мА в последовательные моменты времени. Амплитуда напряжения на конденсаторе U = 5,0 В. Найдите значение индуктивности катушки. (Решение)
Идеальный газ находится в цилиндре под поршнем поршень быстро передвигают
С1-1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-3. В цилиндре, закрытом подвижным поршнем, находится газ, который может просачиваться сквозь зазор вокруг поршня. В опыте по изотермическому сжатию газа его объем уменьшился вдвое, а давление газа упало в 3 раза. Во сколько раз изменилась внутренняя энергия газа в цилиндре? (Газ считать идеальным.)
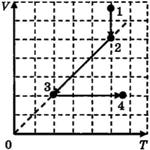
C1-5. Ha V T-диаграмме показано, как изменялись объём и температура некоторого постоянного количества разреженного газа при его переходе из начального состояния 1 в состояние 4. Как изменялось давление газа р на каждом из трёх участков 1—2, 2—3, 3—4: увеличивалось, уменьшалось или же оставалось неизменным? Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.
C1-6. В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают выдвигать из сосуда. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
С3-9. Нагреваемый при постоянном давлении идеальный одноатомный газ совершил работу 400 Дж. Какое количество теплоты было передано газу?
С3-11. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 8 раз, давление воздуха в сосуде увеличилось в 2 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)
С3-12. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 4 раза, давление воздуха в сосуде увеличилось тоже в 4 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)
С3-13. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔT. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на ΔT. Каким было изменение температуры ΔT в опытах? Масса азота m = 1 кг.
С3-14. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на 1 К. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на 1 К. Определите массу азота в опытах.
С3-15. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление p = 4 • 10 5 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газа поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3•10 3 H. Какое количество теплоты получил газ в этом процессе? Считать, что сосуд находится в вакууме.
С3-16. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 10 5 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты │Q│ = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня? Количество вещества газа постоянно.
С3-17. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа р1 = 4 · 10 5 Па. Расстояние от дна сосуда до поршня равно L. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтp = 3 · 10 3 Н. Найдите L. Считать, что сосуд находится в вакууме.
С3-18.Вертикальный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.
С3-19.В вертикальном теплоизолированном цилиндрическом сосуде под поршнем находится 0,5 моль гелия, нагретого до некоторой температуры. Поршень сначала удерживают, затем отпускают, и он начинает подниматься. Масса поршня 1 кг. Какую скорость приобретет поршень к моменту, когда поршень поднимется на 4 см, а гелий охладится на 20 К? Трением и теплообменом с поршнем пренебречь.
С3-20. Теплоизолированный сосуд объемом V = 2 м 3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль Не, а в другой — такое же количество моль А r . Температура гелия Т1 = 300 К, а температура аргона Т2 = 600 К. Определите парциальное давление аргона в сосуде после удаления перегородки.
Термодинамика С3-21. На рисунке изображено изменение состояния 1 моль идеального одноатомного газа. Начальная температура газа 27° С. Какое количество теплоты сообщено газу в этом процессе?
С3-23. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-24. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-25. На диаграмме (см. рисунок) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
Работа газа. Рассмотрим газ, находящийся в цилиндре с поршнем, позволяющем менять объем газа (рис 9.2)
Рассмотрим газ, находящийся в цилиндре с поршнем, позволяющем менять объем газа (рис 9.2). Отметим, что слово «газ» здесь совершенно условно. Это может быть жидкость, кристалл и вообще любое тело. Цилиндр контактирует с нагревателем или холодильником, который может сообщать газу тепло или отбирать его.
Пусть на поршень оказывается внешнее давление, величина которого может быть любой.
Все процессы, которые будем рассматривать ниже, будут квазистатическими, т.е. медленными настолько, чтобы можно было считать, что в каждый момент газ находится в состоянии т.д.р. Если очень быстро сжать газ, то давление его у поршня окажется на какой-то момент больше, чем в стальном объеме, и тогда нельзя будет говорить о давлении газа вообще. Такой процесс не является квазистатическим. Приближенно квазистатическими являются и процессы, достаточно быстрые с технической точки зрения, например процессы, происходящих в цилиндрах двигателя автомашины во время работы мотора (оказывается, для приближенной квазистатичности требуется, чтобы скорость поршня была мала по сравнению со скоростью звука в газе).
Работа над газом выполняется внешними силами при его сжатии. Работа самого газа выполняется при его расширении. Пусть газ расширяется так, что поршень на рис.9.2 поднимается на величину dx. Тогда газ выполнит работу (S – площадь поршня). Получим
Эта величина называется элементарной работой газа. Работа при расширении газа от объема V1до V2 будет равна
Если по одной оси отложить объем газа, по другой – его давление (плоскость P – V), то работа (9.9) будет изображаться площадью под кривой P(V) (рис.9.3).
Процесс расширения от объема V1 до объема V2 может происходить различным образом: например, можно при этом изолировать газ от нагревателя или, наоборот, нагревать газ и т.д. Иначе говоря, при перемещении из точки 1 в точку 2 в газе могут происходить различные процессы, даже если зафиксировано начальное и конечное состояния. В каждом процессе работа будет иметь свое значение, так как площадь под кривой процесса будет различной (кривые I, II, и III на рис.9.3). Таким образом, выполняемая газом работа зависит от процесса, который с ним происходит.
Заметим, что работа положительна, если она выполняется газом, и отрицательна, если внешние силы выполняют ее над газом.
Разделив величину силы на площадь поршня, получим давление P, а умножив на S, получим изменение объема газа dV . Таким образом, производимая над газом работа
dA= PdV. (2.30)
Такую же по величине работу совершает газ при расширении, перемещая поршень. При этом dV положительно, если газ расширяется, и отрицательно при сжатии газа. Соответственно работа dA положительна или отрицательна: в первом случае система производит работу сама, во втором — внешние силы производят работу над системой.
Графически процесс изменения состояния газа при его расширении или сжатии изображается на кривой P, V участком 1-2 на рис. Полная работа, совершаемая газом, при расширении от V1 до V2:
Эта работа численно равна заштрихованной площади, заключенной под кривой P(V).
Рассмотрим способы передачи телу тепла. При соприкосновении тел либо при взаимодействии тел через излучение, изменение внутренней энергии происходит за счет передачи энергии хаотически движущихся частиц одного тела частицам другого.
Энергия, передаваемая от одного тела другому, представляет собой теплоту. Обозначим ее через Q. Теплота измеряется в тех же единицах, что и энергия.
Связь между переданным теплом, изменением внутренней энергии системы и произведенной работой выражается уравнением
dQ = dE + dA = dE + PdV. (2.32)
Это уравнение представляет собой закон сохранения энергии применительно к механической и тепловой энергии макроскопических тел. Он получил название первого начала термодинамики.
Важно учесть, что в выражении (2.32) работа и количество тепла не есть полные дифференциалы каких-либо величин, в то время как внутренняя энергия является таковой. Можно говорить о внутренней энергии в данном состоянии, а не о количестве тепла или работы, которыми обладает тело. Нельзя делить энергию тела на тепловую и механическую, речь идет лишь об изменении внутренней энергии тела за счет количества тепла, переданного ему или отданного им, и количества совершенной работы. Это разделение неоднозначно и зависит от начального и конечного состояний тела и от характера совершаемого процесса. Поэтому, например, в процессе перехода из состояния 1 в состояние 2 изменение внутренней энергии может быть равно нулю, а тело при этом может приобрести или потерять энергию.
Читайте также: