Газ заполняет пространство между двумя длинными коаксиальными цилиндрами
Явления переноса в газах: Учебно-методическое обеспечение практического занятия , страница 3
Пример 4. Пространство между двумя коаксиальными цилиндрами заполнено азотом при давлении 101 кПа и температуре 20,0 °С. Радиусы цилиндров равны 10,0 и 10,5 см. Внешний цилиндр приводят во вращение с частотой 15,0 об/с. Какой момент нужно приложить к внутреннему цилиндру, чтобы он оставался неподвижным? Длина цилиндров 30,0 см.
В условии задачи неявно предполагается, что упорядоченное движение слоев газа между цилиндрами имеет ламинарный характер (без турбулентности), и так как , то краевыми эффектами можно пренебречь.
Слой молекул газа, адсорбированных внутренней поверхностью вращающегося цилиндра, будет обладать той же направленной скоростью, что и цилиндр, т. е.
Слой молекул газа, адсорбированных внешней поверхностью меньшего неподвижного цилиндра, будет неподвижным, т. е.
Сила, действующая на боковую поверхность внутреннего цилиндра, определяется по закону Ньютона для вязкости
где – градиент направленной скорости; – коэффициент внутреннего трения азота при заданных условиях; – площадь боковой поверхности внутреннего цилиндра.
Предполагаем, что направленная скорость газа в пространстве между цилиндрами (на расстоянии см) изменяется линейно с расстоянием. Тогда градиент направленной скорости можно рассчитать по следующей формуле:
Площадь боковой поверхности цилиндра
В данных условиях азот можно считать идеальным газом и коэффициент внутреннего трения азота может быть рассчитан по формуле
где – средняя длина свободного пробега; – средняя скорость молекул; – плотность.
Средняя длина свободного пробега молекул азота
где – эффективный диаметр молекул; – концентрация молекул; k – постоянная Больцмана; T – термодинамическая температура; p – давление. Эффективный диаметр молекул азота м.
Средняя скорость молекул
где – температура азота между цилиндрами; – молярная масса азота, .
Плотность газа найдем, используя уравнение состояния идеального газа,
Момент сил, действующий на внутренний цилиндр,
Подставим выражения (19.1) – (19.9) в формулу (19.10), сделаем преобразования и получим
Подставим числовые значения и получим
Пример 5. Между стенками дюаровского сосуда находится воздух. Площадь поверхности как внутренних, так и наружных стенок сосуда 600 . Расстояние между стенками 1 см. Температура наружных стенок 20 °С. Температура внутренних стенок 78 К (сосуд заполнен жидким азотом). Какое количество теплоты передается молекулами воздуха от наружных стенок к внутренним за 1 ч. Рассмотреть два случая: 1) давление воздуха до заполнения сосуда жидким азотом было 101 кПа; 2) давление воздуха до заполнения сосуда жидким азотом было 333 мкПа.
2.7. Явления переноса
Решебник Иродова И.Е. (1979) - Задача 2. 247
Один конец стержня, заключенного в теплоизолирующую оболочку, поддерживается при температуре T1, а другой конец — при температуре T2. Сам стержень состоит из двух частей, длины которых l1 и l2 и коэффициенты теплопроводности x1 и x2.
Решебник Иродова И.Е. (1979) - Задача 2. 246
Воспользовавшись формулой Пуазейля (1.7г), определить массу ц газа, протекающего в единицу времени через поперечное сечение трубы длины l и радиуса а, на концах которой поддерживаются постоянные давления р1 и р2.
Решебник Иродова И.Е. (1979) - Задача 2. 245
Решить предыдущую задачу, считая, что между дисками находится ультраразреженный газ с молярной массой М, температурой Т и под давлением р.
Решебник Иродова И.Е. (1979) - Задача 2. 244
Два одинаковых параллельных диска, оси которых совпадают, расположены на расстоянии h друг от друга. Радиус каждого диска а, причем а >> h. Один диск вращают с небольшой угловой скоростью со, другой диск неподвижен.
Решебник Иродова И.Е. (1979) - Задача 2. 243
Газ заполняет пространство между двумя длинными коаксиальными цилиндрами, радиусы которых R1 и R2, причем R1
Решебник Иродова И.Е. (1979) - Задача 2. 242
Гелий при нормальных условиях заполняет пространство между двумя длинными коаксиальными цилиндрами. Средний радиус цилиндров R, зазор между ними dR, причем dR
Решебник Иродова И.Е. (1979) - Задача 2. 241
Коэффициент теплопроводности гелия в 8,7 раза больше, чем у аргона (при нормальных условиях). Найти отношение эффективных диаметров атомов аргона и гелия.
Решебник Иродова И.Е. (1979) - Задача 2. 240
Зная коэффициент вязкости гелия при нормальных условиях, вычислить эффективный диаметр его атома.
Решебник Иродова И.Е. (1979) - Задача 2. 239
Найти показатель политропы n процесса, совершаемого идеальным газом, при котором остается неизменным коэффициент: а) диффузии; б) вязкости; в) теплопроводности.
Решебник Иродова И.Е. (1979) - Задача 2. 238
Идеальный газ состоит из жестких двухатомных молекул. Как и во сколько раз изменятся коэффициенты диффузии D и вязкости h, если объем газа адиабатически уменьшить в n=10 раз?
Газ заполняет пространство между двумя длинными коаксиальными цилиндрами
Динамика движения заряженных частиц зависит от конкретных условий протекания тока. Важным частным примером является ток в металлах. Опыт показывает, что в данном случае плотность тока пропорциональна электрическому полю. Это означает, что на движущийся в металле электрон действует как бы сила трения, пропорциональная скорости электрона. Коэффициент пропорциональности между плотностью тока и полем называется проводимостью.
Трение вызвано взаимодействием электронов с ионами решетки. Если считать, что после столкновения средняя скорость электрона (сферически-симметричное рассеяние), то сила трения
где — частота столкновений, которая зависит от длины свободного пробега (от одного столкновения до другого) и от скорости электрона: Величины а значит, и можно приближенно считать постоянными. Отсюда и вытекает закон (21.1) с постоянной о. Здесь существенно, что см/с (см. § 20).
Установившаяся скорость движения электронов определяется из условия
Отсюда плотность тока и проводимость
Заметим, что о имеет в гауссовой системе размерность частоты. С помощью оценки (21.4) можно определить длину свободного пробега по экспериментальному значению . Для меди находим см.
Это примерно в 100 раз больше межатомного расстояния в решетке. Такой большой пробег не объясним с точки зрения классической механики, которая предсказывает величину порядка межатомных расстояний. По квантовой механике в идеальной решетке вообще нет трения. Рассеяние возникает только за счет нерегулярных искажений структуры решетки, главным образом вследствие тепловых колебаний атомов. Ясно, что и должны заметным образом зависеть от температуры.
Рассмотрим протекание постоянного тока по тонкому длинному проводнику. В этом случае можно считать, что плотность тока постоянна по сечению проводника. Следовательно, полный ток Пусть, далее, сечение проводника постоянно по его длине,
тогда так как полный ток не изменяется вдоль проводника. С другой стороны, полное напряжение (разность потенциалов) на концах проводника равно где — длина проводника. Подставляя полученные выражения в (21.1), найдем
называется сопротивлением проводника.
Закон пропорциональности тока и напряжения для металлических проводников был открыт экспериментально в 1826 г. немецким математиком и физиком Омом и носит его имя. Он ввел также понятие сопротивления и нашел его зависимость от параметров проводника (21.6). Интересно отметить, что Ом открыл свой закон, используя в качестве источника тока медно-висмутовую термопару с разностью температур 100 °С. Известные в то время гальванические элементы оказались, как обнаружил Ом, совершенно непригодными для таких опытов из-за неустойчивости их ЭДС и внутреннего сопротивления. Соотношение (21.1) носит название дифференциального закона Ома.
Единицей сопротивления в СИ является . В соответствии с этим единица проводимости в СИ есть 1 (Ом
Если сечение проводника изменяется достаточно медленно, так что в каждом сечении плотность тока однородна по сечению, то полное напряжение на проводнике
т. е. сопротивление такого проводника
Приведенное выражение справедливо и в общем случае произвольной проводящей среды, если под понимать сечение достаточно тонкой трубки тока. Под последней подразумевается область проводника, ограниченная линиями тока (см. § 6).
При протекании тока по сопротивлению электрические заряды проходят разность потенциалов При этом источник тока совершает работу переходящую в тепло из-за трения, механизм которого рассмотрен выше. Мощность, выделяющаяся на сопротивлении, равна (закон Джоуля — Ленца)
Задача. Пространство между бесконечно длинными коаксиальными идеально проводящими цилиндрами радиусов заполнено веществом с проводимостью а Найти распределение потенциала в пространстве между цилиндрами и сопротивление на единицу длины.
Уравнение непрерывности (20.4) совместно с законом Ома (21.1) дает
В цилиндрической системе координат (при условии аксиальной симметрии) имеем
Решение ищем в виде
Подставляя (21.11) в (21.10), находим и, удовлетворяя граничным условиям окончательно получим
Сопротивление на единицу длины найдем, вычислив полный ток:
Из уравнения (21.9) видно, что при задача о растекании тока по объемному проводнику сводится к уравнению Лапласа. Это обстоятельство иногда используется для моделирования электрических полей на так называемых электролитических ваннах.
Газ заполняет пространство между двумя длинными коаксиальными цилиндрами
В настоящий момент в базе находятся следующие задачи(номера задач соответствуют задачнику). Задачи, помеченные светло-зеленым цветом, можно купить. Базовая цена 30 руб. Подробней об оплате
Иродов_6.191. Вычислить, какая часть молекул газа: а) пролетает без столкновений расстояния, превышающие среднюю длину свободного пробега Я; б) имеет длины свободного пробега в интервале от X до 2Х.
Иродов_6.192. Узкий пучок молекул входит в сосуд с газом, давление которого достаточно низкое. Найти среднюю длину свободного пробега молекул пучка, если поток молекул в пучке убывает в т! раз на расстоянии Д/ вдоль пучка.
Иродов_6.193. Пусть adt — вероятность того, что молекула газа испытает столкновение в течение времени dt9 a - постоянная. Найти: 316а) вероятность того, что молекула не испытает столкновения в течение времени t; б) среднее время между столкновениями.
Иродов_6.194. Найти среднюю длину свободного пробега и среднее время между столкновениями молекул азота: а) при нормальных условиях; б) при Г=0°С и давлении р = 1, 0 нПа (такое давление позволяют получать современные вакуумные насосы).
Иродов_6.195. Во сколько раз средняя длина свободного пробега молекул азота, находящегося при нормальных условиях, больше среднего расстояния между его молекулами?
Иродов_6.196. Найти при нормальных условиях среднюю длину свободного пробега молекулы газа, для которого постоянная Ван-дер-Ваальса b-4Q см3/моль.
Иродов_6.197. Азот находится при нормальных условиях. При какой частоте колебаний длина звуковой волны в нем будет равна средней длине свободного пробега молекул данного газа?
Иродов_6.198. Кислород находится при О °С в сосуде с характерным размером /=10 мм (это линейный размер, определяющий характер интересующего нас процесса). Найти; а) давление газа, ниже которого средняя длина свободного пробега молекул Х>1; б) соответствующую концентрацию молекул и среднее расстояние между ними.
Иродов_6.199. Азот находится при нормальных условиях. Найти: а) число столкновений, испытываемых в среднем каждой молекулой за одну секунду; б) число всех столкновений между молекулами в 1 см3 азота ежесекундно.
Иродов_6.200. Как зависят средняя длина свободного пробега и число столкновений каждой молекулы в единицу времени от температуры Т идеального газа в следующих процессах: а) изохорическом; б) изобарическом?
Иродов_6.201. Идеальный газ совершил процесс, в результате которого его давление возросло в я раз. Как и во сколько раз изменились средняя длина свободного пробега и число столкновений каждой молекулы в единицу времени, если процесс: а) изохорический; б) изотермический?
Иродов_6.202. Идеальный газ, состоящий из жестких двухатомных молекул, совершает адиабатический процесс. Как зависят средняя длина свободного пробега и число столкновений каждой молекулы ежесекундно в этом процессе от: а) объема V; б) давления р; в) температуры
Иродов_6.203. Идеальный газ совершает политропический процесс с показателем политропы л. Найти среднюю длину свободного пробега и число столкновений каждой молекулы ежесекундно как функцию: а) объема V; б) давления р; в) температуры Г.
Иродов_6.204. Определить молярную теплоемкость идеального газа из жестких двухатомных молекул, совершающего политропический процесс, при котором число столкновений между молекулами в единицу времени остается неизменным: а) в единице объема; б) во всем объеме газа.
Иродов_6.205. Идеальный газ с молярной массой М находится в тонкостенном сосуде объемом К, стенки которого поддерживаются при постоянной температуре Т. В момент г=0 в стенке сосуда открыли малое отверстие площадью S, и газ начал вытекать в вакуум. Найти концентрацию п газа как функцию времени t, если в начальный момент п(0)=л0.
Иродов_6.206. Сосуд с газом разделен на две одинаковые половины 1 и 2 тонкой теплоизолирующей перегородкой с двумя отверстиями. Диаметр одного из них мал, а другого очень велик (оба - по сравнению со средней длиной свободного пробега молекул). В половине 2 газ поддерживается при температуре вх раз большей, чем в половине 7. Как и во сколько раз изменится концентрация молекул в половине 2, если закрыть только большое отверстие?
Иродов_6.207. В результате некоторого процесса вязкость идеального газа увеличилась в а =2, 0 раза, а коэффициент диффузии - в р=4, 0 раза. Как и во сколько раз изменилось давление газа?
Иродов_6.208. Как изменятся коэффициент диффузии D и вязкость т] идеального газа, если его объем увеличить в п раз: а) изотермически; б) изобарически?
Иродов_6.209. Идеальный газ состоит из жестких двухатомных молекул. Как и во сколько раз изменятся коэффициент диффузии D и вязкость т|, если объем газа адиабатически уменьшить в л = 10 раз?
Иродов_6.210. Найти показатель политропы п процесса, совершаемого идеальным газом, при котором неизменны: а) коэффициент диффузии; б) вязкость; в) теплопроводность.
Иродов_6.211. Зная вязкость гелия при нормальных условиях, вычислить эффективный диаметр его атома.
Иродов_6.212. Теплопроводность гелия в 8, 7 раза больше, чем у аргона (при нормальных условиях). Найти отношение эффективных диаметров атомов аргона и гелия.
Иродов_6.213. Гелий при нормальных условиях заполняет пространство между двумя длинными коаксиальными цилиндрами. Средний радиус цилиндров R, зазор между ними AR, причем АЛ Л. Внутренний цилиндр неподвижен, а внешний вращают с небольшой угловой скоростью . Момент сил трения, действующих на единицу длины внутреннего цилиндра, равен Nt. Найти вязкость газа, имея в виду, что сила трения, действующая на единицу площади цилиндрической поверхности радиуса г, определяется формулой о^цг(дь>1дг).
Иродов_6.215. Два одинаковых параллельных диска, оси которых совпадают, расположены на расстоянии h друг от друга. Радиус каждого диска равен а, причем a h, Один диск вращают с небольшой угловой скоростью о, другой диск неподвижен. Найти момент сил трения, действующий на неподвижный диск, если вязкость газа между дисками равна ц.
Иродов_6.216. Решить предыдущую задачу, считая, что между дисками находится ультраразреженный газ с молярной массой М, температурой Г и под давлением р.
Иродов_6.217. Воспользовавшись формулой Пуазейля (1. 7г), определить массу i газа, протекающего в единицу времени через поперечное сечение трубы длиной / и радиусом а, на концах которой поддерживаются постоянные давления рх и рг. Вязкость газа равна ц.
Иродов_6.218. Один конец стержня, заключенного в теплоизолирующую оболочку, поддерживается при температуре Tv а другой конец - при температуре Тг. Сам стержень состоит из двух частей, длины которых 1Х и 12 и теплопроводности xt и хг. Найти температуру поверхности соприкосновения этих частей стержня.
Иродов_6.219. Сложены торцами два стержня, длины которых 1Х и 1г и теплопроводности х х и х2. Найти теплопроводность однородного стержня длины 1х+129 проводящего теплоту так же, как и система из этих двух стержней. Боковые поверхности стержней теплоизолированы.
Иродов_6.220. Стержень длины I с теплоизолированной боковой поверхностью состоит из материала, теплопроводность которого319изменяется с температурой по закону х=а/Г, где а - постоянная. Торцы стержня поддерживают при температурах Г, и Г2. Найти зависимость Т(х)9 где х - расстояние от торца с температурой Гр а также плотность потока тепла.
Иродов_6.221. Два куска металла, теплоемкости которых Сх и С2, соединены между собой стержнем длины / с площадью поперечного сечения 5 и достаточно малой теплопроводностью х. Вся система теплоизолирована от окружающего пространства. В момент f=0 разность температур между двумя кусками металла равна (ДГ)0. Пренебрегая теплоемкостью стержня, найти разность температур между кусками металла как функцию времени.
Иродов_6.222. Пространство между двумя большими горизонтальными пластинами заполнено гелием. Расстояние между пластинами / = 50 мм. Нижняя пластина поддерживается при температуре Тг=290 К, верхняя - при 7^=330 К. Давление газа близко к нормальному. Найти плотность потока тепла.
Иродов_6.223. Гелий под давлением р = 1, 0 Па находится между двумя большими параллельными пластинами, отстоящими друг от друга на /=5, 0 мм. Одна пластина поддерживается при ^=17°С, другая — при *2=37°С. Найти среднюю длину свободного пробега атомов гелия и плотность потока тепла.
Иродов_6.224. Найти распределение температуры в пространстве между двумя коаксиальными цилиндрами с радиусами ^ и ^, заполненном однородным теплопроводящим веществом, если температуры цилиндров равны Т< и Т2.
Иродов_6.225. Тот же вопрос, что и в предыдущей задаче, но для двух концентрических сфер с радиусами Rx и /^ и температурами Тх и Г2.
Иродов_6.226. Постоянный электрический ток течет по проводу, радиус сечения которого R и теплопроводность х. В единице объема провода выделяется тепловая мощность w. Найти распределение температуры в проводе, если установившаяся температура на его поверхности равна Т0.
Иродов_6.227. В однородном шаре, радиус которого R и теплопроводность х, выделяется равномерно по объему тепловая мощность с объемной плотностью w. Найти распределение температуры в шаре, если установившаяся температура на его поверхности равна Г0.
Задачи для самостоятельного решения и контрольных заданий
1. Найти среднюю длину свободного пробега и среднее время между столкновениями молекул азота, находящегося: а) при нормальных условиях; б) при температуре t = 0° С и давлении p = 1 нПа (такое давление позволяет получать современные вакуумные насосы). [а) 0,06 мкм, 0,13 нс; б) 6 нм, 3,8 ч]
2. Баллон вместимостью V=10 л содержит водород массой m=1 г. Определить среднюю длину свободного пробега молекул.[1,55 нм]
3. Определить плотность разреженного водорода, если средняя длина свободного пробега [1,55 кг/м 3 ]
4. Найти зависимость среднего числа столкновений молекулы идеального газа в 1 с от давления при следующих процессах: 1) изохорном; 2) изотермическом. Изобразить эти зависимости на графиках.[1) ; 2) ]
5. Азот находится при нормальных условиях. Найти: а) число столкновений, испытываемых в среднем каждой молекулой за одну секунду; б) число всех столкновений, происходящих между молекулами в 1 см 3 азота ежесекундно. [а) 0,74×10 10 с -1 ; б) 1×10 29 с -1 см -3 ]
6. Оценить среднюю длину свободного пробега и коэффициент диффузии D ионов в водородной плазме. Температура плазмы 10 7 К, число ионов в 1 см 3 плазмы равно 10 15 . При указанной температуре эффективное сечение иона водорода считать равным 4×10 -20 см 2 . [ l
7. Найти, как зависят от давления средняя длина свободного пробега и число столкновений в 1 с молекул идеального газа, если газ совершает процесс: а) изохорический, б) изотермический, в) адиабатический. Эффективный диаметр молекул считать постоянным. а) , ; б) , .
8. Найти, как зависят от температуры средняя длина свободного пробега и число столкновений в 1 с молекул идеального газа, если масса газа постоянна и газ совершает процесс: а) изохорический, б) изобарический, в) адиабатический.
9. Зная коэффициент вязкости гелия при нормальных условиях (h = 18,9 мкПа×с), вычислить эффективный диаметр его атома. [d = 0,18 нм]
10. Коэффициент теплопроводности гелия в 8,7 раза больше, чем у аргона (при нормальных условиях). Найти отношение эффективных диаметров атомов аргона и гелия. [1,7]
11. Коэффициент диффузии кислорода (О2) при температуре 0°С равен 0,19 см 2 /с. Определить среднюю длину свободного пробега молекул газа. [1,35×10 -7 м]
12. Давление двухатомного газа вследствие сжатия увеличивается в 10 раз. Определить, как изменится длина свободного пробега молекул в газе и коэффициент вязкости газа. Рассмотреть случай, когда сжатие происходит: а) изотермически, б) адиабатически. [а) уменьшится в 10 раз; h останется неизменным, б) уменьшится в 5,2 раза, h увеличится в 1,39 раза]
13. Двухатомный газ адиабатически расширяется до объема, в два раза большего начального. Определить, как изменится коэффициент теплопроводности и коэффициент диффузии газа. [ уменьшится в 1,15 раза; D увеличится в 1,75 раза]
14. Между двумя параллельными плоскими очень большими пластинами имеется зазор а = 1 см. Между пластинами поддерживается разность температур DТ = 1 К (Т1 = 299,5 К, Т2 = 300,5 К). Зазор заполнен аргоном при давлении 1,0×10 5 Па. Оценить плотность потока тепла. [0,5 Вт/м 2 ]
15. Найти распределение температуры в пространстве между двумя коаксиальными цилиндрами с радиусами R1 и R2, заполненном однородным теплопроводящим веществом, если температуры цилиндров постоянны и равны соответственно Т1 и Т2. [ ]
16. Одноатомный идеальный газ заполняет пространство между двумя очень длинными коаксиальными цилиндрами с радиусами R1 и R2 (R2 > R1). Внутренний цилиндр поддерживается при температуре Т1, внешний при температуре Т2 (Т1 > Т2). Найти поток тепла, приходящийся на единицу длины цилиндров. Считать, что длина свободного пробега молекул газа много меньше расстояния между цилиндрами. [ ]
17. Через площадку S = 100 см 2 за время t = 10 с вследствие диффузии проходит некоторое количество азота. Градиент плотности в направлении, перпендикулярном площадке равен 1,26 кг/м 4 . Процесс идет при температуре 300 К, средняя длина свободного пробега молекул азота 10 -7 м, эффективный диаметр его молекул 3,75×10 -10 м. Определить количество продиффундировавшего азота за указанное время через площадку S.
18. Пространство между двумя большими параллельными пластинами заполнено средой, коэффициент теплопроводности которой изменяется с температурой по закону , где a0 – постоянная для данной среды величина. Температуры пластин Т1 и Т2 поддерживаются постоянными (Т1 > Т2). Расстояние между пластинами L. Найти плотность потока тепла и температуру Т в среде как функцию x, где x– расстояние отсчитанное от пластины, температура которой Т1.
Простейшие стационарные задачи теории теплопроводности
В стационарных задачах теории теплопроводности рассматриваются ситуации, когда распределение температуры в системе не меняется с течением времени.
1. Найдем распределение температуры в протяженной плоской пластине толщины l вдали от ее краев. Поверхности пластины поддерживаются при постоянных температурах Т1 и Т2 (рис. 24.1). Начало координат поместим на плоскости, ограничивающей пластинку слева. Ось х перпендикулярна пластине.
В стационарном случае температура в точках пластинки зависит только от координаты х и не зависит от времени. Тогда , и из уравнения (23.5) следует , т.е. плотность потока тепла постоянна. Вывод о постоянстве плотности потока тепла можно сделать и без ссылки на уравнение теплопроводности (23.5). Выделим мысленно внутри пластинки элемент объема в виде цилиндра или призмы, образующие которого параллельны оси х, а основания перпендикулярны. Так как температура внутри пластинки не меняется со временем, количество тепла, поступившего в этот объем в единицу времени, должно быть равно вышедшему количеству тепла. Значит, плотности потока тепла на основаниях выбранного объема должны быть одинаковы. Поэтому
Если пластинка однородна и k не зависит от температуры . Обозначая константу буквой А и интегрируя, получим
где В – еще одна постоянная интегрирования. Постоянные А и В можно найти из граничных условий. При х = 0 температура Т(0) = Т1, а при х = l T(l) = T2. Эти условия приводят к системе уравнений
T2 = Al + B.
Определив из нее постоянные А и В, найдем распределение температуры:
2. Найдем стационарное распределение температуры T(r) между двумя коаксиальными (имеющими общую ось) бесконечно длинными цилиндрами (рис. 24.2). Радиус внутреннего цилиндра обозначим R1, внешнего – R2. Пространство между цилиндрами заполнено однородным веществом. Температуры цилиндров поддерживаются постоянными и равными соответственно Т1 и Т2. Для определенности будем считать, что Т1 > Т2. Из симметрии рассматриваемой задачи следует, что во всех точках цилиндрической поверхности радиуса r (R1 < r < R2) температура одинакова. Градиент температуры dT/dr, а значит и вектор плотности потока тепла jнаправлены вдоль радиуса.
В установившемся режиме температура вещества в пространстве между цилиндрами не меняется со временем. Поэтому количества теплоты, проходящие в единицу времени через поверхности внутреннего и внешнего цилиндров, а также и через любую цилиндрическую поверхность между ними, должны быть одинаковы.
Учитывая, что площадь боковой поверхности цилиндра пропорциональна его радиусу r, последнее условие можно записать в виде:
Если можно пренебречь зависимостью коэффициента теплопроводности k от температуры, его можно внести в константу. Обозначая постоянную буквой А, получим
После интегрирования имеем
где В - константа интегрирования.
Как и в предыдущем случае, константы А и В определяем из граничных условий.
Решая эту систему, получим
После подстановки в (24.1) найдем распределение температуры T(r) в пространстве между цилиндрами
3. Рассмотрим задачу, в которой присутствуют источники тепла.
Найдем распределение температуры T(r) внутри шара радиуса R, в котором в результате какого-либо процесса (например, радиоактивного распада) происходит выделение тепла (рис.24.3). Количество тепла, выделяющееся в единицу времени в единице объема обозначим q. Будем считать, что q одинаково по всему объему и не меняется со временем. Теплопроводность вещества шара k. Температура Т0 на поверхности шара поддерживается постоянной.
В установившемся режиме температура внутри шара перестанет зависеть от времени. Тогда количество тепла, которое выделяется в единицу времени внутри сферической поверхности радиуса r должно быть равно количеству тепла, проходящему в единицу времени через эту поверхность
Проведя сокращения и разделив переменные, придем к уравнению
где В – постоянная интегрирования. Ее определим из граничного условия T(R) = T0.
Семинары 9, 10. Явления переноса
В состоянии термодинамического равновесия макроскопические параметры молекулярной системы не зависят от координат. Если система не изолирована, то макроскопические параметры (давление, температура, концентрация, электрический потенциал и др.) могут меняться от точки к точке. При наличии градиентов этих параметров в системе возникают потоки молекулярных свойств (внутренней энергии, импульса, концентрации), стремящиеся вернуть её в равновесное состояние.
Эти процессы носят название явлений переноса. К ним, в частности, относятся диффузия, теплопроводность, вязкость. В самых простейших случаях эти явления можно описать с помощью одномерных стационарных уравнений переноса.

, (9.1)
где In – плотность потока «меченых» частиц, D – коэффициент самодиффузии, n – концентрация «меченых» частиц.

, (9.2)
где IQ – плотность потока внутренней энергии, - коэффициент теплопроводности, Т – температура.

, (9.3)
где Imu – плотность потока импульса, - коэффициент вязкости, v – скорость слоя газа (жидкости).
Эти уравнения могут быть получены из обобщённого уравнения переноса для газов:

, (9.4)
где IG – поток молекулярного свойства G, n0 – концентрация, <v> - средняя скорость, - средняя длина свободного пробега молекул газа.
Течение газа через трубки описывается уравнениями, имеющими такую же математическую структуру, как и уравнения переноса.
Наиболее важными из них являются
а) течение Пуазейля (для плотного газа 
<< 2r), которое описывается уравнением

, (9.5)
где Q – масса ежесекундно протекающего через сечение трубы газа, r – радиус трубы, - плотность газа, - вязкость, P – давление газа;
б) кнудсеновское течение (для ультраразреженного газа, 
>>2r, через капилляры) описывается уравнением

, (9.6)
где N – поток молекул через сечение трубки S, n – концентрация разреженного газа.
З а д а ч и
9.1. На основе обобщённого уравнения переноса получить зависимость коэффициентов переноса (D,,) от микроскопических и макроскопических параметров системы.
9.2. Для измерения теплопроводности азота им наполнили пространство между двумя длинными коаксиальными цилиндрами, радиусы которых r1 = 0,5 см и r2 = 2 см. Внутренний цилиндр равномерно нагревается спиралью, по которой проходит ток силой i = 0,1 А. Сопротивление спирали, приходящееся на единицу длины цилиндра, равно R = 0,1 Ом. Внешний цилиндр поддерживается при температуре t2 = 0C. При установившемся процессе оказалось, что температура первого цилиндра t1 = 93C. Найти газокинетический диаметр молекулы азота. Давление газа таково, что конвекцией можно пренебречь.
9.3. Пользуясь полученной в задаче 9.1. зависимостью (T), найти стационарное распределение температуры в плоско-параллельном слое газа толщины l, на границах которого поддерживаются постоянные температуры T1 и T2. Нагревание производят таким образом, что конвекции не возникает. Найти также стационарное распределение температуры для сферичес-
кого и цилиндрического слоёв.
9.4. Через тонкую трубку ( >> 2r) течёт ультраразреженный газ. Оценить число молекул N, ежесекундно проходящих через поперечное сечение трубки длины l, если на одном её конце концентрация молекул n1, а на другом – n2. Течение считать изотермическим.
9.5. Определить, на какой угол повернётся диск, подвешенный на упругой нити, если под ним на расстоянии h = 1 см. вращается второй такой же диск с угловой скоростью = 50 рад/с. Радиус дисков R = 10 см, модуль кручения нити f = 100 динс/см. Краевыми эффектами пренебречь. Движение воздуха между дисками считать ламинарным.
9.6. Решить предыдущую задачу в предположении, что диски помещены в сильно разреженный воздух с P = 10 -4 мм.рт.ст., когда молекул воздуха велика по сравнению с расстоянием между дисками. Для упрощения расчёта считать, что все молекулы движутся с одинаковыми по абсолютному значению скоростями, равными средней скорости молекул воздуха V = 450 м/с.
9.7. Определить расход массы газа Q при стационарном изотермическом пуазейлевом течении его вдоль цилиндрической трубы длины l и радиуса r, на концах которой поддерживается давление P1 и P2 (P1 > P2).
9.8. Для определения вязкости углекислого газа им наполнили колбу с объёмом V = 1 л при давлении P1 = 1600 мм.рт.ст. Затем открыли кран, позволяющий CO2 вытекать из сосуда через капилляр длиною l = 10 см и диаметром D = 0,1 мм. Через время = 22 мин давление в колбе понизилось до P3 = 1350 мм.рт.ст. Вычислить из этих данных и газокинетический
диаметр молекулы CO2. Атмосферное давление P2 = 735 мм. рт. ст. Процесс считать изотермическим при температуре 15C.
О т в е т ы
9.1. 

,
.
9.2. 
.
9.3. 
для плоскопараллельного слоя 
=
для сферического слоя 
,
для цилиндрического слоя 
.
9.4. 
.
9.5.
.
9.6.
.
9.7.
.
9.8. 
,

.
Справочный материал
Постоянная Планка
.
Масса электрона
.
Заряд электрона
.
Число Авогадро
.
Постоянная Больцмана
.
Универсальная газовая постоянная
.
Объем моля идеального газа при нормальных условиях
.
Постоянная Лошмидта (число молекул в одном кубическом метре вещества, находящегося в состоянии идеального газа при нормальных условиях) 
.



(интеграл Пуассона)

Список литературы
Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высш. шк., 2000.
Иродов И.Е. Задачи по общей физике. – М.: Бином, 1998.
Матвеев А.Н. Молекулярная физика. – М.: Высш. шк., 1987.
Москвич О.И., Бомбенко О.Н. Общая физика. Молекулярная физика: Структурированный конспект лекций. Ч.1. – Красноярск, РИС КрасГУ, 2006.
Рейф Ф. Статистическая физика. Берклеевский курс физики. Т.5. – М.: Наука, 1986.
Сборник задач по общему курсу физики. Термодинамика и молекулярная физика. /Под ред. Д.В.Сивухина. – М.: Наука, 1976.
Каталог статей

Расстояние d между двумя точечными положительными зарядами Q1=9Q и Q2=Q равно 8 см. На каком расстоянии r от первого заряда находится точка, в которой напряженность E поля зарядов равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным? 
Условие задачи:
Два точечных заряда Q1=2Q и Q2=-Q находятся на расстоянии d друг от друга. Найти положение точки на прямой, проходящей через эти заряды, напряженность E поля в которой равна нулю. 
Условие задачи:
Электрическое поле создано двумя точечными зарядами Q1=40 нКл и Q2=-10 нКл, находящимися на расстоянии d=10 см друг от друга. Определить напряженность Е поля в точке, удаленной от первого заряда на r1=12 см и от второго на r2=6 см. 
14.7 
14.8 
14.9 
14.10
Условие задачи:
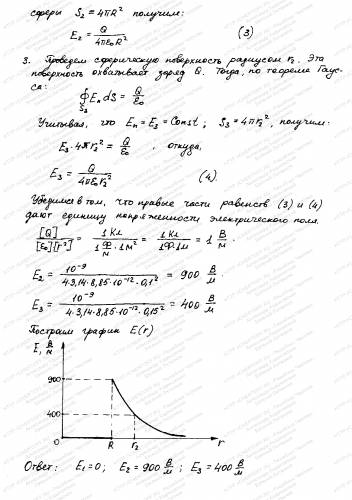
Две концентрические металлические заряженные сферы радиусами R1=6 см и R2=10 см несут соответственно заряды Q1=1 нКл и Q2=-0,5 нКл. Найти напряженности E поля в точках, отстоящих от центра сфер на расстояниях r1=5 см, r2=9 см, r3=15 см. Построить график зависимости E(r).
14.11

14.12

14.13
Условие задачи:
Прямой металлический стержень диаметром d=5 см и длиной l=4 м несет равномерно распределенный по его поверхности заряд Q=500 нКл. Определить напряженность E поля в точке, находящейся против середины стержня на расстоянии a=1 см от его поверхности.
14.14

14.15
Условие задачи:
Две длинные тонкостенные коаксиальные трубки радиусами R1=2 см и R2=4 см несут заряды, равномерно распределенные по длине с линейными плотностями τ1=1 нКл/м и τ2=-0,5 нКл/м. Пространство между трубками заполнено эбонитом. Определить напряженность Е поля в точках, находящихся на расстояниях r1= 1 см, r2=3 см, r3=5 см от оси трубок. Построить график зависимости Е от r.
14.16

14.17
Условие задачи:
Тонкий стержень длиной l=12 см заряжен с линейной плотностью τ=200 нКл/м. Найти напряженность Е электрического поля в точке, находящейся на расстоянии r=5 см от стержня против его середины.
14.18

14.19

14.20

14.22

14.23

14.24

14.25
Условие задачи:
Две бесконечные параллельные пластины равномерно заряжены с поверхностной плотностью σ1=10 нКл/м 2 и σ2=-30 нКл/м 2 . Определить силу взаимодействия между пластинами, приходящуюся на площадь S, равную 1 м 2 .
14.26

14.27
Условие задачи:
Построить графики зависимостей Е(r) и D(r).
Условие задачи:
Построить графики зависимостей E(r) и D(r).
Условие задачи:
Длинный парафиновый цилиндр радиусом R=2 см несет заряд, равномерно распределенный по объему с объемной плотностью ρ=10 нКл/м 3 . Определить напряженность E и смещение D электрического поля в точках, находящихся от оси цилиндра на расстоянии: 1) r1=1 см; 2) r2=3 см. Обе точки равноудалены от концов цилиндра. Построить графики зависимостей E(r) и D(r). 
14.30 
Решение задач «Пространство между двумя коаксиальными цилиндрами заполнено газом»,
Физика
Пространство между двумя коаксиальными цилиндрами заполнено газом. Радиус внешнего цилиндра – 20,5 см, внутреннего – 20 см. Длина обоих цилиндров равна 30 см. Внешний цилиндр вращается вокруг неподвижного внутреннего цилиндра с частотой 25 с-1 . Какая сила будет действовать на 1 м2 поверхности внутреннего цилиндра, если вязкость газа – 18 мкПа? С достаточной степенью точности слой газа между цилиндрами можно рассматривать как плоский.
Закажите подобную или любую другую работу недорого




Вы работаете с экспертами напрямую,
не переплачивая посредникам, поэтому
наши цены в 2-3 раза ниже 


Последние размещенные задания
нужна помощь в выполнении
Срок сдачи к 15 авг.
Срок сдачи к 18 авг.
Этапы подготовки и решения задач на ЭВМ
Срок сдачи к 19 авг.
социальная поддержка семей, имеющих детей в Республике.
Курсовая, Организация работы органов и учреждений социальной защиты населения и органов Пенсионного фонда Росс
Срок сдачи к 25 авг.
Рассчитать ректификацию системы ацетон-вода.
Курсовая, технология химических производств, технологическая химия
Срок сдачи к 10 сент.
Решение задач по машинному обучению в информационных системах.
Решение задач, Информатика и программирование
Срок сдачи к 14 авг.
помощь по самостоятельной работе.
Срок сдачи к 14 авг.
тема: Договор: форма, содержание, виды
Курсовая, Гражданское право
Срок сдачи к 18 авг.
Сделать отчет по практике
Отчет по практике, Педагогика
Срок сдачи к 23 авг.
помочь сделать процессуальный документ
Другое, арбитражный процесс
Срок сдачи к 14 авг.
Необходимо решить тест более 90 баллов
Тест дистанционно, Социология
Срок сдачи к 15 авг.
Психология труда, инженерная психология и эргономика
Срок сдачи к 16 авг.
Перефразировать уже имеющуюся работу
Диплом, Социальный работник, муниципальное управление, социология
Срок сдачи к 27 авг.
Необходимо решить тест более 90 баллов.
Тест дистанционно, мировая экономика
Срок сдачи к 15 авг.
Индивидуальный проект на любую тему для 10-11.
Срок сдачи к 27 авг.
Контрольная, Оценка регулирующего воздействия, муниципальное управление
Срок сдачи к 17 авг.
2. идеи педагогических инноваций в сфере профессионального образования
Другое, педагогика профессионального образования
Срок сдачи к 31 авг.
Все готово, надо просто учесть замечания преподавателя
Отчет по практике, Примеры, информатика
Срок сдачи к 17 авг.
обратились к нам
за последний год
работают с нашим сервисом
заданий и консультаций
заданий и консультаций
выполнено и сдано
за прошедший год


Сайт бесплатно разошлёт задание экспертам.
А эксперты предложат цены. Это удобнее, чем
искать кого-то в Интернете 

Отклик экспертов с первых минут
С нами работают более 15 000 проверенных экспертов с высшим образованием. Вы можете выбрать исполнителя уже через 15 минут после публикации заказа. Срок исполнения — от 1 часа
Цены ниже в 2-3 раза
Вы работаете с экспертами напрямую, поэтому цены
ниже, чем в агентствах
Доработки и консультации
– бесплатны
Доработки и консультации в рамках задания бесплатны
и выполняются в максимально короткие сроки
Гарантия возврата денег
Если эксперт не справится — мы вернем 100% стоимости
На связи 7 дней в неделю
Вы всегда можете к нам обратиться — и в выходные,
и в праздники

Эксперт получил деньги за заказ, а работу не выполнил?
Только не у нас!
Деньги хранятся на вашем балансе во время работы
над заданием и гарантийного срока
Гарантия возврата денег
В случае, если что-то пойдет не так, мы гарантируем
возврат полной уплаченой суммы


С вами будут работать лучшие эксперты.
Они знают и понимают, как важно доводить
работу до конца 


С нами с 2017
года
Помог студентам: 10 468 Сдано работ: 10 468
Рейтинг: 76 348
Среднее 4,95 из 5


С нами с 2018
года
Помог студентам: 6 897 Сдано работ: 6 897
Рейтинг: 59 663
Среднее 4,87 из 5


С нами с 2019
года
Помог студентам: 2 191 Сдано работ: 2 191
Рейтинг: 23 080
Среднее 4,85 из 5


С нами с 2018
года
Помог студентам: 1 909 Сдано работ: 1 909
Рейтинг: 11 765
Среднее 4,86 из 5

1. Сколько стоит помощь?
Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.
Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат. Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.
3. Выполняете ли вы срочные заказы?
Да, у нас большой опыт выполнения срочных заказов.
4. Если потребуется доработка или дополнительная консультация, это бесплатно?
Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.
5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?
Да, конечно - оценка стоимости бесплатна и ни к чему вас не обязывает.
6. Каким способом можно произвести оплату?
Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.д.
7. Предоставляете ли вы гарантии на услуги?
На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.
Читайте также:

