1 моль одноатомного газа в цилиндре под поршнем нагревается при постоянном давлении от 1
1 моль одноатомного газа в цилиндре под поршнем нагревается при постоянном давлении от 1
2011 год 109 вариант СЗ
В сосуде лежит кусок льда. Температура льда t1 = 0°С. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20°С? Тепловыми потерями на нагрев сосуда пренебречь. (Решение)
2011 год. 01-2 вариант. С3
В бутылке объемом V = 1 л находится гелий при нормальном атмосферном давлении. Горлышко бутылки площадью S = 2 см 2 заткнуто короткой пробкой, имеющей массу m = 20 г. Если бутылка лежит горизонтально, то для того, чтобы медленно вытащить из ее горлышка пробку, нужно приложить к пробке горизонтально направленную силу F = 1 Н. Бутылку поставили на стол вертикально горлышком вверх. Какое количество теплоты нужно сообщить гелию в бутылке для того, чтобы он выдавил пробку из горлышка? (Решение)
2011 год. 01-1 вариант. С3
Один моль идеального одноатомного газа переводят из состояния 1 с температурой Т1 = 300 К в состояние 2 таким образом, что в течение всего процесса давление газа возрастает прямо пропорционально его объему. В ходе этого процесса газ получает количество теплоты Q = 14958 Дж. Во сколько раз n уменьшается в результате этого процесса плотность газа? (Решение)
2010 год. 11 вариант. С1
В кабинете физики проводились опыты с разреженным газом постоянной массы. По невнимательности ученик, отметив на графике начальное и конечное состояния газа (см. рисунок), не указал, какие две величины из трёх (давление р, объём V, температура Т) отложены по осям. В журнале осталась запись, согласно которой названные величины изменялись следующим образом: p1 < р2, V1 > V2, Τ1 < Ί2. Пользуясь этими данными, определите, какие величины были отложены на горизонтальной и вертикальной осях. Ответ поясните, указав, какие физические закономерности вы использовали. (Решение)
2010 год 304 вариант СЗ
Некоторое количество одноатомного идеального газа расширяется из одного и того же начального состояния (p1, V1) до одного и того же конечного объёма V2 первый раз по изобаре, а второй - по адиабате (см. рисунок). Отношение количества теплоты Q12, полученного газом на изобаре от нагревателя, к модулю изменения внутренней энергии газа |U3 — U1| на адиабате k = Q12/|U3 — U1| = 6 . Чему равно отношение х работы газа на изобаре А12 к работе газа на адиабате А13? (Решение)
2010 год. 135 вариант. С5
В цилиндр закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие площадью 5·10 -4 м 2 , закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии невесомым стержнем длиной 0,5 м, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). Расстояние АВ равно 0,1 м. К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите объём цилиндра. (Решение)
2009 год. 133 вариант. С1
В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают вдвигать в сосуд. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните. (Решение)
2009 год. 133 вариант. С3
Один моль одноатомного идеального газа переходит из состояния 1 в состояние 3 в соответствии с графиком зависимости его объёма V от температуры T (T0 = 100 К). На участке 2 − 3 к газу подводят 2,5 кДж теплоты. Найдите отношение работы газа А123 ко всему количеству подведенной к газу теплоты Q123. (Решение)
2009 год. 304 вариант. С3
Постоянная масса одноатомного идеального газа совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты QH = 8 кДж. Какую работу совершают внешние силы при переходе газа из состояния 2 в состояние 3? (Решение)

2008 год. 131 вариант. С2
Разогретый сосуд прикрыли поршнем, который с помощью вертикальной нерастяжимой нити соединили с потолком. На сколько процентов от начальной понизится температура воздуха в сосуде к моменту, когда сосуд оторвется от поверхности, на которой он расположен? Масса сосуда 5 кг. Поршень может скользить по стенкам сосуда без трения. Площадь дна сосуда 125 см 2 . Атмосферное давление 10 5 Па. Тепловым расширением сосуда и поршня пренебречь. (Решение)
2008 год. 5941 вариант. С2
В калориметре находился m1 = 1 кг льда при температуре t1 = -5°С. После добавления в калориметр m2 = 25 г воды в нем установилось тепловое равновесие при температуре t = 0°С. Какова температура t2 добавленной в калориметр воды, если в калориметре оказался в итоге только лёд? Теплоёмкостью калориметра пренебречь. (Решение)
2008 год. 05205939 вариант. С2
В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз. На сколько градусов следует нагреть воздух в трубке, чтобы объём, занимаемый воздухом, стал прежним? Температура воздуха в лаборатории 300 К, а атмосферное давление составляет 750 мм рт.ст. (Решение)
2008 год. 2 вариант. С2
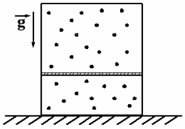
Вертикально расположенный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество водорода при температуре 361 К. Какая масса газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь. (Решение)
2007 год. 19 вариант. С2
В сосуде находится одноатомный идеальный газ, масса которого 12 г, а молярная масса 0,004 кг/моль. Вначале давление в сосуде было равно 4•10 5 Па при температуре 400 К. После охлаждения газа давление понизилось до 2•10 5 Па. Какое количество теплоты отдал газ? (Решение)
2006 год. 61 вариант. С2
В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м, закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объём воздуха в мешке достигает 28,0 м 3 - мешок всплывает вместе с прикреплённым к нему грузом. Масса оболочки мешка 2710 кг. Определите массу груза. Температура воды равна 7°С, атмосферное давление на уровне моря равно 10 5 Па. Объёмом груза и стенок мешка пренебречь. (Решение)
2006 год. 86 вариант. С2
Теплоизолированный сосуд объемом V = 2 м 3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль гелия, а в другой - такое же количество молей аргона. Начальная температура гелия равна 300 К, а температура аргона 600 К. Определите давление смеси после удаления перегородки. Теплоемкостью сосуда пренебречь. (Решение)
2006 год. 33 вариант. С2
Воздушный шар объемом 2500 м 3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м 3 . При какой минимальной разности температур воздуха внутри шара и снаружи шар взлетит вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Оболочку шара считать нерастяжимой. (Решение)
2006 год. 222 вариант. С2
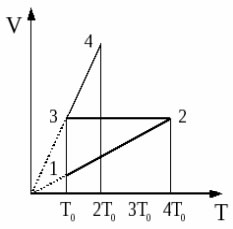
С одним молем идеального одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке в координатах V-Т. Во сколько раз количество теплоты, полученное газом в процессе 1-2-3-4, больше работы газа в этом процессе? (Решение)
2005 год. 58 вариант. С2
Идеальный одноатомный газ в количестве 1 моль сначала изотермически расширился при температуре T1 = 300 К. Затем газ изобарно нагрели, повысив температуру в 3 раза. Какое количество теплоты получил газ на участке 2-3? (Решение)
2004 год. 92 вариант. С2
10 моль одноатомного идеального газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты получил газ на участке 2-3? (Решение)
2004 год. 77 вариант. С5
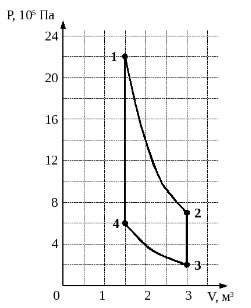
Идеальный одноатомный газ используется в качестве рабочего тела в тепловом двигателе. В ходе работы двигателя состояние газа изменяется в соответствии с циклом, состоящим из двух адиабат и двух изохор (см. рисунок). Вычислите КПД такого двигателя. (Решение)
2004 год. 49 вариант. С5
При электролизе воды образуется кислород О2 и водород Н2. Газы отводят в сосуд объёмом 100 л, поддерживая в нём температуру 300 К. Чему равна масса воды, которая разложилась в результате электролиза, чтобы суммарное давление в сосуде достигло 0,1 атм? Считать, что ничего не взрывается. (Решение)
2004 год. 35 вариант. С5
Смесь одинаковых масс гелия, водорода и азота помещена в сосуд и нагрета до температуры 350 К. Плотность смеси оказалась равной 50 г/м 3 . Чему равно давление в сосуде? (Решение)
1 моль одноатомного газа в цилиндре под поршнем нагревается при постоянном давлении от 1
В герметичном сосуде объёмом V0 = 1 литр под поршнем находится 1 моль идеального одноатомного газа при атмосферном давлении p0. На рисунке изображена pV-диаграмма, показывающая последовательные переходы этого газа из состояния 1 в состояние 5.
Выберите два верных утверждения на основании анализа представленного графика.
1) Работа газа в процессе 4–5 больше работы газа в процессе 2–3 в 1,5 раза.
2) В процессе перехода 4–5 газ совершил бόльшую работу, чем в процессе перехода 2–3–4.
3) Максимальное изменение ΔT температуры газа произошло в процессе 1–2.
4) Отношение разности температур газа в состояниях 5 и 3 к температуре газа в состоянии 1 равно 23.
5) Отношение температуры газа в состоянии 3 к температуре газа в состоянии 4 равно 1,25.
1) Работа газа численно равна площади под графиком pV-диаграммы.
3) Температура идеального газа равна Посчитаем изменения температур на участках:
Уже получили, что изменение температуры газа в процессе 1–2 не наибольшее.
В некотором процессе 1–2, который проводился с одним молем идеального одноатомного газа, среднеквадратичная скорость молекул газа возросла от u1 = 350 м/с до u2 = 380 м/с. При этом давление p газа в процессе оставалось постоянным, и газ совершил работу A = 292 Дж. Чему равна молярная масса этого газа?
1. Согласно молекулярно-кинетической теории идеального газа, среднеквадратичная скорость его молекул связана с температурой газа формулой
2. Работа газа при изобарическом (согласно условию) процессе равна
3. Из уравнения Клапейрона–Менделеева для одного моля идеального газа получаем, что
4. Таким образом, из записанных уравнений следует, что откуда
Один моль идеального одноатомного газа участвует в некотором процессе, в котором теплоёмкость газа постоянна. В начале этого процесса газ имеет давление 200 кПа и занимает объём 1 л. В ходе процесса газ расширяется до объёма 8 л и его давление становится равным 100 кПа. При этом газ получает от окружающих тел количество теплоты 1,8 кДж. Во сколько раз теплоёмкость газа в этом процессе превышает изохорическую молярную теплоёмкость одноатомного идеального газа?
Температуру в первом и во втором случае можно найти из закона Менделеева — Клапейрона: Тогда разность температур равна Молярная теплоёмкость вычисляется по формуле: Молярная теплоёмкость при постоянном объёме для одноатомного идеального газа равна: Найдём отношение теплоёмкостей:
Один моль идеального одноатомного газа совершает адиабатическое сжатие. Как изменяются в результате такого процесса давление и температура газа?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Согласно первому началу термодинамики, переданное газу тепло идет на увеличение его внутренней энергии и на совершение работы против внешних сил: Газ сжимается, значит, он совершает отрицательную работу Процесс сжатия адиабатический, следовательно, теплообмен с окружающей средой отсутствует Таким образом, внутренняя энергия увеличивается Внутренняя энергия идеального газа зависит только от температуры. При увеличении внутренней энергии температура увеличивается. Давление связано с объемом и температурой соотношением Таким образом, при адиабатическом уменьшении объема и увеличении температуры газа давление увеличивается.
На рисунке изображён график зависимости объёма V одного моля идеального одноатомного газа от его температуры T в процессе 1–2. Как в результате перехода из состояния 1 в состояние 2 изменяются внутренняя энергия газа и давление газа?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется.
Запишите в ответ цифры, расположив их в порядке, соответствующем таблице:
| Внутренняя энергия газа | Давление газа |
Внутренняя энергия идеального газа пропорциональна его температуре. Таким образом, при увеличении температуры, внутренняя энергия увеличивается.
Согласно уравнению перехода давление, объём и абсолютная температура идеального газа связаны соотношением
Из графика видно, что зависимость объема от температуры - квадратичная, т.е. имеет вид
Следовательно, отношение давлений имеет вид:
При переходе из состояния 1 в состояние 2 температура увеличивается, а значит, давление уменьшается.
Один моль идеального одноатомного газа совершает процесс 1–2–3, изображенный на рисунке. В процессе 1–2 температура газа постоянна и равна 300 К. Какое количество теплоты получил газ на участке 2–3?
В процессе 2–3 происходит изохорное нагревание газа. Работа газа равна нулю и, согласно первому началу термодинамики, переданное газу тепло в таком процессе идет только на изменение его внутренней энергии
При постоянном объеме для идеального газа выполняется закон Шарля, согласно которому Давление на участке 2–3 увеличилось в 3 раза, а значит, и температура увеличилась в 3 раза и стала равной 900 К.
Найдем количество теплоты, которое получил газ
Два моля идеального одноатомного газа находятся в состоянии 1 (см. рис.) при температуре 200 К. Газ совершает циклический процесс, изображённый на диаграмме. Какое количество теплоты получает газ на участке 1−2 этого циклического процесса? Ответ выразите в кДж и округлите до целого числа.
На участке 1−2 процесс изохорный, поэтому V1 = V2, следовательно, работа газа на участке 1−2 равна 0. По первому закону термодинамики Тогда на участке 1−2 количество теплоты равно изменению внутренней энергии газа. Изменение внутренней энергии одноатомного газа в этом случае равно Давление увеличилось от 0,5p0 до 5p0 при постоянном объёме. Следовательно, температура газа увеличилась так же в 10 раз. Значит, T2 = 10T1 = 2000 К. Отсюда
Один моль идеального одноатомного газа совершает циклический процесс 1-2-3-4-1, график которого показан на рисунке в координатах p-V. Из предложенного перечня выберите два верных утверждения и укажите их номера.
1) В процессе 1-2 внутренняя энергия газа увеличивается.
2) В процессе 2-3 газ совершает положительную работу.
3) В процессе 3-4 газу сообщают некоторое количество теплоты.
4) В процессе 4-1 температура газа увеличивается в 4 раза.
5) Работа, совершённая газом в процессе 1-2, в 3 раза больше работы, совершённой над газом в процессе 3-4.
Внутренняя энергия идеального газа пропорциональна температуре и не зависит от давления и занимаемого газом объема:
1) Процесс 1-2 -изобарное расширение. В этом процессе (согласно уравнению состояния идеального газа ) температура увеличивается, а значит и увеличивается внутренняя энергия. Утверждение верное.
2) В осях p-V работа газа равна площади под графиком. В процессе 2-3 работа газа равна нулю. Утверждение неверное.
3) Процесс 3-4 - изобарное сжатие, температура при этом уменьшается. Утверждение неверное.
4) Процесс 4-1 изохорное нагревание. Давление возрастает в 4 раза, а значит и температура возрастает в 4 раза. Утверждение верное.
5) Работа, совершённая газом в процессе 1-2, в 4 раза больше работы, совершённой над газом в процессе 3-4. Утверждение неверное.
На рисунке изображён график процесса 1–2–3–4 для двух молей идеального одноатомного газа. Какую работу совершила эта порция газа на изобарном участке данного процесса? Ответ выразите в Дж и округлите до целого числа.
Сначала нужно найти на графике изобарный участок. При (закон Гей-Люссака). Следовательно, то есть это прямая, проходящая через начало координат (отрезок 1–2). При этом При изобарном процессе работа газа
На рисунке изображён график циклического процесса, совершаемого одним молем идеального одноатомного газа. Определите, как в процессе перехода газа из состояния 3 в состояние 1 изменяются следующие физические величины: объём газа, внутренняя энергия газа.
Для каждой величины определите соответствующий характер изменения:
Запишите в ответ цифры, расположив их в порядке, соответствующем таблице:
| Объём газа | Внутренняя энергия газа |
Процесс 3−1 является изобарным охлаждением, а значит, объем газа в этом процессе уменьшается.
Внутренняя энергия газа является функцией температуры а значит, уменьшение температуры приведет к уменьшению внутренней энергии.
На рисунке изображён график процесса 1−2−3, совершаемого с пятью молями идеального одноатомного газа.
Выберите два верных утверждения относительно проведённого процесса.
1) Участок 1−2 представляет собой изотермическое сжатие.
2) На участке 2−3 температура газа увеличивается.
3) В состоянии 1 плотность газа минимальна.
4) В состоянии 3 концентрация молекул газа минимальна.
5) В состоянии 3 среднеквадратичная скорость молекул газа имеет максимальное значение.
1) Верно. Из графика находим, что P1V1 = 6p0V0; p2V2 = 6p0V0. Равенство p1V1 = p2V2 верно для изотермического процесса.
2) Неверно. На участке 2−3 происходит изобарное сжатие. Значит, температура уменьшается.
3) Верно. При неизменной массе плотность обратно пропорциональна объему. Из графика следует, что в точке 1 объем максимальный, следовательно, плотность минимальна.
4) Неверно. При неизменном числе молекул зависимость концентрации от объема обратно пропорциональна. В точке 3 объем минимальный, значит, концентрация максимальна.
5) Неверно. Из основного уравнения МКТ идеального газа
Ранее вычислили, что p1V1 = p2V2 = 6p0V0, в точке 3 p3V3 = 6p0V0. Следовательно, средняя квадратичная скорость молекул в точке 3 минимальна.
На рисунке изображён график процесса 1−2−3, совершаемого с пятью молями идеального одноатомного газа.
Выберите два верных утверждения относительно проведённого процесса.
1) На участке 1−2 температура газа увеличивается.
2) На участке 2−3 температура газа уменьшается.
3) В состоянии 1 плотность газа максимальна.
4) В состоянии 2 концентрация молекул газа максимальна.
5) В состоянии 3 среднеквадратичная скорость молекул имеет минимальное значение.
1) Неверно. Из графика находим, что P1V1 = 6p0V0; p2V2 = 6p0V0. Равенство p1V1 = p2V2 верно для изотермического процесса.
2) Верно. На участке 2-3 происходит изобарное сжатие. Значит, температура уменьшается.
3) Неверно. При неизменной массе плотность обратно пропорциональна объему. Из графика следует, что в точке 1 объем максимальный, следовательно, плотность минимальна.
4) Неверно. При неизменном числе молекул зависимость концентрации от объема обратно пропорциональна. В точке 2 объем не максимальный, значит, концентрация не максимальна.
5) Верно. Из основного уравнения МКТ идеального газа
Ранее вычислили, что p1V1 = p2V2 = 6p0V0, в точке 3 p3V3 = 6p0V0. Следовательно, средняя квадратичная скорость молекул в точке 3 минимальна.
Аналоги к заданию № 24100: 24153 Все
В тепловой машине один моль идеального одноатомного газа совершает процесс, изображенный на рисунке 1. Этот циклический процесс заменяют на другой, изображенный на рисунке 2, не изменяя ни газ, ни его количество. Как в результате изменятся следующие физические величины: передаваемое газу от нагревателя количество теплоты; совершаемая машиной механическая работа; КПД тепловой машины?
А) передаваемое газу от нагревателя количество теплоты за цикл
Б) совершаемая машиной механическая работа за цикл
Совершаемой за цикл тепловой машиной механической работе на диаграмме соответствует площадь цикла. Из диаграмм видно, что площадь обоих циклов одинаковая: Следовательно, совершаемая машиной механическая работа за цикл не изменяется (Б — 3).
Определить, что произойдёт с передаваемым газу от нагревателя количеством теплоты за цикл, немного сложнее. Подробно разберём оба цикла. На участках 1-2-3 объём газа увеличивается, его температура тоже увеличивается. Следовательно, по первому началу термодинамики, на этих участках тепло передаётся газу от нагревателя. На участках 3-4-1 температура и объём газа уменьшаются, а значит, тепло отводится от системы. Определим, сколько тепла передается газу на участках 1-2-3 (для этого потребуются первое начало термодинамики и уравнение Клапейрона — Менделеева). Для первого цикла:
Для второго цикла:
Таким образом, передаваемое газу от нагревателя тепло за цикл увеличивается (А — 1).
Наконец, КПД тепловой машины связано с работой за цикл и передаваемым газу теплом от нагревателя соотношением Поскольку в результате изменения цикла работа газа не изменяется, а передаваемое от нагревателя количество теплоты увеличивается, заключаем, что КПД тепловой машины уменьшается (В — 2).
Упражнение 15
Решение упражнений к учебнику Г.Я.Мякишева, Б.Б.Буховцева
1. Как изменится внутренняя энергия одноатомного идеального газа, если его давление увеличится в 3 раза, а объем уменьшится в 2 раза?

2. Термодинамической системе передано количество теплоты 200 Дж. Как изменилась внутренняя энергия системы, если при этом она совершила работу 400 Дж?

3. Стержень отбойного молотка приводится в движение сжатым воздухом. Масса воздуха в цилиндре за время хода поршня меняется от 0,1 до 0,5 г. Считая давление воздуха в цилиндре и температуру (27⁰C) постоянными, определите работу газа за один ход поршня. Молярная масса воздуха М = 0,029 кг/моль.

4. На одинаковые газовые горелки поставили два одинаковых плотно закупоренных сосуда вместимостью по 1 л. В одном сосуде находится вода, а в другом — воздух. Какой сосуд быстрее нагревается до 50 °С? Почему?

5. Предложен следующий проект вечного двигателя (рис. 13.12). Закрытый сосуд разделен на две половинки герметичной перегородкой, сквозь которую пропущены трубка и водяная турбина в кожухе с двумя отверстиями. Давление воздуха в нижней части больше, чем в верхней. Вода поднимается по трубке и наполняет открытую камеру. В нижней части очередная порция воды выливается из камеры турбины, подошедшей к отверстию кожуха. Почему данная машина не будет работать вечно?

6. Положительна или отрицательна работа газа в процессах 1—2, 2—3 и 3—1 на рисунке 10.5? Получает газ тепло или отдает в каждом из этих процессов?

7. Какое количество теплоты необходимо для изохорного нагревания гелия массой 4 кг на 100 К?

8. Вычислите увеличение внутренней энергии водорода массой 2 кг при изобарном его нагревании на 10 К. (Удельная теплоемкость водорода при постоянном давлении равна 14 кДж/(кг• К).)
9. В цилиндре компрессора сжимают идеальный одноатомный газ, количество вещества которого 4 моль. Определите, насколько поднялась температура газа за один ход поршня, если при этом была совершена работа 500 Дж. Процесс считайте адиабатным.

10. В калориметре находится вода массой 0,4 кг при температуре 10 °С. В воду положили лед массой 0,6 кг при температуре -40 ⁰С. Какая температура установится в калориметре, если его теплоемкость ничтожно мала?

11. Какой должна быть температура нагревателя, для того чтобы стало возможным достижение значения КПД тепловой машины 80%, если температура холодильника 27 °С?

12. В процессе работы тепловой машины за некоторое время рабочим телом было получено от нагревателя количество теплоты (Q1 = 1,5 •10 6 Дж, передано холодильнику Q2 = -1,2 • 10 6 Дж. Вычислите КПД машины и сравните его с максимально возможным КПД, если температуры нагревателя и холодильника соответственно равны 250 °С и 30 °С.
1 моль одноатомного газа в цилиндре под поршнем нагревается при постоянном давлении от 1
А23. Идеальный одноатомный газ находится в закрытом сосуде объёмом 0,6 м 3 . При охлаждении его внутренняя энергия уменьшилась на 1,8 кДж. В результате давление газа снизилось на
С1-1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-3. В цилиндре, закрытом подвижным поршнем, находится газ, который может просачиваться сквозь зазор вокруг поршня. В опыте по изотермическому сжатию газа его объем уменьшился вдвое, а давление газа упало в 3 раза. Во сколько раз изменилась внутренняя энергия газа в цилиндре? (Газ считать идеальным.)
С1-4. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
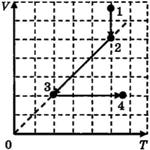
C1-5. Ha V T-диаграмме показано, как изменялись объём и температура некоторого постоянного количества разреженного газа при его переходе из начального состояния 1 в состояние 4. Как изменялось давление газа р на каждом из трёх участков 1—2, 2—3, 3—4: увеличивалось, уменьшалось или же оставалось неизменным? Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.
C1-6. В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают выдвигать из сосуда. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
C3-7.Идеальный одноатомный газ находится в сосуде объемом 1,2 м 3 под давлением 4•10 3 Па. Определите внутреннюю энергию этого газа. Ответ выразите в килоджоулях (кДж).
C3-8.Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,6 м 3 . При нагревании его внутренняя энергия увеличилась на 18 кДж. Насколько возросло давление газа? Ответ выразите в килопаскалях (кПа).
С3-9. Нагреваемый при постоянном давлении идеальный одноатомный газ совершил работу 400 Дж. Какое количество теплоты было передано газу?
С3-10. При изобарном нагревании газообразный гелий получил количество теплоты 100 Дж. Каково изменение внутренней энергии гелия? Масса гелия в данном процессе не менялась.
С3-11. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 8 раз, давление воздуха в сосуде увеличилось в 2 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)
С3-12. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 4 раза, давление воздуха в сосуде увеличилось тоже в 4 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)
С3-13. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔT. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на ΔT. Каким было изменение температуры ΔT в опытах? Масса азота m = 1 кг.
С3-14. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на 1 К. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на 1 К. Определите массу азота в опытах.
С3-15. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление p = 4 • 10 5 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газа поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3•10 3 H. Какое количество теплоты получил газ в этом процессе? Считать, что сосуд находится в вакууме.
С3-16. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 10 5 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты │Q│ = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня? Количество вещества газа постоянно.
С3-17. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа р1 = 4 · 10 5 Па. Расстояние от дна сосуда до поршня равно L. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтp = 3 · 10 3 Н. Найдите L. Считать, что сосуд находится в вакууме.
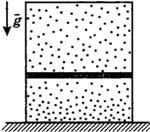
С3-18.Вертикальный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.
С3-19.В вертикальном теплоизолированном цилиндрическом сосуде под поршнем находится 0,5 моль гелия, нагретого до некоторой температуры. Поршень сначала удерживают, затем отпускают, и он начинает подниматься. Масса поршня 1 кг. Какую скорость приобретет поршень к моменту, когда поршень поднимется на 4 см, а гелий охладится на 20 К? Трением и теплообменом с поршнем пренебречь.
С3-20. Теплоизолированный сосуд объемом V = 2 м 3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль Не, а в другой — такое же количество моль А r . Температура гелия Т1 = 300 К, а температура аргона Т2 = 600 К. Определите парциальное давление аргона в сосуде после удаления перегородки.
С3-21. На рисунке изображено изменение состояния 1 моль идеального одноатомного газа. Начальная температура газа 27° С. Какое количество теплоты сообщено газу в этом процессе?

С3-22. На рисунке изображено изменение состояния 1 моль неона. Начальная температура газа 0°С. Какое количество теплоты сообщено газу в этом процессе?
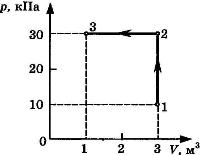
С3-23. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-24. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-25. На диаграмме (см. рисунок) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-26. Одноатомный идеальный газ неизменной массы совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты Qн = 8 кДж. Чему равна работа газа за цикл?
С3-27. С одноатомным идеальном газом неизменной массы происходит циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя?
С3-28. С разреженным азотом, который находится в сосуде с поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔТ. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на ΔТ. Каким было изменение температуры ΔТ в опытах? Масса азота m = 1 кг.
С3-29. Один моль аргона, находящийся в цилиндре при температуре T1 = 600 К и давлении p1 = 4•10 5 Па, расширяется и одновременно охлаждается так, что его давление при расширении обратно пропорционально квадрату объёма. Конечный объём газа вдвое больше начального. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A = 2493 Дж?
С3-30. Один моль аргона, находящийся в цилиндре при температуре T1 = 600 К и давлении p1 = 4•10 5 Па, расширяется и одновременно охлаждается так, что его давление при расширении обратно пропорционально квадрату объёма. Конечное давление газа p2 = 10 5 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A = 2493 Дж?
С3-31. Один моль одноатомного идеального газа переводят из состояния 1 в состояние 2 таким образом, что в ходе процесса давление газа возрастает прямо пропорционально его объёму. В результате плотность газа уменьшается в α = 2 раза. Газ в ходе процесса получает количество теплоты Q = 20 кДж. Какова температура газа в состоянии 1?
С3-32. Один моль аргона, находящийся в цилиндре при температуре T1 = 600 К и давлении p1 =4•10 5 Па, расширяется и одновременно охлаждается так, что его давление при расширении обратно пропорционально квадрату объёма. Конечное давление газа р2 = 10 5 Па. Какую работу совершил газ при расширении, если он отдал холодильнику количество теплоты Q = 1247 Дж?
С3-33. В сосуде объёмом V = 0,02 м 3 с жёсткими стенками находится одноатомный газ при атмосферном давлении. В крышке сосуда имеется отверстие площадью s, заткнутое пробкой. Максимальная сила трения покоя F пробки о края отверстия равна 100 Н. Пробка выскакивает, если газу передать количество теплоты не менее 15 кДж. Определите значение s, полагая газ идеальным.
С3-34. Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу А12 = 1000 Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу |A31| = 370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите количество теплоты |Qхол|, отданное газом за цикл холодильнику.
Термодинамика (страница 2)
По первому закону термодинамики \[Q=\Delta U+A,\quad (1)\] \(Q\) – количество теплоты, полученное системой, \(\Delta U\) – изменение внутренней энергии, \(A\) – работа газа.
А количество теплоты, полученное системой равно \[Q=Lm,\quad (2)\] где \(m\) – масса образовавшегося пара.
Так как процесс испарения прошел не до конца, то данный процесс изотермический, а значит работа газа будет совершаться за счет изменения массы пара \[A=\dfrac
Объединим (1), (2) и (3) и найдем отношение \(\dfrac<\Delta U>\) \[\dfrac<\Delta U>
=\dfrac
=1-\dfrac<\dfrac
Цикл тепловой машины, рабочим веществом которой является \(\nu\) молей идеального одноатомного газа, состоит из изотермического расширения, изохорного охлаждения и адиабатического сжатия. Работа, совершённая газом в изотермическом процессе, равна \(A\) , а КПД тепловой машины равен \(\eta\) . Максимальная температура в этом цикле равна \(T_o\) . Определите минимальную температуру \(T\) в этом циклическом процессе.
Процессы:
1-2 — изотермический
2-3 — изохорный
3-1 — адиабатический
КПД тепловой машины равен: \[\; \; \; \; \eta = \dfrac
Работа газа за цикл есть сумма работ газа в каждом процессе: \[A_\text <ц>= A_ <1-2>+ A_ <2-3>+ A_<3-1>\] Так как в процессе 2-3 объем газа постоянен, то его работа равна нулю.
Тогда работа газа за цикл равна: \[\; \; \; \; A_\text <ц>= A_ <1-2>+ A_ <3-1>\; \; \; \; (2)\] Далее необходимо найти количество теплоты \(Q_\text<н>\) , полученное газом от нагревателя.
Для этого запишем первое начало термодинамики для каждого процесса.
Процесс 1-2: \[Q_ <1-2>= A_ <1-2>+ \Delta U_<1-2>\] Так как процесс 1-2 изотермический, то изменение внутренней энергии газа \(\Delta U_<1-2>\) равно нулю.
Объем газа увеличивается, следовательно, газ совершает положительную работу.
Отсюда получаем, что: \[Q_ <1-2>= A_ <1-2>> 0 \; \; \; \Rightarrow \; \; \; \; Q_ <1-2>> 0\] Процесс 2-3: \[Q_ <2-3>= A_ <2-3>+ \Delta U_<2-3>\] Так как процесс 2-3 изохорный, то работа газа \(A_<2-3>\) равна нулю.
Давление газа уменьшается, следовательно, его температура также уменьшается (для изохорного процесса \(p \sim T\) ).
Следовательно, изменение внутренней энергии газа отрицательно.
Отсюда получаем, что: \[Q_ <2-3>= \Delta U_ <2-3>< 0 \; \; \; \Rightarrow \; \; \; \; Q_ <2-3>< 0\] Процесс 3-1:
Так как процесс 3-1 адиабатный, то \(Q_ <3-1>= 0\) : \[\; \; \; \; Q_ <3-1>= A_ <3-1>+ \Delta U_ <3-1>\; \; \; \Rightarrow \; \; \; \; A_ <3-1>= - \Delta U_ <3-1>\; \; \; \; (3)\] Таким образом, количество теплоты, полученное газом от нагревателя равно: \[Q_\text <н>= Q_<1-2>\] \[\; \; \; \; Q_\text <н>= A_ <1-2>\; \; \; \; (4)\] Подставим (2), (4) в (1): \[\eta = \dfrac
Подставим (7) в (6) и выразим искомую температуру: \[\eta = 1 - \dfrac<\dfrac<3><2>\nu R(T_1 - T_3)>
Следовательно, температура \(T_3\) является минимальной: \(T_3 = T\) .
Работа \(A_<1-2>\) совершена газом в изотермическом процессе: \(A_ <1-2>= A\) .
Таким образом, искомая температура равна: \[T = T_o - \dfrac<2> <3\nu R>(1 - \eta)A\]
Два одинаковых теплоизолированных сосуда соединены короткой трубкой с краном. В первом сосуде находится \(\nu_1\) =3 моль гелия при температуре \(T_1 = 350\) К, во втором \(\nu_2\) = 2 моль аргона при температуре \(T_2 = 400\) К. Кран открывают. В установившемся равновесном состоянии давление в сосудах становится \(p = 6 \) кПа. Определите объём \(V \) одного сосуда. Объёмом трубки пренебречь. Ответ дайте в м \(^3\) и округлите до тысячных.
Так как сосуды теплоизолированные, а газ не совершает работы, то изменение внутренней энергии равно 0, то есть \[U_1+U_2=U\] где \(U_1\) – внутренняя энергия первого сосуда, \(U_2\) – внутренняя энергия второго сосуда, \(U\) – внутренняя энергия сосудов после открытия краника.
Или \[\dfrac<3><2>\nu_1R T_1+\dfrac<3><2>\nu_2RT_2=\dfrac<3><2>\left(\nu_1+\nu_2\right)RT\] Отсюда установившаяся температура \[T=\dfrac<\nu_1T_1+\nu_2T_2><\nu_1+\nu_2>\] По закону Клапейрона – Менделеева \[p2V=\left(\nu_1+\nu_2\right)RT\] Отсюда объем одного сосуда \[V=\dfrac<\left( \nu_1T_1+\nu_2T_2\right)R><2p>=\dfrac <\left( 3\text< моль>\cdot 350\text< К>+2\text < моль>\cdot 400\text< К>\right)\cdot 8,31 \text< Дж/(моль$\cdot$ К)>><2\cdot 6\cdot 10^3 \text< Па>>\approx 1,28\text< м$^3$ >\]
1 моль идеального одноатомного газа сначала изотермически расширили. Затем изохорно нагрели, при этом его давление возросло в 3 раза (см. рисунок). Какое количество теплоты получил газ на участке 2–3, если \(T_1=100\) К? Ответ дайте в Дж.

1. Воспользуемся первым законом термодинамики \[Q=\Delta U+A,\] где \(Q\) – количество теплоты, полученное системой, \(\Delta U\) – изменение внутренней энергии системы, \(A\) – работа газа.
Так как процесс изохорный, то работа газа равна 0. Распишем изменение внутренней энергии и получим \[Q=\dfrac<3><2>\nu R \Delta T=\dfrac<3><2>\nu R \left(T_3-T_2\right)\] 2. Воспользуемся законом Шарля \[\dfrac
Один моль одноатомного идеального газа совершает процесс 1–2–3, график которого показан на рисунке в координатах T–V, Известно, что в процессе 1–2 газ совершил работу 3 кДж, а в процессе 2–3 объём газа V увеличился в 2 раза. Какое количество теплоты было сообщено газу в процессе 1–2–3, если его температура Т в состоянии 3 равна 600 К? Ответ дайте в Дж.

1.Проанализируем процессы
1–2 Процесс изотермический, по закон Бойля-Мариотта \[p_1 V_1=p_2V_2\] Значит возрастает объем и давление.
2–3 Температура увеличивается линейно объему, следовательно, процесс изобарный.
2. Количество теплоты, полученное в процессе 1–2–3, равно сумме количеств теплоты, полученных в процессах 1–2 и 2–3. \[Q_<123>=Q_<12>+Q_<23>\] 3. По первому закону термодинамики \[Q=\Delta U +A,\] где \(Q\) – количество теплоты, полученное системой, \(\Delta U\) – изменение внутренней энергии системы, \(A\) – работа газа.
Значит в процессе 1–2 изменение внутренней энергии равно 0, а количество теплоты \[Q_<12>=A_<12>=3 \text< кДж>\] В процессе 2–3 по условию объем возрос в 2 раза, значит по закону Гей-Люссака \[\dfrac
На рисунке показан циклический процесс постоянное количество одноатомного газа. Работу, которую совершают внешние силы при переходе газа из состояния 2 в состояние 3, равна 5 кДж. Какое количество теплоты газ отдаёт за цикл холодильнику? Ответ дайте в кДж 
Работа внешних сил в процессе 2–3 равна площади под графиком. \[A_<23>=\dfrac
Воспользуемся первым законом термодинамики \[|Q_<\text< хол>>|=|Q_<23>|=\Delta U_<23>+A_<32>=\dfrac<3><2>\left( \nu R T_2 -\nu R T_3\right)+ 3p_0V_0\quad (1)\] Также по уравнению Клапейрона – Менделеева \[p_2V_2=\nu R T_2= 2p_0 \cdot 3V_0 =6p_0V_0 \quad (2)\] \[p_2V_2=\nu R T_3=p_0V_0 \quad (3)\] Подставим в (1) формулы (2) и (3) \[|Q_<\text< хол>>|=\dfrac<3><2>\left(6p_0V_0-p_0V_0\right)+3p_0V_0= \dfrac<21><2>p_0V_0=\dfrac<7><2>A_<23>=3,5 \cdot 5\text < кДж>=17,5\text< кДж>\]
Читайте также:

