Равномерно заряженная нить на единицу длины которой приходится заряд лямбда имеет конфигурации
Теорема Остроградского—Гаусса и ее применение для расчета электростатических полей
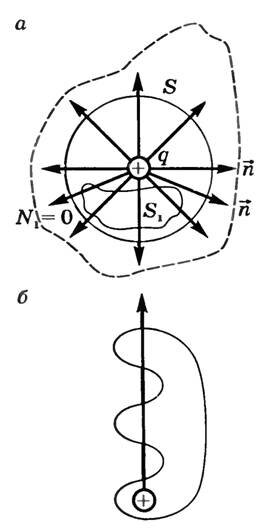
Пусть поле создается точечным электрическим зарядом q. Проведем замкнутую сферическую поверхность площадью S (рис. 2), окружающую этот заряд, центр которой совпадает с точкой нахождения заряда. Вычислим поток вектора напряженности через эту поверхность. За положительное направление нормали выберем направление внешней нормали \(~\vec n\). В этом случае во всех точках сферической поверхности E = const и cos α = 1.
Модуль напряженности поля на расстоянии R от заряда \(~E = \frac\). Площадь поверхности сферы \(~S = 4 \pi R^2\).
Следовательно, поток вектора напряженности через сферическую поверхность
Полученный результат будет справедлив и для поверхности произвольной формы, а также при любом расположении заряда внутри этой поверхности. Действительно, если окружить сферу произвольной замкнутой поверхностью (рис. 2, а — поверхность изображена штрихами), то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.
Если замкнутая поверхность произвольной формы охватывает заряд (рис. 2, б), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в поверхность, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линии, входящей в поверхность. Если же внутри поверхности площадью S1 (см. рис. 2) заряды отсутствуют, то поток напряженности через эту поверхность равен нулю (NS = 0).
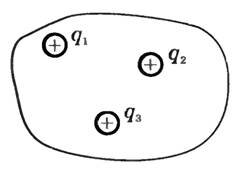
Если рассматриваемая поверхность охватывает не один, а несколько электрических зарядов, то под q следует понимать алгебраическую сумму этих зарядов (рис. 3) и
Эта формула выражает теорему Остроградского—Гаусса: поток вектора напряженности через замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на произведение электрической постоянной и диэлектрической проницаемости среды.
Применим эту теорему для расчета электростатических полей некоторых проводников.
Равномерно заряженная бесконечная плоскость
Пусть σ — поверхностная плотность заряда на плоскости (рис. 4).
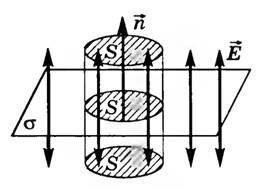
В качестве поверхности площадью S выберем цилиндрическую поверхность, образующая которой перпендикулярна плоскости. Основания этого цилиндра расположены перпендикулярно линиям напряженности по обе стороны от плоскости. Так как образующие цилиндра параллельны линиям напряженности (α = 90°, cos α = 0), то поток через боковую поверхность цилиндра отсутствует, и полный поток через поверхность цилиндра равен сумме потоков через два основания: N = 2ES. Внутри цилиндра заключен заряд q = σS, поэтому, согласно теореме Остроградского-Гаусса, \(~2ES = \frac\), где ε = 1 (для вакуума), откуда следует, что напряженность поля равномерно заряженной бесконечной плоскости
Бесконечная равномерно заряженная нить
Пусть τ — линейная плотность заряда нити. Выделим участок нити длиной Δl и окружим его цилиндрической поверхностью, расположенной так, что ось цилиндра совпадает с нитью (рис. 5).
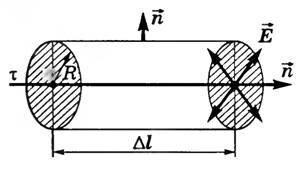
Линии напряженности электростатического поля, создаваемого нитью в сечении, перпендикулярном самой нити, направлены перпендикулярно боковой поверхности цилиндра, поэтому поток напряженности сквозь боковую поверхность \(~N = E \cdot 2 \pi R \Delta l\), где R — радиус цилиндра. Через оба основания цилиндра поток напряженности равен нулю (α = 90°, cos α = 0). Тогда полный поток напряженности через выделенный цилиндр
\(~N = E \cdot 2 \pi R \Delta l .\)
Заряд, находящийся внутри этого цилиндра, q = τ · Δl.
Согласно теореме Остроградского—Гаусса, можно записать \(~E \cdot 2 \pi R \Delta l = \frac\) . Следовательно, модуль напряженности поля, создаваемого равномерно заряженной бесконечно длинной нитью на расстоянии R от нее,
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 220-222.

Задание 14 № 23300
Положительный электрический заряд равномерно распределён по очень длинной непроводящей нити BC. Точка A находится напротив одного из концов этой нити, так, что отрезки AB и BC перпендикулярны. Куда направлен вектор напряжённости электростатического поля, создаваемого в точке A заряженной нитью? В качестве ответа запишите номер стрелки (целое число от 1 до 6).
Разделим длинную нить на малые участки, каждый из которых обладает одинаковым зарядом (по условию заряд распределен равномерно по всей нити). Каждый из этих участков создает в точке А электрическое поле напряжённостью вектор которого направлен из точки А по прямой, соединяющей этот малый участок (с учётом, что заряд положительный). При этом напряжённость поля, созданного точками, находящимися дальше вдоль нити, уменьшается, т. к. увеличивается расстояние до точки А. Общая напряжённость равна сумме векторов напряжённости Поэтому можно сделать вывод, что результирующий вектора напряжённости поля, созданного заряженной нитью в точке А, будет направлен по стрелке 5.

E = sigma\/(2*pi*R*eo) - \u043d\u0430\u043f\u0440\u044f\u0436\u0435\u043d\u043d\u043e\u0441\u0442\u044c \u0441\u043e\u0437\u0434\u0430\u0432\u0430\u0435\u043c\u0430\u044f \u0440\u0430\u0432\u043d\u043e\u043c\u0435\u0440\u043d\u043e \u0437\u0430\u0440\u044f\u0436\u0435\u043d\u043d\u043e\u0439 \u043d\u0438\u0442\u044c\u044e
E = Q\/(L*2*pi*R*eo)
F=E*q=Q*q\/(L*2*pi*R*eo) = 2*Q*e\/(L*2*pi*R*eo) = Q*e\/(L*pi*R*eo)
1) \u041d\u0430 \u043a\u0430\u043a\u043e\u043c \u0440\u0430\u0441\u0441\u0442\u043e\u044f\u043d\u0438\u0438 \u043e\u0442 \u043d\u0438\u0442\u0438 \u043d\u0430\u0445\u043e\u0434\u0438\u0442\u0441\u044f \u043f\u044b\u043b\u0438\u043d\u043a\u0430
R = Q*e\/(L*pi*F*eo) =
=(3*10^-8)*(1,6*10^-19)\/(1,50*pi*4*10^-15*(8,854*10^-12)) \u043c = \n 0,02876 \u043c ~ 29 \u043c\u043c
2) \u041d\u0430 \u0441\u043a\u043e\u043b\u044c\u043a\u043e \u0438\u0437\u043c\u0435\u043d\u0438\u0442\u0441\u044f \u044d\u043d\u0435\u0440\u0433\u0438\u044f \u043f\u044b\u043b\u0438\u043d\u043a\u0438
\u043f\u043e\u0442\u0435\u043d\u0446\u0438\u0430\u043b \u043d\u0438\u0442\u0438
u1 =-2* Q\/(L*e0)*ln(R1)
u2 =-2*Q\/(L*e0)*ln(R2)
W1=q*u1
W2=q*u2
delta W = W2-W1= q*(u2-u1)=
=-2*e( -2*Q\/(L*e0)*ln(R2)+2* Q\/(L*e0)*ln(R1)) =
= 2*e*(2*Q\/(L*e0)*ln(R2)-2* Q\/(L*e0)*ln(R1)) =
=4*e*Q\/(L*e0)*(ln(R2)- ln(R1)) =
=4*e*Q\/(L*e0)*(ln(2*R1)- ln(R1)) =
=4*e*Q\/(L*e0)*ln(2 ) =
=4*(1,6*10^-19)*(3*10^-8)\/(1,5*(8,854*10^-12))*ln(2) \u0414\u0436 = \n 1,0021E-15\n \u0414\u0436
Электростатическое поле заданного распределения электрических зарядов в пустоте
1. В вершинах квадрата со стороной а находятся точечные заряды (рис. 2). Определите напряженность электростатического поля и потенциал в центре квадрата. Рассмотрите случаи, когда:
Решение. Напряженность поля и потенциал системы точечных зарядов определяются соотношениями

Учитывая, что

а) Если
б) Если
в) Если
2. Линейный заряд с плотностью у равномерно распределен вдоль нити, занимающей часть оси Z от до . Найдите выражения потенциала и напряженности электростатического поля для точек, лежащих в плоскости XY (z=0) (рис. 3).
Решение. По определению



получим


где углы показаны на рисунке.

1) Рассмотрим частный случай, когда :


2) Пусть , тогда


Найдем разность потенциалов между точками с координатами


Тогда при ,



3) При получим

Примечание. Здесь использованы интегралы

3. Очень тонкое кольцо радиуса R равномерно заряжено с линейной плотностью заряда . Вычислите потенциал и напряженность электростатического ноля в точке, лежащей на оси кольца на расстоянии z от его центра. Найдите численные значения ,
если (рис. 4).
Решение. По определению


где — радиус-вектор точки , а r — радиус-вектор элемента ; тогда для потенциала и компонент напряженности поля имеем

После интегрирования по α от 0 до 2π получим (см. также рис. 5):
Для заданных численных значений найдем

При и при



На рис. 5 отложена зависимость
4. Бесконечно длинная полоска шириной 2а заряжена поверхностным зарядом а так, что его величина зависит только от координаты, параллельной ширине полоски (рис. 6). Найдите выражения для компонент вектора напряженности электростатического поля в произвольной точке. Вычислите величину напряженности поля для случаев:
где — постоянные величины, .
Решение. Систему отсчета выберем так, как показано на рис. 6. На поверхности распределения заряда выделяем узкую полоску шириной dy параллельную оси X. Тогда заряд, приходящийся на единицу длины этой полоски, будет равен и поле созданное этой полоской в точке с координатами равно (см. решение задачи 2.):

Для компонента поля соответственно получим


В случае получим

Здесь использованы интегралы типа

В случае (б) при получим

Здесь использован интеграл

5. Две концентрические сферы с радиусами получили заряды соответственно, которые равномерно распределились по их поверхности. Найдите выражения для напряженности и потенциала электростатического поля в точке, удаленной на расстояние r от центра сфер.
Решение. Напряженность поля заряженных сфер найдем, используя теорему Остроградского—Гаусса:


Интеграл, стоящий слева, представляет собой поток вектора Е через замкнутую поверхность S. В качестве такой поверхности выберем сферу радиуса r , имеющую тот же центр, что и сферы . Из соображений симметрии следует, что во всех точках поверхности S вектор Е перпендикулярен этой поверхности и имеет одинаковую величину. Поэтому

Интеграл, стоящий справа, есть полный заряд внутри объема, ограниченного поверхностью S. Таким образом, получим


Для определения потенциала используем связь между в сферических координатах


Тогда
Постоянные определим из условий:
а) при , отсюда ;
б) при , тогда ;
в) при , тогда
Из условий (б) и (в) находим


Подставляя значения в выражения для потенциала, получим


Заметим, что нулевое значение потенциала (условие а)) можно задать для любой наперед выбранной точки. При этом изменятся только значения постоянных .
6. Бесконечно длинный круговой цилиндр радиуса R равномерно заряжен по объему с плотностью, заряда ρ . Найдите выражения для напряженности и потенциала электростатического поля в точке, удаленной на расстояние r от оси цилиндра.
Решение. Напряженность поля заряженного цилиндра найдем, используя симметрию заряда и теорему Остроградского—Гаусса:

Выберем в качестве поверхности S, через которую следует определить поток вектора Е, поверхность цилиндра радиуса r и высоты l , имеющего ту же ось, что и заданный цилиндр радиуса R . Из соображений симметрии следует, что во всех точках боковой поверхности цилиндра S вектор Е перпендикулярен этой поверхности и имеет одинаковую величину. На торцах же цилиндра S вектор Е параллелен поверхности. Поэтому
где — величина напряженности поля в точках на расстоянии r от оси цилиндра.
Для интеграла, стоящего справа, соответственно имеем

где h — радиус цилиндрического кольца объемом



Для определения потенциала используем связь между в цилиндрических координатах


Постоянные определим из условий непрерывности потенциала и равенства нулю потенциала в заданной точке, т. е.
при , отсюда ;
при , тогда .
Таким образом,
при ;
и при .
7. В каких точках на расстоянии R от диполя с моментом р величина напряженности электростатического поля будет иметь максимальное и минимальное значения (рис. 7)?

Решение. Выберем систему отсчета так, чтобы диполь находился в начале координат, а вектор р был параллелен оси Y. Из симметрии задачи следует, что во всех точках круга, полученного сечением плоскости у=const сферы радиуса R, величина Е будет одинакова. Таким образом, задача сводится к отысканию значений Е в точках круга радиуса R, лежащего в плоскости XY. По определению

Следовательно, напряженность поля в произвольной точке круга (рис. 7) равна

Исследование функции на экстремум показывает, что
при ;
а при .
8. На единицу площади очень тонкой пластинки, имеющей форму диска радиуса R, приходится n диполей ( n — постоянная величина). Считая, что все диполи обладают одинаковым дипольным моментом р, направленным перпендикулярно поверхности пластинки, найдите выражения для потенциала и напряженности электростатического поля в произвольной точке Mt расположенной на оси диска на расстоянии z от его центра (рис. 8).

Решение. Выделим на диске кольцо радиуса h и шириной dh. Тогда все диполи на поверхности этого кольца создадут в точке М одинаковый потенциал, а так как потенциал, созданный одним диполем, равен


то потенциал, созданный в точке М всеми диполями кольца ,


Напряженность поля найдем из соотношения


9. Найдите выражение для собственной энергии заряда, разномерно распределенного с плотностью р внутри сферы радиуса R. Во сколько раз энергия электростатического поля, локализованная в объеме шара, меньше энергии, локализованной вне шара?

Решение. Напряженность поля и потенциал сферы, равномерно заряженной по объему, соответственно равны

где — полный заряд внутри сферы.
Так как


10. Вычислите потенциальную энергию, приходящуюся на один заряд, расположенный в неограниченной линейной цепочке точечных зарядов, величина которых равна q , а знаки чередуются. Расстояние между соседними зарядами ±q равно а (рис. 9).

Решение. Пусть Е-энергия одного заряда, например +q, в поле остальных зарядов. Тогда собственная энергия всей системы зарядов равна (1 / 2)NE (где N — общее число зарядов). Следовательно, энергия, приходящаяся на один заряд, равна W=1/2E,
где



11. Диполь с моментом р находится на расстоянии r от точечного заряда q. Найдите выражения для энергии диполя и силы, действующей на диполь, если:
а) вектор р параллелен прямой, соединяющей заряд и диполь .
б) вектор р перпендикулярен этой прямой (рис. 10).
Решение. По определению . Так как , то для случаев
По определению . Поэтому (см. примечание):


Примечание.

При , а и при
Таким образом
12. Найдите выражения для энергии и силы взаимодействия (на единицу длины) двух равномерно заряженных, бесконечно длинных параллельных нитей с линейными плотностями заряда , находящихся на расстоянии r друг от друга (рис. 11). Какую работу (на единицу длины) нужно совершить, чтобы наполовину сблизить эти нити? Определите энергию и силу взаимодействия, а также работу, если .
Решение. Найдем, например, энергию нити с в поле нити с . Тогда





Работу найдем из условия . Тогда


Подставляя в полученные формулы значения , найдем
Читайте также:

