При каких значениях лямбда векторы 2 лямбда а имеют одинаковое направление
Советы и рекомендации по использованию лямбд Java 8 и функциональных интерфейсов.
1. Обзор
Теперь, когда Java 8 получила широкое распространение, начали появляться шаблоны и лучшие практики для некоторых из ее основных функций. В этом уроке мы подробнее рассмотрим функциональные интерфейсы и лямбда-выражения.
Дальнейшее чтение:
Почему локальные переменные, используемые в Лямбдах, должны быть окончательными или Фактически окончательными?
Java 8 – Мощное сравнение с лямбдами
2. Предпочитайте Стандартные Функциональные Интерфейсы
Функциональные интерфейсы, собранные в пакете java.util.function , удовлетворяют потребности большинства разработчиков в предоставлении целевых типов для лямбда-выражений и ссылок на методы. Каждый из этих интерфейсов является общим и абстрактным, что позволяет легко адаптировать их практически к любому лямбда-выражению. Разработчики должны изучить этот пакет, прежде чем создавать новые функциональные интерфейсы.
Рассмотрим интерфейс Foo :
и метод add() в некотором классе Use Foo , который принимает этот интерфейс в качестве параметра:
Чтобы выполнить его, вы должны написать:
Посмотрите внимательнее, и вы увидите, что Foo – это не более чем функция, которая принимает один аргумент и выдает результат. Java 8 уже предоставляет такой интерфейс в Function из пакета java.util.function .
Теперь мы можем полностью удалить интерфейс Foo и изменить наш код на:
Чтобы выполнить это, мы можем написать:
3. Используйте аннотацию @Functional Interface
Аннотируйте свои функциональные интерфейсы с помощью @Functional interface . Поначалу эта аннотация кажется бесполезной. Даже без него ваш интерфейс будет рассматриваться как функциональный, если у него есть только один абстрактный метод.
Но представьте себе большой проект с несколькими интерфейсами – трудно управлять всем вручную. Интерфейс, который был разработан, чтобы быть функциональным, может быть случайно изменен путем добавления других абстрактных методов/методов, что делает его непригодным для использования в качестве функционального интерфейса.
Но, используя аннотацию @Functional Interface , компилятор вызовет ошибку в ответ на любую попытку нарушить предопределенную структуру функционального интерфейса. Это также очень удобный инструмент для облегчения понимания архитектуры вашего приложения другими разработчиками.
Итак, используйте это:
вместо того, чтобы просто:
4. Не злоупотребляйте методами по умолчанию в Функциональных интерфейсах
Мы можем легко добавить методы по умолчанию в функциональный интерфейс. Это приемлемо для контракта функционального интерфейса до тех пор, пока существует только одно объявление абстрактного метода:
Функциональные интерфейсы могут быть расширены другими функциональными интерфейсами, если их абстрактные методы имеют одинаковую сигнатуру.
Как и в случае с обычными интерфейсами, расширение различных функциональных интерфейсов одним и тем же методом по умолчанию может быть проблематичным .
Например, давайте добавим метод default Common() в интерфейсы Bar и Baz :
В этом случае мы получим ошибку во время компиляции:
Но мы должны быть осторожны. Добавление слишком большого количества методов по умолчанию в интерфейс – не очень хорошее архитектурное решение. Это следует рассматривать как компромисс, который следует использовать только в случае необходимости для обновления существующих интерфейсов без нарушения обратной совместимости.
5. Создание Экземпляров Функциональных Интерфейсов С Помощью Лямбда-Выражений
Компилятор позволит вам использовать внутренний класс для создания экземпляра функционального интерфейса. Однако это может привести к очень подробному коду. Вы должны предпочесть лямбда-выражения:
над внутренним классом:
Подход лямбда-выражения может быть использован для любого подходящего интерфейса из старых библиотек. Он может использоваться для таких интерфейсов, как Runnable , Comparator и так далее. Однако это не означает, что вы должны пересмотреть всю свою старую кодовую базу и все изменить.
6. Избегайте Перегрузки Методов С Функциональными Интерфейсами в качестве Параметров
Используйте методы с разными именами, чтобы избежать коллизий; давайте рассмотрим пример:
На первый взгляд это кажется разумным. Но любая попытка выполнить любой из методов ProcessorImpl :
Чтобы решить эту проблему, у нас есть два варианта. Первый-использовать методы с разными именами:
Второй – выполнить кастинг вручную. Это не является предпочтительным.
7. Не рассматривайте Лямбда-выражения как внутренние классы
Несмотря на наш предыдущий пример, где мы по существу заменили внутренний класс лямбда-выражением, эти два понятия отличаются важным образом: область действия.
Когда вы используете внутренний класс, он создает новую область. Вы можете скрыть локальные переменные из заключающей области, создав новые локальные переменные с теми же именами. Вы также можете использовать ключевое слово this внутри вашего внутреннего класса в качестве ссылки на его экземпляр.
Однако лямбда-выражения работают с заключающей областью. Вы не можете скрыть переменные из заключающей области внутри тела лямбды. В этом случае ключевое слово this является ссылкой на заключающий экземпляр.
Например, в классе Use Foo у вас есть переменная экземпляра value:
Затем в каком-либо методе этого класса поместите следующий код и выполните этот метод.
Однако, пожалуйста, не используйте это правило “однострочной лямбды” в качестве догмы . Если у вас есть две или три строки в определении лямбды, может оказаться бесполезным извлекать этот код в другой метод.
8.2. Избегайте Указания Типов Параметров
Компилятор в большинстве случаев способен определить тип лямбда-параметров с помощью вывода типа . Поэтому добавление типа к параметрам является необязательным и может быть опущено.
8.3. Избегайте круглых скобок Вокруг Одного параметра
Лямбда-синтаксис требует круглых скобок только вокруг более чем одного параметра или когда параметра вообще нет. Вот почему безопасно сделать ваш код немного короче и исключить круглые скобки, когда есть только один параметр.
Итак, сделайте это:
8.4. Избегайте оператора возврата и фигурных скобок
Скобки и return операторы необязательны в однострочных лямбда-телах. Это означает, что их можно опустить для ясности и краткости.
8.5. Использование ссылок на методы
Очень часто, даже в наших предыдущих примерах, лямбда-выражения просто вызывают методы, которые уже реализованы в других местах. В этой ситуации очень полезно использовать другую функцию Java 8: ссылки на методы .
может быть заменен:
Это не всегда короче, но делает код более читабельным.
9. Используйте “Эффективно Окончательные” Переменные
Доступ к неконечной переменной внутри лямбда-выражений приведет к ошибке во время компиляции. Но это не означает, что вы должны отмечать каждую целевую переменную как окончательную.
В соответствии с концепцией ” эффективно final ” компилятор обрабатывает каждую переменную как final, до тех пор, пока она назначается только один раз.
Безопасно использовать такие переменные внутри лямбд, поскольку компилятор будет контролировать их состояние и вызывать ошибку во время компиляции сразу же после любой попытки их изменения.
Например, следующий код не будет компилироваться:
Компилятор сообщит вам, что:
Такой подход должен упростить процесс обеспечения потокобезопасности выполнения лямбды.
10. Защита переменных объекта от мутации
Одной из основных целей лямбд является использование в параллельных вычислениях, что означает, что они действительно полезны, когда речь заходит о потокобезопасности.
Парадигма “эффективного финала” здесь очень помогает, но не в каждом случае. Лямбды не могут изменить значение объекта из области охвата. Но в случае изменяемых объектных переменных состояние может быть изменено внутри лямбда-выражений.
Рассмотрим следующий код:
Этот код является законным, так как переменная total остается “фактически окончательной”. Но будет ли объект, на который он ссылается, иметь то же состояние после выполнения лямбды? Нет!
Сохраните этот пример в качестве напоминания, чтобы избежать кода, который может вызвать неожиданные мутации.
11. Заключение
В этом уроке мы рассмотрели некоторые лучшие практики и подводные камни в лямбда-выражениях и функциональных интерфейсах Java 8. Несмотря на полезность и мощь этих новых функций, они являются всего лишь инструментами. Каждый разработчик должен обращать внимание при их использовании.
Полный исходный код для примера доступен в этом проекте GitHub – это проект Maven и Eclipse, поэтому его можно импортировать и использовать как есть.
Очень часто все задаются вопросом: "Что должен показывать второй лямбда зонд ? ", "Зачем нужен второй лямбда зонд ? " и пр. А все, на самом деле, очень просто.
Второй лямбда зонд появился в результате очередного (в лохматых годах) ужесточения экологических норм, чтобы оценивать эффективность каталитического нейтрализатора (по нашему, катализатора или каталика). Он вообще не влияет на работу мотора и призван лишь отслеживать состояние каталика. Ранее вместо него был датчик температуры катализатора, который определял его забитость благодаря тому, что забитый каталик начинал сильно нагреваться проходящими выхлопными газами, в ответ на что мозг кидал ошибку по нему. Забивается вплоть до наступления перегрева каталик намного позже, чем начинает терять эффективность, поэтому отслеживать его состояние через лямбду намного эффективнее.
Сигнал второй лямбды должен быть в несколько раз ниже по значению напряжения, чем первой. Точные значения диапазонов показаний, которые ЭБУ автомобиля считает нормальными смотрите в руководстве по каждому конкретному автомобилю, но основная суть в том, что когда показания второй лямбды начинают приближаться к показаниям первой лямбды (в районе 0,500 В) или доходить до некоторого (прописанного в мозгах автомобиля) порогового значения, блок управления двигателем выкидывает ошибку по низкой эффективности каталитического нейтрализатора.
Что это означает для нас - рядовых обывателей ? Значит, что каталик ваш здох и больше вам не нужен. Свою работу он уже не выполняет, а со временем будет забиваться и ухудшать прохождение выхлопа, оплавляться или рассыпется и будет громыхать в трубе - бывает по разному. Нам нужно будет либо удалить его, заменив пламегасителем (хотя можно просто трубой, но тогда под ногами будет слышен рокот), либо забить до обострения симптомов, но, в любом случае, для погашения ошибки по лямбде, нужно будет либо поставить механическую обманку в виде проставки под лямбду, которая отодвинет ее чуток от выхлопной трубы и она будет меньше захватывать выхлоп, что уменьшит ее показания, либо сделать электронную обманку из 120 Ом-ного резистора и конденсатора на 1 - 2.2 мкф.
Собственно в этом и вся суть - ничего особенного. Ниже фото обманок.
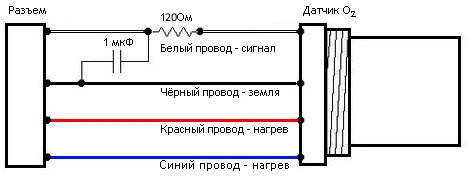
Электронная обманка

Механическая обманка

Всем привет!
Может информация кому пригодится. Когда поставил стингера, после перестановки лямбд — 1я лямбда померла. Ездил в аварийном режиме. Думал придётся покупать новую. На днях на работе сняли с диагностом обе лямбды и сравнили. Визуально они абсолютно одинаковые, обе по 4 провода и провода одного цвета. Только фишки чуть разные. Он мне перепиновал вторую лямбду на 1ю фишку и я их поменял местами. Провод 1й лямбды теперь стал нормальной длинны, не придётся наращивать. Вторая не подсоединена, просто как затычка стоит.
По диагностике 1я лямбда работает отлично, показания скачут как и должны. Теперь чек выскакивает по второй лямбде. Но она мне и не нужна, т.к. будет чиповка. Машина пошла лучше. За расходом потом посмотрю, как БК устаканится.
На днях очень резко сдох аккум. После работы стал заводить, движок еле провернул но сразу завёлся. Доехал до дома и всё, двигатель даже не проворачивался. Вынул аккум, а он вздулся. )))
Лямбда-исчисление — это формальная система в математической логике для выражения подсчетов на основе абстракции и применения функций с использованием привязки и подстановки переменных. Это универсальная модель, которую можно применять для проектирования любой машины Тьюринга. Впервые введена лямбда-исчисления Черчем, известным математиком, в 1930-х годах.
Система состоит из построения лямбда-членов и выполнения над ними операций сокращения.
Пояснения и приложения
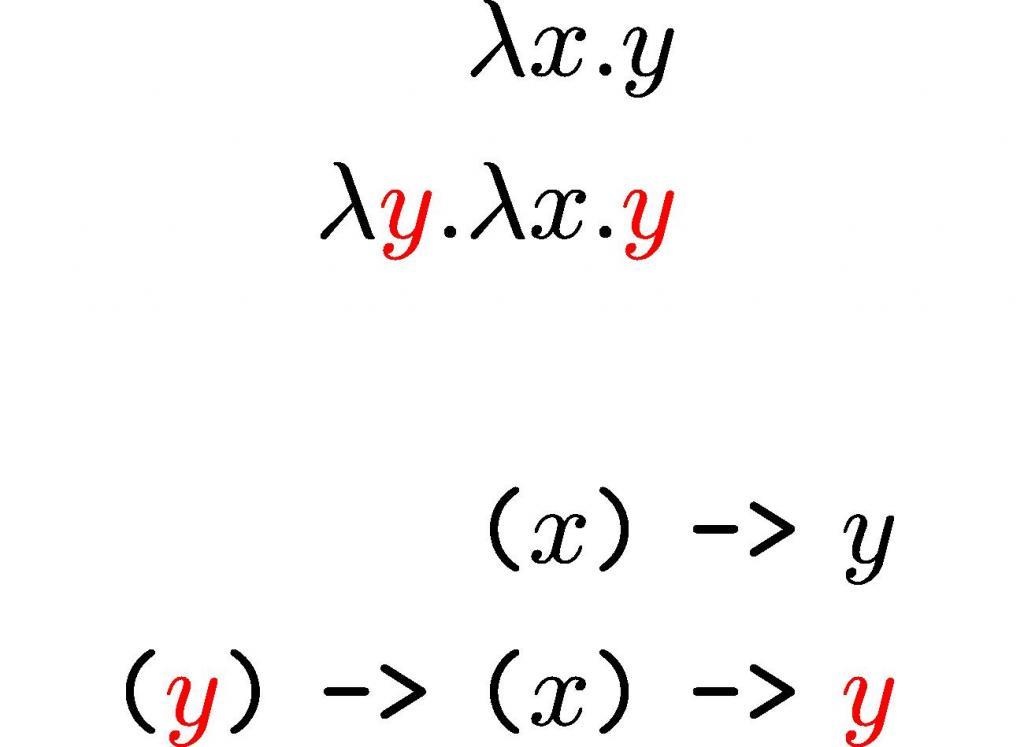
Вам будет интересно: Какие элементы входят в социальную структуру общества, виды и функции социальных групп
Греческая буква lambda (λ) используется в лямбда-выражениях и лямбда-терминах для обозначения связывания переменной в функции.
Лямбда-исчисление может быть нетипизировано или напечатано. В первом варианте функции могут быть применены только в том случае, если они способны принимать данные этого типа. Типизированные лямбда-исчисления слабее, могут выражать меньшее значение. Но, с другой стороны, они позволяют доказывать больше вещей.
Одной из причин того, что существует много разных типов — это желание ученых сделать больше, не отказываясь от возможности доказывать сильные теоремы лямбда-исчислений.
Вам будет интересно: Семейный этикет: основы и правила, особенности отношений с близкими родственниками
Система находит применение во многих различных областях математики, философии, лингвистики, и компьютерных наук. В первую очередь, лямбда-исчисления — это расчет, который сыграл важную роль в развитии теории языков программирования. Именно стили функционального создания реализуют системы. Они также являются актуальной темой исследований в теории этих категорий.
Для чайников
Лямбда-исчисление была введена математиком Алонзо Черчем в 1930-х годах в рамках исследования основ науки. Первоначальная система была показана как логически несовместимая в 1935 году, когда Стивен Клин и Дж. Б. Россер разработали парадокс Клини-Россера.
В последствии, в 1936 году Черч выделил и опубликовал только ту часть, которая имеет отношение к расчетам, то, что сейчас называется нетипизированным лямбда-исчислением. В 1940 он также представил более слабую, но логически непротиворечивую теорию, известную как система простого типа. В свое работе он объясняет всю теорию простым языком, поэтому, можно сказать, что Черч опубликовал лямбду исчисления для чайников.
Вам будет интересно: Профессии железнодорожников: перечень, описание, необходимое образование
До 1960-х годов, когда выяснилось его отношение к языкам программирования, λ стала лишь формализмом. Благодаря применениям Ричарда Монтегю и других лингвистов в семантике естественного языка, исчисление стало занимать почетное место как в лингвистике, так и в информатике.
Происхождение символа

Введение в лямбда исчисление

Система состоит из языка терминов, которые выбираются определенным формальным синтаксисом, и набора правил преобразования, которые позволяют манипулировать ими. Последний пункт можно рассматривать как эквациональную теорию или как операционное определение.
Все функции в лямбда-исчислении являются анонимными, то есть не имеющими имен. Они принимают только одну входную переменную, при этом каррирование используется для реализации графиков с несколькими непостоянными.
Лямбда-термины
Следующие три правила дают индуктивное определение, которое можно применять для построения всех синтаксически допустимых понятий:
Переменная x сама по себе является действительным лямбда-термином:
- если T это ЛТ, и x непостоянная, то (lambda xt) называется абстракцией.
- если T, а также s понятия, то (TS) называется приложением.
Ничто другое не является лямбда-термином. Таким образом, понятие действительно тогда и только тогда, когда оно может быть получено повторным применением этих трех правил. Тем не менее некоторые скобки могут быть опущены в соответствии с другими критериями.
Определение
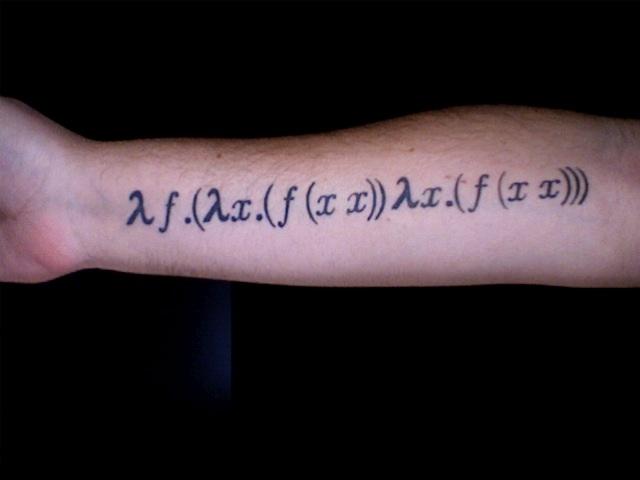
Вам будет интересно: Виды контроля качества продукции при производстве
Лямбда-выражения состоят из:
- переменных v 1, v 2. v n.
- символов абстракции 'λ' и точки '.'
- скобок ().
Множество Λ, может быть определено индуктивно:
- Если x переменная, то x ∈ Λ;
- x непостоянная и M ∈ Λ, то (λx.M) ∈ Λ;
- M, N ∈ Λ, то (MN) ∈ Λ.
Обозначение
Чтобы сохранить нотацию лямбда-выражений в незагроможденном виде, обычно применяются следующие соглашения:
- Внешние скобки опущены: MN вместо (MN).
- Предполагается, что приложения остаются ассоциативными: взамен ((MN) P) можно написать MNP.
- Тело абстракции простирается дальше вправо: λx.MN означает λx. (MN), а не (λx.M) N.
- Сокращается последовательность абстракций: λx.λy.λz.N можно λxyz.N.
Свободные и связанные переменные
Оператор λ соединяет свою непостоянную, где бы он ни находился в теле абстракции. Переменные, попадающие в область, называются связанными. В выражении λ x. М, часть λ х часто называют связующим. Как бы намекая, что переменные становятся группой с добавлением Х х к М. Все остальные неустойчивые называются свободными.
Множество свободных переменных M обозначается как FV (M) и определяется рекурсией по структуре терминов следующим образом:
- FV (x) = , где x - переменная.
- FV (λx.M) = FV (M) .
- FV (MN) = FV (M) ∪ FV (N).
Формула, которая не содержит свободных переменных, называется закрытой. Замкнутые лямбда-выражения также известны как комбинаторы и эквивалентны терминам в комбинаторной логике.
Сокращение
Значение лямбда-выражений определяется тем, как они могут быть сокращены.
Существует три вида урезания:
- α-преобразование: изменение связанных переменных (альфа).
- β-редукция: применение функций к своим аргументам (бета).
- η-преобразование: охватывает понятие экстенсиональности.
Здесь речь также идет о полученных эквивалентностях: два выражения являются β-эквивалентными, если они могут быть β-преобразованы в одно и то же составляющее, а α / η-эквивалентность определяется аналогично.
Термин redex, сокращение от приводимого оборота, относится к подтемам, которые могут быть сокращены одним из правил. Лямбда исчисление для чайников, примеры:
(λ x.M) N является бета-редексом в выражении замены N на x в M. Составляющее, к которому сводится редекс, называется его редуктом. Редукция (λ x.M) N есть M [x: = N].
Если x не является свободной в M, λ х. М х также ет-REDEX с регулятором М.
α-преобразование
Альфа-переименования позволяют изменять имена связанных переменных. Например, λ x. х может дать λ у. у. Термины, которые отличаются только альфа-преобразованием, называются α-эквивалентными. Часто при использовании лямбда-исчисления α-эквивалентные считаются взаимными.
Точные правила для альфа-преобразования не совсем тривиальны. Во-первых, при данной абстракции переименовываются только те переменные, которые связаны с одной и той же системой. Например, альфа-преобразование λ x.λ x. x может привести к λ y.λ x. х, но это может не ввергнуть к λy.λx.y Последний имеет иной смысл, чем оригинал. Это аналогично понятию программирования затенения переменных.
Во-вторых, альфа-преобразование невозможно, если оно приведет к захвату непостоянной другой абстракцией. Например, если заменить x на y в λ x.λ y. x, то можно получить λ y.λ y. у, что совсем не то же самое.
В языках программирования со статической областью видимости альфа-преобразование можно использовать для упрощения разрешения имен. При этом следя за тем, чтобы понятие переменной не маскировало обозначение в содержащей области.
В нотации индекса Де Брюйна любые два альфа-эквивалентных термина синтаксически идентичны.
Замена
Изменения, написанные Е [V: = R], представляют собой процесс замещения всех свободных вхождений переменной V в выражении Е с оборотом R. Подстановка в терминах λ определяется лямбдой исчисления рекурсии по структуре понятий следующим образом (примечание: x и y - только переменные, а M и N - любое λ-выражение).
y [x: = N] ≡ y, если x ≠ y
(M 1 M 2) [x: = N] ≡ (M 1 [x: = N]) (M 2 [x: = N])
(λ x.M) [x: = N] ≡ λ x.M
(λ y.M) [x: = N] y λ y. (M [x: = N]), если x ≠ y, при условии, что y ∉ FV (N).
Для подстановки в лямбда-абстракцию иногда необходимо α-преобразовать выражение. Например, неверно, чтобы (λ x. Y) [y: = x] приводило к (λ x. X), потому что замещенный x должен был быть свободным, но в итоге был связанным. Правильная замена в этом случае (λ z. X) с точностью до α-эквивалентности. Стоит обратить внимание, что замещение определяется однозначно с верностью до лямбды.
β-редукция
Бета-редукция отражает идею применения функции. Бета-восстановительный определяется в терминах замещения: ((X V. E) Е ') является Е [V: = Е'].
Например, предполагая некоторое кодирование 2, 7, ×, имеется следующее β-уменьшение: ((λ n. N × 2) 7) → 7 × 2.
Бета-редукция может рассматриваться как то же самое, что и концепция локальной сводимости при естественной дедукции через изоморфизм Карри – Ховарда.
η-преобразование

Эта-конверсия выражает идею экстенсиональности, которая в этом контексте заключается в том, что две функции равны тогда, когда они дают одинаковый результат для всех аргументов. Эта конвертация обменивает между λ x. (F x) и f всякий раз, когда x не кажется свободным в f.
Вам будет интересно: Откуда появились славяне: определение, описание и история
Данное действие может рассматриваться как то же самое, что и концепция локальной полноты в естественной дедукции через изоморфизм Карри – Ховарда.
Нормальные формы и слияние
Для нетипизированного лямбда-исчисления β-редукция как правило переписывания не является ни сильно нормализующей, ни слабо.
Тем не менее можно показать, что β-редукция сливается при работе до α-преобразования (т. е. можно считать две нормальные формы равными, если возможно α-преобразование одной в другую).
Поэтому и сильно нормализующие члены, и слабо налаживающие понятия имеют единственную нормальную форму. Для первых терминов любая стратегия сокращения гарантированно приведет к типичной конфигурации. Тогда как для слабо нормализующих условий некоторые стратегии сокращения могут не найти ее.
Дополнительные методы программирования

Существует большое количество идиом создания для лямбда-исчисления. Многие из них были первоначально разработаны в контексте использования систем в качестве основы для семантики языка программирования, эффективно применяя их в качестве создания низкого уровня. Поскольку некоторые стили включают лямбда-исчисление (или что-то очень похожее) в качестве фрагмента, эти методы также находят применение в практическом создании, но затем могут восприниматься как неясные или чужие.
Именованные константы
В лямбда-исчислении библиотека принимает форму набора ранее определенных функций, в которой термины являются просто конкретными константами. Чистое исчисление не имеет понятия именованных неизменных, поскольку все атомные лямбда-термины являются переменными. Но их также можно имитировать, выделив непостоянную в качестве имени константы, используя лямбда-абстракцию для связывания этой изменчивой в основной части, и применить эту абстракцию к намеченному определению. Таким образом, если использовать f для обозначения M в N, можно сказать,
Авторы часто вводят синтаксическое понятие, такое как let, чтобы разрешить писать все в более интуитивном порядке.
Заметным ограничением этого let является то, что имя f не определено в M, поскольку M находится вне области привязки лямбда-абстракции f. Это означает, что атрибут рекурсивной функции не может использоваться как M с let. Более продвинутая синтаксическая конструкция letrec, которая позволяет писать рекурсивные определения функций в этом стиле, вместо этого дополнительно использует комбинаторы с фиксированной точкой.
Печатные аналоги

Данный тип является типизированным формализмом, который использует символ для обозначения анонимной функции абстракция. В этом контексте типы обычно являются объектами синтаксической природы, которые присваиваются лямбда-терминам. Точная натура зависит от рассматриваемого исчисления. С определенной точки зрения, типизированные ЛИ можно рассматривать как уточнения нетипизированного ЛИ. Но с другой стороны, их также можно считать более фундаментальной теорией, а нетипизированное лямбда-исчисление — особым случаем только с одним типом.
Типизированные ЛИ являются основополагающими языками программирования и основой функциональных, таких как ML и Haskell. И, более косвенно, императивных стилей создания. Типизированные лямбда-исчисления играют важную роль в разработке систем типов для языков программирования. Здесь типизируемость обычно захватывает желательные свойства программы, например, она не вызовет нарушения доступа к памяти.
Типизированные лямбда-исчисления тесно связаны с математической логикой и теорией доказательств через изоморфизм Карри – Говарда, и их можно рассматривать как внутренний язык классов категорий, например, который просто является стилем декартовых замкнутых.

б)при каком значении переменной значение выражения 4у-1 равно 3у+5?
являются числа 1 и -3?
Объясните как решить, пожалуйста.
2) Найдите значение x, при котором значение дроби х/3-х меньше значения дроби 6/х на 1.
при с=1\2 , и d= 0,35.
2. Выясните при каких значениях переменной выражение
t-2\t+1
3. При каком значении переменной значение выражения 12t больше выражения 3t+5 на 4?
Вы находитесь на странице вопроса "При каких значениях λ векторы 2*λ*a и (λ^(3)-1)a имеют оодинаковое направление? а - знак вектора", категории "алгебра". Данный вопрос относится к разделу "1-4" классов. Здесь вы сможете получить ответ, а также обсудить вопрос с посетителями сайта. Автоматический умный поиск поможет найти похожие вопросы в категории "алгебра". Если ваш вопрос отличается или ответы не подходят, вы можете задать новый вопрос, воспользовавшись кнопкой в верхней части сайта.
Читайте также:

