Добротность формула что такое лямбда
Ударный спектр — это график значений максимального отклика на внешнее воздействие системы резонаторов с одной степенью свободы, упорядоченный по собственным частотам резонаторов.
Определение краткое и достаточно точное, но почему-то у людей возникают дополнительные вопросы. Дополнительные вопросы возникают оттого, что людям трудно представить себе образ даже одного резонатора с одной степенью свободы, то что говорить о целой системе.
Если объяснять этот термин на пальцах, то надо подходить к этому вопросу аккуратно и последовательно, чтобы постепенно сложить в голове человека образ описываемого явления. С материальными объектами проще — их достаточно показать, чтобы человеку всё стало ясно. С информационными явлениями гораздо сложнее, но мы эту проблему решим.
Резонатор с одной степень свободы
Представим себе объект, который может совершать колебания в пространстве только в направлении одной оси. Это и будет резонатор с одной степенью свободы. Пружины и маятники — это всё примеры резонаторов с одной степенью свободы. Хотя природа их колебаний различна в теории они описываются аналогичными уравнениями. У них есть одна собственная частота и одна резонансная частота. Для удобства практического использования эти частоты объединяют в одну, но это две разные частоты. Резонансная частота — это частота действия внешней силы, на которой достигается максимальная амплитуда колебаний. Собственная частота — это частота затухающих колебаний, когда внешняя сила исчезла и система теряет энергию, возвращаясь в положение равновесия (останавливается).

Представим себе знакомый нам всем с детства маятник — качели.
Резонансная частота маятника не зависит от массы груза (то есть не разницы кто сидит на качелях хрупкая маленькая девочка или её большой тяжёлый папа), а зависит только от длины подвеса. Чем длиннее этот подвес, тем меньше резонансная частота. Чем выше качели, тем дольше период одного качания.
Ребёнок, впервые попавший на качели, поначалу прилагает много самых разных усилий с произвольной частотой, но качели почти не двигаются. Достаточно быстро он понимает темп, в котором надо делать усилия, чтобы раскачивать качели и понимает, что делать их надо в момент, когда качели замирают на одном из пиков.
Говоря сухим научным языком, когда частота действия внешней силы совпадает с частотой резонанса система начинает в этот самый резонанс входить, увеличивая амплитуду колебаний.

Сил у ребёнка немного и раскачать качели он сильно не может. В определённый момент все силы его начинают уходит не на увеличение амплитуды колебаний, а на поддержание колебаний на том же уровне. В этот момент вся энергия, которую прикладывает ребёнок, будет тратиться за один период колебаний на преодоление трения подвеса и сопротивление воздуха. Если предположить, что в каждый период колебаний качелей ребёнок прикладывает одинаковое усилие совершая работу A, то достигнув максимальных колебаний за n раз, он затратит количество энергии:
которая перейдёт в энергию качания качелей (часть этой энергии будет рассеяна, но пока это не существенно).
После этого вся его энергия будет полностью рассеиваться за один такт качения:
После понимания этого момента можно переходит к понятию добротности.
Добротность
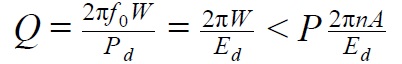
Добротность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. В общем виде для любой колебательной системы добротность вычисляется по следующей формуле:
f0 — резонансная частота;
W — запасённая энергия системы;
Pd — рассеиваемая мощность;
Ed — рассеиваемая энергия за один период колебаний;
A — работа, совершаемая внешней силой за один период колебаний;
n — количество колебаний, которое сделал система, прежде чем достигла максимальной амплитуды колебаний.
Из этой формулы можно сделать один очень важный вывод, который нам пригодится:
Чем выше добротность колебательной системы, тем больше колебаний сделает система под действием внешний силы, прежде чем достигнет максимальной амплитуды.
То есть, чем выше качели (чем длиннее маятник — тем выше его добротность) тем больше нужно сделать колебаний, чтобы их раскачать. От величины внешней силы зависит только амплитуда колебаний, которые может совершать система. Если ребёнок не сам качается на качелях, а его качает папа (а у папы силы больше и энергии он даёт больше), качели будут подниматься гораздо выше, но максимальной амплитуды качели достигнут примерно за то же число колебаний, если папа будет качать с одинаковым усилием. В качании на качелях самое главное не переусердствовать иначе ребёнка может укачать или качели сломаются.
Собственная частота
Одни колебательные системы останавливаются быстро, всего за пару тройку колебаний (большинство качелей во дворе останавливаются не более чем за 7 колебаний), а колебания других могут затухать очень долго (колокола — это тоже колебательные системы). Скорость, с которой колебания затухают, очень важный параметр. Он называется декремент затухания.
Декремент затухания
Декремент затухания или логарифмический декремент колебаний — это безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных (или через некоторое целое количество периодов) амплитуд колеблющейся величины в одну и ту же сторону:
Декремент затухания равен показателю экспоненты в законе затухающих колебаний:
Из декремента затухания можно рассчитать другую величину — коэффициент демпфирования по следующей формуле:
Коэффициент демпфирования (затухания)
Декремент затухания величина расчётная и рассчитывается по графику затухающих колебаний. Для колебательных систем с вязким трением (сила сопротивления пропорциональная скорости движения) физической величиной определяющей характер колебаний является коэффициент демпфирования .
, где
c — коэффициент силы сопротивления движению;
k — коэффициент упругости;
m — масса подвижного груза.
При коэффициенте демпфирования меньшем единицы колебательная система будет плавно затухать. Чем меньше будет коэффициент, тем дольше будут длиться колебания. При коэффициенте равном единице или большем никаких колебаний система испытывать не будет, а просто плавно будет стремиться к нулевому положению. Так, например, дверные доводчики настраивают на коэффициент демпфирования 1 и более, чтобы дверь автоматически закрылась через некоторое время без удара о створку. Демпферы для входных дверей в метро наоборот настроены на коэффициент демпфирования меньше 1. После того как человек толкнёт такую дверь она сделает два три колебания и остановится.
Коэффициент демпфирования связан с добротностью следующей формулой:
Из формулы следует, что чем больше добротность колебательной системы, тем меньше декремент затухания. Чем меньше декремент затухания, тем меньше теряется энергии с каждым колебанием и тем больше колебаний совершит система перед остановкой. Этот простой вывод нам пригодится для дальнейшей работы.
Система резонаторов
Если собрать несколько резонаторов с разными собственными частотами, но одинаковыми значениями декремента затухания, то получится та самая система резонаторов, о которой шла речь в самом начале статьи. Представьте себе площадку в парке отдыха, на которой установлены качели разных размеров, но похожие по конструкции. От размеров качелей будет зависеть собственная частота, а от конструкции и материалов декремент затухания. Таким образом, у них будут разные собственные частоты и одинаковый декремент затухания.

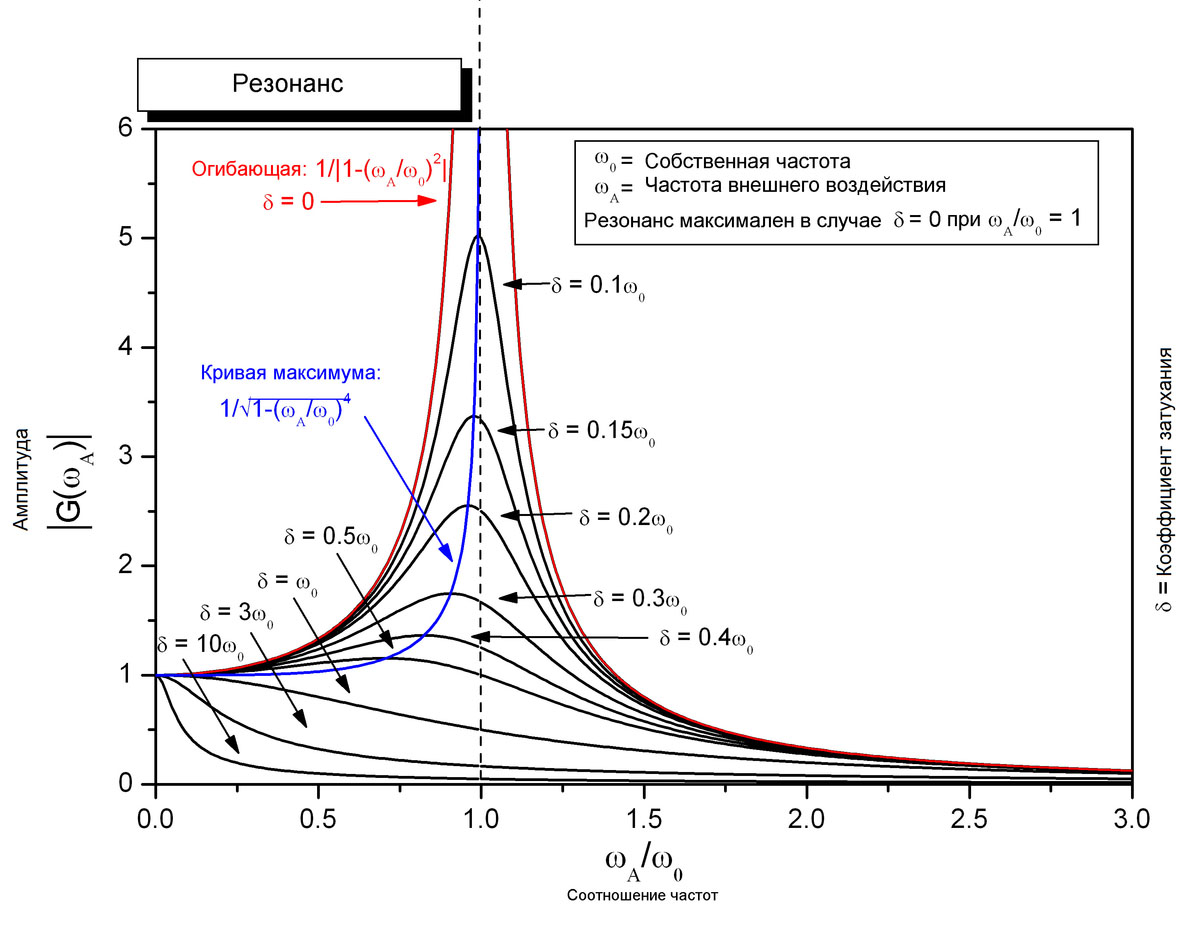
Как мы уже выяснили выше, максимальный отклик некоторых резонаторов может быть достигнут не тогда, когда мгновенное значение силы максимально, а в какой-нибудь другой момент. Этот момент зависит от гармоник, которые присутствуют в сигнале, и от их длительности. Даже если на систему действует гармонический сигнал с одной частотой, то раскачиваться под его воздействием будут все резонаторы. Максимального по амплитуде колебаний отклика достигнет резонатор с собственной частотой наиболее близкой к частоте колебаний, остальные будут колебаться меньше. Наглядно это демонстрирует график резонанса.
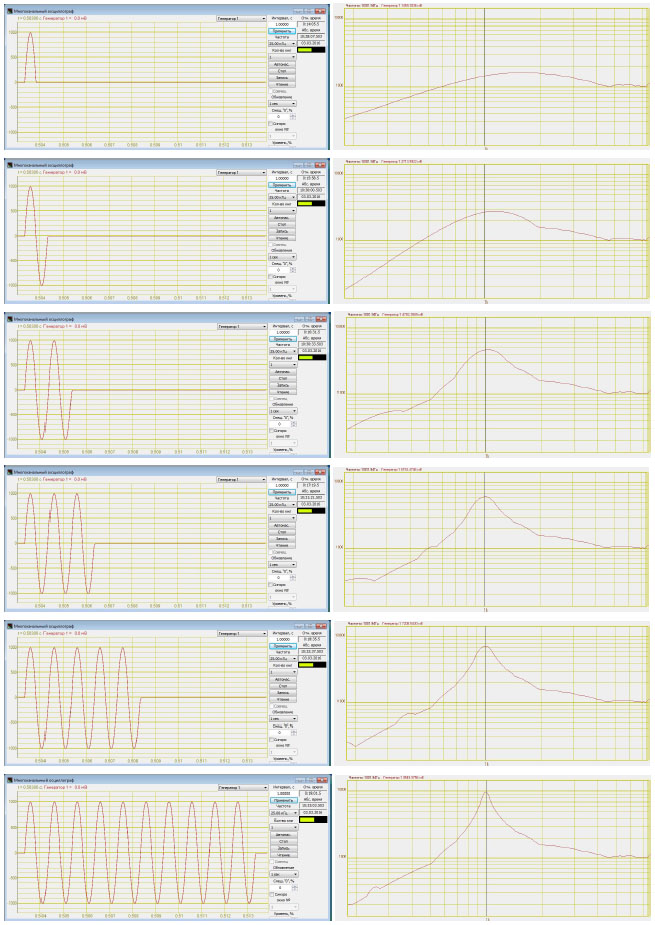
Если мы имеем дело, не с установившимися колебаниями, а с коротким воздействием, то картина будет иной. Будем на систему резонаторов действовать импульсом, состоящем из нескольких периодов синусоидального сигнала с частотой 1000 Гц от полу-периода до 10 периодов. Скажем заранее, что коэффициент демпфирования всех резонаторов равен 0,05, а добротность соответственно равна 10.
На графике резонанса изображена зависимость ответной реакции резонатора на входное воздействие постоянной амплитуды при изменяющейся частоте входного сигнала. На графике хорошо видно, что у резонаторов с низкой добротностью резонанс наступает на частоте заметно меньшей чем собственная частота резонатора. По мере роста добротности резонатора пик резонанса становится острее и выше, а частота приближается к собственной частоте резонатора.
В ударном спектре всё наоборот. Частота входного сигнала остаётся неизменной, а варьируются собственные частоты резонаторов. Добротность каждого резонатора ограничена сверху, но длительность входного воздействия позволяет раскачать все резонаторы. Поэтому добротность каждого резонатора будет определяться количеством периодов в сигнале (но не более 10).
Если частота резонатора выше частоты входного сигнала, то соотношение wa/w0 1 и амплитуда отклика быстро падает с уменьшением частоты резонатора. То есть маятники с длинным подвесом от высокочастотных воздействия даже не трогаются с места. Соответственно, большие строения (точнее сказать, строения из крупных блоков) никак не реагируют на работу отбойного молотка на улице, будь их там даже тысячи работающих одновременно.
Если взять график резонанса соответствующий δ=0.5w0, то он будет примерно соответствовать спектру ударного отклика на полу-период синуса с той лишь разницей, что он будет отражён в другую сторону. Сигналам с большим числом периодов соответствуют графики с большей добротностью. Если совместить несколько графиков ударных спектров в одних осях, то мы увидим график напоминающий график резонанса, приведённый выше, но развёрнутый в обратном направлении.
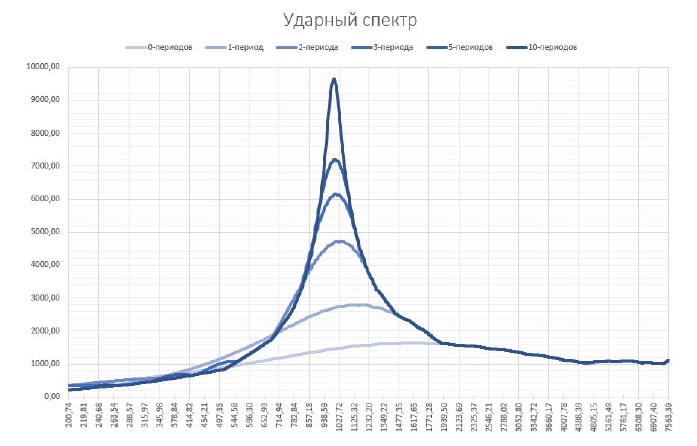
Вывод


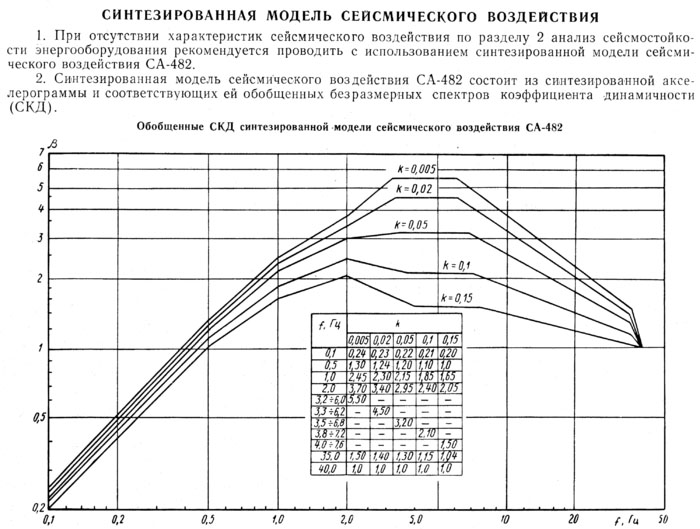
При землетрясениях наоборот измеряют ударный спектр самого землетрясения. Таким образом учёные оценивают степень разрушения зданий и сооружений [2]. Для каждого типа сооружений вычисляется диапазон наиболее разрушительных частот. Чем выше рассчитанный спектр в определённой полосе, тем больше повреждений получит здание.
При проектировании зданий в сейсмоопасных районах в конструкцию здания закладывают системы демпфирования колебаний. Системы демпфирования рассчитывают на гашение наиболее опасных частот. Такие частоты определяются исходя из анализа сейсмограмм в данной области за всё время наблюдений. И в конце проектных работы модель здания подвергают испытаниям на модельные землетрясения [3].
Колебательный контур это элементарная резонансная цепь, состоящая из конденсатора и катушки индуктивности. Бывают последовательные и параллельные колебательные контуры, в зависимости от того, как включены элементы цепи, последовательно или параллельно.
Добротность колебательного контура это величина, показывающая во сколько раз запасы энергии в контуре больше потерь энергии за один период колебаний.
Добротность колебательного контура показывает амплитуду и ширину АЧХ (амплитудно-частотной характеристики) резонанса.
Для последовательного колебательного контура добротность рассчитывается по формуле:


где R, L и C — сопротивление, индуктивность и ёмкость колебательного контура, соответственно.
Электрическая цепь, образованная последовательным соединением индуктивности L, емкости С и активного сопротивления R незначительной величины, называется колебательным контуром.
В зависимости от способа подключения к контуру ЭДС колебательный контур называется параллельным (рис. 1) или последовательным (рис. 2).
Ток в контуре зависит не только от величины подводимой к контуру ЭДС, но и от ее частоты. Эта зависимость называется резонансной характеристикой контура (рис. 3)

При некоторой частоте колебаний, подводимых к контуру, как это видно из закона Ома для полной цепи переменного тока

ток в контуре принимает максимальное значение, если

где ωL – индуктивное сопротивление;

- емкостное сопротивление;
ω – циклическая частота внешней ЭДС.
Индуктивное и емкостное сопротивление называют реактивным сопротивлением.
Если частота внешней ЭДС (ω) равна частоте собственных свободных колебаний (ω0) в колебательном контуре, то имеет место явление резонанса, а частота внешней ЭДС называется резонансной и связана с параметрами контура следующим соотношением

ω =
В случае резонанса ток в контуре принимает максимальное значение, то есть

Imax =
Качество колебательного контура определяется добротностью Q, которая является основным параметром контура. Добротностью контура называется отношение реактивной мощности к мощности потерь в контуре .
Реактивная мощность определяется формулой:

P = I 2 (ωL - ).
Мощность потерь определяется формулой:P = I 2 R.

где ωр – резонансная частота.
Как показывает теория, добротность контура может быть определена также по его резонансной характеристики (см.рис. 3).

Чтобы отобрать энергию от контура, его необходимо нагрузить, Часто нагрузкой является другой индуктивно связанный с ним контур (рис. 4).

Здесь нагрузкой является контур Lсв связи С1 и Rн, настроенный на частоту ЭДС и представляющий поэтому чисто активное сопротивление rн, так как

При нормальных условиях контур связи может отобрать половину энергии от колебательного контура.

Как известно, энергия излучения пропорциональна квадрату амплитуды тока в контуре. Для большей наглядности принято рассматривать приведенную резонансную характеристику контура, то есть не I0 от частоты, а от частоты. Поэтому ширину резонансной кривой характеризуют интервалом частот в пределах:

Откуда находим, что

График зависимости резонансной кривой от частоты изображен на рис. 5.

В работе требуется снять приведённую резонансную характеристику контура и по ней определить добротность контура. Добротность контура определяется формулой:

Однако следует помнить, что эта формула верна лишь при больших Q, то есть когда затухание собственных колебаний в контуре мало.
Порядок выполнения работы
1. Включить генератор в сеть.
2. Плавно вращая ручку оси конденсатора контура связи, найти максимальный ток по прибору и записать частоту, против которой расположена стрелка.
3. Поставить стрелку, укрепленную на оси конденсатора в левое крайнее положение.
4. Плавно меняя угол поворота конденсатора через каждые 10°, записать показания прибора в цепи катушки связи, Показания снять от 10° до 180°.

5. Зная максимальное показание прибора, подсчитать значение для каждой частоты.


Часовой пояс: UTC + 3 часа
Добротность - что же это такое?
Собственно вопрос в теме. Объясните пожалуйста популярно, что такое добротность, зачем она нужна и какие у нее свойства.
Где применяются высокодобротные контуры, а где низкодобротные.
Добротность характеризует остроту резонансного пика.
Добротность Q: Q=f0/∆f ,
где: f0 - центральная частота резонанса;
∆f - полоса пропускания по уровню 0,707 (- 3 дБ) от уровня f0, принятого за 1.
Соответственно: ниже добротность - шире полоса пропускания, резонансный пик более пологий; выше добротность - уже полоса пропускания, острее резонансный пик.
Высокая добротность нужна например, при настройке радиоприёмника на сигнал определённой радиостанции или при необходимости убрать какую-то помеху (в частности сетевой фон 50 Гц). Низкая добротность нужна в тех случаях, когда по каким-либо соображениям нет необходимости делать полосовой фильтр или же в случае необходимости работы в условиях, когда частота сигнала (помехи) слегка "плавает".
_________________
Память очень интересная штука: бывает так, что запомнишь одно, а вспомнишь другое.
JLCPCB, всего $2 за прототип печатной платы! Цвет - любой!
Несдержался.
Так-же высокая добротность очень нужна в катушке Тесла (резонанс трансформатор) Причём обоих контуров первичного и вторичного, от добротности вторичного контура напрямую зависит напряжение на выходе, первичного - КПД. Добротность обоих контуров влияет на количество незатухающих колебаний в секунду, следовательно шум катушки уменьшается и стримеры не оставляют ожеги на руках. Во как)
Сборка печатных плат от $30 + БЕСПЛАТНАЯ доставка по всему миру + трафарет
Николай2, в принципе верно.
Добротность характеризует потери в контуре на активном сопротивлении контура, проще говоря, на нагрев обмотки катушки.
Если потери велики (добротность низкая), то и колебания в контуре затухают очень быстро и для поддержания их в режиме автоколебаний нужно постоянно довольно сильно подпитывать контур внешней энергией.
При высокой добротности наоборот, потери низкие, колебания затухают гораздо медленнее и соответсвенно требуется гораздо меньш энергии для поддержания их в автоколебательном режиме.
Советую заглянуть в нашу "Обучалку" Кнопки расположены между следами Кота вверху!
_________________
Память очень интересная штука: бывает так, что запомнишь одно, а вспомнишь другое.
Рассмотрим особенности, характеристики и технологии проектирования продукции RECOM: AC/DC-преобразователи для установки на плату и для внешнего монтажа, изолированные DC/DC-преобразователи, импульсные регуляторы и силовые модули, а также средства отладки для поддержки разработчиков и ускорения выхода разработок на рынок.
Достижения компании Infineon в области силовых полупроводниковых приборов на основе кремния и карбида кремния позволяют создавать бортовые зарядные устройства с высокими значениями удельной мощности и КПД, предназначенные для электромобилей и гибридных автомобилей. В статье рассмотрены типовые схемы узлов бортовых зарядных устройств, а также приведены рекомендации по выбору элементной базы производства Infineon, которые могут быть использованы при их разработке.
Объясните пожалуйста популярно, что такое
Вопрос слишком общий и говорить можно бесконечно
Я уже говорил.
Давайте конкретную схему и в ней рассмотрим где какие катушки д.б.
Где нужны высокодобротные в разумных пределах, где достаточно и низкодобротных, а где вобще не нужна добротность.
Читайте также:

