Что показывает коэффициент лямбда в уравнении кригинга
Гридинг (griding) – это процедура перехода от неравномерного распределения точек исходных данных к равномерному, правильному в узлах сети (grid), размеры которой задаются геологом.
Цель гридинга – определение значений в узлах заданной правильной сети. Необходимые значения можно найти, используя уже имеющиеся исходные данные. Подобные процедуры называются интерполяцией.
Задачи интерполяции могут быть одномерные (данные по профилю), двумерные (карты) и трехмерные (в объеме). Все эти варианты встречаются в практике геологической разведки месторождений. Но, пожалуй, чаще всего геолог сталкивается с задачами интерполяции на плоскости, т.е. с двумерной интерполяцией.
Продемонстрируем, как с помощью системы GeoStat можно провести кригинговую интерполяцию двумерных данных.
Постановка задачи
Пусть имеются геологические данные из 15 вертикальных буровых скважин. Известны топографические координаты X и Y, а также значение параметра V (например, высота устьев скважин, или содержание определенного вещества, химического соединения, или показатель пористости). См. таблицу в формате STATISTICA ниже.

Рис. 1. Фрагмент исходных данных, выгруженных в системе GeoStat
Здесь приведены данные по содержанию меди в пробе, взятой из скважины. Кроме того, имеются координаты месторасположения скважины в некоторой системе координат.
Требуется определить значение параметра в других точках местности, например, если речь идет о высоте, тогда задача сводится к построению топографической карты поверхности участка в изолиниях.
Ниже представлены результаты анализа данных в системе GeoStat.
Визуализация исходных данных
Используя метод наименьших квадратов (меню Визуальный анализ/Карты линий уровней), интерполируем и визуализируем исходные данные с помощью трехмерных карт линий уровня (Перейдем в меню Визуальный анализ/3M карты линий уровней).

Рис. 2. Меню выбора метода визуального анализа

Рис. 3. Меню задания параметров визуального анализа
В окне задания параметров, представленном на рис. 3, пользователь указывает переменные для анализа (в данном случае это горизонтальные и вертикальные координаты, а также соответствующие им концентрации).

Рис. 4. Трехмерная карта линий уровня из отчета системы GeoStat
Из графика видно, что содержание меди в пробах увеличивается от центра области к границам.
Кроме того, заметно, что распределение содержания меди изотропно (равномерно изменяется по всем направлениям).
Для более тщательной проверки данного факта можно воспользоваться оценкой анизотропии, доступной в меню Анализа вариограмм.
Идея гридинга
Итак, интересующая нас площадь разбивается на правильные прямоугольники или квадраты. Образуется правильная, регулярная сеть, которая называется гридом. Наша задача найти значение содержания меди в пробе в узлах грида.
Пусть количество узлов – по вертикали 10 и по горизонтали 10. Всего мы должны определить значения показателя в 100 узлах и записать их в матрицу (грид-матрица).
Тем самым мы совершаем переход от 6-ти нерегулярно расположенных точек к 100 регулярно расположенным точкам в узлах грида. Определение значения содержания меди в каждом из узлов грида осуществляется выбранным методом интерполяции. А вся эта процедура перехода от нерегулярной разведочной сети к регулярной с попутным определением значений переменной в каждом узле сети называется гридингом.
Методы интерполяции
Существует довольно много методов интерполяции: скользящим средним, методы ближнего и дальнего соседа, полиномиальная регрессия, набор локальных методов интерполяции, использование радиальных базисных функций и кригинг. Данные методы доступны в меню Интерполяция системы GeoStat.
Ниже мы рассмотрим именно метод кригинга – метод интерполяции с наименьшей дисперсией.
В большинстве методов интерполяции необходимо задать диаметр поискового круга. Все точки, попавшие в поисковый круг, используются для расчета искомого значения. При этом необходимо вычислить вес каждой точки (взвешивание), другими словами, ее вклад в искомое значение. Веса в той или иной мере зависят от узла до этой точки. Разные методы интерполяции – это разные способы взвешивания исходных данных в зависимости от расстояния.
Кригинг
Кригинг является линейным методом в том смысле, что необходимое значение определяется с применением среднего взвешенного значений точек попавших в поисковый круг:
Значения мы берем из исходной таблицы.
Веса можно найти из следующего выражения:
При этом показывает ошибку кригинга – чем меньше , тем лучше сработала кригинговая процедура.
Здесь - расстояние между i-й и j-й точками, попавшими в поисковый круг.
Функция - есть экспериментальная (модельная) вариограмма. Данная функция показывает общую изменчивость в данных в зависимости от расстояния.
Вариограмма
Вариограмма, построенная для рассматриваемого примера, приведена ниже (доступна через меню Анализ вариограмм/Круговая вариограмма). Здесь мы использовали предположение изотропности изучаемого параметра. В таком случае изменчивость содержания меди одинаковая в любом направлении. Это сильно упрощает картину, т.к. можно обходиться одной координатой, точнее говоря, расстоянием между точками.

Рис. 5. Круговая вариограмма (построен коэффициент вариации)
Скажем, если требуется оценить, как сильно вариабельны данные по содержанию меди в пробах, взятых на расстоянии 30 условных единиц, то можно просто найти соответствующее значение на вариограмме. - сильная вариабельность.
Также на вариограммах по вертикали могут откладываться дисперсии – смысл от этого не меняется.
Для приведенной синей линии характерна сильная изломанность. Естественно желание заменить эту ломанную кривую какой-нибудь плавно, регулярно изменяющейся линией. Опытным путем геостатистики установили, что вариограммы могут быть подогнаны несколькими классами функций (сферические, экспоненциальные, степенные, логарифмические и др.). Они называются модельными вариограммами. Подгонка модельных вариограмм также доступна в меню Анализ вариограмм.
Результаты
Сравним результаты на картах линий уровня, построенных по исходным данным и в результате использования гридинга.

Рис. 6. Сравнение карт линии уровней в системе GeoStat
Обратите внимание, что в сетке отсутствуют некоторые узлы. Скорее всего, при расчете данных узлов ни одна точка из исходных данных не попала в соответствующий поисковый круг. Для получения информации по всем 100 узлам необходимо увеличить диаметр поискового круга. Данный тип графиков позволяет наглядно демонстрировать распределение того или иного параметра в пространстве. На графике по горизонтальным осям отложены координаты пробы, а по вертикальной – DT – акустический каротаж, измерение интервального времени пробега продольной звуковой волны. Акустический каротаж используется при структурном анализе состава недр.
В результате гридинга, поверхность стала более гладкой и адекватной, без резких всплесков по краям изучаемой области. Кроме того, получены данные по содержанию меди в 93 точках, которые были заданы геологом.
Список литературы
1. В.П.Боровиков. STATISTICA. Искусство анализа данных на компьютере: для профессионалов (2-е издание), СПб.: Питер, 2003.
2. О. Дюбрюль. Геостатистика в нефтяной геологии, Библиотека нефтяного инжиниринга.
4. В.А. Ермолов. Геология. Часть II. Разведка и геологопромышленая оценка месторождений полезных ископаемых. М: МГГУ, 2005
5. Ю.А.Капутин. Горные компьютерные технологии
Учебники и справочники
1. Справочник по прикладной статистике(под ред. Э.Ллойда, У.Ледермана). – М.: Финансы и статистика, 1990.
2. Ю.А.Розанов. Теория вероятностей, случайные процессы и математическая статистика: Учебник для вузов. – М.: Наука, 1985. – 320 с.
3. Г.И.Ивченко, Ю.И.Медведев. Математическая статистика. – М.: Высшая школа, 1984. – 248 с.
Одним из основных геостатистических методов исследования окружающей среды является метод кригинга, согласно которому оцениваемое значение регионализованной переменной величины ψр в точке p определяется как взвешенное среднее известных наблюдений в соседних точках по формуле:
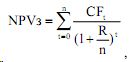
где Wi — вес i-го значения регионализованной переменной величины ψi по отношению к оцениваемой точке p из k соседних точек.
Метод кригинга предусматривает решение системы уравнений [1]:
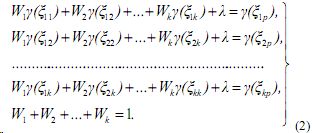
где γ(ξij) — значение полувариограммы для расстояния ξij между точками i и j; γ(ξip) — значение полувариограммы для расстояния ξip между известной точкой i и оцениваемой точкой p, λ— множитель Лагранжа.
Однако применение системы уравнений (2) нередко приводит к тому, что некоторые веса Wi оказываются либо меньше нуля, либо больше 1. В частности, такие результаты приведены Дэвисом [1]. Очевидно, это существенно искажает физический и математический смысл весов Wi и приводит к неправильной оценке величины ψp.
Подобные результаты могут быть вызваны либо неточным подбором модели полувариограммы, либо наличием среди точек наблюдений величины ψi точек, не оказывающих практического влияния на оцениваемое значение ψр. Такие точки должны иметь веса, равные нулю.
Дисперсия оценки методом кригинга может быть выражена формулой Матерона [2]:
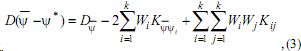
где - дисперсия ПЭС относительно ее среднего значения; - ковариация среднего значения и значения ; - ковариация значений и .
Система уравнений (2) выводится из условия минимума дисперсии в формуле (3), условия для весов Wi :
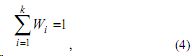
а также заменой ковариаций и соответственно на разности и .
Однако, если подставить в формулы (3) и (4) вместо Wi () и выводить систему уравнений кригинга относительно , а затем сделать обратную подстановку (Wi вместо ), то получается система уравнений кригинга
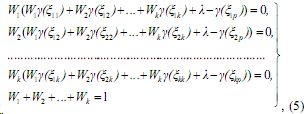
позволяющая учесть ограничения.
Так как решение системы уравнений (5) может быть затруднено из-за ее нелинейности, то для ее компьютерного решения предлагается следующий алгоритм:
Решить систему линейных уравнений (2).
Если полученное решение не отвечает ограничениям , то исключить из рассмотрения точку наблюдения с наименьшим отрицательным весом (или присвоить ему значение ноль), иначе - закончить вычисления.
Перейти после указанных изменений к пункту 1.
Полученное при реализации данного алгоритма (или использования формулы (5)) решение позволяет учесть ограничения и точнее оценить значение регионализованной переменной величины ψр.
В кригинге, как методе интерполяции, взвешивание производится, пожалуй, сложнее, чем во всех других методах. Рис. 9.17.1 частично иллюстрирует этот процесс.

Рис. 9.17.1. Схема формирования матричной системы линейных уравнений с помощью расстояний между точками и соответствующих им значений модельной вариограммы
Допустим, что в наш поисковый круг попали 3 точки 1, 2 и 3. В левом верхнем прямоугольнике показано их взаимное расположение и их положение вокруг оцениваемой точки 0 (она помечена крестом). В левом верхнем прямоугольнике точки 1, 2 и 3 соединены между собой. В правом верхнем прямоугольнике показаны те же точки, но они соединены с оцениваемой точкой О. В средней части рисунка два раза повторена сферическая модельная функция, подогнанная под экспериментальную вариограмму.
В нижней части рисунка приведено линейное матричное уравнение, в левой части которого (в колонке) стоят веса точек av а2 и а3. Их и нужно определить. Для этого нужно заполнить матрицу Yy и колонку Уог< г = 1( 2, 3>. Это делается так.
Берем расстояние от точки 1 до точки 2 и откладываем его на левой вариограмме (следите за стрелками). Значение модельной функции, соответствующее расстоянию между точками 1 и 2, заносим в два места матрицы, обозначенные у12и у21. Матрица симметричная, и эти члены матрицы равны друг другу. Точно так же поступаем со следующей парой точек. По расстоянию между точками 1 и 3 находим значение вариограммы и вставляем его на места у13 и у31. Аналогично находим и вписываем на соответствующие места значения у23 и у32. По диагонали этой матрицы стоят значения у*,. Они равны общей дисперсии изучаемой переменной у,* = о 2 .
Теперь нам остается заполнить правую колонку матричного уравнения. Сюда помещаются значения модельной вариограммы у01, у02, у03, соответствующие расстояниям между центральной точкой О и точками 1, 2 и 3. Теперь матричное уравнение решается одним из многих способов нахождения коэффициентов системы линейных уравнений. При решении способом, выбранным Ж. Матероном, появляется небольшое по величине число II — множитель Лагранжа. Чем множитель меньше, тем лучше решена система линейных уравнений.
Такова схема формирования системы уравнений для нахождения коэффициентов кригинга а(. Сама кри- гинговая оценка равна:

Здесь Zк — кригинговая интерполяционная оценка изучаемой переменной, a Z, — значения переменной в п точках, попавших в круг поиска. В нашем примере в поисковый круг попали всего 3 точки. Обычно же, на практике, в поисковый круг попадает несколько десятков окружающих проб. Соответственно и матричное уравнение расширяется до десятков строк и столбцов.
Считается, что кригинг — это интерполяционная процедура, дающая оценки с наименьшей дисперсией. Дисперсия кригинга равна:

где о 2 ^ — порог; а, — коэффициенты (веса) кри- гинга; c0i — ковариация между точкой оценивания и г-й точкой; ju— множитель Лагранжа.
Чем меньше дисперсия кригинга по сравнению с общей дисперсией, тем лучше качество полученной оценки.

Пример одномерной интерполяции данных с помощью кригинга с доверительными интервалами. Точки указывают местоположение данных. Интерполяция кригинга, показанная красным цветом, проходит по средним значениям нормально распределённых доверительных интервалов, показанных серым цветом. Пунктирная кривая показывает сплайн, который является гладким, но значительно отличается от ожидаемых промежуточных значений, задаваемых этими средними значениями.
В статистике, первоначально в геостатистике, кригинг или регрессия на основе гауссовских процессов — это метод интерполяции, для которого интерполированные значения моделируются гауссовским процессом, определяемым предыдущими ковариациями, в отличие от кусочно-полиномиального сплайна, оптимизирующего гладкость интерполируемых значений. Данный интерполяционный метод назван в честь южноафриканского горного инженера Дэниела Крига (англ.) ( рус. , занимавшегося ручным созданием геологических карт по ограниченному набору данных в некоторой области. Это вид обобщённой линейной регрессии, использующий статистические параметры для нахождения оптимальной оценки в смысле минимального среднеквадратического отклонения при построении поверхностей, кубов и карт. В основу метода положен принцип несмещённости среднего; то есть взятые все вместе значения на карте должны иметь правильное среднее значение. Глобальная несмещённость формально обеспечивается за счёт повышения низких значений и уменьшения высоких.
При правильных выбранных априорных предположениях кригинг даёт наилучшее линейное несмещённое предсказание промежуточных значений. Методы интерполяции, основанные на других критериях, таких как гладкость, не должны давать наиболее вероятных значений в промежуточных точках. Этот метод широко используется в области пространственного анализа и компьютерных (численных) экспериментах. Этот метод также известен как Wiener–Kolmogorov prediction в честь Норберта Винера и Андрея Николаевича Колмогорова.
С точки зрения общей статистики кригинг заключается в минимизации дисперсии ошибки измерения, которая является функцией от измеряемых весов. Минимизация данной дисперсии уменьшает среднюю квадратическую ошибку отклонения оцененного значения от возможного. Достигается это путём приравнивания к нулю первой производной ошибки относительно каждого неизвестного веса. В итоге выводится система уравнений, решением которой является вектор весов.
Кригинг выполняет две группы задач:
- количественное определение пространственной структуры данных,
- создание прогноза.
Количественное представление пространственной структуры данных, известное как построение вариограмм, даёт возможность пользователям подобрать к данным модель пространственной зависимости. Для расчёта (прогноза) неизвестного значения переменной в заданном месте кригинг будет использовать подходящую (подобранную) модель вариограммы, конфигурацию пространственных данных и значения в точках измерений вокруг данного местоположения.
Читайте также:

