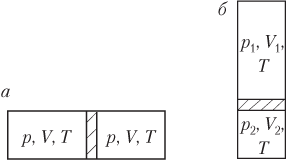закрытый с обоих концов горизонтальный цилиндр заполнен идеальным газом при температуре
§3.12. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задачи на применение газовых законов очень разнообразны. Для их решения нельзя указать какой-либо один определенный прием. Полезными могут оказаться следующие советы.
1. Если согласно условию задачи один из трех параметров (р, V или Т) постоянный, то при Т = const надо применять закон Бойля—Мариотта (3.5.2), при р = const — закон Гей-Люссака (3.7.7), а при V — const — закон Шарля (3.10.2) или (3.10.3).
Если изменяются все три параметра, то следует воспользоваться уравнением состояния в форме (3.9.9) или (3.9.5).
Уравнение состояния (3.9.9) применяется в тех случаях, когда известна масса газа и часть макроскопических параметров в определенном состоянии газа и надо найти неизвестные величины.
Для определения давления смеси газов, не вступающих в химические реакции, используют закон Дальтона (3.8.2).
Во многих задачах требуется построение графиков, изображающих разного рода процессы.
При решении большинства задач надо четко представлять себе, каково начальное состояние системы и какой процесс переводит его в конечное состояние.
Как измерить медицинским термометром температуру тела человека, если температура окружающего воздуха +42 °С?
Решение. Можно предварительно охладить термометр в холодильнике. Если холодильника нет, то нужно подержать термометр 5—8 мин под мышкой, извлечь его и сразу же стряхнуть. Термометр покажет температуру тела, так как ртуть в термометре сожмется при контакте с телом до объема, соответствующего температуре тела.
Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу т и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно р.
Решение. При горизонтальном положении цилиндра объем каждой его части обозначим через V (эти объемы равны). При вертикальном положении цилиндра объем верхней части станет равным V + AV, а нижней V
AV. Давление в нижней час- ти цилиндра станет равным + ^г . Согласно закону Бойля— Мариотта
Pl(V + AV) = + ^ у? ¦- AV) = pV.
Исключив из этих равенств ^, получим квадратное уравнение для Pl:
Второй корень квадратного уравнения отрицателен и потому лишен физического смысла.
Поршневой насос при каждом качании захватывает воздух объемом F0. При откачке этим насосом воздуха из сосуда объемом V насос совершил п качаний. Затем другой насос с тем же рабочим объемом V0 начал нагнетать воздух из атмосферы в тот же сосуд, совершив также п качаний. Какое давление установится в сосуде? Температуру воздуха во время работы насоса считать постоянной.
Решение. Согласно закону Бойля—Мариотта при откачке воздуха из сосуда после первого качания давление в сосуде
станет равным Рі = у + у , где р0— атмосферное давление. После второго качания будет выполняться равенство PlV =
= p2(V + У0) и, следовательно, р2 = р01 у + у ] , и т. д. После п
качании в сосуде установится давление рп = + у J ¦
При нагнетании воздуха в сосуд после п качаний давление станет равным
PonVo \( V Y , nVc Р -"
,РonVo \( V Лп , п"о
При любом п р > р0, так как во время нагнетания воздуха при каждом качании насос захватывает воздух, имеющий атмосферное давление р0, а при откачке при каждом качании удаляется воздух при давлении, меньшем р0.
В запаянной с обоих концов цилиндрической трубке находится воздух при нормальных условиях. Трубка разделена подвижным поршнем на две части, объемы которых V1 и V2 относятся как 1 : 2. До какой температуры t1 следует нагреть воздух в меньшей части трубки и до какой t2 охладить в большей, чтобы поршень делил трубку на две равные части, если нагревание и охлаждение в обеих частях трубки производятся
при условии j, = const?
1 1 начальных объемов у- = ^ эти объемы составляют Vl = ^ V0 и
V2 = ^ V0, где V0 — объем всей трубки. Конечные объемы обеих
частей одинаковы и равны V3 = ^ V0.
Согласно закону Гей-Люссака для воздуха в меньшей части трубки выполняется соотношение
а для воздуха в большей части
где Т0 = 273 К — температура, соответствующая начальным условиям. Отсюда
Т1 = = = 410 К, или « +137 °С; v і 1
Т2 = -у-1 = | Г0 в 205 К, или t2 = -68 °С.
В цилиндре под поршнем находится воздух при давлении Pi = 2 • 105Па и температуре = 27 °С. Определите массу т груза, который нужно положить на поршень после нагревания воздуха до температуры t2 = 50 °С, чтобы объем воздуха в цилиндре стал равен первоначальному. Площадь поршня S = 30 см2.
Решение. Так как в процессе нагревания объем воздуха в цилиндре не изменяется, то согласно закону Шарля имеем
Подставляя в (3.12.1) выражение дляр2, получим
Pi = mg Т2' Р1 + -д
Найдите среднюю (эффективную) молярную массу сухого атмосферного воздуха, предполагая известный процентный состав воздуха по массе: азот — пг = 75,52%, кислород — п2 = 23,15%, аргон — п3 = 1,28% и углекислый газ— п4 = = 0,05%.
Решение. Для каждого газа можно записать уравнение состояния:
pxV = RT, p2V = ^ RT, p3V = ^ RT, PiV = j± RT.
Здесь Mi, M2, M3 и M4 — молярные массы соответственно азота, кислорода, аргона и углекислого газа.
Складывая правые и левые части этих уравнений, получим
Для смеси газов выполняется соотношение
где m = mx + m2 + m3 + m4 — масса воздуха с объемом V, а М — искомая эффективная молярная масса.
Сравнивая уравнения состояния (3.12.2) и (3.12.3), получим М =
ТП2 + тп2 + ТПд + ТП^ ТП-у ТП2 ТП§ ТПд
м[ + м2 + м3 + Жі Разделив числитель и знаменатель на m и умножив на 100%, получим выражение для М через процентный состав воздуха по массе
м = і ? 2 і— = 28,966 • 10"3 кг/моль =
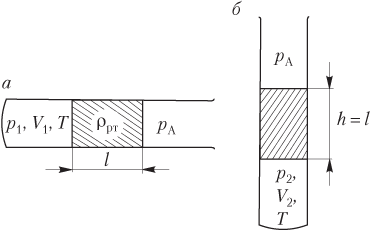
Закрытый с обоих концов цилиндр наполнен газом при давлении р — 100 кПа и температуре t = 30 °С и разделен подвижным теплонепроницаемым поршнем на две равные части длиной L по 50 см. На какую величину AT нужно повысить температуру газа в одной половине цилиндра, чтобы поршень сместился на расстояние I = 20 см, если во второй половине цилиндра температура не изменяется? Определите давление газа после смещения поршня.
Решение. Для газа в части цилиндра с постоянной температурой применим закон Бойля—Мариотта:
pLS = p1(L-l)S, (3.12.4)? где S — площадь основания цилиндра. Для нагреваемой части цилиндра запишем уравнение Клапейрона:
В уравнениях (3.12.4) и (3.12.5)— давление газа после смещения поршня, одинаковое в обеих частях цилиндра вследствие равновесия поршня, а. Т + AT в уравнении (3.12.5) — температура газа в нагретой части цилиндра.
Разделив почленно уравнение (3.12.4) на уравнение (3.12.5), получим
AT = jfri = 404 К-
Из уравнения (3.12.4) находимр^х
Сосуд объемом V = 100 л разделен пополам полупроницаемой перегородкой. В начальный момент времени в одной половине сосуда находился водород, масса которого тп1 = 2 г, а во второй — 1 моль азота. Определите давления, установившиеся по обе стороны перегородки, если она может пропус-кать только водород. Температура в обеих половинах одинакова и постоянна: t = 127 °С.
Решение. Так как водород свободно проходит через перегородку, то он распространяется по всему сосуду. Запишем уравнение Менделеева—Клапейрона для водорода после установления состояния равновесия:
3 кг/моль — молярная масса водорода.
В той части сосуда, в которой вначале был только водород, он и в дальнейшем останется в чистом виде, так что давление в этой части сосуда станет равным
Для азота уравнение Менделеева—Клапейрона имеет вид
где р2 — давление азота.
Так как в этой половине находятся водород и азот, то полное давление р согласно закону Дальтона складывается из парциальных давлений и р2, т. е.
Гелий массой 20 г, заключенный в теплоизолированном цилиндре под поршнем, медленно переводится из состояния 1 с объемом Vy = = 32 л и давлением рх = 4,1 атм в состояние 2 с объемом V2 = 9 л и давлением р2 = 15,5 атм. Какой наибольшей температуры достигнет газ при этом процессе, если на графике зависимости давления газа от объема процесс изображается прямой линией (рис. 3.18)?
Решение. Как следует из рисунка 3.18, давление и объем газа связаны линейной зависимостью: р = aV + b, где а и b — постоянные коэффициенты. Из условий задачи получаем систему уравнений
Pi = + b, р2 = aV2 + b. Решив эту систему относительно а и Ъ, найдем г / \ \ / \ / \ / \ / \ / \ / \ / \
а = ^—гт- « -0,5 атм/л, м
PlV2 „ Ъ = —Ї7—— = 20 атм. "і
V2 Подставив в уравнение Менделеева—Клапейрона вместо р выражение aV + Ъ, получим (3.12.6)
aV2 + bV= RT = const • Т. М График зависимости Т от V представляет собой параболу
(рис. 3.19). Кривая достигает максимума при Fmax = = = 20 л, когда корни квадратного уравнения (3.12.6) совпадают. При этом
Апах = + Ъ r95" style="margin:10px 5px; width: 100%;min-height:280px;">
Рис. 3.21 Уравнение (3.12.8) — это уравнение параболы, ось симметрии которой совпадает с осью Т. Следовательно, в координатах V, Т искомый график имеет вид, показанный на рисунке 3.21, а. Аналогично получим график этого процесса в координатах р, Т (рис. 3.21, б).
Вы надули щеки. При этом и давление, и объем воздуха во рту увеличиваются. Как это согласуется с законом Бойля— Мариотта?
Чтобы измерить температуру человеческого тела, приходится держать термометр под мышкой в течение 5—8 мин.
В то же время стряхнуть его можно практически сразу после измерения температуры. Почему?
Узкая вертикальная трубка длиной L, закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути длиной h. Плотность ртути равна р. Трубка расположена открытым концом вверх. Какова была длина I столбика воздуха в трубке, если при перевертывании трубки открытым концом вниз из трубки вылилась половина ртути? Атмосферное давление равно р0.
В ртутный барометр попал пузырек воздуха, вследствие чего барометр показывает давление меньше истинного. При давлении рх = 768 мм рт. ст. уровень ртути расположен на высоте hх = 748 мм, причем длина пустой части трубки I = = 80 мм. Каково атмосферное давление р2, если ртуть стоит на высоте h2 = 734 мм? Плотность ртути р = 1,36 • 104 кг/м3.
Площадь сечения цилиндра автомобильного насоса S = = 10 см2. Определите длину I цилиндра, если известно, что для накачки шины объемом V = 0,02 м3 от давления р0 = = 1 • 105Па до давления р = 3 • 105Па требуется совершить п = 100 качаний. Утечкой и нагреванием воздуха пренебречь.
В цилиндре под поршнем находится воздух. Поршень имеет форму, показанную на рисунке 3.22. Масса поршня т = 6 кг, площадь сечения цилинд-ра S = 20 см2. Атмосферное давление р0 — 105Па. Найдите массу т1 груза, который надо положить на поршень, чтобы объем Vx воздуха в цилиндре уменьшился в 2 раза. Трение не учитывать. Температура постоянна.
Газ нагрет от температуры t1 = 27 °С до температуры t2 = 39 °С. На сколько процентов увеличился его объем, если давление осталось неизменным?
Вертикальный цилиндр, закрытый подвижным поршнем, содержит газ массой т — 0,012 кг. При температуре = = 177 °С объем газа равен Vx = 4 л. При какой температуре t2 плотность этого газа будет равна р2 = 5,3 кг/м3?
Открытую стеклянную колбу, имеющую форму шара радиусом г = 2 см с горлышком длиной I = 10 см и диамет- ром d = 1 см, нагрели до температуры tlt а затем погрузили целиком в воду горлышком вниз. При охлаждении колбы вода вошла в горлышко. Когда температура колбы стала равной 12 = 13 °С, ее начали приподнимать из воды, не переворачивая, так чтобы шарообразная часть оказалась над водой, а горлышко — частично погруженным в воду. При этом, когда уровень воды в горлышке и в сосуде совпал, под водой осталась половина горлышка. Какова была температура t]_, до которой нагрели колбу?
Манометр на баллоне с газом в помещении с температурой t]_ = 17 °С показывает давление р = 240 кПа. На улице показание манометра уменьшилось на Ар = 40 кПа. Найдите температуру наружного воздуха, если атмосферное давление р0 = 100 кПа.
Два сосуда одинаковой вместимости содержат воздух, один при температуре 7\ и давлении pj, другой при температуре 2^2 и давлении р2. Сосуды соединили тонкой трубкой и после выравнивания давлений и температур воздух нагрели до температуры Т. Какое давление установится после нагревания?
Шар-зонд заполнен газом при температуре = 27 °С до давления Рх = 105 кПа. После подъема шара на высоту, где давление р0 = 80 кПа, объем шара увеличился на п = 5% и давление в нем стало отличаться от внешнего на Ар = 5 кПа. Определите температуру воздуха на этой высоте, предполагая, что газ в шаре приобрел температуру окружающего воздуха.
Из баллона со сжатым углекислым газом из-за неисправности вентиля вытекает газ. Вместимость баллона V = = 10 л. При температуре Тj = 263 К манометр показывал давление pj = 9,3 атм, а через некоторое время при температуре Т2 = 295 К манометр показывал давление р2 = = 9,4 атм. Чему равна масса тп газа, вытекшего из баллона за это время?
Газ последовательно переводится из состояния 1 с температурой Тj в состояние 2 с температурой Т2, а затем в состояние 3 с температурой Г3 и возвращается в состояние 1. Определите температуру Г3, если процессы изменения со-
стояния происходили так, как это показано на графике (рис. 3.23), а температуры и Т2 известны.
В баллоне вместимостью V — 10 л содержится водород при температуре t = 20 °С под давлением р = 107 Па. Какая масса водорода была выпущена из баллона, если при полном сгорании оставшегося газа образовалось m = 50 г во-ды?
В баллоне вместимостью V = 10 л находился гелий под давлением рх = 10 атм при температуре = 27 °С. После того как из баллона был выпущен газ массой m = 10 г, температура в баллоне была понижена до t2 = 17 °С. Определите давление гелия, оставшегося в баллоне.
Молекулярный водород некоторой массы занимает объем Vl = 1 м3 при температуре Тх = 250 К и давлении рх
= 2 • 105Па. Какое давление водород будет создавать при температуре Т2 = 5000 К и объеме V2 = 10 м3, если при столь высокой температуре молекулы водорода полностью диссоциируют на атомы?
Два сосуда объемом V1 = 200 см3 и V2 = 100 см3, наполненные кислородом при температуре t = 2 7 °С под давлением р0 — 760 мм рт. ст., соединены трубкой, внутри которой находится теплоизолирующая пористая перегородка, обеспечивающая одинаковость давлений в сосудах. Затем первый сосуд нагрели до температуры = 100 °С, а второй
охладили до температуры t2 — О °С. Определите установившееся в системе давление.
Изобразите на графиках в координатах р, V; р, Т и V, Т изотермический процесс для одного моля газа при Т =
Изобразите на графиках в координатах р, V; р, Т и V, Т изобарный процесс: 1) для р = J5j ир = 2;р1г если v = 1 моль; 2) для р = р1( если v = 3 моль.
21. На рисунке 3.24 показан график изменения состояния идеального газа в координатах р, V. Представьте этот процесс на графиках в координатах V, Тир, Т.
Тепловое расширение. Газовые законы
В два сосуда конической формы, расширяющихся кверху и книзу, и цилиндрический налита вода при температуре T = 100 °C. Как изменится давление на дно сосудов после охлаждения воды до комнатной температуры?
В сосуде конической формы, расширяющемся кверху, давление на дно увеличится. В сосуде конической формы, расширяющемся книзу, давление на дно уменьшится. В цилиндрическом сосуде давление на дно не изменится.
Две линейки — одна медная, другая железная — наложены одна на другую так, что они совпадают только одним концом. Определить длины линеек при t = 0 °C, зная, что разность их длин при любой температуре составляет Δl = 10 см. Коэффициент линейного расширения меди α1 = 17·10 -6 К -1 , железа — α2 = 12·10 -6 К -1 .
Длина медной линейки 24 см, длина железной — 34 см.
Часы, маятник которых состоит из груза малых размеров и легкой латунной нити, идут правильно при 0 °C. Найти коэффициент линейного расширения латуни, если при повышении температуры до t = +20 °C часы отстанут за сутки на 16 с.
На сколько часы будут уходить вперед за сутки при t0 = 0 °C. если они выверены при t = 20 °C, и материал, из которого сделан маятник, имеет коэффициент линейного расширения α = 0,000012 К -1 ?
При t0 = 0 °С часы спешат в сутки на τ = 20 с. При какой температуре часы будут идти точно? Коэффициент линейного расширения материала маятника α = 1,9·10 -5 К -1 .
Какую силу F надо приложить к стальному стержню сечением S = 1 см 2 , чтобы растянуть его на столько же, на сколько он удлиняется при нагревании на Δt = 1 °С? Коэффициент линейного расширения α = 12·10 -6 К -1 . Модуль Юнга E = 2,1·10 11 Н/м 2 .
Толщина биметаллической пластинки, составленной из одинаковых полосок стали и цинка, равна d = 0,1 см. Определить радиус кривизны r пластинки при повышении температуры на Δt = 11 °С. Коэффициент линейного расширения цинка α1= 25·10 -6 К -1 , а стали α2 = 12·10 -6 К -1 .
Концы стального стержня сечением S = 1 см 2 , находящегося при температуре t = 20 °С, прочно закреплены. С какой силой стержень будет действовать на опоры, если его нагреть до t1 = 200 °С? Модуль Юнга стали E = 2,0·10 11 Н/м 2 , коэффициент линейного расширения α =1,2·10 -5 К -1 ?
F = 39600 Н.
Каково давление газа p0 в электрической лампочке, объем которой V = 1 л, если при отламывании кончика последней под поверхностью воды на глубине h = 1 м в лампочку вошло m = 998,7 г воды? Атмосферное давление нормальное.
Стеклянный баллон объемом V = 1 л был наполнен испытуемым газом до давления p = 10 5 Па и взвешен. Его вес оказался равным Q = 0,9898 Н. Затем часть газа была удалена так, что давление в баллоне упало до р1 = 5·10 4 Па. Новый вес баллона оказался равным Q1 = 0,9800 Н. Какова плотность испытуемого газа при нормальном атмосферном давлении? Температура постоянна.
ρ = 2,1 кг/м 3 .
p1 = 751 мм рт. ст.
Открытую стеклянную трубку длиной l = 1 м наполовину погружают в ртуть. Затем трубку закрывают пальцем и вынимают. Какой длины столбик ртути останется в трубке? Атмосферное давление равно H = 750 мм рт. ст.
В запаянной с одного конца стеклянной трубке длиной l = 90 см находится столбик воздуха, запертый сверху столбиком ртути высотой h = 30 см; столбик ртути доходит до верхнего края трубки. Трубку осторожно переворачивают открытым концом вниз, причем часть ртути выливается. Какова высота столбика ртути, которая останется в трубке, если атмосферное давление H = 750 мм рт. ст.?
В сосуд со ртутью опускают открытую стеклянную трубку, оставляя над поверхностью конец длиной l = 60 см. Затем трубку закрывают и погружают еще на 30 см. Определить высоту столба воздуха в трубке. Атмосферное давление p0 = 760 мм рт. ст.
.
Посередине откачанной и запаянной с обоих концов горизонтальной трубки длиной L = 1 м находится столбик ртути длиной h = 20 см. Если трубку поставить вертикально, столбик ртути сместится на l = 10 см. До какого давления была откачана трубка? Плотность ртути ρ = 1,36·10 4 кг/м.
Расположенная горизонтально запаянная с обоих концов стеклянная трубка разделена столбиком ртути, на две равные части. Длина каждого столбика воздуха 20 см. Давление 750 мм рт. ст. Если трубку повернуть вертикально, ртутный столбик опускается на 2 см. Определить длину столбика ртути.
Цилиндрический сосуд делится на две части тонким подвижным поршнем. Каково будет равновесное положение поршня, когда в одну часть сосуда помещено некоторое количество кислорода, в другую — такое же по массе количество водорода, если длина сосуда l = 85 см?
В закрытом цилиндрическом сосуде с площадью основания S находится газ, разделенный поршнем массой M на два равных отсека. Масса газа под поршнем при этом в k раз больше массы газа над ним. Температуры газов одинаковы. Пренебрегая трением и массой газа по сравнению с массой поршня, найти давление газа в каждом отсеке.
; .
Имеются два мяча различных радиусов, давление воздуха в которых одинаково. Мячи прижимают друг к другу. Какой формы будет поверхность соприкосновения?
Выгнута в сторону мяча с большим радиусом.
Найти число n ходов поршня, которое надо сделать, чтобы поршневым воздушным насосом откачать воздух из сосуда емкостью V от давления p0 до давления p, если емкость насоса ΔV.
.
Упругость воздуха в сосуде равна 97 кПа. После трех ходов откачивающего поршневого насоса упругость воздуха упала до 28,7 кПа. Определить отношение объемов сосуда и цилиндра насоса.
Два баллона соединены трубкой с краном. В первом находится газ при давлении p = 10 5 Па, во втором — при p1 = 0,6·10 5 Па. Емкость первого баллона V1 = 1 л, второго — V2 = 3 л. Какое давление установится в баллонах (в мм рт. ст.), если открыть кран? Температура постоянная. Объемом трубки можно пренебречь.
Три баллона емкостями V1 = 3 л, V2 = 7 л и V3 = 5 л наполнены соответственно кислородом (p1 = 2·10 5 Па), азотом (p2 = 3·10 5 Па) и углекислым газом (p3 = 6·10 4 Па), при одной и той же температуре. Баллоны соединяют между собой, причем образуется смесь той же температуры. Каково давление смеси?
На гладком горизонтальном столе находится сосуд, разделенный перегородкой на две равные части. В одной части сосуда находится кислород, а в другой — азот. Давление азота вдвое больше давления кислорода. На сколько сдвинется сосуд, если перегородка станет проницаемой? Длина сосуда l = 20 см. Массой сосуда пренебречь. Процесс считать изотермическим.
В цилиндре, закрытом легко подвижным поршнем массой m и площадью S, находится газ. Объем газа равен V. Каким станет объем газа, если цилиндр передвигать вертикально с ускорением: а) +a; б) -a? Атмосферное давление равно p0, температура газа постоянна.
а) ; б) .
Начертить графики изотермического, изобарического и изохорического процессов в идеальном газе в координатах p, V; p, T; V, T. Объяснить, почему коэффициент объемного расширения идеальных газов равен термическому коэффициенту давления.
На рисунке изображены две изотермы одной и той же массы газа.

1. Чем отличаются состояния газов, если газы одинаковы?
2. Чем отличаются газы, если температуры газов одинаковы?
Как менялась температура идеального газа — увеличивалась или уменьшалась — при процессе, график которого в координатах p, V изображен на рисунке.

При нагревании газа получен график зависимости давления от абсолютной температуры в виде прямой, продолжение которой пересекает ось p в некоторой точке выше (ниже) начала координат. Определить, сжимался или расширялся газ во время нагревания.
На рисунке дан график изменения состояния идеального газа в координатах p, V.

Представить этот круговой процесс (цикл) в координатах p, T и V, T, обозначив соответствующие точки.
Сколько ртути войдет в стеклянный баллончик объемом 5 см 3 , нагретый до t1 = 400 °С, при его остывании до t2 = 16 °С, если плотность ртути при t = 16 °С равна ρ = 13,6 г/см 3 ?

При какой температуре находился газ, если при нагревании его на Δt = 22 °С при постоянном давлении объем удвоился? Для каких газов это возможно?
До какой температуры нужно нагреть воздух, взятый при t = 20 °С, чтобы его объем удвоился, если давление останется постоянным?
Определить, каким был бы коэффициент объемного расширения идеального газа, если бы за начальный объем его принимали объем не при t0 =0°С, а при t1 = 100 °С?
В цилиндре, площадь основания которого равна S = 100 см 2 , находится воздух при температуре t1 = 12 °С. Атмосферное давление p1 = 101 кПа. На высоте h1 = 60 см от основания цилиндра расположен поршень. На сколько опустится поршень, если на него поставить гирю массой m = 100 кг, а воздух в цилиндре при этом нагреть до t2 = 27 °С? Трение поршня о стенки цилиндра и вес самого поршня не учитывать.
Два одинаковых баллона, содержащие газ при t = 0 °С, соединены узкой горизонтальной трубкой диаметром d = 5 мм, посередине которой находится капелька ртути.

Капелька делит весь сосуд на два объема по V = 200 см 3 . На какое расстояние x переместится капелька, если один баллон нагреть на Δt = 2 °С, а другой на столько же охладить? Изменением объемов сосудов пренебречь.
Два одинаковых сосуда соединены трубкой, объемом которой можно пренебречь. Система наполнена газом и находится при абсолютной температуре T. Во сколько раз изменится давление в такой системе, если один из сосудов нагреть до абсолютной температуры T1, а другой поддерживать при прежней температуре T?
1. В горизонтально расположенном сосуде, разделенном легко подвижным поршнем, находятся с одной стороны от поршня m1 граммов кислорода, а с другой — m2 граммов водорода. Температуры газов одинаковы и равны T0. Каким будет отношение объемов, занимаемых газами, если температура водорода останется равной T0, а кислород нагреется до температуры T1?
2. Вертикально расположенный сосуд разделен на две равные части тяжелым теплонепроницаемым поршнем, который может скользить без трения. В верхней половине сосуда находится водород при температуре T и давлении p. В нижней части — кислород при температуре 2T. Сосуд перевернули. Чтобы поршень по-прежнему делил сосуд на две равные части, пришлось охладить кислород до температуры T/2. Температура водорода осталась прежней. Определить давление кислорода в первом и втором случаях.
На некоторой высоте давление воздуха p = 3·10 4 Па, а температура t = -43 0 С. Какова плотность воздуха на этой высоте?
Определить давление кислорода, масса которого m = 4 кг, заключенного в сосуд емкостью V = 2 м 3 , при температуре t = 29 °С.
Определить удельный объем азота при температуре 27 °С и давлении p = 4,9·10 4 Па.
Определить массу кислорода, заключенного в баллоне емкостью V = 10 л, если при температуре t = 13 °С манометр на баллоне показывает давление p = 9·10 6 Па.
Какова разница в массе воздуха, заполняющего помещение объемом V = 50 м 3 , зимой и летом, если летом температура помещения достигает t1 = 40 °С, а зимой падает до t2 = 0 °С? Давление нормальное.
Сколько молекул воздуха выходит из комнаты объемом V0 = 120 м 3 при повышении температуры от t1 = 15 °С до t2 = 25 °С? Атмосферное давление p0 = 10 5 Па.
Компрессор захватывает при каждом качании V0 = 4 л воздуха при атмосферном давлении p = 10 5 Па и температуре t0 = -3 °С и нагнетает его в резервуар емкостью V = 1,5 м 3 , причем температура воздуха в резервуаре держится около t1 = 45 °С. Сколько качаний должен сделать компрессор, чтобы давление в резервуаре увеличилось на Δp = 1,96·10 5 Па?
На весах установлены два одинаковых сосуда. Один заполнен сухим воздухом, другой — влажным (насыщенный водяными парами) при одинаковых давлениях и температурах. Какой из сосудов тяжелее?
По газопроводу течет углекислый газ при давлении p = 5·10 5 Па и температуре t = 17 °С. Какова скорость движения газа в трубе, если за τ = 5 мин через площадь поперечного сечения трубы S = 6 см 2 протекает m = 2,5 кг углекислого газа?
Из баллона со сжатым водородом емкостью V = 10 л вследствие неисправности вентиля утекает газ. При температуре t1 = 7 °С манометр показывал p = 5·10 6 Па. Через некоторое время при температуре t2 = 17 °С манометр показал такое же давление. Сколько утекло газа?
Какая часть газа осталась в баллоне, давление в котором было равно p = 1,2·10 7 Па, а температура t = 27 °С, если давление упало до p1 = 10 5 Па? Баллон при этом охладился до t1 = -23 °С.
До какой температуры нужно нагреть запаянный шар, содержащий m = 17,5 г воды, чтобы шар разорвался, если известно, что стенки шара выдерживают давление 10 7 Па, а объем шара V = 1 л?
В цилиндре объемом V, заполненном газом, имеется предохранительный клапан в виде маленького цилиндрика с поршнем. Поршень упирается в дно цилиндра через пружину жесткости k.

При температуре T1 поршень находится на расстоянии l от отверстия, через которое газ выпускается в атмосферу. До какой температуры T2 должен нагреться газ в цилиндре, для того чтобы клапан выпустил часть газа в атмосферу? Площадь поршня S, масса газа в цилиндре m, его молярная масса µ. Объем цилиндрика клапана пренебрежимо мал по сравнению с объемом цилиндра.
В баллоне емкостью V = 110 л помещено m1 = 0,8 кг водорода и m2 = 1,6 кг кислорода. Определить давление смеси на стенки сосуда. Температура окружающей среды t = 27 °С.
В сосуде объемом 1 л заключено m = 0,28 г азота. Азот нагрет до температуры T = 1500 °С. При этой температуре α = 30% молекул азота диссоциировано на атомы. Определить давление в сосуде.
В сосуде находится смесь азота и водорода. При температуре T, когда азот полностью диссоциирован на атомы, давление равно p (диссоциацией водорода можно пренебречь). При температуре 2T, когда оба газа полностью диссоциированы, давление в сосуде 3p. Каково отношение масс азота и водорода в смеси?
Оболочка аэростата объемом V = 1600 м 3 , находящегося на поверхности Земли, наполнена водородом на n = 7/8 при давлении p = 101 кПа и температуре t = 15 °С. Аэростат поднялся на некоторую высоту, где давление p1 = 79,3 кПа и температура t1 = 2 °С. Сколько водорода потерял аэростат при своем подъеме в результате расширения газа?
Доказать, что в атмосфере с постоянной температурой независимо от закона изменения давления с высотой подъемная сила воздушного шара с эластичной оболочкой постоянна. Газ из воздушного шара не вытекает. Пренебречь давлением, обусловленным кривизной оболочки.
Идеальный газ в конкурсных задачах
Краткая теория. Взаимодействие молекул идеального газа друг с другом происходит путём абсолютно упругих соударений. Суммарный объём молекул пренебрежимо мал по сравнению с объёмом, занимаемым газом. Идеальный газ подчиняется уравнению Клапейрона–Менделеева:
где p, V, T – соответственно давление, объём и абсолютная температура газа, m и M – масса и молярная масса газа, – универсальная (т.е. одинаковая для разных газов) газовая постоянная. Величина называется количеством вещества и выражается в молях. Эта величина, как и масса, аддитивна, т.е. суммируется. Поэтому уравнение (1) для смеси n газов примет вид
Молярная масса конкретного газа определяется по формуле , где Mr – определяемая по таблице Менделеева относительная молекулярная масса.
Закон сохранения и превращения энергии с учётом тепловых явлений – первое начало (закон) термодинамики: количество теплоты, подведённое к телу, равно изменению внутренней энергии тела плюс работе, совершаемой телом над внешними телами, т.е.
Задача 1. Два сосуда, содержащие один и тот же газ, соединены трубкой с краном. Объёмы сосудов равны V1 и V2, а давления в них p1 и p2. Каким будет давление газа после открытия крана соединительной трубки? Температура газа в обоих сосудах одинакова и не изменяется после открытия крана.
Решение. Запишем уравнение (1) для газа в обоих сосудах до открытия крана, а затем уравнение состояния газа в едином сосуде после его открытия. Эти уравнения образуют систему:
где m1 и m2 – массы газа в первом и втором сосудах соответственно. Сложив почленно первые два уравнения и сравнив получившееся уравнение с третьим, получим p(V1 + V2) = p1V1 + p2V2, откуда искомое давление
Задача показывает, что нет ничего страшного в том, что в системе уравнений неизвестных (p, m1, m2, M, T) больше, чем уравнений. Ведь от нас не требуется найти все неизвестные. Поэтому в такой ситуации не следует искать «недостающие» уравнения – их не существует.
Задача 2. Газ, масса которого равна m1, а молярная масса M1, смешали с газом, масса которого равна m2, а молярная масса M2. Найдите среднюю молярную массу смеси.
Решение. Так как количество вещества смеси газов то искомая средняя молярная масса смеси Отметим, что полученная формула легко обобщается на случай смеси n газов:
Задача 3. Трубка длиной l, открытая с обоих концов, наполовину погружена в ртуть. Трубку сверху закрывают пальцем и вынимают из ртути. Чему равна длина столбика ртути, оставшегося в трубке? Атмосферное давление уравновешивается столбом ртути высотой H.
Решение. Пусть длина столбика ртути, оставшегося в трубке, равна x. Поскольку он находится в равновесии, то сумма действующих на столбик сил равна нулю: F1 + F2 + mg = 0. Здесь mg – сила тяжести, F1 и F2 – силы давления атмосферного и разреженного воздуха над ртутью соответственно.
Из векторного равенства вытекает скалярное: F1 = F2 + mg. Так как F1 = p1S, F2 = p2S, где S – площадь сечения трубки, – плотность ртути, то имеем:
По условию, тогда В последнем уравнении два неизвестных: x и p2. Значит, нужно ещё одно уравнение. Его нам даст закон Бойля–Мариотта, записанный для воздуха в верхней половине трубки: Исключая p2 из системы уравнений
приходим к квадратному уравнению:
с двумя положительными корнями:
Какой из них выбрать? Очевидно, что
Задача 4 (мехмат МГУ, 1988). На рисунке показан цикл, совершаемый над идеальным газом, причём участок 1–2 изображает изохорный процесс, 2–3 – изобарный. Температуры газа в точках 1 и 3 равны соответственно T1 = 300 К и T3 = 400 К. Найдите температуру T2 газа в точке 2. Масса газа постоянна.
Решение. Сначала запишем уравнение для трёх вершин треугольника:
Пользуясь рисунком, меняем индексы у величин p3 и V2:
Далее исключаем неизвестную величину , которую не требуется определять:
Осталось воспользоваться несколько скрытым условием задачи: точки 0, 1, 3 лежат на одной прямой, следовательно,
Но p3 = p2, следовательно, левые части уравнений в последней системе равны. Тогда равны и правые части: откуда T2 = 346 К.
Задача 5 (МГТУ им. Н.Э.Баумана). Посередине лежащего на боку заполненного газом запаянного цилиндрического сосуда длиной L = 1 м находится тонкий поршень массой m = 0,1 кг и площадью S = 10 см 2 . Если сосуд поставить на основание, то поршень перемещается на расстояние l = 1 см. Каково было начальное давление p газа в сосуде? Трение между стенками сосуда и поршнем отсутствует.
Решение. Рассмотрим сосуд в горизонтальном и вертикальном положениях. Запишем по закону Бойля–Мариотта два уравнения, дополнив их условием механического равновесия поршня:
Выразим из первого уравнения p1, из второго – p2 и подставим эти величины в третье уравнение. В результате найдём из линейного уравнения искомое неизвестное:
Задача 6. Зимой в комнате был включён электронагреватель мощностью 1 кВт, который работал 1 ч. Найдите изменение внутренней энергии воздуха в комнате.
Решение. Окружающий нас воздух представляет собой смесь двухатомных газов, если правомерно пренебречь ничтожной примесью инертных газов. Тогда внутренняя энергия воздуха
С учётом формулы (1) Объём комнаты V = const. А что будет с давлением? Отметим, что реальное жилище – не наглухо изолированный от внешнего мира бункер. Как только включили нагреватель, давление слегка повысится по сравнению с атмосферным. Воздух через мельчайшие щёлочки начнёт выходить из комнаты. Давления внутри и вне тут же сравняются. Так что и p = const. Но тогда и U = const, следовательно, изменение внутренней энергии А нагреватель включили не для увеличения внутренней энергии воздуха, а чтобы в комнате повысилась температура!
Задача 7 (физфак МГУ, 1977). Идеальный газ медленно переводят из состояния с объёмом V1 = 32 л и давлением p1 = 4,1•10 5 Па в состояние с объёмом V2 = 9 л и давлением p2 = 15,5•10 5 Па так, что давление во время сжатия изменяется в зависимости от объёма по линейному закону p = aV + b, где a и b – постоянные величины. При каком объёме температура газа в этом процессе будет наибольшей?
Решение. Имеем систему уравнений:
из которой последовательно исключаем b и a:
Из последнего уравнения и уравнения (1) легко вывести: Зависимость температуры от объёма представляет собой квадратичную функцию с отрицательным коэффициентом (при заданных значениях p1, V1, p2, V2) при старшем члене. Значит, наибольшее значение температуры достигается при
Задача 8. Некоторую массу m идеального газа с молярной массой M нагревают под поршнем так, что его температура, изменяясь пропорционально квадрату давления, возрастает от первоначального значения T1 до T2. Определите работу, совершённую газом.
Решение. Из системы уравнений
где выражаем давление:
где k = const. Видим, что давление прямо пропорционально объёму, т.е. непостоянно. В таком случае работа определяется с помощью интеграла:
Однако для линейных функций удобнее строить их графики в системе координат (p, V) и находить работу как площадь трапеции под графиком. По формуле площади трапеции (обычной, а не криволинейной):
Задача 9 (МФТИ, 1976). В цилиндре под лёгким поршнем находится m = 14 г азота при T = 300 К. Какое количество теплоты необходимо ему сообщить при изотермическом увеличении объёма на = 4%?
Решение. По первому началу термодинамики, Но в изотермическом процессе для идеального газа U = const, откуда Значит, Q = A.
При T = const вычислить работу без интеграла, вообще говоря, нельзя. Однако, учитывая, что в первом приближении заменяем криволинейную трапецию обычной.
Интересно сравнить приведённое решение с точным решением, полученным с применением интеграла:
Разлагая натуральный логарифм в ряд: – и ограничиваясь тремя первыми членами, получим
Физика
Если идеальный газ находится в горизонтальной запаянной трубке (горизонтальном закрытом сосуде) и разделен на две части легкоподвижной перегородкой, то уравнение состояния следует записывать для левой и правой частей трубки по отдельности.
Для идеального газа (газов), находящегося в горизонтальной запаянной трубке, разделенной легкоподвижной перегородкой:
- давление газа (газов) в обеих частях трубки одинаково в тот момент, когда перегородка неподвижна:
p 1 = p 2 = p = const;
- остальные параметры газа (газов) могут отличаться.
Пусть слева и справа от перегородки (рис. 5.10) находятся разные идеальные газы при разной температуре. В тот момент, когда перегородка покоится, уравнения Менделеева — Клапейрона записываются для них в виде системы:
p V 1 = ν 1 R T 1 , p V 2 = ν 2 R T 2 , >
где p , V 1 , ν 1 , T 1 — давление, объем, количество вещества и температура газа, находящегося в левой части трубки; p , V 2 , ν 2 , T 2 — давление, объем, количество вещества и температура газа, находящегося в правой части трубки; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
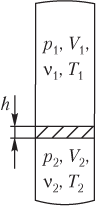
Уравнение состояния для газа в вертикальной запаянной трубке
Если идеальный газ находится в вертикальной запаянной трубке и разделен на две части легкоподвижной перегородкой, то уравнение состояния следует записывать для верхней и нижней частей трубки, дополняя систему выражением для давления, которое оказывает перегородка на нижнюю часть газа.
Для идеального газа (газов), находящегося в вертикальной запаянной трубке, разделенной горизонтальной легкоподвижной перегородкой:
- давление газа (газов) в верхней и нижней частях трубки различно
- остальные параметры газа (газов) также могут отличаться.
Давления газа в верхней и нижней частях трубки связаны между собой соотношением
где p 2 — давление газа в нижней части трубки; p 1 — давление газа в верхней части трубки; p 0 — давление перегородки на газ, находящийся в нижней части трубки.
Пусть сверху и снизу от перегородки (рис. 5.11) находится идеальный газ при разной температуре; тогда уравнения Менделеева — Клапейрона записываются для него в виде системы:
p 1 V 1 = ν 1 R T 1 , p 2 V 2 = ν 2 R T 2 , >
где p 1 , V 1 , ν 1 , T 1 — давление, объем, количество вещества и температура газа, находящегося в верхней части трубки; p 2 , V 2 , ν 2 , T 2 — давление, объем, количество вещества (газа) и температура газа, находящегося в нижней части трубки; R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К).
Давление перегородки на газ, находящийся в нижней части запаянной вертикальной трубки, может рассчитываться по двум различным формулам:
p 0 = m g S или p 0 = ρ gh ,
где m — масса перегородки; g — модуль ускорения свободного падения; S — площадь сечения трубки; ρ — плотность вещества перегородки (используется в том случае, когда перегородкой является столбик жидкости высотой h ).
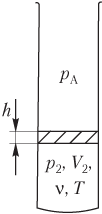
Уравнение состояния для газа в трубке, запаянной с одной стороны
Если идеальный газ находится в вертикальной , открытой с одного конца трубке и отделен от атмосферы легкоподвижной перегородкой, находящейся в равновесии, то существует соотношение, связывающее давление газа с атмосферным. Вид формулы зависит от того, какой из концов трубки является открытым.
Пусть идеальный газ находится в нижней части вертикальной трубки с открытым верхним концом и отделен от атмосферы легкоподвижной перегородкой (рис. 5.12).
Тогда давление газа в трубке связано с атмосферным давлением формулой
где p A — атмосферное давление; p 2 — давление газа в нижней части трубки; р 0 — давление перегородки на газ, находящийся в нижней части трубки, рассчитывается по одной из формул:
p 0 = m g S или p 0 = ρ gh ,
где m — масса перегородки; g — модуль ускорения свободного падения; S — площадь сечения трубки; ρ — плотность вещества перегородки; h — высота перегородки.
Уравнение Менделеева — Клапейрона записывается только для газа, находящегося в нижней части трубки:
где V 2 — объем, занимаемый газом; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); T — температура газа.
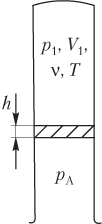
Пусть идеальный газ находится в верхней части вертикальной трубки с открытым нижним концом и отделен от атмосферы легкоподвижной перегородкой (рис. 5.13). Тогда давление газа в трубке связано с атмосферным давлением формулой
где p 1 — давление газа в верхней части трубки; p A — атмосферное давление; p 0 — давление перегородки на столб воздуха, находящегося снаружи трубки, рассчитывается по одной из формул
p 0 = m g S или p 0 = ρ gh .
Уравнение Менделеева — Клапейрона записывается только для газа, находящегося в верхней части трубки:
где V 1 — объем, занимаемый газом; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); T — температура газа.
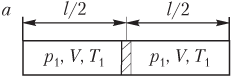
Пример 22. Закрытый цилиндр длиной 110 см, расположенный горизонтально, разделен легкоподвижным поршнем на две равные части. В обеих частях цилиндра находится один и тот же газ при температуре 300 К. На сколько градусов нужно нагреть газ в одной из частей цилиндра для того, чтобы поршень сместился на 50 мм?
Решение . Количество газа ν в левой и правой частях цилиндра одинаково. Рисунок иллюстрирует условие задачи:
- поршень находится посередине цилиндра (рис. а ) — газ в обеих частях цилиндра характеризуется параметрами p 1 , V , T 1 ; давление газа по обе стороны от поршня одинаково: p 1 = const;
- поршень смещается влево при повышении температуры газа в правой части цилиндра (рис. б ) — газ слева от поршня характеризуется параметрами p 2 , V 1 , T 1 , а справа — параметрами p 2 , V 2 , T 2 ; давление газа по обе стороны от поршня также одинаково: p 2 = const.
Запишем уравнение Менделеева — Клапейрона для трех состояний газа, показанных на рисунке:
p 1 V = ν R T 1 , p 2 V 1 = ν R T 1 , p 2 V 2 = ν R T 2 , >
где V , V 1 , V 2 — объемы газа в указанных состояниях, V = Sl /2, V 1 = Sl 1 , V 2 = Sl 2 ; S — площадь поперечного сечения сосуда; l /2, l 1 , l 2 — расстояния, показанные на рисунке; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Искомой величиной является разность температур:
определяемая разностью третьего и второго уравнений:
p 2 ( V 2 − V 1 ) = ν R ( T 2 − T 1 ).
Деление записанного уравнения на первое уравнение системы дает
p 2 ( V 2 − V 1 ) p 1 V = ν R ( T 2 − T 1 ) ν R T 1 ,
а с учетом явного вида объемов искомая разность температур определяется формулой
Δ T = p 2 T 1 p 1 ⋅ ( V 2 − V 1 ) V = p 2 T 1 p 1 ⋅ l 2 − l 1 l / 2 .
Отношение давлений найдем делением первых двух уравнений системы:
p 2 V 1 p 1 V = ν R T 1 ν R T 1 = 1 , т.е. p 2 p 1 = V V 1 = l / 2 l 1 .
Подстановка в выражение для разности температур дает
Δ T = T 1 ⋅ l / 2 l 1 ⋅ l 2 − l 1 l / 2 = T 1 ⋅ l 2 − l 1 l 1 = T 1 ⋅ ( l 2 l 1 − 1 ) .
Расстояния, входящие в формулу, определяются следующим образом:
l 1 = l / 2 − Δ l , l 2 = l / 2 + Δ l , >
где ∆ l — смещение поршня.
Тогда искомая разность температур определяется формулой
Δ T = T 1 ⋅ ( l / 2 + Δ l l / 2 − Δ l − 1 )
Δ T = 300 ⋅ ( 110 ⋅ 10 − 2 / 2 + 50 ⋅ 10 − 3 110 ⋅ 10 − 2 / 2 − 50 ⋅ 10 − 3 − 1 ) = 60 К = 60 °С.
Нагревание газа в правой части цилиндра на 60 °С приводит к смещению поршня влево на указанное расстояние.
Пример 23. Найти давление газа в горизонтальной запаянной трубке сечением 50 мм 2 , разделенной столбиком ртути массой 12 г на два объема по 60 см 3 , если при повороте трубки в вертикальное положение нижний объем равен 30 см 3 . Температура газа при повороте трубки не изменяется.
Решение . Количество газа ν в обеих частях трубки одинаково. Рисунок иллюстрирует условие задачи:
- столбик ртути находится посередине трубки (рис. а ) — газ в обеих частях трубки характеризуется параметрами p , V , T ; давление газа по обе стороны от столбика ртути одинаково: p = const;
- столбик ртути смещается вниз при повороте трубки в вертикальное положение (рис. б ) — газ в верхней части трубки характеризуется параметрами p 1 , V 1 , T , а в нижней части трубки — параметрами p 2 , V 2 , T ; давления газа в верхней и нижней части трубки связаны соотношением
где p 0 — давление столбика ртути на газ, находящийся в нижней части трубки —
где m — масса столбика ртути; g — ускорение свободного падения; S — площадь поперечного сечения сосуда;
Запишем уравнение Менделеева — Клапейрона для трех состояний газа, показанных на рисунке:
p V = ν R T , p 1 V 1 = ν R T , p 2 V 2 = ν R T , >
где R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Деление первого уравнения на второе позволяет выразить давление газа в верхней части трубки через давление газа в трубке, находящейся в горизонтальном положении:
p V p 1 V 1 = ν R T ν R T , т.е. p 1 = p V V 1 .
Делением первого уравнения на третье выразим давление газа в нижней части трубки через давление газа в трубке, находящейся в горизонтальном положении:
p V p 2 V 2 = ν R T ν R T , т.е. p 2 = p V V 2 .
Подстановка полученных выражений в формулу, связывающую давления газа в верхней и нижней частях трубки, дает
p V V 2 = p V V 1 + p 0 , или p = p 0 V 1 V 2 V ( V 1 − V 2 ) .
Найдем объем V 1 , считая объемы V и V 2 известными:
V = 60 см 3 , V 2 = 30 см 3 .
V 1 = 2 V − V 2 = 2 ⋅ 60 − 30 = 90 см 3 .
Давление газа в горизонтальной трубке определяется формулой
p = p 0 90 ⋅ 30 60 ⋅ ( 90 − 30 ) = 0,75 p 0 = 0,75 m g S .
p = 0,75 ⋅ 12 ⋅ 10 − 3 ⋅ 10 50 ⋅ 10 − 6 = 1,8 ⋅ 10 3 Па = 1,8 кПа.
Следовательно, давление газа в горизонтальной трубке было равно 1,8 кПа.
Пример 24. Газ, находящийся в горизонтальной трубке, запаянной с одного конца, заперт столбиком ртути плотностью 13,6 г/см 3 . Объем газа составляет 240 см 3 , а длина столбика ртути — 150 мм. При повороте трубки в вертикальное положение открытым концом вверх, объем газа становится равным 200 см 3 . Найти атмосферное давление.
Решение . Рисунок иллюстрирует условие задачи:
- трубка расположена горизонтально (рис. а ) — давление газа p 1 равно атмосферному давлению p A :
объем газа, запертого столбиком ртути, равен значению, указанному в условии задачи:
- трубка расположена вертикально (открытым концом вверх) (рис. б ) — давление газа в нижней части равно сумме давлений:
p 2 = p A + ρ рт gh ,
где ρ рт — плотность ртути; g — модуль ускорения свободного падения; h — длина столбика ртути, h = l ;
объем газа в нижней части трубки
количество газа и его температура при повороте трубки не изменяются:
ν = const, T = const.
Запишем уравнения Менделеева — Клапейрона для двух состояний газа в следующем виде:
- трубка расположена горизонтально —
где p 1 , V 1 — давление и объем газа, запертого столбиком ртути, при горизонтальном положении трубки; ν — количество газа, запертого столбиком ртути; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К);
- трубка расположена вертикально —
где p 2 , V 2 — давление и объем газа, запертого столбиком ртути, при вертикальном положении трубки.
Равенство правых частей уравнений состояния газа позволяет записать:
p 1 V 1 = p 2 V 2 ,
или, в явном виде, —
p A V 1 = ( p A + ρ рт gh ) V 2 .
Отсюда следует, что искомое атмосферное давление определяется формулой
p A = ρ рт g h V 2 V 1 − V 2 .
Расчет дает величину
p A = 13,6 ⋅ 10 3 ⋅ 10 ⋅ 150 ⋅ 10 − 3 ⋅ 200 ⋅ 10 − 6 240 ⋅ 10 − 6 − 200 ⋅ 10 − 6 = 102 ⋅ 10 3 Па = 102 кПа.
Следовательно, атмосферное давление составляет 102 кПа.
Пример 25. Газ, находящийся в горизонтальной трубке, запаянной с одного конца, заперт столбиком ртути плотностью 13,6 г/см 3 . Объем газа составляет 208 см 3 , а длина столбика ртути — 150 мм. При повороте трубки в вертикальное положение открытым концом вниз, объем газа становится равным 260 см 3 . Найти атмосферное давление.
Решение . Рисунок иллюстрирует условие задачи:
- трубка расположена горизонтально ( а ) — давление газа p 1 равно атмосферному давлению p A :
объем газа, запертого столбиком ртути, равен значению, указанному в условии задачи:
- трубка расположена вертикально (открытым концом вниз) ( б ) — давление газа в нижней части равно сумме давлений:
p A = p 2 + ρ рт gh ,
где ρ рт — плотность ртути; g — модуль ускорения свободного падения; h — длина столбика ртути, h = l ;
объем газа в нижней части трубки:
количество газа и его температура при повороте трубки не изменяются:
ν = const, T = const.
Запишем уравнения Менделеева — Клапейрона для двух состояний газа в следующем виде:
- трубка расположена горизонтально —
- трубка расположена вертикально —
где R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К)
Равенство правых частей уравнений состояния газа позволяет записать:
p 1 V 1 = p 2 V 2 ,
или, в явном виде, —
p A V 1 = ( p A − ρ рт gh ) V 2 .
Отсюда следует, что искомое атмосферное давление определяется формулой
p A = ρ рт g h V 2 V 2 − V 1 .
Расчет дает величину
p A = 13,6 ⋅ 10 3 ⋅ 10 ⋅ 150 ⋅ 10 − 3 ⋅ 260 ⋅ 10 − 6 260 ⋅ 10 − 6 − 208 ⋅ 10 − 6 = 102 ⋅ 10 3 Па = 102 кПа.
Читайте также: