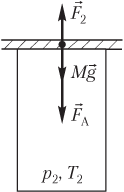в цилиндре под поршнем при постоянной температуре находится газ объем v газа при давлении
11. МКТ и Термодинамика (объяснение явлений)
На рисунке показана зависимость давления газа \(p\) от его плотности \(\rho\) в циклическом процессе, совершаемом 2 моль идеального газа в идеальном тепловом двигателе. Цикл состоит из двух отрезков прямых и четверти окружности.

На основании анализа этого циклического процесса выберите два верных утверждения.
1) В процессе 1−2 температура газа уменьшается.
2) В состоянии 3 температура газа максимальна.
3) В процессе 2−3 объём газа уменьшается.
4) Отношение максимальной температуры к минимальной температуре в цикле равно 8.
5) Работа газа в процессе 3−1 положительна.
1) По уравнению Клапейрона – Менделеева: \[p=\dfrac<\rho><\mu>RT,\] где \(T\) – температура, \(\mu\) – молярная масса газа.
Давление уменьшилось в 4 раза, а плотность увеличилась в 2 раза, следовательно, температура уменьшилась в 8 раз.
Утверждение 1 – \(\color
2) Аналогично предыдущему пункту \[p=\dfrac<\rho><\mu>RT\] Максимальная температура будет в состоянии 1 (давление максимально, плотность минимальна)
Утверждение 2 – \(\color
3) В процессе 2 – 3 плотность меньшается, а по формуле: \[\rho =\dfrac
Утверждение 3 – \(\color
4) Аналогично пункту 2, минимальность температуры будет достигнута в точке с наименьшим давлением и наибольшей плотностью (т. 2), а отношение температур действительно равно 8
Утверждение 4 – \(\color
5) В процессе 2 – 3 плотность постоянна, следовательно, объем постоянен и газ не совершает работу.
Утверждение 5 – \(\color
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В начальный момент времени в левой части сосуда содержится 4 моль гелия, в правой – 40 г аргона. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул аргона. Температура газов одинаковая и остаётся постоянной. Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Концентрация гелия в правой части сосуда в 2 раза меньше, чем аргона.
2) Отношение давления газов в правой части сосуда к давлению газа в левой части равно 1,5.
3) В правой части сосуда общее число молекул газов меньше, чем в левой части.
4) Внутренняя энергия гелия и аргона одинакова.
5) В результате установления равновесия давление в правой части сосуда увеличилось в 3 раза.
Перегородка проницаема только для молекул гелия, поэтому в результате установления равновесия парциальное давление гелия в левой части будет равно парциальному давлению гелия в правой части. Давление газа можно вычислить по формуле: \[p=\dfrac<\nu R T>
Найдём связь концентрации и количества вещества: \[n=\dfrac
Используя полученное выше, рассмотрим данные в задании утверждения.
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
1) \(\color
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
2) \(\color
Отношение давлений: \[\dfrac
3) \(\color
Количество вещества газов в правой части сосуда больше количества вещества газа в левой части сосуда, следовательно, в правой части сосуда общее число молекул газа больше, чем в левой части сосуда.
4) \(\color
Внутренняя энергия одноатомного идеального газа может быть вычислена по формуле: \[U=\dfrac<3><2>\nu R T\] Температура газов одинакова. Количество вещества гелия больше количества вещества аргона, следовательно, внутренняя энергия гелия больше внутренней энергии аргона.
5) \(\color
айдём отношение конечного давления в правой части сосуда к начальному давлению в правой части сосуда: \[\dfrac
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). Газ нагревают.
Выберите из предложенного перечня два верных утверждения, верно описывающие данный процесс, и укажите их номера.
1) Объём газа в этом процессе остаётся неизменным.
2) Давление газа в сосуде остаётся неизменным.
3) Плотность газа в этом процессе увеличивается.
4) Сила Архимеда, действующая на шарик, уменьшается.
5) Концентрация молекул газа в сосуде увеличивается.
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлениии.
Уравнение состояния газа: \[pV=\nu RT\] где \(\nu\) — количество вещества, \(T\) — температура в Кельвинах, \(p\) — давление газа, \(V\) — объем, занимаемый газом, \(R\) — универсальная газовая постоянная. Выразим объем \[V=\dfrac<\nu RT>
\] При нагревании газа объем увеличивается.
Утверждение 1 — \(\color
3) Плотность газа: \[\rho=\dfrac
Утверждение 3 — \(\color
4) Сила Архимеда: \[F_<\text<Арх>>=\rho gV\] где \(\rho\) — плотность газа, \(V\) — объем шарика, \(g\) — ускорение свободного падения. Плотность уменьшается, значит, сила Архимеда уменьшается.
Утверждение 4 — \(\color
5) Концентрация: \[n=\dfrac
Утверждение 5 — \(\color
Физика
Для идеального газа, находящегося в сосуде под поршнем , необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
- постоянным остается также количество вещества (газа):
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
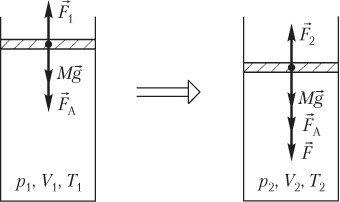
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F → (рис. 5.9).
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p 1 V 1 = ν R T 1 , p 2 V 2 = ν R T 2 , >
где p 1 , V 1 , T 1 — давление, объем и температура газа в начальном состоянии; p 2 , V 2 , T 2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
M g + F A = F 1 , M g + F A + F = F 2 , >
где M — масса поршня; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; S — площадь сечения поршня; F 1 — модуль силы давления газа на поршень в начале процесса, F 1 = p 1 S ; p 1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F 2 — модуль силы давления газа на поршень в конце процесса, F 2 = p 2 S ; p 2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
- если процесс происходит медленно, то температура газа остается постоянной –
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня , закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
- в остальных случаях поршень обладает определенной ненулевой массой —
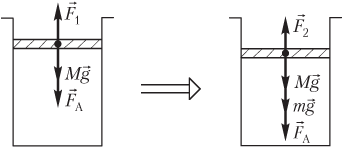
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм 2 и массой 1,80 кг находится 360 см 3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см 3 . Температура газа при его сжатии не изменяется. Определить массу гирь.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 1 , действующая со стороны газа (до его сжатия);
- сила давления газа F → 2 , действующая со стороны газа (после его сжатия);
- m g → — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
где F 1 — модуль силы давления газа, F 1 = p 1 S ; p 1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F 2 = Mg + F A + mg ,
где F 2 — модуль силы давления газа, F 2 = p 2 S ; p 2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
где V 1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
где V 2 — объем сжатого поршнем газа.
p 1 V 1 = p 2 V 2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p 1 S = M g + p A S , p 2 S = M g + p A S + m g , p 1 V 1 = p 2 V 2 , >
которую требуется решить относительно массы гирь m .
Для этого выразим отношение давлений p 2 / p 1 из первой пары уравнений:
p 2 p 1 = M g + p A S + m g M g + p A S
и из третьего уравнения:
p 2 p 1 = V 1 V 2 ,
запишем равенство правых частей полученных отношений:
M g + p A S + m g M g + p A S = V 1 V 2 .
Отсюда следует, что искомая масса определяется формулой
m = ( M + p A S g ) ( V 1 V 2 − 1 ) .
Вычисление дает результат:
m = ( 1,80 + 100 ⋅ 10 3 ⋅ 250 ⋅ 10 − 6 10 ) ( 360 ⋅ 10 − 6 240 ⋅ 10 − 6 − 1 ) = 2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см 2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение . На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → 2 , действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
где F 2 — модуль силы давления нагретого газа, F 2 = p 2 S ; p 2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F A — модуль силы атмосферного давления, F A = p A S ; p A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
где p 1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p 1 = p A ; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
где p 2 — давление нагретого газа; T 2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
p A V = ν R T 1 , p 2 V = ν R T 2 , p 2 S = M g + p A S ; >
систему необходимо решить относительно температуры T 2 , до которой следует нагреть газ.
Для этого делением первой пары уравнений
p A V p 2 V = ν R T 1 ν R T 2
получим выражение для давления нагретого газа:
p 2 = p A T 2 T 1
и подставим его в третье уравнение системы:
p A T 2 S T 1 = M g + p A S .
Преобразуем полученное выражение к виду
T 2 = T 1 ( M g + p A S ) p A S = T 1 ( M g p A S + 1 ) ,
а затем найдем разность
Δ T = T 2 − T 1 = M g T 1 p A S .
Δ T = 1,2 ⋅ 10 ⋅ 300 100 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 36 К = 36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см 2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
Решение . На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня M g → ;
- сила атмосферного давления F → A ;
- сила давления газа F → , действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a → :
F → + F → A + M g → = m a → ,
или в проекции на вертикальную ось —
где F — модуль силы давления газа под поршнем, F = pS ; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a = F − F A − M g M = ( p − p A ) S M − g .
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
и подставим в записанную формулу выражение для модуля ускорения:
v = 2 l ( ( p − p A ) S M − g ) .
v = 2 ⋅ 3,75 ( ( 450 − 100 ) ⋅ 10 3 ⋅ 50 ⋅ 10 − 4 75,0 − 10 ) ≈ 10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
В цилиндре под поршнем при постоянной температуре находится газ объем v газа при давлении
С1-1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-3. В цилиндре, закрытом подвижным поршнем, находится газ, который может просачиваться сквозь зазор вокруг поршня. В опыте по изотермическому сжатию газа его объем уменьшился вдвое, а давление газа упало в 3 раза. Во сколько раз изменилась внутренняя энергия газа в цилиндре? (Газ считать идеальным.)
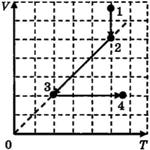
C1-5. Ha V T-диаграмме показано, как изменялись объём и температура некоторого постоянного количества разреженного газа при его переходе из начального состояния 1 в состояние 4. Как изменялось давление газа р на каждом из трёх участков 1—2, 2—3, 3—4: увеличивалось, уменьшалось или же оставалось неизменным? Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.
C1-6. В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают выдвигать из сосуда. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
С3-9. Нагреваемый при постоянном давлении идеальный одноатомный газ совершил работу 400 Дж. Какое количество теплоты было передано газу?
С3-11. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 8 раз, давление воздуха в сосуде увеличилось в 2 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)
С3-12. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 4 раза, давление воздуха в сосуде увеличилось тоже в 4 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)
С3-13. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔT. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на ΔT. Каким было изменение температуры ΔT в опытах? Масса азота m = 1 кг.
С3-14. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на 1 К. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на 1 К. Определите массу азота в опытах.
С3-15. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление p = 4 • 10 5 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газа поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3•10 3 H. Какое количество теплоты получил газ в этом процессе? Считать, что сосуд находится в вакууме.
С3-16. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 10 5 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты │Q│ = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня? Количество вещества газа постоянно.
С3-17. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа р1 = 4 · 10 5 Па. Расстояние от дна сосуда до поршня равно L. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтp = 3 · 10 3 Н. Найдите L. Считать, что сосуд находится в вакууме.
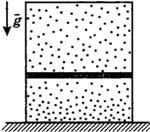
С3-18.Вертикальный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.
С3-19.В вертикальном теплоизолированном цилиндрическом сосуде под поршнем находится 0,5 моль гелия, нагретого до некоторой температуры. Поршень сначала удерживают, затем отпускают, и он начинает подниматься. Масса поршня 1 кг. Какую скорость приобретет поршень к моменту, когда поршень поднимется на 4 см, а гелий охладится на 20 К? Трением и теплообменом с поршнем пренебречь.
С3-20. Теплоизолированный сосуд объемом V = 2 м 3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль Не, а в другой — такое же количество моль А r . Температура гелия Т1 = 300 К, а температура аргона Т2 = 600 К. Определите парциальное давление аргона в сосуде после удаления перегородки.
Термодинамика С3-21. На рисунке изображено изменение состояния 1 моль идеального одноатомного газа. Начальная температура газа 27° С. Какое количество теплоты сообщено газу в этом процессе?
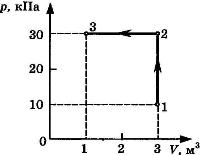
С3-23. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-24. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-25. На диаграмме (см. рисунок) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
В цилиндре под поршнем находится постоянная масса разреженного газа?
В цилиндре под поршнем находится постоянная масса разреженного газа.
Давление газа постоянно и равно 1, 5·105 Па.
На рисунке показаны результаты измерения объема газа с повышением температуры.
Погрешность измерения температуры ΔT = ± 10 К, объема ΔV = ± 0, 5 л.
Чему примерно равно число молей газа под поршнем?
5 * 10 ^ 5 V = 5 * 10 ^ - 3 R = 8.
31 T = 300 (температура и объем из графика)
v = p * V / (R * T) = 0.
3 моль (при других данных 0, 28 и 0, 31).
Зависимость объема газа от температуры при постоянном давлении?
Зависимость объема газа от температуры при постоянном давлении.
В вертикальном цилиндре под подвижным поршнем площадью 40 см ^ 2 находится 1 моль идеального газа при температуре 400К?
В вертикальном цилиндре под подвижным поршнем площадью 40 см ^ 2 находится 1 моль идеального газа при температуре 400К.
Определить в литрах объем газа, если масса поршня равна 40кг, а атмосферное давление 100кПа.
Трением поршня о стенки цилиндра пренебречь.
В цилиндре объемом 0, 7 м3 находится газ при температуре 280 К?
В цилиндре объемом 0, 7 м3 находится газ при температуре 280 К.
Определите работу газа при расширении в результате нагревания на 16 К, если давление постоянно и равно 100 кПа.
В сосуде с подвижным поршнем находится газ некоторой массы?
В сосуде с подвижным поршнем находится газ некоторой массы.
Газ сжали до вдвое меньше объема.
Как изменилось его давление если температура газа при сжатия не изменилась?
В цилиндре под поршнем изобарически охлаждается газ объемом 5л от температуры 333 К до температуры 273 К?
В цилиндре под поршнем изобарически охлаждается газ объемом 5л от температуры 333 К до температуры 273 К.
Каким станет объемом газа при температуре 273 К?
Как изменится давление массы газа, если температуру идеального газа при постоянном объеме уменьшить в 5 раз?
Как изменится давление массы газа, если температуру идеального газа при постоянном объеме уменьшить в 5 раз?
Если температуру идеального газа при постоянном объеме увеличить в 3 раза, то давление данной массы газа?
Если температуру идеального газа при постоянном объеме увеличить в 3 раза, то давление данной массы газа.
Идеальный одноатомный газ в количестве ν = 0, 09 моль находится в равновесии в вертикальном цилиндре под поршнем массой 5 кг?
Идеальный одноатомный газ в количестве ν = 0, 09 моль находится в равновесии в вертикальном цилиндре под поршнем массой 5 кг.
Трение между поршнем и стенками цилиндра отсутствует.
Внешнее атмосферное давление равно p = 100 кПа.
В результате нагревания газа поршень поднялся на высоту Δh = 4 см, а температура газа поднялась на ΔT = 16 К.
Чему равна площадь поршня?
Под поршнем вертикального цилиндра находится m = 2 кг гелия?
Под поршнем вертикального цилиндра находится m = 2 кг гелия.
Определите : а) малярные теплоемкости гелия при постоянном давлении постоянном объеме Сv б) изменение внутренней энергии газа в) механическую работу, совершенную газом при расширении.
В сосуде, закрытом поршнем, находится идеальный газ?
В сосуде, закрытом поршнем, находится идеальный газ.
График зависимости давления газа от температуры при изменениях его состояния представлен на рисунке.
Какому состоянию газа соответствует наименьшее значение объема?
V = 20 м / с m = 2 т = 2 * 10 ^ 3 кг g = 10 м / с ^ 2 h = ? Ek = m * V ^ 2 / 2 Ep = m * g * h Ek = Ep m * V ^ 2 / 2 = m * g * h Находим высоту, h = m * V ^ 2 / 2 * m * g Решаем, h = 2 * 10 ^ 3 * 400 / 2 * 2 * 10 ^ 3 * 10 = сокращаем 2 * 10 ^ 3, тогд..
530. дано : | решение h = p : p×g р = 22000Па| h = 22000÷1000×10 = 2 найти : h |2м.
По закону Менделеева - Клапейрона : p * V = m * R * T / M Но Vкв = √(3 * R * T / M) Vкв² = 3 * R * T / M R * T / M = Vкв² / 3 Тогда : p * V = m * Vкв² / 3 p = m * Vкв² / (3 * V) p = 0, 002 * 400² / (3 * 1 * 10⁻³)≈ 110 000 Па = 1, 1 * 10⁵ Па.
P = qgv F = pS F1 / F2 Подставишь.
R = ρl / s ; l = s * R / ρ = 0, 1 * 180 / 0, 4 = 45 метров.
1. проводниками 2. Потребители 3. Подсоединять 4. Одинакова 5. Заряды 6. Параллельном 7. 8. заряда 9. Наибольшая 10. 11. електроны.
Ну там трется а там скользит , трение создает тепло а скольжение это секундное действие.
Ответ смотри на фотографии.
40000 * 20 = х (20 + m) * 10000 = x 800000 = 200000 + 10000m m = 60.
M = 500гр в системе СИ 0. 5кг V = 36км / ч S = 36км в системе СИ 36 000м t = 1ч в системе СИ 3600с N - ? Решение Fт = gm = 10Н / кг * 0. 5кг = 5Н A = Fs = 5Н * 36000м = 180 000Дж N = A / t = 180 000 Дж / 3600с = 50Вт.
§ 3.12. Примеры решения задач
-
Если изменяются все три параметра, то следует воспользоваться уравнением состояния в форме (3.9.9) или (3.9.5).
Как измерить медицинским термометром температуру тела человека, если температура окружающего воздуха +42 °С?
Решение. Можно предварительно охладить термометр в холодильнике. Если холодильника нет, то нужно подержать термометр 5—8 мин под мышкой, извлечь его и сразу же стряхнуть. Термометр покажет температуру тела, так как ртуть в термометре сожмется при контакте с телом до объема, соответствующего температуре тела.
Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно р. Определите давление р1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
Решение. При горизонтальном положении цилиндра объем каждой его части обозначим через V (эти объемы равны). При вертикальном положении цилиндра объем верхней части станет равным V + ΔV, а нижней V - ΔV. Давление в нижней части цилиндра станет равным . Согласно закону Бойля— Мариотта

Исключив из этих равенств , получим квадратное уравнение для p1:


Второй корень квадратного уравнения отрицателен и потому лишен физического смысла.
Поршневой насос при каждом качании захватывает воздух объемом V0. При откачке этим насосом воздуха из сосуда объемом V насос совершил п качаний. Затем другой насос с тем же рабочим объемом V0 начал нагнетать воздух из атмосферы в тот же сосуд, совершив также п качаний. Какое давление установится в сосуде? Температуру воздуха во время работы насоса считать постоянной.
Решение. Согласно закону Бойля—Мариотта при откачке воздуха из сосуда после первого качания давление в сосуде станет равным , где p0— атмосферное давление.
После второго качания будет выполняться равенство p1V = p2(V + V0) и, следовательно, и т.д. После n качаний в сосуде установится давление
При нагнетании воздуха в сосуд после n качаний давление станет равным

При любом n р > р0, так как во время нагнетания воздуха при каждом качании насос захватывает воздух, имеющий атмосферное давление р0, а при откачке при каждом качании удаляется воздух при давлении, меньшем р0.
В запаянной с обоих концов цилиндрической трубке находится воздух при нормальных условиях. Трубка разделена подвижным поршнем на две части, объемы которых V1 и V2 относятся как 1 : 2. До какой температуры t1 следует нагреть воздух в меньшей части трубки и до какой t2 охладить в большей, чтобы поршень делил трубку на две равные части, если нагревание и охлаждение в обеих частях трубки производятся при условии = const?
Решение. Условие = const означает, что процессы нагревания и охлаждения происходят изобарно. При отношении начальных объемов эти объемы составляют и , где V0 — объем всей трубки. Конечные объемы обеих частей одинаковы и равны .
Согласно закону Гей-Люссака для воздуха в меньшей части трубки выполняется соотношение
а для воздуха в большей части
где Т0 = 273 К — температура, соответствующая начальным условиям. Отсюда

В цилиндре под поршнем находится воздух при давлении p1 = 2 • 10 5 Па и температуре t1 = 27 °С. Определите массу m груза, который нужно положить на поршень после нагревания воздуха до температуры t2 = 50 °С, чтобы объем воздуха в цилиндре стал равен первоначальному. Площадь поршня S = 30 см 2 .
Решение. Так как в процессе нагревания объем воздуха в цилиндре не изменяется, то согласно закону Шарля имеем

Подставляя в (3.12.1) выражение для р2, получим

Найдите среднюю (эффективную) молярную массу сухого атмосферного воздуха, предполагая известный процентный состав воздуха по массе: азот — n1 = 75,52%, кислород — n2 = 23,15%, аргон — n3 = 1,28% и углекислый газ — n4 = 0,05%.
Решение. Для каждого газа можно записать уравнение состояния:

Здесь M1, M2, M3 и M4 — молярные массы соответственно азота, кислорода, аргона и углекислого газа.
Складывая правые и левые части этих уравнений, получим

Для смеси газов выполняется соотношение
где m = m1 + m2 + m3 + m4 — масса воздуха с объемом V, а М — искомая эффективная молярная масса. Согласно закону Дальтона
Сравнивая уравнения состояния (3.12.2) и (3.12.3), получим

Разделив числитель и знаменатель на m и умножив на 100%, получим выражение для М через процентный состав воздуха по массе

Закрытый с обоих концов цилиндр наполнен газом при давлении p = 100 кПа и температуре t = 30 °С и разделен подвижным теплонепроницаемым поршнем на две равные части длиной L по 50 см. На какую величину ΔT нужно повысить температуру газа в одной половине цилиндра, чтобы поршень сместился на расстояние l = 20 см, если во второй половине цилиндра температура не изменяется? Определите давление газа после смещения поршня.
Решение. Для газа в части цилиндра с постоянной температурой применим закон Бойля—Мариотта:

где S — площадь основания цилиндра. Для нагреваемой части цилиндра запишем уравнение Клапейрона:

В уравнениях (3.12.4) и (3.12.5) р1 — давление газа после смещения поршня, одинаковое в обеих частях цилиндра вследствие равновесия поршня, а Т + ΔT в уравнении (3.12.5) — температура газа в нагретой части цилиндра.
Разделив почленно уравнение (3.12.4) на уравнение (3.12.5), получим
Из уравнения (3.12.4) находим p1:
Сосуд объемом V = 100 л разделен пополам полупроницаемой перегородкой. В начальный момент времени в одной половине сосуда находился водород, масса которого m1 = 2 г, а во второй — 1 моль азота. Определите давления, установившиеся по обе стороны перегородки, если она может пропускать только водород. Температура в обеих половинах одинакова и постоянна: t = 127 °С.
Решение. Так как водород свободно проходит через перегородку, то он распространяется по всему сосуду. Запишем уравнение Менделеева—Клапейрона для водорода после установления состояния равновесия:
где М1 = 2 • 10 -3 кг/моль — молярная масса водорода.
В той части сосуда, в которой вначале был только водород, он и в дальнейшем останется в чистом виде, так что давление в этой части сосуда станет равным

Для азота уравнение Менделеева—Клапейрона имеет вид
где р2 — давление азота.
Так как в этой половине находятся водород и азот, то полное давление р согласно закону Дальтона складывается из парциальных давлений р1 и р2, т. е.

Гелий массой 20 г, заключенный в теплоизолированном цилиндре под поршнем, медленно переводится из состояния 1 с объемом V1 = 32 л и давлением р1 = 4,1 атм в состояние 2 с объемом V2 = 9 л и давлением р2 = 15,5 атм. Какой наибольшей температуры достигнет газ при этом процессе, если на графике зависимости давления газа от объема процесс изображается прямой линией (рис. 3.18)?

Решение. Как следует из рисунка 3.18, давление и объем газа связаны линейной зависимостью: р = aV + b, где а и b — постоянные коэффициенты. Из условий задачи получаем систему уравнений

Решив эту систему относительно а и b, найдем

Подставив в уравнение Менделеева—Клапейрона вместо р выражение aV + b, получим

График зависимости Т от V представляет собой параболу (рис. 3.19).

Кривая достигает максимума при Vmax = = 20 л, когда корни квадратного уравнения (3.12.6) совпадают. При этом


На рисунке 3.20 изображен график изменения состояния идеального газа в координатах р, V. Начертите графики этого процесса в координатах V, Т и р, Т.

Решение. Из рисунка 3.20 следует, что давление газа р и его объем V находятся в прямой пропорциональной зависимости
где k — постоянный коэффициент. Подставив значение давления (3.12.7) в уравнение Менделеева— Клапейрона, получим

Уравнение (3.12.8) — это уравнение параболы, ось симметрии которой совпадает с осью Т. Следовательно, в координатах V, Т искомый график имеет вид, показанный на рисунке 3.21, а. Аналогично получим график этого процесса в координатах p, T (рис. 3.21, б).

- Вы надули щеки. При этом и давление, и объем воздуха во рту увеличиваются. Как это согласуется с законом Бойля— Мариотта?
- Чтобы измерить температуру человеческого тела, приходится держать термометр под мышкой в течение 5—8 мин. В то же время стряхнуть его можно практически сразу после измерения температуры. Почему?
- Узкая вертикальная трубка длиной L, закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути длиной h. Плотность ртути равна ρ. Трубка расположена открытым концом вверх. Какова была длина l столбика воздуха в трубке, если при перевертывании трубки открытым концом вниз из трубки вылилась половина ртути? Атмосферное давление равно р0.
- В ртутный барометр попал пузырек воздуха, вследствие чего барометр показывает давление меньше истинного. При давлении р1 = 768 мм рт. ст. уровень ртути расположен на высоте h1 = 748 мм, причем длина пустой части трубки l = 80 мм. Каково атмосферное давление р2, если ртуть стоит на высоте h2 = 734 мм? Плотность ртути ρ = 1,36 • 10 4 кг/м 3 .
- Площадь сечения цилиндра автомобильного насоса S = 10 см 2 . Определите длину l цилиндра, если известно, что для накачки шины объемом V = 0,02 м 3 от давления р0 = 1 • 10 5 Па до давления р = 3 • 10 5 Па требуется совершить n = 100 качаний. Утечкой и нагреванием воздуха пренебречь.
- В цилиндре под поршнем находится воздух. Поршень имеет форму, показанную на рисунке 3.22. Масса поршня m = 6 кг, площадь сечения цилиндра S = 20 см 2 . Атмосферное давление р0 = 10 5 Па. Найдите массу m1 груза, который надо положить на поршень, чтобы объем V1 воздуха в цилиндре уменьшился в 2 раза. Трение не учитывать. Температура постоянна.
Задание 12. МКТ, термодинамика. Установление соответствия . ЕГЭ 2022 по физике

С некоторой массой идеального газа был проведён циклический процесс, изображённый на рисунке. Укажите, как менялся объём газа при переходе из 1 → 2 и 4 → 1. Для каждого случая определите соответствующий характер изменения:
| Процессы | Характер изменения |
| A) Процесс 1 → 2 Б) Процесс 4 → 1 | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждого процесса. Цифры в ответе могут повторяться.
Решение
В процессе 1-2 объем газа не менялся, т.к. переход 1-2 - это изохора, покольку его продолжение идет через начало координат. Переход 4-1 - изобара, т.к. $p_1=p_4$, тогда $
Задача 10
В сосуде объёмом V при давлении p и температуре T находится идеальный газ массой m и молярной массой M . Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.
| Физические явления | Формулы |
| А) давление газа Б) температура газа | 1) $ 2) $ 3) $ 4) $ |
Решение
Из формул и формулировок МКТ очевидно, что $P=
Задача 11
По мере понижения температуры воды от +40◦С до −20◦С она находилась сначала в жидком состоянии, затем происходил процесс её отвердевания и дальнейшее охлаждение твёрдой фазы воды–льда. Изменялась ли внутренняя энергия воды во время этих процессов и если изменялась, то как? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Отвердевание воды Б) Охлаждение льда | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
1) Отвердевание воды и охлаждение льда два процесса, подчиняющихся первому началу термодинамики, согласно которому внутренняя энергия изменяется при совершении работы или передачи тепла. Следовательно, внутренняя энергия воды уменьшилась в ходе всех двух процессов.
Задача 12
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит шарик. Из сосуда выпускается половина газа при неизменной температуре. Как изменились в результате этого объём газа и действующая на шарик архимедова сила? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Объём газа Б) Архимедова сила | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если у сосуда выпустить половину газа, то атмосферное давление уравновесит давление поршнем и поршень передвинется вниз, вследствие чего, объем газа уменьшится. Архимедова же сила, действующая на шарик, не изменится, поскольку плотность газа под поршнем останется неизменной: $F_<арх>=p_г·g·V_ш$, где $g=9.8м/с^2$ - ускорение свободного падения, $V_ш$ - объем шарика, $p_г$ - плотность газа под поршнем.
Задача 13
Температуру нагревателя тепловой машины уменьшили, оставив температуру холодильника прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и количество теплоты, отданное газом за цикл холодильнику? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) КПД тепловой машины Б) Количество теплоты, отданное газом за цикл холодильнику | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если понизить температуру нагревателя при неизменной температуре холодильника, то КПД идеальной тепловой машины уменьшается в соответствие с уравнением: $η=(1-
Задача 14
Если налить воду в открытый сосуд, то она начнёт испаряться. Как будут меняться при этом её температура и внутренняя энергия? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
При испарении, жидкость покидают наиболее быстрые молекулы, поэтому средняя скорость остальных молекул жидкости становится меньше. Следовательно, и средняя кинетическая энергия остающихся в жидкости молекул уменьшается. Это означает, что температура жидкости и внутренняя энергия испаряющейся жидкости уменьшается.
Задача 15
Ученик наблюдает за процессом кипения воды, нагреваемой в кастрюле на электроплите. Как в процессе кипения меняется температура и внутренняя энергия системы «вода–пар»? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
При кипении, температура системы "вода-пар" остается постоянной, а внутренняя энергия данной системы увеличивается, т.к. происходит поглощение тепловой энергии.
Задача 16
В вертикальном цилиндрическом сосуде под поршнем, способным перемещаться без трения, находится воздух.Как изменятся температура газа и его объём, если поршень быстро сместить вниз? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Температура Б) Объём | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если поршень быстро сместить вниз, то объем газа уменьшится, давление - увеличится, а так как давление связано с температурой соотношением: $p=nkT$, то и температура тоже увеличится.
Задача 17
В вертикальном цилиндрическом сосуде под поршнем, способным перемещаться без трения, находится воздух. Как изменятся давление газа и его внутренняя энергия, если поршень быстро сместить вверх? Для каждой величины определите соответствующий характер изменения:
| Физические величины | Характер изменения |
| A) Давление Б) Внутренняя энергия | 1) увеличится 2) уменьшится 3) не изменится |
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
Если поршень сместить вверх, то обмен с окружающейс средой произойти не успеет - процесс будет адиабатным. Тогда из 1 закона термодинамики $Q=0=A+∆U$, тогда $∆U=-A$. Газ расширяется, значит $A>0$, следовательно, и $∆U T_1$, то при повышении температуры воздуха скорость его молекул увеличится, это приведет к увеличению ударов молекул о стенки сосуда и поршня, а следовательно, к увеличению давления, что приведет к тому, что поршень сместится, увеличив объем газа, плотность же газа, уменьшится, поскольку $p=
Читайте также: