при повышении температуры газа в закрытом цилиндре на 30 процентов
Изменение состояния идеального газа
827. Резиновую лодку надули утром, когда температура воздуха была 7°С. На сколько процентов увеличилось давление воздуха в лодке, если днем он прогрелся под лучами солнца до 21°С? Объем лодки не изменился. (5)
828. При нагревании газа при постоянном объеме на 1 К давление увеличилось на 0,2%. При какой начальной температуре (в °С) находился газ? (227)
829. Воздух в открытом сосуде медленно нагрели до 400 К, затем сосуд герметично закрыли и охладили до 280 К. На сколько процентов при этом изменилось давление в сосуде? (30)
830. В цилиндре под поршнем находится газ. Чтобы поршень оставался в неизменном положении при увеличении абсолютной температуры газа в 2 раза, на него следует положить груз массой 10 кг. Площадь поршня 10 см2. Найдите первоначальное давление (в кПа) газа. g = 10 м/с2.(100)
831. Газ находится в вертикальном цилиндре под поршнем массой 5 кг. Какой массы груз надо положить на поршень, чтобы он остался в прежнем положении, когда абсолютная температура газа будет увеличена вдвое? Атмосферное давление 100 кПа, площадь поршня 0,001 м2. g = 10 м/с2. (15)
832. Давление воздуха внутри плотно закупоренной бутылки при температуре 7°С равно 150 кПа. До какой температуры (по шкале Цельсия) надо нагреть бутылку, чтобы из нее вылетела пробка, если известно, что для вытаскивания пробки до нагревания бутылки требовалась минимальная сила 45 Н? Площадь поперечного сечения пробки 4 см2. (217)
833. Сначала газ нагревают изохорно от 400 К до 600 К, а затем нагревают изобарно до температуры Т. После этого газ приводят в исходное состояние в процессе, при котором давление уменьшается прямо пропорционально объему газа. Найдите температуру Т (в кельвинах). (900)
в) Изотермический процесс
835. Под каким давлением (в кПа) надо наполнить воздухом баллон емкостью 10 л, чтобы при соединении его с баллоном емкостью 30 л, содержащим воздух при давлении 100 кПа, установилось общее давление 200 кПа? Температура постоянна. (500)
836. Два сосуда соединены тонкой трубкой с краном. В первом сосуде объемом 15 дм3находится газ под давлением 2 атм, во втором — такой же газ под давлением 10 атм. Если открыть кран, то в обоих сосудах устанавливается давление 4 атм. Найдите объем (в дм3) второго сосуда. Температура постоянна. (5)
837. До какого давления (в кПа) накачан футбольный мяч емкостью 3 л, если при этом было сделано 40 качаний поршневого насоса? За каждое качание насос захватывает из атмосферы 150 см3воздуха. Атмосферное давление 100 кПа. Содержанием воздуха в мяче до накачки пренебречь. Температура постоянна. (200)
838. Давление воздуха в сосуде было равно 105 Па. После трех ходов поршня откачивающего насоса давление воздуха упало до 800 Па. Определите, во сколько раз объем цилиндра насоса больше объема сосуда. Температура постоянна. (4)
839. Объем цилиндра поршневого насоса равен объему откачиваемого сосуда. Чему будет равно давление в сосуде после 5 ходов поршня насоса? Начальное давление в сосуде равнялось 105 Па. Температура постоянна. (3125)
840. Газ находится в цилиндре под поршнем и занимает объем 240 см3при давлении 105 Па. Какую силу надо приложить перпендикулярно к плоскости поршня, чтобы сдвинуть его на 2 см, уменьшив объем газа? Площадь поршня 24 см2. (60)
841. Газ находится в высоком цилиндре под тяжелым поршнем, который может перемещаться без трения. Площадь поршня 30 см2. Когда цилиндр перевернули открытым концом вниз, объем газа увеличился в 3 раза. Чему равна масса поршня? Атмосферное давление 100 кПа, g = 10 м/с2. (15)
842. Воздух находится в вертикальном цилиндре под поршнем массой 20,2 кг и сечением 20 см2. После того, как цилиндр стали перемещать вертикально вверх с ускорением 5 м/с2, высота столба воздуха в цилиндре уменьшилась на 20%. Считая температуру постоянной, найдите атмосферное давление (в кПа). g = 10 м/с2. (101)
843. В сосуде, закрытом пробкой, находится воздух под давлением 0,5×105 Па. Какой объем воды (в л) войдет в сосуд, если его опустить в воду открытым концом вниз на глубину 10 м и открыть пробку? Объем сосуда 4 л, атмосферное давление 105 Па, g = 10 м/с2. Температура в толще воды и у ее поверхности одинакова. (3)
844. На какой глубине объем пузырька воздуха, поднимающегося со дна водоема, в 3 раза меньше, чем на поверхности? Атмосферное давление 100 кПа, g = 10 м/с2. Температура в толще воды и у ее поверхности одинакова. (20)
845. Пузырек воздуха поднимается со дна водоема глубиной 35 м. Во сколько раз объем пузырька на глубине 5 м больше, чем у дна водоема? Атмосферное давление 100 кПа, g = 10 м/с2. Температура в толще воды и у ее поверхности одинакова. (3)
846. На какой глубине радиус пузырька воздуха, поднимающегося со дна водоема, в 2 раза меньше, чем на поверхности? Атмосферное давление 100 кПа, g = 10 м/с2. Температура в толще воды и у ее поверхности одинакова. (70)
847. В горизонтальной пробирке находится 240 см3воздуха, отделенных от атмосферы столбиком ртути длиной 150 мм. Если пробирку повернуть открытым концом вверх, то объем воздуха станет 200 см3. Найдите атмосферное давление (в кПа). Плотность ртути 13600 кг/м3, g = 10 м/с2. (102)
848. Открытая с обеих сторон вертикальная цилиндрическая трубка длиной 1 м наполовину погружена в ртуть. Затем верхнее отверстие трубки плотно закрывают и вынимают трубку из ртути. В трубке остается столбик ртути длиной 25 см. Определите по этим данным атмосферное давление (в кПа). Плотность ртути 13600 кг/м3, g = 10 м/с2. (102)
849. Трубку длиной 42 см, запаянную с одного конца, погружают открытым концом в ртуть. Какой будет длина (в см) столбика воздуха в трубке в тот момент, когда верхний конец трубки сравняется с уровнем ртути? Атмосферное давление 750 мм рт.ст. (30)
850. В трубке, закрытой с одного конца, столбик воздуха заперт столбиком ртути длиной 19 см. Если трубку повернуть открытым концом вниз, длина столбика воздуха будет 10 см, а если открытым концом вверх, то 6 см. Найдите атмосферное давление (в мм рт. ст.). (760)
851. В длинной горизонтальной трубке, открытой с одного конца, столбик воздуха длиной 16 см заперт столбиком ртути длиной 20 см. Трубку приводят во вращение вокруг вертикальной оси, проходящей через ее закрытый конец. При какой угловой скорости столбик ртути сместится на 4 см? Атмосферное давление 750 мм рт.ст., g = 10 м/с2. (5)
852. Тонкостенный стакан массой 50 г ставят вверх дном на поверхность воды и медленно погружают так, что он все время остается в вертикальном положении. Высота стакана 10 см, площадь дна 20 см2. На какую минимальную глубину надо опустить стакан, чтобы он утонул? Атмосферное давление 100 кПа, g = 10 м/с2. Глубина отсчитывается от поверхности воды до уровня воды в стакане на искомой глубине. Температура у поверхности и на глубине одинакова. Массой воздуха в стакане пренебречь. (30)
Объединенный газовый закон
853. При уменьшении объема газа в 2 раза давление изменилось на 120 кПа, а абсолютная температура возросла на 10%. Каково было первоначальное давление (в кПа) газа? (100)
854. На сколько процентов надо уменьшить абсолютную температуру газа при увеличении его объема в 7 раз, чтобы давление упало в 10 раз? (30)
855. Два сосуда соединены тонкой трубкой с краном. Один из сосудов объемом 3 л заполнен газом при давлении 10 кПа, в другом сосуде объемом 6 л давление пренебрежимо мало. Температура газа в первом сосуде 27°С. Какое давление (в кПа) установится в сосудах, если открыть кран, а температуру газа повысить до 177°С? (5)
856. При каждом ходе поршневой насос захватывает 10 дм3воздуха из атмосферы при нормальных условиях (Т0 = 273 К) и нагнетает его в резервуар объемом 10 м3. Температура в резервуаре постоянна и равна 364 К. Сколько ходов должен сделать поршень насоса, чтобы повысить давление в резервуаре от нормального (pо= 1 атм) до 10 атм? (6750)
857. Воздух в цилиндре под поршнем сначала изотермически сжали, увеличив давление в 2 раза, а затем нагрели при постоянном давлении. В результате объем воздуха увеличился в 3 раза по сравнению с начальным. До какой температуры (в кельвинах) нагрели воздух, если его начальная температура была 300 К? (1800)
858. Газ, занимающий при температуре 127°С и давлении 200 кПа объем 3 л, изотермически сжимают, затем изобарно охлаждают до температуры 73°С, после чего изотермически изменяют объем до 1 л. Найдите конечное давление (в кПа) газа. (300)
859. Газ, находящийся в цилиндре под поршнем, нагрели при постоянном давлении так, что его объем увеличился в 1,5 раза. Затем поршень закрепили и нагрели газ так, что его давление возросло в 2 раза. Чему равно отношение конечной абсолютной температуры газа к его начальной абсолютной температуре? (3)
861. Теплоизолирующий поршень делит горизонтальный сосуд на две равные части, содержащие газ при температуре 7°С. Длина каждой части 30 см. Когда одну часть сосуда нагрели, поршень сместился на 2 см. На сколько градусов нагрели газ? Температура газа в другой части сосуда не изменилась. (40)
862. Теплоизолирующий поршень делит горизонтальный сосуд на две равные части, содержащие газ при температуре 5°С. Длина каждой части 144 мм. Одну часть сосуда нагрели на 18°С, а другую — на 2°С. На какое расстояние (в мм) сместится поршень? (4)
863. Баллон емкостью 40 л содержит сжатый воздух под давлением 18 МПа при 27°С. Какой объем (в л) воды можно вытеснить из цистерны подводной лодки воздухом этого баллона, если лодка находится на глубине 20 м, где температура 7°С? Атмосферное давление 0,1 МПа, g = 10 м/с2. (2200)
864. Во сколько раз уменьшится радиус тонкого резинового шара, заполненного воздухом, если его опустить в воду на глубину 65,2 м? Давление у поверхности воды 100 кПа. Температура воды у поверхности 27°С, на глубине 9°С. g = 10 м/с2. (2)
865. В сообщающихся сосудах одинакового сечения находится ртуть. Один из сосудов закрывают и увеличивают температуру воздуха в нем от 300 К до 400 К. Найдите образовавшуюся разность уровней (в см) ртути, если начальная высота столба воздуха в запертом сосуде была 10 см. Атмосферное давление 750 мм рт.ст. (5)
Тепловое расширение. Газовые законы
В два сосуда конической формы, расширяющихся кверху и книзу, и цилиндрический налита вода при температуре T = 100 °C. Как изменится давление на дно сосудов после охлаждения воды до комнатной температуры?
В сосуде конической формы, расширяющемся кверху, давление на дно увеличится. В сосуде конической формы, расширяющемся книзу, давление на дно уменьшится. В цилиндрическом сосуде давление на дно не изменится.
Две линейки — одна медная, другая железная — наложены одна на другую так, что они совпадают только одним концом. Определить длины линеек при t = 0 °C, зная, что разность их длин при любой температуре составляет Δl = 10 см. Коэффициент линейного расширения меди α1 = 17·10 -6 К -1 , железа — α2 = 12·10 -6 К -1 .
Длина медной линейки 24 см, длина железной — 34 см.
Часы, маятник которых состоит из груза малых размеров и легкой латунной нити, идут правильно при 0 °C. Найти коэффициент линейного расширения латуни, если при повышении температуры до t = +20 °C часы отстанут за сутки на 16 с.
На сколько часы будут уходить вперед за сутки при t0 = 0 °C. если они выверены при t = 20 °C, и материал, из которого сделан маятник, имеет коэффициент линейного расширения α = 0,000012 К -1 ?
При t0 = 0 °С часы спешат в сутки на τ = 20 с. При какой температуре часы будут идти точно? Коэффициент линейного расширения материала маятника α = 1,9·10 -5 К -1 .
Какую силу F надо приложить к стальному стержню сечением S = 1 см 2 , чтобы растянуть его на столько же, на сколько он удлиняется при нагревании на Δt = 1 °С? Коэффициент линейного расширения α = 12·10 -6 К -1 . Модуль Юнга E = 2,1·10 11 Н/м 2 .
Толщина биметаллической пластинки, составленной из одинаковых полосок стали и цинка, равна d = 0,1 см. Определить радиус кривизны r пластинки при повышении температуры на Δt = 11 °С. Коэффициент линейного расширения цинка α1= 25·10 -6 К -1 , а стали α2 = 12·10 -6 К -1 .
Концы стального стержня сечением S = 1 см 2 , находящегося при температуре t = 20 °С, прочно закреплены. С какой силой стержень будет действовать на опоры, если его нагреть до t1 = 200 °С? Модуль Юнга стали E = 2,0·10 11 Н/м 2 , коэффициент линейного расширения α =1,2·10 -5 К -1 ?
F = 39600 Н.
Каково давление газа p0 в электрической лампочке, объем которой V = 1 л, если при отламывании кончика последней под поверхностью воды на глубине h = 1 м в лампочку вошло m = 998,7 г воды? Атмосферное давление нормальное.
Стеклянный баллон объемом V = 1 л был наполнен испытуемым газом до давления p = 10 5 Па и взвешен. Его вес оказался равным Q = 0,9898 Н. Затем часть газа была удалена так, что давление в баллоне упало до р1 = 5·10 4 Па. Новый вес баллона оказался равным Q1 = 0,9800 Н. Какова плотность испытуемого газа при нормальном атмосферном давлении? Температура постоянна.
ρ = 2,1 кг/м 3 .
p1 = 751 мм рт. ст.
Открытую стеклянную трубку длиной l = 1 м наполовину погружают в ртуть. Затем трубку закрывают пальцем и вынимают. Какой длины столбик ртути останется в трубке? Атмосферное давление равно H = 750 мм рт. ст.
В запаянной с одного конца стеклянной трубке длиной l = 90 см находится столбик воздуха, запертый сверху столбиком ртути высотой h = 30 см; столбик ртути доходит до верхнего края трубки. Трубку осторожно переворачивают открытым концом вниз, причем часть ртути выливается. Какова высота столбика ртути, которая останется в трубке, если атмосферное давление H = 750 мм рт. ст.?
В сосуд со ртутью опускают открытую стеклянную трубку, оставляя над поверхностью конец длиной l = 60 см. Затем трубку закрывают и погружают еще на 30 см. Определить высоту столба воздуха в трубке. Атмосферное давление p0 = 760 мм рт. ст.
.
Посередине откачанной и запаянной с обоих концов горизонтальной трубки длиной L = 1 м находится столбик ртути длиной h = 20 см. Если трубку поставить вертикально, столбик ртути сместится на l = 10 см. До какого давления была откачана трубка? Плотность ртути ρ = 1,36·10 4 кг/м.
Расположенная горизонтально запаянная с обоих концов стеклянная трубка разделена столбиком ртути, на две равные части. Длина каждого столбика воздуха 20 см. Давление 750 мм рт. ст. Если трубку повернуть вертикально, ртутный столбик опускается на 2 см. Определить длину столбика ртути.
Цилиндрический сосуд делится на две части тонким подвижным поршнем. Каково будет равновесное положение поршня, когда в одну часть сосуда помещено некоторое количество кислорода, в другую — такое же по массе количество водорода, если длина сосуда l = 85 см?
В закрытом цилиндрическом сосуде с площадью основания S находится газ, разделенный поршнем массой M на два равных отсека. Масса газа под поршнем при этом в k раз больше массы газа над ним. Температуры газов одинаковы. Пренебрегая трением и массой газа по сравнению с массой поршня, найти давление газа в каждом отсеке.
; .
Имеются два мяча различных радиусов, давление воздуха в которых одинаково. Мячи прижимают друг к другу. Какой формы будет поверхность соприкосновения?
Выгнута в сторону мяча с большим радиусом.
Найти число n ходов поршня, которое надо сделать, чтобы поршневым воздушным насосом откачать воздух из сосуда емкостью V от давления p0 до давления p, если емкость насоса ΔV.
.
Упругость воздуха в сосуде равна 97 кПа. После трех ходов откачивающего поршневого насоса упругость воздуха упала до 28,7 кПа. Определить отношение объемов сосуда и цилиндра насоса.
Два баллона соединены трубкой с краном. В первом находится газ при давлении p = 10 5 Па, во втором — при p1 = 0,6·10 5 Па. Емкость первого баллона V1 = 1 л, второго — V2 = 3 л. Какое давление установится в баллонах (в мм рт. ст.), если открыть кран? Температура постоянная. Объемом трубки можно пренебречь.
Три баллона емкостями V1 = 3 л, V2 = 7 л и V3 = 5 л наполнены соответственно кислородом (p1 = 2·10 5 Па), азотом (p2 = 3·10 5 Па) и углекислым газом (p3 = 6·10 4 Па), при одной и той же температуре. Баллоны соединяют между собой, причем образуется смесь той же температуры. Каково давление смеси?
На гладком горизонтальном столе находится сосуд, разделенный перегородкой на две равные части. В одной части сосуда находится кислород, а в другой — азот. Давление азота вдвое больше давления кислорода. На сколько сдвинется сосуд, если перегородка станет проницаемой? Длина сосуда l = 20 см. Массой сосуда пренебречь. Процесс считать изотермическим.
В цилиндре, закрытом легко подвижным поршнем массой m и площадью S, находится газ. Объем газа равен V. Каким станет объем газа, если цилиндр передвигать вертикально с ускорением: а) +a; б) -a? Атмосферное давление равно p0, температура газа постоянна.
а) ; б) .
Начертить графики изотермического, изобарического и изохорического процессов в идеальном газе в координатах p, V; p, T; V, T. Объяснить, почему коэффициент объемного расширения идеальных газов равен термическому коэффициенту давления.
На рисунке изображены две изотермы одной и той же массы газа.

1. Чем отличаются состояния газов, если газы одинаковы?
2. Чем отличаются газы, если температуры газов одинаковы?
Как менялась температура идеального газа — увеличивалась или уменьшалась — при процессе, график которого в координатах p, V изображен на рисунке.

При нагревании газа получен график зависимости давления от абсолютной температуры в виде прямой, продолжение которой пересекает ось p в некоторой точке выше (ниже) начала координат. Определить, сжимался или расширялся газ во время нагревания.
На рисунке дан график изменения состояния идеального газа в координатах p, V.

Представить этот круговой процесс (цикл) в координатах p, T и V, T, обозначив соответствующие точки.
Сколько ртути войдет в стеклянный баллончик объемом 5 см 3 , нагретый до t1 = 400 °С, при его остывании до t2 = 16 °С, если плотность ртути при t = 16 °С равна ρ = 13,6 г/см 3 ?

При какой температуре находился газ, если при нагревании его на Δt = 22 °С при постоянном давлении объем удвоился? Для каких газов это возможно?
До какой температуры нужно нагреть воздух, взятый при t = 20 °С, чтобы его объем удвоился, если давление останется постоянным?
Определить, каким был бы коэффициент объемного расширения идеального газа, если бы за начальный объем его принимали объем не при t0 =0°С, а при t1 = 100 °С?
В цилиндре, площадь основания которого равна S = 100 см 2 , находится воздух при температуре t1 = 12 °С. Атмосферное давление p1 = 101 кПа. На высоте h1 = 60 см от основания цилиндра расположен поршень. На сколько опустится поршень, если на него поставить гирю массой m = 100 кг, а воздух в цилиндре при этом нагреть до t2 = 27 °С? Трение поршня о стенки цилиндра и вес самого поршня не учитывать.
Два одинаковых баллона, содержащие газ при t = 0 °С, соединены узкой горизонтальной трубкой диаметром d = 5 мм, посередине которой находится капелька ртути.

Капелька делит весь сосуд на два объема по V = 200 см 3 . На какое расстояние x переместится капелька, если один баллон нагреть на Δt = 2 °С, а другой на столько же охладить? Изменением объемов сосудов пренебречь.
Два одинаковых сосуда соединены трубкой, объемом которой можно пренебречь. Система наполнена газом и находится при абсолютной температуре T. Во сколько раз изменится давление в такой системе, если один из сосудов нагреть до абсолютной температуры T1, а другой поддерживать при прежней температуре T?
1. В горизонтально расположенном сосуде, разделенном легко подвижным поршнем, находятся с одной стороны от поршня m1 граммов кислорода, а с другой — m2 граммов водорода. Температуры газов одинаковы и равны T0. Каким будет отношение объемов, занимаемых газами, если температура водорода останется равной T0, а кислород нагреется до температуры T1?
2. Вертикально расположенный сосуд разделен на две равные части тяжелым теплонепроницаемым поршнем, который может скользить без трения. В верхней половине сосуда находится водород при температуре T и давлении p. В нижней части — кислород при температуре 2T. Сосуд перевернули. Чтобы поршень по-прежнему делил сосуд на две равные части, пришлось охладить кислород до температуры T/2. Температура водорода осталась прежней. Определить давление кислорода в первом и втором случаях.
На некоторой высоте давление воздуха p = 3·10 4 Па, а температура t = -43 0 С. Какова плотность воздуха на этой высоте?
Определить давление кислорода, масса которого m = 4 кг, заключенного в сосуд емкостью V = 2 м 3 , при температуре t = 29 °С.
Определить удельный объем азота при температуре 27 °С и давлении p = 4,9·10 4 Па.
Определить массу кислорода, заключенного в баллоне емкостью V = 10 л, если при температуре t = 13 °С манометр на баллоне показывает давление p = 9·10 6 Па.
Какова разница в массе воздуха, заполняющего помещение объемом V = 50 м 3 , зимой и летом, если летом температура помещения достигает t1 = 40 °С, а зимой падает до t2 = 0 °С? Давление нормальное.
Сколько молекул воздуха выходит из комнаты объемом V0 = 120 м 3 при повышении температуры от t1 = 15 °С до t2 = 25 °С? Атмосферное давление p0 = 10 5 Па.
Компрессор захватывает при каждом качании V0 = 4 л воздуха при атмосферном давлении p = 10 5 Па и температуре t0 = -3 °С и нагнетает его в резервуар емкостью V = 1,5 м 3 , причем температура воздуха в резервуаре держится около t1 = 45 °С. Сколько качаний должен сделать компрессор, чтобы давление в резервуаре увеличилось на Δp = 1,96·10 5 Па?
На весах установлены два одинаковых сосуда. Один заполнен сухим воздухом, другой — влажным (насыщенный водяными парами) при одинаковых давлениях и температурах. Какой из сосудов тяжелее?
По газопроводу течет углекислый газ при давлении p = 5·10 5 Па и температуре t = 17 °С. Какова скорость движения газа в трубе, если за τ = 5 мин через площадь поперечного сечения трубы S = 6 см 2 протекает m = 2,5 кг углекислого газа?
Из баллона со сжатым водородом емкостью V = 10 л вследствие неисправности вентиля утекает газ. При температуре t1 = 7 °С манометр показывал p = 5·10 6 Па. Через некоторое время при температуре t2 = 17 °С манометр показал такое же давление. Сколько утекло газа?
Какая часть газа осталась в баллоне, давление в котором было равно p = 1,2·10 7 Па, а температура t = 27 °С, если давление упало до p1 = 10 5 Па? Баллон при этом охладился до t1 = -23 °С.
До какой температуры нужно нагреть запаянный шар, содержащий m = 17,5 г воды, чтобы шар разорвался, если известно, что стенки шара выдерживают давление 10 7 Па, а объем шара V = 1 л?
В цилиндре объемом V, заполненном газом, имеется предохранительный клапан в виде маленького цилиндрика с поршнем. Поршень упирается в дно цилиндра через пружину жесткости k.

При температуре T1 поршень находится на расстоянии l от отверстия, через которое газ выпускается в атмосферу. До какой температуры T2 должен нагреться газ в цилиндре, для того чтобы клапан выпустил часть газа в атмосферу? Площадь поршня S, масса газа в цилиндре m, его молярная масса µ. Объем цилиндрика клапана пренебрежимо мал по сравнению с объемом цилиндра.
В баллоне емкостью V = 110 л помещено m1 = 0,8 кг водорода и m2 = 1,6 кг кислорода. Определить давление смеси на стенки сосуда. Температура окружающей среды t = 27 °С.
В сосуде объемом 1 л заключено m = 0,28 г азота. Азот нагрет до температуры T = 1500 °С. При этой температуре α = 30% молекул азота диссоциировано на атомы. Определить давление в сосуде.
В сосуде находится смесь азота и водорода. При температуре T, когда азот полностью диссоциирован на атомы, давление равно p (диссоциацией водорода можно пренебречь). При температуре 2T, когда оба газа полностью диссоциированы, давление в сосуде 3p. Каково отношение масс азота и водорода в смеси?
Оболочка аэростата объемом V = 1600 м 3 , находящегося на поверхности Земли, наполнена водородом на n = 7/8 при давлении p = 101 кПа и температуре t = 15 °С. Аэростат поднялся на некоторую высоту, где давление p1 = 79,3 кПа и температура t1 = 2 °С. Сколько водорода потерял аэростат при своем подъеме в результате расширения газа?
Доказать, что в атмосфере с постоянной температурой независимо от закона изменения давления с высотой подъемная сила воздушного шара с эластичной оболочкой постоянна. Газ из воздушного шара не вытекает. Пренебречь давлением, обусловленным кривизной оболочки.
в закрытом сосуде находится газ по давлением 200 кПа. Каким станет давление газа, если температуру повысить на 30% ?
Запишем уравнение Менделеева - Клапейрона для двух случаев (Объем одинаков).
Поделим одно на другое, получим:
Извиняюсь за задержку, времени напечатать не было:)
200кПа раздели на 100% и умножь на 30 % получится 200 кПа + 60 Кпа равно 260 кПа
Другие вопросы из категории
1-увеличилась путем совершения работы
2-уменьшилась благодаря совершению работы
3- увеличилась вследствие теплопередачи4-неизменилась
2)Мальчик,стоя на одной ноге,оказывает давление 40 кПа.Как изменится давление,если он будет стоять на обеих ногах?
3)Задача.В сосуд,имеющий форму куба,налили 8м(в кубе) воды.Найдите её давление на дно сосуда.Плотность воды 1000кг/м(в кубе)?
Помогите пожалуйста)
давлении 515 кПа.Какая работа совершается газом?
Какое количество теплоты ( в кДж) нужно сообщить 1 кг воды, взятой при 0 C, чтобы нагреть её до 100 C и полностью испарить?
В вертикально расположенном цилиндре с площадью основания 1,2 дм2 находится воздух , закрытый подвижным поршнем массой 2,5 кг. Первоначальный обьём воздуха 5 л. При изобарном нагревании на 850К была совершена работа 1,5 кДж . Определить первоначальную температуру воздуха. Наружное давление равно 100 кПа.
2) Из чего можно заключить,что давление газа по всему направлению одинаково?
3) Какое свойство жидкостей и газов используют в гидравлических и пневматических машинах?
2)С одинаковой высоты на кафельный пол падают три шарика равной массы:один шарик-медный,другой -стальной,третий-железный.Какой из них нагреется до более высокой температуры?
3)При изометрическом сжатии газ передал окружающим телам теплоту 800 Дж.Какую работу совершил газ?
4)При изохорном охлаждении внутренняя энергия газа уменьшилась на 250 Дж.Какую работу совершил при этом газ?
5)При адиабальном процессе газом была совершена работа 350 Дж.Как и насколько изменилась его внутренняя энергия?
6)Газ при изотермическом процессе совершает работу.За счёт чего это происходит?
При повышении температуры газа в закрытом цилиндре на 30 процентов
С1-1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-3. В цилиндре, закрытом подвижным поршнем, находится газ, который может просачиваться сквозь зазор вокруг поршня. В опыте по изотермическому сжатию газа его объем уменьшился вдвое, а давление газа упало в 3 раза. Во сколько раз изменилась внутренняя энергия газа в цилиндре? (Газ считать идеальным.)
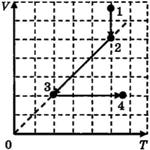
C1-5. Ha V T-диаграмме показано, как изменялись объём и температура некоторого постоянного количества разреженного газа при его переходе из начального состояния 1 в состояние 4. Как изменялось давление газа р на каждом из трёх участков 1—2, 2—3, 3—4: увеличивалось, уменьшалось или же оставалось неизменным? Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.
C1-6. В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают выдвигать из сосуда. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
С3-9. Нагреваемый при постоянном давлении идеальный одноатомный газ совершил работу 400 Дж. Какое количество теплоты было передано газу?
С3-11. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 8 раз, давление воздуха в сосуде увеличилось в 2 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)
С3-12. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 4 раза, давление воздуха в сосуде увеличилось тоже в 4 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.)
С3-13. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔT. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на ΔT. Каким было изменение температуры ΔT в опытах? Масса азота m = 1 кг.
С3-14. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на 1 К. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на 1 К. Определите массу азота в опытах.
С3-15. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление p = 4 • 10 5 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газа поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3•10 3 H. Какое количество теплоты получил газ в этом процессе? Считать, что сосуд находится в вакууме.
С3-16. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 10 5 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты │Q│ = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня? Количество вещества газа постоянно.
С3-17. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа р1 = 4 · 10 5 Па. Расстояние от дна сосуда до поршня равно L. Площадь поперечного сечения поршня S = 25 см 2 . В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтp = 3 · 10 3 Н. Найдите L. Считать, что сосуд находится в вакууме.
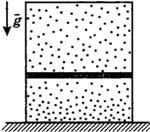
С3-18.Вертикальный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.
С3-19.В вертикальном теплоизолированном цилиндрическом сосуде под поршнем находится 0,5 моль гелия, нагретого до некоторой температуры. Поршень сначала удерживают, затем отпускают, и он начинает подниматься. Масса поршня 1 кг. Какую скорость приобретет поршень к моменту, когда поршень поднимется на 4 см, а гелий охладится на 20 К? Трением и теплообменом с поршнем пренебречь.
С3-20. Теплоизолированный сосуд объемом V = 2 м 3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль Не, а в другой — такое же количество моль А r . Температура гелия Т1 = 300 К, а температура аргона Т2 = 600 К. Определите парциальное давление аргона в сосуде после удаления перегородки.
Термодинамика С3-21. На рисунке изображено изменение состояния 1 моль идеального одноатомного газа. Начальная температура газа 27° С. Какое количество теплоты сообщено газу в этом процессе?
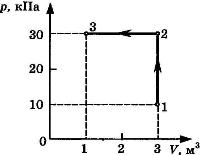
С3-23. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-24. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-25. На диаграмме (см. рисунок) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
Задание 30. Молекулярная физика (расчетная задача). ЕГЭ 2022 по физике
Найдите плотность водорода при температуре 15◦С и давлении 730 мм рт. ст.
Решение
Плотность по определению равна: $ρ=
Из уравнения Менделеева-Клайперона имеем: $pV=
Задача 2
Автомобиль потребляет 10 л бензина на 100 км пути при скорости 108 км/ч. Определите КПД двигателя, если его мощность равна 50 кВт. Удельная теплота сгорания бензина 4,6 · 10 7 Дж/кг, плотность бензина ρ = 700 кг/м 3 .
Решение
Задача 3
Кусок свинца массой 2 кг нагрели, сообщив ему 110 кДж теплоты. Свинец расплавился на 50% своей массы. Какова была начальная температура свинца? Температура плавления свинца 600 К, удельная теплоёмкость свинца 130 Дж/(кг·К)
Решение
Общее количество теплоты, которое сообщили свинцу массой $m$ равно: $Q=Q_1+Q_2$(1), где $Q_1=cm(T_2-T_1)$(2) - количество теплоты, которое сообщили свинцу до температуры плавления $T_2$. $Q_2=m_2·λ=0.5m·λ$(3), где $λ$ - удельная теплота плавления свинца, $c$ - удельная теплоемкость свинца. Подставим (2) и (3) в (1): $Q=cmT_2-cmT_1+0.5mλ$, откуда найдем температуру $T_1$: $cmT_1=cmT_2+0.5mλ-Q; T_1=
Задача 4
Газ в сосуде находится под давлением 300 кПа при температуре 227◦C. Определите давление газа после того, как половина массы газа выпущена из сосуда, а температура понижена на 80◦C.
Решение
Найдем абсолютную температуру $T_1$: $T_1=273+t_1=273+227=500K$, тогда $T_2=T_1-∆T=500-80=420K$,
Из уравнения Менделеева-Клайперона имеем:
$p_1·V=
$p_2·V=<
Задача 5
Свинцовая пуля массой 10 г, летящая со скоростью 400 м/с, пробивает деревяный шар массой 1 кг, висящий на прочной нити, и вылетает из него со скоростью 300 м/с. Определите увеличение температуры пули после пробивания шара, если на её нагревание идёт 60% потери кинетической энергии системы «пуля–шар». Удельная теплоёмкость свинца $c=140$Дж/кг·С. Ответ выразите в кельвинах и округлите до десятых.
Решение
Количество теплоты, которое получает пуля равно: $Q=cm·∆t$(2), где $c$ - удельная теплоемкость свинца, $c=140$Дж/кг·С.
По условию задачи: $Q=0.6·∆E_к$, откуда $∆t=<0.6∆E_к>/
Задача 6
Два моля одноатомного газа, находящегося в цилиндре при температуре T1 = 200 К и давлении 2·10 5 Па, расширяется и одновременно охлаждается так, что его давление (p) в этом процессе обратно пропорционально объёму в кубе (V 3 ). Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A = 939,5 Дж, а его давление стало равным 0,25 · 10 5 Па?
Решение
1) Уравнение Менделеев-Клайперона: $pV=υRT$
Из уравнений Менделеева-Клапейрона для двух состояний газов: $
Значит газ отдал 2,8 кДж теплоты.
Задача 7
Два моля одноатомного газа, находящегося в цилиндре при температуре 400 К и давлении 4 · 10 5 Па, расширяются и одновременно охлаждаются так, что его давление в этом процессе обратно пропорционально объёму в кубе (V 3 ). Какую работу совершил газ при расширении, если он отдал количество теплоты 1979 Дж, а его давление стало равным 0,5 · 10 5 Па?
Решение
1) Первое начало термодинамики $-Q=∆U+A$, $∆U=<3>/<2>υRT$, по условию $p=<α>/ >$. 2) По закону Менделеева-Клайперона $pV=υRT$. 4) Таким образом $A=-Q-∆U=-1979-<3>/<2>·2·8.31(200-400)=5.5$кДж. 1 м 3 влажного воздуха при относительной влажности B = 60%, температуре T = 239 K и нормальном атмосферном давлении имеет массу M = 1,2004 кг. Определите давление насыщающего водяного пара при температуре T . В комнате размером V = 10 × 5 × 3 м 3 поддерживается температура T1 = 293 K, а точка росы равна T2 = 283 K. Определите относительную влажность воздуха и количество водяных паров, содержащихся в комнате. При $T=T_<расп>$ пар в комнате насыщенный $m=ρ·V=9.4·950=1.41$кг. Идеальный одноатомный газ расширяется сначала адиабатически, а затем изобарно так, что начальная и конечная температуры одинаковы. Работа, совершённая газом за весь процесс, равна 10 кДж. Какую работу совершил газ при адиабатическом расширении? Анализируя данные, составляем уравнение и выражаем ответ: Лазер излучает световые импульсы с энергией 200 мДж. Частота повторения импульсов 10 Гц. КПД лазера, определяемый отношением излучаемой энергии к потребляемой, составляет 4,0%. Какой объём воды нужно прокачать за один час через охлаждающую систему лазера, чтобы вода нагрелась не более чем на 5,0◦С? 1) Мощность излучения $P_<изл>=W·υ$. 2) Потребляемая мощность $P_л= 4) $Q_<охл>=P_<охл>·t$ выразим через числовой баланс $Q_<охл>=ρ·υ·c·∆t$ Стеклянная трубка, запаянная с одного конца, расположена горизонтально. Находящийся в трубке воздух отделён от атмосферы столбиком ртути длиной 11 см. Трубку перемещают вдоль её горизонтальной оси с постоянным ускорением, равным 8,6 м/с 2 , сначала запаянным концом вперёд, а затем открытым концом вперёд. В первом случае длина воздушного столбика в трубке оказалась в 1,3 раза больше, чем во втором. Определите атмосферное давление, считая температуру газа в трубке постоянной. Запишем уравнения для I и II случаев перемещения трубки: Тепловая машина с максимально возможным КПД имеет в качестве нагревателя резервуар с кипящей водой при температуре 100◦C, а в качестве холодильника — сосуд со льдом при температуре 0◦C. Какая масса льда растает при совершении машиной работы 1,22 МДж? Максимально возможный КПД достигается, если тепловая машина работает по циклу Карно. Он равен: $η= Отданная холодильнику теплота расходуется на таяние льда при температуре плавления. Следовательно, $|Q_<отд>|=mλ$(7). Приравняем (6) и (7): $mλ= За один цикл идеальная тепловая машина совершает работу, составляющую 25 кДж. При изотермическом сжатии работа внешних сил равна 20 кДж. Определите отношение температуры нагревателя к температуре холодильника. КПД идеальной тепловой машины определяется выражением: $η= При изотермическом сжатии работа внешних сил равна 20кДж, значит, в этом процессе газ отдает тепло холодильнику. Согласно 1 закону термодинамики $Q_х=-A'+0$ и значит, $A′=|Q_x|$. Тогда найдем $Q_н$ - количество теплоты, полученное от нагревателя: $Q_н=A+|Q_x|=A+A′=25+20=45кДж.$ Подставим числовые значения в (2) и найдем $ Горизонтально расположенный закрытый цилиндрический сосуд длиной 0,6 м с гладкими стенками, разделённый на две части тонким подвижным теплонепроницаемым поршнем, заполнен идеальным газом. В начальный момент объём левой части вдвое больше объёма правой, а температура в обеих частях одинакова. Температуру газа в правой части увеличили вдвое, а в левой поддерживают постоянной. Найдите перемещение поршня. Ответ выразите в (см). Приведем рисунок для решения задачи, причем условимся писать все величины, соответствующие начальному моменту времени, писать без «звездочки», а конечному — со «звездочкой». Так как поршень и в начальный, и в конечный момент времени будет находиться в равновесии, то можно записать первый закон Ньютона и два уравнения Клапейрона-Менделеева. Из первой строки системы видно, что давления газов равны, те. $р_1 = р_2 = р$. Зная, что по условию $V_1=2V_2$ и $T_1= T_2 = Т$, получим: Поделив верхнее выражение на нижнее, имеем: $<υ_1>/<υ_2>=2$. Отлично, мы нашли отношение количества молей газов в левой и правой части сосуда. Теперь повторим то же самое и для конечного момента времени, те. опять запишем первый закон Ньютона и два уравнения Клапейрона-Менделеева: Опять видно, что $р_1* =р_2* = р*$. Теперь разберемся с температурами. Так как $Т_2* = 2Т_2 = 2Т$ и $Т_1*=Т_1=Т$, то очевидно, что их отношение равно $<Т_2*>/<Т_1*>=2$. Тогда: Значит поршень в конце разделит сосуд на две равные части. Для того, чтобы узнать на сколько сместиться поршень, следует заметить такой факт: $ В задаче считается, что поршень имеет нулевую толщину. В этой формуле $V$ — это общий объем сосуда, равный $V = V_1 + V_2$, тогда: $ Перемещение поршня можно найти по формуле: $∆l=l_1-l_1*=<2>/<3>L-<1>/<2>L=<1>/<6>L; ∆l=<0.6>/<6>=0.1м$.Задача 8
Решение
Задача 9
Решение
Задача 10
Решение

Задача 11
Решение
Задача 12
Решение
Задача 13
Решение
Задача 14
Решение
$Задача 15
Решение

§ 3.12. Примеры решения задач
Если изменяются все три параметра, то следует воспользоваться уравнением состояния в форме (3.9.9) или (3.9.5).
Как измерить медицинским термометром температуру тела человека, если температура окружающего воздуха +42 °С?
Решение. Можно предварительно охладить термометр в холодильнике. Если холодильника нет, то нужно подержать термометр 5—8 мин под мышкой, извлечь его и сразу же стряхнуть. Термометр покажет температуру тела, так как ртуть в термометре сожмется при контакте с телом до объема, соответствующего температуре тела.
Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно р. Определите давление р1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
Решение. При горизонтальном положении цилиндра объем каждой его части обозначим через V (эти объемы равны). При вертикальном положении цилиндра объем верхней части станет равным V + ΔV, а нижней V - ΔV. Давление в нижней части цилиндра станет равным . Согласно закону Бойля— Мариотта

Исключив из этих равенств , получим квадратное уравнение для p1:


Второй корень квадратного уравнения отрицателен и потому лишен физического смысла.
Поршневой насос при каждом качании захватывает воздух объемом V0. При откачке этим насосом воздуха из сосуда объемом V насос совершил п качаний. Затем другой насос с тем же рабочим объемом V0 начал нагнетать воздух из атмосферы в тот же сосуд, совершив также п качаний. Какое давление установится в сосуде? Температуру воздуха во время работы насоса считать постоянной.
Решение. Согласно закону Бойля—Мариотта при откачке воздуха из сосуда после первого качания давление в сосуде станет равным , где p0— атмосферное давление.
После второго качания будет выполняться равенство p1V = p2(V + V0) и, следовательно, и т.д. После n качаний в сосуде установится давление
При нагнетании воздуха в сосуд после n качаний давление станет равным

При любом n р > р0, так как во время нагнетания воздуха при каждом качании насос захватывает воздух, имеющий атмосферное давление р0, а при откачке при каждом качании удаляется воздух при давлении, меньшем р0.
В запаянной с обоих концов цилиндрической трубке находится воздух при нормальных условиях. Трубка разделена подвижным поршнем на две части, объемы которых V1 и V2 относятся как 1 : 2. До какой температуры t1 следует нагреть воздух в меньшей части трубки и до какой t2 охладить в большей, чтобы поршень делил трубку на две равные части, если нагревание и охлаждение в обеих частях трубки производятся при условии = const?
Решение. Условие = const означает, что процессы нагревания и охлаждения происходят изобарно. При отношении начальных объемов эти объемы составляют и , где V0 — объем всей трубки. Конечные объемы обеих частей одинаковы и равны .
Согласно закону Гей-Люссака для воздуха в меньшей части трубки выполняется соотношение
а для воздуха в большей части
где Т0 = 273 К — температура, соответствующая начальным условиям. Отсюда

В цилиндре под поршнем находится воздух при давлении p1 = 2 • 10 5 Па и температуре t1 = 27 °С. Определите массу m груза, который нужно положить на поршень после нагревания воздуха до температуры t2 = 50 °С, чтобы объем воздуха в цилиндре стал равен первоначальному. Площадь поршня S = 30 см 2 .
Решение. Так как в процессе нагревания объем воздуха в цилиндре не изменяется, то согласно закону Шарля имеем

Подставляя в (3.12.1) выражение для р2, получим

Найдите среднюю (эффективную) молярную массу сухого атмосферного воздуха, предполагая известный процентный состав воздуха по массе: азот — n1 = 75,52%, кислород — n2 = 23,15%, аргон — n3 = 1,28% и углекислый газ — n4 = 0,05%.
Решение. Для каждого газа можно записать уравнение состояния:

Здесь M1, M2, M3 и M4 — молярные массы соответственно азота, кислорода, аргона и углекислого газа.
Складывая правые и левые части этих уравнений, получим

Для смеси газов выполняется соотношение
где m = m1 + m2 + m3 + m4 — масса воздуха с объемом V, а М — искомая эффективная молярная масса. Согласно закону Дальтона
Сравнивая уравнения состояния (3.12.2) и (3.12.3), получим

Разделив числитель и знаменатель на m и умножив на 100%, получим выражение для М через процентный состав воздуха по массе

Закрытый с обоих концов цилиндр наполнен газом при давлении p = 100 кПа и температуре t = 30 °С и разделен подвижным теплонепроницаемым поршнем на две равные части длиной L по 50 см. На какую величину ΔT нужно повысить температуру газа в одной половине цилиндра, чтобы поршень сместился на расстояние l = 20 см, если во второй половине цилиндра температура не изменяется? Определите давление газа после смещения поршня.
Решение. Для газа в части цилиндра с постоянной температурой применим закон Бойля—Мариотта:

где S — площадь основания цилиндра. Для нагреваемой части цилиндра запишем уравнение Клапейрона:

В уравнениях (3.12.4) и (3.12.5) р1 — давление газа после смещения поршня, одинаковое в обеих частях цилиндра вследствие равновесия поршня, а Т + ΔT в уравнении (3.12.5) — температура газа в нагретой части цилиндра.
Разделив почленно уравнение (3.12.4) на уравнение (3.12.5), получим
Из уравнения (3.12.4) находим p1:
Сосуд объемом V = 100 л разделен пополам полупроницаемой перегородкой. В начальный момент времени в одной половине сосуда находился водород, масса которого m1 = 2 г, а во второй — 1 моль азота. Определите давления, установившиеся по обе стороны перегородки, если она может пропускать только водород. Температура в обеих половинах одинакова и постоянна: t = 127 °С.
Решение. Так как водород свободно проходит через перегородку, то он распространяется по всему сосуду. Запишем уравнение Менделеева—Клапейрона для водорода после установления состояния равновесия:
где М1 = 2 • 10 -3 кг/моль — молярная масса водорода.
В той части сосуда, в которой вначале был только водород, он и в дальнейшем останется в чистом виде, так что давление в этой части сосуда станет равным

Для азота уравнение Менделеева—Клапейрона имеет вид
где р2 — давление азота.
Так как в этой половине находятся водород и азот, то полное давление р согласно закону Дальтона складывается из парциальных давлений р1 и р2, т. е.

Гелий массой 20 г, заключенный в теплоизолированном цилиндре под поршнем, медленно переводится из состояния 1 с объемом V1 = 32 л и давлением р1 = 4,1 атм в состояние 2 с объемом V2 = 9 л и давлением р2 = 15,5 атм. Какой наибольшей температуры достигнет газ при этом процессе, если на графике зависимости давления газа от объема процесс изображается прямой линией (рис. 3.18)?

Решение. Как следует из рисунка 3.18, давление и объем газа связаны линейной зависимостью: р = aV + b, где а и b — постоянные коэффициенты. Из условий задачи получаем систему уравнений

Решив эту систему относительно а и b, найдем

Подставив в уравнение Менделеева—Клапейрона вместо р выражение aV + b, получим

График зависимости Т от V представляет собой параболу (рис. 3.19).

Кривая достигает максимума при Vmax = = 20 л, когда корни квадратного уравнения (3.12.6) совпадают. При этом


На рисунке 3.20 изображен график изменения состояния идеального газа в координатах р, V. Начертите графики этого процесса в координатах V, Т и р, Т.

Решение. Из рисунка 3.20 следует, что давление газа р и его объем V находятся в прямой пропорциональной зависимости
где k — постоянный коэффициент. Подставив значение давления (3.12.7) в уравнение Менделеева— Клапейрона, получим

Уравнение (3.12.8) — это уравнение параболы, ось симметрии которой совпадает с осью Т. Следовательно, в координатах V, Т искомый график имеет вид, показанный на рисунке 3.21, а. Аналогично получим график этого процесса в координатах p, T (рис. 3.21, б).

- Вы надули щеки. При этом и давление, и объем воздуха во рту увеличиваются. Как это согласуется с законом Бойля— Мариотта?
- Чтобы измерить температуру человеческого тела, приходится держать термометр под мышкой в течение 5—8 мин. В то же время стряхнуть его можно практически сразу после измерения температуры. Почему?
- Узкая вертикальная трубка длиной L, закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути длиной h. Плотность ртути равна ρ. Трубка расположена открытым концом вверх. Какова была длина l столбика воздуха в трубке, если при перевертывании трубки открытым концом вниз из трубки вылилась половина ртути? Атмосферное давление равно р0.
- В ртутный барометр попал пузырек воздуха, вследствие чего барометр показывает давление меньше истинного. При давлении р1 = 768 мм рт. ст. уровень ртути расположен на высоте h1 = 748 мм, причем длина пустой части трубки l = 80 мм. Каково атмосферное давление р2, если ртуть стоит на высоте h2 = 734 мм? Плотность ртути ρ = 1,36 • 10 4 кг/м 3 .
- Площадь сечения цилиндра автомобильного насоса S = 10 см 2 . Определите длину l цилиндра, если известно, что для накачки шины объемом V = 0,02 м 3 от давления р0 = 1 • 10 5 Па до давления р = 3 • 10 5 Па требуется совершить n = 100 качаний. Утечкой и нагреванием воздуха пренебречь.
- В цилиндре под поршнем находится воздух. Поршень имеет форму, показанную на рисунке 3.22. Масса поршня m = 6 кг, площадь сечения цилиндра S = 20 см 2 . Атмосферное давление р0 = 10 5 Па. Найдите массу m1 груза, который надо положить на поршень, чтобы объем V1 воздуха в цилиндре уменьшился в 2 раза. Трение не учитывать. Температура постоянна.
Читайте также:

