два моля одноатомного газа находящегося в цилиндре при температуре 200 к и давлении
9. Термодинамика
Некоторое число молей одноатомного идеального газа расширяется изотермически из состояния \(p_1 = 10^5\) Па и \(V_1 = 1\) литр до объема \(V_2 = 2V_1\) . Чему равно изменение внутренней энергии этого газа? (Ответ дайте в джоулях.)
Изменение внутренней энергии равно: \[\Delta U=\dfrac<3><2>\nu R\Delta T,\] где \(\nu\) — количество вещества газа, \(R\) — универсальная газовая постоянная, \(\Delta T\) — изменение абсолютной температуры газа.
По условию задачи процесс изотермический, следовательно: \[T_1=T_2=const \hspace <2 mm>\Rightarrow \hspace <2 mm>\Delta T=0\] Подставим в формулу: \[\Delta U=\dfrac<3><2>\nu R\cdot0\] Получим, что изменение внутренней энергии также равно нулю: \[\Delta U=0\]
В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 8 раз, давление воздуха в сосуде увеличилось в 2 раза, а его абсолютная температура увеличилась в 1,5 раза. Во сколько раз уменьшилась внутренняя энергия газа в сосуде? (Воздух считать идеальным газом.)
Внутренняя энергия газа равна: \[\hspace <4 mm>U=\dfrac<2>\nu RT, \hspace <4 mm>(1)\] где \(\nu\) — количество вещества газа, \(R\) — универсальная газовая постоянная, \(T\) — абсолютная температура газа, \(i\) — число степеней свободы.
Запишем уравнение Менделеева – Клапейрона: \[\hspace <4 mm>pV=\nu RT, \hspace <4 mm>(2)\] где \(p\) — давление газа, \(V\) — объем, занимаемый газом.
Из (2) выразим \(\nu RT= pV\) и подставим в (1), получим: \[\hspace <4 mm>U=\dfrac<2>pV \hspace <4 mm>(3)\] Запишем (3) для первого и второго состояния с учетом того, что по условию \(V_2=\dfrac<1><8>V_1\) и \(p_2=2p_1\) : \[U_1 = \dfrac<2>p_1V_1 \hspace <10 mm>U_2 = \dfrac<2>p_2V_2\] \[\hspace <10 mm>U_1 = \dfrac<2>p_1V_1 \hspace <10 mm>U_2 = \dfrac<2>\cdot2p_1\cdot\dfrac<1><8>V_1\] Найдем, во сколько раз уменьшилась внутренняя энергия газа: \[\dfrac
В процессе адиабатного сжатия двух молей идеального одноатомного газа внешние силы совершили работу 575 Дж. Определите изменение температуры данной порции газа в результате этого процесса. (Ответ дайте в кельвинах и округлите до целых).
При адиабатном процессе количество теплоты равно нулю: \(Q=0\) .
Запишем первое начало термодинамики: \[Q=\Delta U+A,\] где \(\Delta U\) — изменение внутренней энергии газа, \(A\) — работа газа. Для адиабатного процесса имеем: \[\Delta U = -A\] Работа внешних сил равна: \[A_\text <внеш. сил>= -A\] С учетом этого получаем, что: \[\hspace <5 mm>\Delta U = A_\text <внеш. сил>\hspace <5 mm>(1)\] Изменение внутренней энергии газа равно: \[\hspace <5 mm>\Delta U=\dfrac<2>\nu R\Delta T, \hspace <5 mm>(2)\] где \(\nu\) — количество вещества газа, \(R\) — универсальная газовая постоянная, \(\Delta T\) — изменение абсолютной температуры газа, \(i\) — число степеней свободы (так как газ одноатомный, то \(i = 3\) ).
Приравняем (1) и (2) и выразим изменение температуры газа: \[\dfrac<3><2>\nu R\Delta T=A_<\text<внеш.сил>>\] \[\Delta T = \dfrac<2><3>\cdot\dfrac
Во сколько раз изменяется внутренняя энергия идеального газа при повышении его температуры в 2 раза при неизменном объеме?
Изменение внутренней энергии газа равно: \[\Delta U=\dfrac<2>\nu R \Delta T,\] где \(\nu\) — количество вещества газа, \(R\) — универсальная газовая постоянная, \(T\) — абсолютная температура газа, \(i\) — число степеней свободы.
Изменение внутренней энергии газа прямо пропорционально изменению его температуры. Так как температура газа увеличилась в 2 раза, то и внутренняя энергия газа изменилась в 2 раза.
Одноатомный идеальный газ в количестве одного моля совершает работу, равную 2700 Дж, при этом к газу было подведено количество теплоты, равное 3,2 кДж. Начальная температура газа равна \(T_1 = 100^\circ\) С . Чему равна конечная температура \(T_2\) ? (Ответ дайте в градусах Цельсия и округлите до целых).
Первое начало термодинамики: \[Q=\Delta U+A,\] где \(Q\) — количество теплоты, \(\Delta U\) — изменение внутренней энергии газа, \(A\) — работа газа. Выразим изменение внутренней энергии газа: \[\hspace <5 mm>\Delta U=Q-A \hspace <5 mm>(1)\] Изменение внутренней энергии газа равно: \[\Delta U=\dfrac<2>\nu R \Delta T,\] где \(\nu\) — количество вещества газа, \(R\) — универсальная газовая постоянная, \(\Delta T\) — изменение абсолютной температуры газа, \(i\) — число степеней свободы (так как газ одноатомный, то \(i = 3\) ).
Выразим изменение температуры: \[\hspace <5 mm>\Delta T=\dfrac<2><3>\cdot\dfrac<\Delta U> <\nu R>\hspace <5 mm>(2)\] Подставим (1) в (2): \[\Delta T = \dfrac<2><3>\cdot\dfrac
Один моль аргона, находящийся в цилиндре при температуре \(T_1=600\) К и давлении \(p_1=4\cdot10^5\) Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа \(p_2=1\cdot10^5\) Па. Чему равна внутренняя энергия газа после расширения? (Ответ дайте в джоулях.)
По условию температура газа при расширении обратно пропорциональна объёму: \[T\sim \dfrac<1>
Внешними силами над идеальным одноатомным газом, количество которого равно 1,5 моля, совершена работа, равная 3600 Дж, при этом температура газа увеличилась на 230 \(^<\circ>\) C. Чему равно количество теплоты \(Q\) , полученное газом в этом процессе? (Ответ дайте в Дж и округлите до целого числа.)
Первое начало термодинамики: \[\hspace <5 mm>Q=\Delta U+A \hspace <5 mm>(1)\] где \(Q\) — количество теплоты, \(\Delta U\) — изменение внутренней энергии газа, \(A\) — работа газа.
Изменение внутренней энергии газа равно: \[\hspace <5 mm>\Delta U=\dfrac<2>\nu R \Delta T \hspace <5 mm>(2)\] где \(\nu\) — количество вещества газа, \(R\) — универсальная газовая постоянная, \(\Delta T\) — изменение абсолютной температуры газа, \(i\) — число степеней свободы (так как газ одноатомный, то \(i = 3\) ).
Подставим (2) в (1): \[Q= \dfrac<3><2>\nu R \Delta T +A\] Работа внешних сил равна: \[A_\text <внеш. сил>= -A\] С учетом этого получаем, что: \[Q= \dfrac<3><2>\nu R \Delta T - A_\text<внеш. сил>\] Подставим известные значения (с учетом того, что изменение температуры в градусах Цельсия и Кельвина одинаково): \[Q=\dfrac<3><2>\cdot1,5\text< моль>\cdot8,31\text< Дж/( моль$\cdot$ К)>\dfrac<\text<Дж>><\text<моль>\cdot\text<К>>\cdot230\text< К>-3600\text< Дж>\approx 700 \text< Дж>\]
Станкиновские олимпиады
Решение. Задачу просто решить, если построить график зависимости скорости поезда от времени. Тогда путь равен площади трапеции:
2. На наклонной плоскости находится тело массой m = 10 кг, на которое действует горизонтально направленная сила F = 100 Н. Определите ускорение тела и силу, с которой оно давит на плоскость. Наклонная плоскость составляет с горизонтом угол a = 30°. Коэффициент трения скольжения между телом и плоскостью m = 0,2.
N = mg cos a – F sin a » 34,9 Н.
Решение. Так как V1 = V2, то, по закону Шарля:
Решение. Найдем зависимость p(V) c помощью уравнения Менделеева–Клапейрона:
Построим график зависимости p(V) и отметим на нем значения давления и объема, соответствующие начальной и конечной температурам. Работа, совершенная газом, определится площадью трапеции, ограниченной прямой ординатами p1 и p2, а также осью V:
5. В однородном электростатическом поле, направленном вертикально вниз, равномерно вращается заряженный шарик массой m и зарядом q > 0, подвешенный на нити длиной l. Угол отклонения нити от вертикали при вращении шарика в горизонтальной плоскости равен a . Найдите кинетическую энергию этого шарика.
1. При какой угловой скорости вращения w планеты вокруг оси, проходящей через ее центр масс, линия отвеса на любой широте параллельна оси вращения? Масса планеты M, радиус планеты R, гравитационная постоянная G. Плотность планеты считается постоянной.
Решение. Уравнение движения тела массой m на подвесе на широте q есть уравнение движения тела по окружности радиусом R cos q с угловой скоростью w под действием равнодействующей силы тяжести Fт и силы натяжения нити подвеса T.
Тогда:
[Отметим, что если точка подвеса находится точно в плоскости экватора, приведенное рассмотрение неприменимо. – Ред.]
2. При температуре t1 = 15 °С в стальном баллоне объемом 10 л давление водорода 1,3 • 10 7 Па. Через некоторое время часть газа вытекла, и при температуре t2 = 20 °C давление составило 1,2 • 10 7 Па. Определите массу вытекшего из баллона водорода.
3. От источника тока необходимо передавать потребителю, работающему при напряжении U0 = 10 В, мощность N0 = 5 Вт. Каким должно быть сопротивление подводящих проводов, чтобы потери мощности в них составили 5 % от мощности потребителя? Какое напряжение будет на зажимах источника?
4. В схеме, изображенной на рисунке, индуктивности катушек равны L1 и L2, а конденсатор C заряжен до напряжения U0. Определите максимальные токи I1 и I2, протекающие через катушки 1 и 2 соответственно после замыкания ключа К. Сопротивлением катушек и проводов можно пренебречь.
Решение. Согласно закону сохранения энергии:
Катушки и конденсатор соединены параллельно, поэтому:
При максимальных токах E1 инд = E2 инд = U = 0, отсюда:
5. Предмет длиной a расположен вдоль главной оптической оси собирающей линзы, между центром линзы и ее фокусом, на расстоянии b от фокуса линзы. Во сколько раз k отличается длина изображения предмета от его длины a, если линза имеет фокусное расстояние F?
Два моля одноатомного газа находящегося в цилиндре при температуре 200 к и давлении
2011 год 109 вариант СЗ
В сосуде лежит кусок льда. Температура льда t1 = 0°С. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20°С? Тепловыми потерями на нагрев сосуда пренебречь. (Решение)
2011 год. 01-2 вариант. С3
В бутылке объемом V = 1 л находится гелий при нормальном атмосферном давлении. Горлышко бутылки площадью S = 2 см 2 заткнуто короткой пробкой, имеющей массу m = 20 г. Если бутылка лежит горизонтально, то для того, чтобы медленно вытащить из ее горлышка пробку, нужно приложить к пробке горизонтально направленную силу F = 1 Н. Бутылку поставили на стол вертикально горлышком вверх. Какое количество теплоты нужно сообщить гелию в бутылке для того, чтобы он выдавил пробку из горлышка? (Решение)
2011 год. 01-1 вариант. С3
Один моль идеального одноатомного газа переводят из состояния 1 с температурой Т1 = 300 К в состояние 2 таким образом, что в течение всего процесса давление газа возрастает прямо пропорционально его объему. В ходе этого процесса газ получает количество теплоты Q = 14958 Дж. Во сколько раз n уменьшается в результате этого процесса плотность газа? (Решение)
2010 год. 11 вариант. С1
В кабинете физики проводились опыты с разреженным газом постоянной массы. По невнимательности ученик, отметив на графике начальное и конечное состояния газа (см. рисунок), не указал, какие две величины из трёх (давление р, объём V, температура Т) отложены по осям. В журнале осталась запись, согласно которой названные величины изменялись следующим образом: p1 < р2, V1 > V2, Τ1 < Ί2. Пользуясь этими данными, определите, какие величины были отложены на горизонтальной и вертикальной осях. Ответ поясните, указав, какие физические закономерности вы использовали. (Решение)
2010 год 304 вариант СЗ
Некоторое количество одноатомного идеального газа расширяется из одного и того же начального состояния (p1, V1) до одного и того же конечного объёма V2 первый раз по изобаре, а второй - по адиабате (см. рисунок). Отношение количества теплоты Q12, полученного газом на изобаре от нагревателя, к модулю изменения внутренней энергии газа |U3 — U1| на адиабате k = Q12/|U3 — U1| = 6 . Чему равно отношение х работы газа на изобаре А12 к работе газа на адиабате А13? (Решение)
2010 год. 135 вариант. С5
В цилиндр закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие площадью 5·10 -4 м 2 , закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии невесомым стержнем длиной 0,5 м, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). Расстояние АВ равно 0,1 м. К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите объём цилиндра. (Решение)
2009 год. 133 вариант. С1
В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают вдвигать в сосуд. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните. (Решение)
2009 год. 133 вариант. С3
Один моль одноатомного идеального газа переходит из состояния 1 в состояние 3 в соответствии с графиком зависимости его объёма V от температуры T (T0 = 100 К). На участке 2 − 3 к газу подводят 2,5 кДж теплоты. Найдите отношение работы газа А123 ко всему количеству подведенной к газу теплоты Q123. (Решение)
2009 год. 304 вариант. С3
Постоянная масса одноатомного идеального газа совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты QH = 8 кДж. Какую работу совершают внешние силы при переходе газа из состояния 2 в состояние 3? (Решение)

2008 год. 131 вариант. С2
Разогретый сосуд прикрыли поршнем, который с помощью вертикальной нерастяжимой нити соединили с потолком. На сколько процентов от начальной понизится температура воздуха в сосуде к моменту, когда сосуд оторвется от поверхности, на которой он расположен? Масса сосуда 5 кг. Поршень может скользить по стенкам сосуда без трения. Площадь дна сосуда 125 см 2 . Атмосферное давление 10 5 Па. Тепловым расширением сосуда и поршня пренебречь. (Решение)
2008 год. 5941 вариант. С2
В калориметре находился m1 = 1 кг льда при температуре t1 = -5°С. После добавления в калориметр m2 = 25 г воды в нем установилось тепловое равновесие при температуре t = 0°С. Какова температура t2 добавленной в калориметр воды, если в калориметре оказался в итоге только лёд? Теплоёмкостью калориметра пренебречь. (Решение)
2008 год. 05205939 вариант. С2
В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз. На сколько градусов следует нагреть воздух в трубке, чтобы объём, занимаемый воздухом, стал прежним? Температура воздуха в лаборатории 300 К, а атмосферное давление составляет 750 мм рт.ст. (Решение)
2008 год. 2 вариант. С2
Вертикально расположенный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество водорода при температуре 361 К. Какая масса газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь. (Решение)
2007 год. 19 вариант. С2
В сосуде находится одноатомный идеальный газ, масса которого 12 г, а молярная масса 0,004 кг/моль. Вначале давление в сосуде было равно 4•10 5 Па при температуре 400 К. После охлаждения газа давление понизилось до 2•10 5 Па. Какое количество теплоты отдал газ? (Решение)
2006 год. 61 вариант. С2
В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м, закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объём воздуха в мешке достигает 28,0 м 3 - мешок всплывает вместе с прикреплённым к нему грузом. Масса оболочки мешка 2710 кг. Определите массу груза. Температура воды равна 7°С, атмосферное давление на уровне моря равно 10 5 Па. Объёмом груза и стенок мешка пренебречь. (Решение)
2006 год. 86 вариант. С2
Теплоизолированный сосуд объемом V = 2 м 3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль гелия, а в другой - такое же количество молей аргона. Начальная температура гелия равна 300 К, а температура аргона 600 К. Определите давление смеси после удаления перегородки. Теплоемкостью сосуда пренебречь. (Решение)
2006 год. 33 вариант. С2
Воздушный шар объемом 2500 м 3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м 3 . При какой минимальной разности температур воздуха внутри шара и снаружи шар взлетит вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Оболочку шара считать нерастяжимой. (Решение)
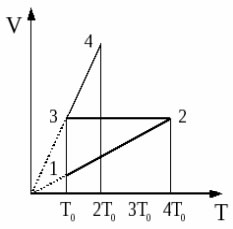
2006 год. 222 вариант. С2
С одним молем идеального одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке в координатах V-Т. Во сколько раз количество теплоты, полученное газом в процессе 1-2-3-4, больше работы газа в этом процессе? (Решение)
2005 год. 58 вариант. С2
Идеальный одноатомный газ в количестве 1 моль сначала изотермически расширился при температуре T1 = 300 К. Затем газ изобарно нагрели, повысив температуру в 3 раза. Какое количество теплоты получил газ на участке 2-3? (Решение)
2004 год. 92 вариант. С2
10 моль одноатомного идеального газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты получил газ на участке 2-3? (Решение)
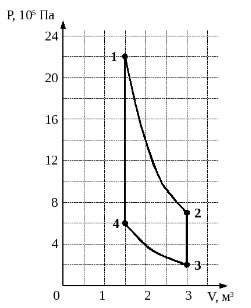
2004 год. 77 вариант. С5
Идеальный одноатомный газ используется в качестве рабочего тела в тепловом двигателе. В ходе работы двигателя состояние газа изменяется в соответствии с циклом, состоящим из двух адиабат и двух изохор (см. рисунок). Вычислите КПД такого двигателя. (Решение)
2004 год. 49 вариант. С5
При электролизе воды образуется кислород О2 и водород Н2. Газы отводят в сосуд объёмом 100 л, поддерживая в нём температуру 300 К. Чему равна масса воды, которая разложилась в результате электролиза, чтобы суммарное давление в сосуде достигло 0,1 атм? Считать, что ничего не взрывается. (Решение)
2004 год. 35 вариант. С5
Смесь одинаковых масс гелия, водорода и азота помещена в сосуд и нагрета до температуры 350 К. Плотность смеси оказалась равной 50 г/м 3 . Чему равно давление в сосуде? (Решение)
Гелий – одноатомный газ, и для него
Решение.
Так как газ получает тепло от нагревателя лишь на участке 1-2,
Подставляя эти выражения, получим A = А12=3/2 RDТ/(1-h).
5. К идеальному одноатомному газу, заключенному внутри масляного пузыря, подводится тепло. Найти молярную теплоемкость этого газа, если давлением снаружи можно пренебречь. ( МФТИ, до1992г)
Ответ: С = 3R
Решение.
Воспользуемся 1-ым началом термодинамики:
Если радиус пузыря r , давление газа в пузыре по формуле Лапласа равно
объем газа V = 4/3pr 3 , так что
Для одноатомного газа
PV =RT т.е. (4s/r)(4/3pr 3 ) = RT
Изменяя r на малую величину и пренебрегая членом с (Dr) 2 , получаем, что 32/3psrDr = RDT ,
Подставляя это соотношение в первое начало, получаем
С = Сv + (4s/r) 4pr 2 3R/(32psr) = Сv + 3/2R = 3R
6. Два сосуда заполнены одним и тем же идеальным газом и сообщаются при помощи узкой трубки. Отношение объемов сосудов V1/V2 = 2 . Первоначально газ в первом сосуде имел температуру Т1 = 300К. В результате перемешивания происходит выравнивание температур. Найти первоначальную температуру газа во втором сосуде, если конечная температура Т = 350К. Теплообменом газов со стенками сосудов и трубки пренебречь.
Ответ: Т2 = 525К.
Решение.
Система, состоящая из газов в обоих сосудах, работы над другими телами не производит и теплом с окружающими телами не обменивается. Следовательно, внутренняя энергия системы сохраняется:
Подставив эти выражения в первое уравнение, получим после упрощений
Решение.
Рассмотрим систему из двух газов. Оба газа двухатомные. У них постоянная теплоемкость при постоянном объеме Сv . Система из двух газов тепла от других тел не получает и работы над телами, не входящими в систему, не совершает. Поэтому внутренняя энергия системы сохраняется:
Отсюда температура смеси
Решение.
Удельная теплоемкость в данном процессе
По первому закону термодинамики

Ответ: m = 22г.
Решение.
При конденсации пара массой m при 100 о С выделяется количество теплоты
При охлаждении получившейся воды до t = 40 o C выделяется количество теплоты
При нагревании льда от t1 = -10 o C до to = 0 o C поглощается количество теплоты
При плавлении льда поглощается количество теплоты
При нагревании получившейся воды от to до t поглощается количество теплоты
Для нагревания калориметра от t1 до t требуется количество теплоты
По закону сохранения энергии
Решение.
По определению КПД тепловой машины
где АП – полная работа газа за цикл (площадь цикла в координатах P,V), а QH – тепло, получаемое рабочим газом извне (от нагревателя). Согласно первому началу термодинамики работа на адиабате 1-2
Работа на изотерме по условию А23 = -А, работа на изохоре А31 = 0. Таким образом, полная работа газа за цикл равна
т.к. Т1 и Т2 и есть максимальная и минимальная температуры в цикле. Итак,
т.к. Сv = 3/2R (газ одноатомный).
11. Над идеальным газом постоянной массы проводится циклический процесс, состоящий из двух изобар и двух изохор, как показано на рисунке. Заданы значения давлений Р1 и Р2 и температуры Т2. При каком соотношении температур Т2 и Т4 полная работа за цикл больше: в случае Т4 > Т2 или Т4 < Т2 ?(МГУ,1999)
Решение.
Работа за цикл равна
Из уравнения Клапейрона-Менделеева:
Следовательно, работа за цикл будет больше, если Т4 > T2.
P 2 ) от начального значения Т1 = 300К до конечного
Т2 = 400К. Определить работу, совершаемую газом в этом процессе, и количество подведенного к нему тепла.
Решение.
Нарисуем график процесса в координатах Р, V. Из уравнения состояния идеального газа
где k = const, получаем
т.е. уравнение прямой, проходящей через начало координат. Работа газа равна заштрихованной площади трапеции:
Количество тепла найдем из первого закона термодинамики:
Решение.
Нарисуем цикл в координатах Р, V (см. рис.);
минимальная температура – T1, максимальная Т3 ,
Работа за цикл равна площади цикла
Решение.
Уравнение состояния газа запишется в виде
Подставляя полученные соотношение в первое начало термодинамики, запишем
15. Моль идеального газа нагревается при постоянном давлении, а затем при постоянном объеме переводится в состояние с температурой, равной начальной То = 300К. Оказалось, что в итоге газу сообщено количество теплоты Q = 5кДж. Во сколько раз изменился объем, занимаемый газом?
Ответ: n = Q/RTo + 1
Решение.
Нарисуем график процесса в координатах
P – V (см. рис.). Пусть конечный объем равен nVo. Тогда, т.к. 1 – 2 – изобара, температура в точке 2 равна nTo.
Ответ: Т2 = 312.8К
Решение.
Вычитая из второго уравнения первое, получим
Решение.
Работу, совершенную паровой машиной можно определить как
где N – мощность машины. Паровая машина отдает количество теплоты
где m – масса сгоревшего угля. Тогда
КПД идеальной тепловой машины, работающей по циклу Карно
Решение.
КПД реального теплового двигателя определяет формула
где Q1 – количество теплоты, переданной нагревателем рабочему веществу в процессе его изохорного нагревания, которому соответствует участок 1 – 2, Q2 – количество теплоты, переданной газом холодильнику в процессе его изохорного охлаждения, чему соответствует участок 3 – 4. При изохорных процессах работа А = 0, тогда согласно первому закону термодинамики
где в соответствии с уравнением Менделеева-Клайперона при изохорных процессах
Максимальный КПД идеального теплового двигателя определяется формулой
где Т1 – абсолютная температура нагревателя, Т2 – абсолютная температура холодильника. Если в состоянии 2 газ находится в тепловом равновесии с нагревателем, то его температура в этом состоянии равна температуре нагревателя Т1 . Аналогично, если в состоянии 4 газ оказался в тепловом равновесии с холодильником, то его температура в этом состоянии равна температуре холодильника Т2 , т.е. в состоянии 4 температура газа стала равна Т2. Для нахождения температур Т1 и Т2 воспользуемся уравнением Менделеева-Клайперона, применив его к состояниям газа 2 и 4:
После этого для КПД идеального двигателя получим
19. В горизонтальном неподвижном цилиндрическом сосуде, закрытом поршнем, площадь сечения которого равна S, находится один моль газа при температуре То и давлении Ро (см. рис.). Внешнее давление постоянно и равно Ро. Газ нагревают внешним источником теплоты. Поршень начинает двигаться, причем сила трения скольжения равна f. Найти зависимость температуры газа Т от получаемого им от внешнего источника количества теплоты, если в газ поступает еще и половина количества теплоты, выделяющегося при трении поршня о стенки сосуда. Построить график этой зависимости. Внутренняя энергия одного моля газа U = cT. Теплоемкостью сосуда и поршня пренебречь. (Меледин, 2.65)
Решение.
Пока поршень покоится, вся теплота идет на нагрев газа:
Найдем, используя условие равновесия и закон Шарля, критическую температуру Ткр, при превышении которой поршень начнет двигаться:
32. Работа газа. Первое начало термодинамики: задачи с ответами без решений
(Все задачи по молекулярно-кинетической теории и ответы к ним находятся в zip-архиве (290 кб), который можно скачать и открыть на своем компьютере. Попробуйте решить задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)
32.1. Какова внутренняя энергия одноатомного газа, занимающего при температуре T объем V, если концентрация молекул n? [ U = (3/2)nkTV ]
32.2. В цилиндре с площадью основания S = 100 см 2 находится газ при температуре t = 27 °С. На высоте h = 30 см от дна цилиндра расположен поршень массой m = 60 кг. Какую работу совершит газ, если его температуру медленно повысить на Δt = 50 °С? Атмосферное давление po = 10 5 Па. [ A ≅ 79.4 Дж ]
32.3. Газообразный водород массой m = 0,1 кг совершает круговой процесс 1 – 2 – 3 – 1 (рис.). Найдите работу газа на участке 1 – 2, если Т1 = 300 K, a V2 = 3V1. [ A = 2.5×10 5 Дж ]
32.4. Идеальный газ массой m = 20 г и молярной массой M = 28 г/моль совершает замкнутый процесс (рис.). Температура в точках 1 и 2 равна: T1 = 300 К; Т2 = 496 К. Найти работу газа за цикл. [ A = 1162 Дж ]
32.5. Давление ν молей идеального газа связано с температурой по закону: Т = αp 2 (α = const). Найти работу газа при увеличении объема от значения V1 до значения V2. Выделяется или поглощается при этом тепло? [смотрите ответ в общем файле темы]
32.6. В цилиндре под невесомым поршнем находится газ. Поршень связан с дном цилиндра пружиной. Газ расширяется из состояния с параметрами p1, V1 в состояние p2, V2. Определить работу газа. [смотрите ответ в общем файле темы]
32.7. ν молей идеального газа помещены в герметическую упругую оболочку. Упругость оболочки такова, что квадрат объема пропорционален температуре. На сколько изменится энергия оболочки, если газ нагреть от температуры T1 до температуры T2? Какова теплоемкость системы? Теплоемкостью оболочки и внешним давлением пренебречь. [смотрите ответ в общем файле темы]
32.8. При изотермическом процессе газ совершил работу 1000 Дж. На сколько увеличится внутренняя энергия этого газа, если ему сообщить количество теплоты вдвое больше, чем в первом случае, а процесс проводить изохорически? [2000 Дж]
32.9. Найти количество теплоты, сообщенное газу в процессе 1 – 2 (рис.). [ Q = 3pV/4 ]
32.10. Один моль идеального газа совершает процесс 1 – 2 – 3 (рис.). Известны: давление p1, p2 и объем V1, V2. Найти поглощенное газом в этом процессе количество теплоты. [смотрите ответ в общем файле темы]
32.11. Один моль идеального газа нагревают сначала изотермически. При этом он совершает работу 10 Дж. Затем его нагревают изобарически, сообщая ему то же количество теплоты. Какую работу совершает газ во втором случае? [4 Дж]
32.12. Водород массой m = 1 кг при начальной температуре T1 = 300 K охлаждают изохорически так, что его давление падает в η = 3 раза. Затем газ расширяют при постоянном давлении до начальной температуры. Найти произведенную газом работу. [ A = 8.3×10 5 Дж ]
32.13. Один моль идеального газа переводят из начального состояния 1 в конечное 4 в процессе, представленном на рис. Какое количество теплоты подвели к газу, если ΔT = Т4 − T1 = 100 K? [ Q = 415 Дж ]
32.14. В вертикальном цилиндре под тяжелым поршнем находится газ при температуре T. Масса поршня m, его площадь S, объем газа V. Для повышения температуры газа на ΔT ему сообщили количество теплоты Q. Найдите изменение внутренней энергии газа. Атмосферное давление po, трения нет. [смотрите ответ в общем файле темы]
32.15. Для нагревания некоторого количества газа с молярной массой M = 28 г/моль на ΔT = 14 K при p = const требуется количество теплоты Q = 10 Дж. Чтобы охладить его на ту же ΔT при V = const требуется отнять Q = 8 Дж. Определить массу газа. [ m ≅ 0.48 г ]
32.16. В вертикальном цилиндре на высоте h от дна находится поршень. Под поршнем — идеальный газ. На поршень положили гирю массой m. После установления теплового равновесия с окружающей средой цилиндр теплоизолировали и газ начали нагревать. Какое количество теплоты следует подвести к газу, чтобы поршень вернулся в исходное положение. Трения нет. [ Q = 5mgh/2 ]
32.17. В вертикальном цилиндре под невесомым поршнем находится гелий. Объем гелия Vo, а давление 3po (po – атмосферное давление). Поршень удерживается сверху упорами (рис.). Какое количество теплоты необходимо отнять у гелия чтобы его объем стал Vo/2. Трения нет. [ Q = 17poVo/4 ]
32.19. Теплоизолированный сосуд объемом V = 22,4 л разделен пополам теплопроводящей перегородкой. В первую половину сосуда вводят m1 = 11,2 г азота при температуре t1 = 20 °С, а во вторую – m2 = 16,8 г азота при t2 = 15 °С. Какое давление установится в первой половине после выравнивания температур? Система теплоизолирована. [ p ≅ 86 кПа ]
32.20. Баллон емкостью V1 содержащий ν1 молей газа при температуре T1, соединяют с баллоном емкостью V2, содержащим ν2 молей того же газа при температуре T2. Какие установятся давление и температура. Система теплоизолирована. [смотрите ответ в общем файле темы]
32.21. Над одним молем идеального газа совершается процесс из двух изохор и двух изобар (рис.). Температуры в точках 1 и 3 равны T1 и T3. Определить работу газа за цикл, если точки 2 и 4 лежат на одной изотерме. [смотрите ответ в общем файле темы]
32.22. Моль идеального газа совершает цикл из двух изохор и двух изобар (рис.). Работа газа за цикл A = 200 Дж. Максимальная и минимальная температуры в цикле отличаются на ΔT = 60 К. Отношение давлений на изобарах равно 2. Найти отношение объемов на изохорах. [ ≅ 3 ]
32.23. Внутри цилиндрического сосуда под поршнем массы m находится идеальный газ под давлением p. Площадь поршня S, внешнего давления нет. Вначале поршень удерживается на расстоянии h1 от дна сосуда (рис.). Поршень отпустили. После прекращения колебаний поршень остановился. На каком расстоянии от дна он остановился? Трения нет. Тепловыми потерями и теплоемкостью поршня и цилиндра пренебречь. [смотрите ответ в общем файле темы]
32.24. В гладкой трубке между двумя поршнями массой m находится один моль идеального газа. В начальный момент скорости поршней направлены в одну сторону и равны v и 3v (рис.), а температура газа To. Найти максимальную температуру газа. Внешнего давления и трения нет. [смотрите ответ в общем файле темы]
32.25. В горизонтальном неподвижном цилиндре, закрытом поршнем массы m, находится один моль идеального газа. Газ нагревают. При этом поршень, двигаясь равномерно, приобретает скорость v. Найдите количество теплоты, сообщенное газу. Теплоемкостью сосуда и поршня, а также внешним давлением пренебречь. [ Q = 5mv 2 /4 ]
32.26. Сосуд, содержащий некоторое количество азота, движется со скоростью v = 100 м/с. На сколько изменится температура азота, если сосуд внезапно остановить? [ ΔT = Mv 2 /(5R) ]
32.27. В гладкой горизонтальной трубе находятся два поршня массами m и 3m. Между поршнями идеальный газ при давлении po. Объем между поршнями Vo (рис.). Первоначально поршни неподвижны, затем их отпускают. Найти максимальные скорости поршней. Труба длинная, внешнего давления нет. [смотрите ответ в общем файле темы]
32.28. Один моль идеального газа изобарически нагрели на ΔT = 72 K, сообщив ему количество теплоты Q = 1,6 кДж. Найти величину γ = cp/cV. [ γ = 1.6 ]
32.29. Вычислить γ = cp/cV для газовой смеси, состоящей из ν1 = 2 молей кислорода и ν2 = 3 молей углекислого газа. [ γ ≅ 1,6]
32.30. Теплоизолированный небольшой сосуд откачан до глубокого вакуума. Окружающая сосуд атмосфера состоит из идеального одноатомного газа при температуре 300 К. В сосуде открывается небольшое отверстие и он заполняется газом. Какую температуру будет иметь газ в сосуде сразу после заполнения? [500 K]
32.31. Определить скорость истечения гелия из теплоизолированного сосуда в вакуум через малое отверстие. Температура газа в сосуде T = 1000 K, скоростью газа в сосуде пренебречь. [ v ≅ 3.3×10 3 м/с]
32.32. Горизонтальный цилиндрический сосуд разделен подвижным поршнем. Справа от поршня одноатомный идеальный газ с параметрами: po; Vo; To, слева – вакуум (рис.). Поршень соединен с левым торцом цилиндра пружиной, собственная длина которой равна длине сосуда. Определить теплоемкость системы в этом состоянии. Теплоемкостью поршня и цилиндра пренебречь. Трения нет. [ C = 2poVo/To ]
32.33. Над идеальным двухатомным газом совершают процесс p = αV (α = const). Какова молярная теплоемкость газа в этом процессе? [c = 3R]
32.34. С одним молем идеального одноатомного газа проводят процесс: p = po — αV, где α – известная константа. Определить, при каких значениях объема газ получает тепло, а при каких отдает. Объем в процессе возрастает.
32.35. В процессе расширения азота его объем увеличился на 2 %, а давление уменьшилось на 1 %. Какая часть теплоты, полученной азотом, была превращена в работу? Удельная теплоемкость азота при постоянном объеме cV = 745 Дж/(кг • К). [ ≅ 0.44 ]
32.36. В цилиндрическом горизонтальном сосуде находится гладкий подвижный поршень. Слева и справа от поршня находится по одному молю идеального одноатомного газа. Температура газа в левой части поддерживается постоянной, а газ в правой части нагревается. Найдите теплоемкость газа в правой части в момент, когда поршень делит сосуд пополам. [C = 2R]
32.37. В вертикальном цилиндре под поршнем площадью S и массой m находится 1 моль идеального одноатомного газа. Под поршнем включается нагреватель, мощность которого N. Определите установившуюся скорость движения поршня. Атмосферное давление po, газ теплоизолирован, трения нет. [смотрите ответ в общем файле темы]
32.38. Мыльный пузырь содержит ν молей идеального одноатомного газа. Определить теплоемкость этой системы. Атмосферное давление не учитывать. [ C = 3νR ]
32.39. По трубе, в которой работает электрический нагреватель, пропускают газ (рис.). Определить мощность нагревателя, если разность температур газа на выходе и на входе равна ΔТ = 5 К, а массовый расход газа μ = 720 кг/ч. Молярная теплоемкость газа при постоянном давлении cp = 29,3 Дж/(моль • К), его молярная масса M = 29 г/моль. [ N ≅ 1.01 кВт ]
32.40. Из небольшого отверстия в баллоне с сжатым гелием вытекает струя гелия со скоростью v. Найдите разность температур гелия в баллоне и в струе. Давление в струе считать равным внешнему давлению, скоростью газа в баллоне пренебречь. [ ΔT = Mv 2 /(5R) ]
32.41. Одинаковые сообщающиеся сосуды закрыты поршнями массой m = 5 кг и M = 10 кг и соединены тонкой трубкой с краном (рис.). Под поршнями идеальный одноатомный одинаковый газ. Сначала кран закрыт, поршень M находится на высоте H = 10 см от дна, а температура одинакова. На какую высоту передвинется поршень m после открытия крана? Система теплоизолирована, атмосферного давления нет. [ 20 см ]
32.42. В горизонтальной открытой трубе сечением S без трения могут двигаться два поршня массами m и M. Начальное расстояние между поршнями l, атмосферное давление po. При закрепленных поршнях воздух между ними откачали, затем поршни отпустили. Какое количество теплоты выделится в результате их абсолютно неупругого столкновения? [ Q = poSl ]
32.43. Один моль идеального газа совершает цикл 1 – 2 – 3 – 1, состоящий из изохоры 1 – 2 и двух процессов, представляемых отрезками прямых в координатах p – V (рис.). Определить работу газа за цикл, если известны: температура T1, Т2 = 4Т1, а также Т2 = Т3. Линия 3 – 1 проходит через начало координат. [ A = 3RT1/2 ]
Термодинамика и молекулярная физика
1. При температуре 250 K и давлении плотность газа равна Какова молярная масса этого газа? Ответ приведите в кг/моль с точностью до десятитысячных.
2. Воздух охлаждали в сосуде постоянного объема. При этом температура воздуха в сосуде снизилась в 4 раза, а его давление уменьшилось в 2 раза. Оказалось, что кран у сосуда был закрыт плохо, и через него просачивался воздух. Во сколько раз увеличилась масса воздуха в сосуде?
3. Температура нагревателя идеального теплового двигателя Карно 227 °C, а температура холодильника 27 °C. Рабочее тело двигателя совершает за цикл работу, равную 10 кДж. Какое количество теплоты получает рабочее тело от нагревателя за один цикл? Ответ приведите в килоджоулях.
4. Из стеклянного сосуда стали выпускать сжатый воздух, одновременно охлаждая сосуд. При этом температура воздуха упала вдвое, а его давление уменьшилось в 3 раза. Масса воздуха в сосуде уменьшилась в k раз. Найдите k.
5. Температура нагревателя идеального теплового двигателя Карно равна а температура холодильника равна Рабочее тело получает от нагревателя за один цикл количество теплоты 25 кДж. Какую работу совершает за цикл рабочее тело двигателя? Ответ укажите в килоджоулях с точностью до десятых.
6. Одноатомный идеальный газ в количестве молей поглощает количество теплоты 2 кДж. При этом температура газа повышается на 20 К. Работа, совершаемая газом в этом процессе, равна 1 кДж. Чему, приблизительно, равно число молей газа? Ответ округлите до целого числа.
7. В термос с большим количеством льда при температуре заливают 0,5 кг воды с температурой При установлении теплового равновесия в сосуде расплавится лед массой Найдите ответ укажите в килограммах с точностью до сотых.
8. КПД тепловой машины 30%. За 10 с рабочему телу машины поступает от нагревателя 3 кДж теплоты. Чему равна средняя полезная мощность машины? Ответ приведите в ваттах.
9. Идеальная тепловая машина работает по циклу Карно, совершая за один цикл работу 2 кДж. Количество теплоты 2 кДж рабочее тело двигателя отдает за один цикл холодильнику, температура которого 17 °С. Чему равна температура нагревателя? Ответ приведите в градусах Цельсия.
10. Идеальная тепловая машина работает по циклу Карно, совершая за один цикл работу 2 кДж. Количество теплоты 6 кДж рабочее тело двигателя получает за один цикл от нагревателя, температура которого 217 °С. Чему равна температура холодильника? Ответ приведите в градусах Цельсия, округлите до целых.
11. Идеальная тепловая машина работает по циклу Карно, получая за один цикл от нагревателя 5 кДж теплоты и отдавая холодильнику З кДж теплоты. Температура холодильника 17 °С. Чему равна температура нагревателя? Ответ приведите в градусах Цельсия, округлите до целых.
12. Железному и алюминиевому цилиндрам сообщили одинаковое количество теплоты, что привело к одинаковым изменениям температуры цилиндров. Воспользовавшись таблицами, приведёнными в начале варианта, определите примерное отношение масс этих цилиндров Ответ округлите до целых.
13. В кубическом метре воздуха в помещении при температуре 20 °С находится водяных паров. Пользуясь таблицей плотности насыщенных паров воды, определите относительную влажность воздуха. Ответ приведите в процентах, округлите до целых.
| t, °С | |||||||
| 1,36 | 1,45 | 1,54 | 1,63 | 1,73 | 1,83 | 1,94 | 2,06 |
14. У теплового двигателя, работающего по циклу Карно, температура нагревателя 500 К, а температура холодильника 300 К. Рабочее тело за один цикл получает от нагревателя количество теплоты, равное 40 кДж. Какую работу совершает за цикл рабочее тело двигателя? Ответ укажите в килоджоулях.
15. Два моля идеального газа находились в баллоне, где имеется клапан, выпускающий газ при давлении внутри баллона более При температуре 300 К давление в баллоне было равно Затем газ нагрели до температуры 600 К. Сколько газа при этом вышло из баллона? Ответ приведите в молях, округлите до десятых.
16. В кастрюлю с 2 л воды температурой 25 °С долили 3 л кипятка температурой 100 °С. Какова будет температура воды после установления теплового равновесия? Теплообмен с окружающей средой и теплоемкость кастрюли не учитывайте. Ответ приведите в градусах цельсия.
17. В теплоизолированный сосуд с большим количеством льда при температуре заливают воды с температурой Какая масса льда расплавится при установлении теплового равновесия в сосуде? Ответ приведите в килограммах.
18. В калориметр с водой бросают кусочки тающего льда. В некоторый момент кусочки льда перестают таять. К концу процесса масса воды увеличилась на 84 г. Какова начальная масса воды, если ее первоначальная температура 20 °С? Ответ приведите в килограммах.
19. В теплоизолированный сосуд с большим количеством льда при температуре заливают теплой воды. Какова была начальная температура воды, если при установлении теплового равновесия в сосуде расплавилось 560 г льда? Ответ приведите в градусах цельсия.
20. Идеальный газ изохорно нагревают так, что его температура изменяется на а давление — в 1,6 раза. Масса газа постоянна. Какова начальная температура газа по шкале Кельвина?
21. Идеальный газ изобарно нагревают так, что его температура изменяется на а объём — в 1,4 раза. Масса газа постоянна. Какова начальная температура газа по шкале Кельвина?
23. Для определения удельной теплоемкости вещества тело массой 450 г, нагретое до температуры 100 °С, опустили в калориметр, содержащий 200 г воды. Начальная температура калориметра с водой 23 °С. После установления теплового равновесия температура тела и воды стала равна 30 °С. Определите удельную теплоемкость вещества исследуемого тела. Теплоемкостью калориметра пренебречь. Ответ приведите в Дж/(кг · К) и округлите до целого.
24. На графике приведена зависимость КПД идеальной тепловой машины от температуры ее холодильника. Чему равна температура нагревателя этой тепловой машины? Ответ приведите в Кельвинах.
25. На графике приведена зависимость КПД идеальной тепловой машины от температуры её холодильника. Чему равна температура нагревателя этой тепловой машины? Ответ приведите в кельвинах.
26. На рисунке приведен график зависимости внутренней энергии порции идеального газа от температуры Газ нагревают при постоянном объеме. Чему равна теплоемкость этой порции данного газа в рассматриваемом процессе? Ответ приведите в Дж/К.
27. В закрытом цилиндрическом сосуде находится влажный воздух при температуре 100 °С. Для того, чтобы на стенках этого сосуда выпала роса, требуется изотермически изменить объем сосуда в 25 раз. Чему приблизительно равна первоначальная абсолютная влажность воздуха в сосуде? Ответ приведите в г/м3, округлите до целых.
28. Кусок льда, имеющий температуру 0 °С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 10 °С, требуется количество теплоты 200 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 120 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь. Ответ приведите в градусах Цельсия.
1) вода при температуре выше 0 °С 2) вода при температуре 0 °С
3) лёд при температуре 0 °С 4) смесь воды и льда при температуре 0 °С
30. Идеальный одноатомный газ изобарно расширили от объёма 1 л до объёма 3 л, затем изохорно охладили так, что его давление уменьшилось от 2 105 Па до 105 Па, после чего газ вернули в исходное состояние так, что его давление линейно возрастало при уменьшении объёма. Какую работу совершил газ в этом процессе? Ответ приведите в джоулях.
31. Идеальный одноатомный газ изобарно сжали от объёма 3 л до объёма 1 л, затем изохорно нагрели так, что его давление увеличилось от 105 Па до 2 105 Па, после чего газ вернули в исходное состояние так, что его давление линейно убывало при увеличении объёма. Какую работу совершил газ в этом процессе? Ответ приведите в джоулях.
32. Идеальная тепловая машина с температурой холодильника 300 К и температурой нагревателя 400 К за один цикл своей работы получает от нагревателя количество теплоты 10 Дж. За счёт совершаемой машиной работы груз массой 10 кг поднимается вверх с поверхности земли. На какую высоту над землёй поднимется этот груз через 100 циклов работы машины? Ответ приведите в метрах.
33. Идеальная тепловая машина с температурой холодильника 300 К и температурой нагревателя 500 К за один цикл своей работы получает от нагревателя количество теплоты 8 Дж. За счёт совершаемой машиной работы груз массой 16 кг втаскивается вверх по гладкой наклонной плоскости, стоящей на земле. На какую высоту над уровнем земли поднимется этот груз через 100 циклов работы машины? Ответ приведите в метрах.
34. Поршень может свободно без трения перемещаться вдоль стенок горизонтального цилиндрического сосуда. В объёме, ограниченном дном сосуда и поршнем, находится воздух (см. рисунок). Площадь поперечного сечения сосуда равна 25 см2, расстояние от дна сосуда до поршня равно 20 см, атмосферное давление 100 кПа, давление воздуха в сосуде равно атмосферному. Поршень медленно перемещают на 5 см вправо, при этом температура воздуха не меняется. Какую силу требуется приложить, чтобы удержать поршень в таком положении? Ответ приведите в ньютонах.
35. С идеальным газом происходит циклический процесс, диаграмма p–V которого представлена на рисунке. Наинизшая температура, достигаемая газом в этом процессе, составляет 300 К. Определите количество вещества этого газа. Ответ укажите в молях с точностью до двух знаков после запятой.
36. С идеальным газом в количестве 0,24 моля происходит циклический процесс, VT-диаграмма которого представлена на рисунке. Определите наименьшее давление газа в этом процессе. Ответ укажите в килопаскалях, округлите до целых.
37. С идеальным газом происходит циклический процесс, pT–диаграмма которого представлена на рисунке. Наименьший объём, который занимает газ в этом процессе, составляет 6 л. Определите количество вещества этого газа. Ответ укажите в молях с точностью до сотых.
38. Во время опыта абсолютная температура воздуха в сосуде под поршнем повысилась в 2 раза, и он перешёл из состояния 1 в состояние 2 (см. рисунок). Поршень прилегал к стенкам сосуда неплотно, и сквозь зазор между ним мог просачиваться воздух. Рассчитайте отношение числа молекул газа в сосуде в конце и начале опыта. Воздух считать идеальным газом.
39. Во время опыта абсолютная температура воздуха в сосуде понизилась в 2 раза, и он перешёл из состояния 1 в состояние 2 (см. рисунок). Кран у сосуда был закрыт неплотно, и сквозь него мог просачиваться воздух. Рассчитайте отношение числа молекул газа в сосуде в конце и начале опыта. (Ответ округлить до десятых.) Воздух считать идеальным газом.
40. В стакан калориметра налили 150 г воды. Начальная температура калориметра и воды 55 °С. В эту воду опустили кусок льда, имевшего температуру 0 °С. После того как наступило тепловое равновесие, температура воды в калориметре стала 5 °С. Определите массу льда. Теплоёмкостью калориметра пренебречь. Удельную теплоту плавления льда принять равной 3,3·105 Дж/кг. Ответ приведите в граммах и округлите до целого числа.
41. Тело массой 800 г, нагретое до температуры 100 °С, опустили в калориметр, содержащий 200 г воды. Начальная температура калориметра и воды равна 30 °С. После установления теплового равновесия температура тела и воды в калориметре 37 °С. Определите удельную теплоёмкость вещества исследуемого тела. Теплоёмкостью калориметра пренебречь. Ответ приведите в Дж/(кг · °С), округлите до целых.
42. При проведении эксперимента по измерению удельной теплоёмкости вещества металлический цилиндр массой 0,15 кг был вынут из кипящей воды и опущен в воду, имеющую температуру 20 °С. Масса холодной воды 0,1 кг. После установления теплового равновесия температура металла и воды стала равной 30 °С. Чему равна удельная теплоёмкость вещества, из которого сделан цилиндр? Теплоёмкостью калориметра пренебречь. Ответ приведите в Дж/(кг · °С).
43. На рисунке показан график изотермического сжатия газа при температуре 150 К. Какое количество газообразного вещества содержится в этом сосуде? Ответ приведите в молях, округлив до целого.
44. Для определения удельной теплоёмкости вещества тело массой 400 г, нагретое до температуры 100 °С, опустили в калориметр, содержащий 200 г воды. Начальная температура калориметра и воды 23 °С. После установления теплового равновесия температура тела и воды стала равной 30 °С. Определите удельную теплоёмкость вещества исследуемого тела. Теплоёмкостью калориметра пренебречь. Ответ приведите в Дж/(кг · С°).
45. На рисунке показан график изменения давления 32 моль газа при изохорном нагревании. Каков объём этого газа? Ответ приведите в м3 с точностью до десятых.
46. Во время опыта абсолютная температура воздуха в сосуде понизилась в 2 раза, и он перешёл из состояния 1 в состояние 2 (см. рисунок). Кран у сосуда был закрыт неплотно, и сквозь него мог просачиваться воздух. Рассчитайте отношение количества молекул газа в сосуде в конце и начале опыта. Воздух считать идеальным газом. (Ответ округлить до сотых.)
47. Вертикальный цилиндр закрыт горизонтально расположенным поршнем массой 1 кг и площадью 0,02 м2, который может свободно перемещаться. Под поршнем находится 0,1 моля идеального одноатомного газа при некоторой температуре Над поршнем находится воздух при нормальном атмосферном давлении. Сначала газу сообщили количество теплоты 3 Дж, потом закрепили поршень и охладили газ до начальной температуры При этом давление газа под поршнем стало равно атмосферному. Чему равна температура ? Ответ укажите в кельвинах с точностью до десяток.
48. Вертикальный цилиндр закрыт горизонтально расположенным поршнем массой 1 кг и площадью 0,02 м2, который может свободно перемещаться. Под поршнем находится 0,1 моль идеального одноатомного газа при некоторой температуре T0. Над поршнем находится воздух при нормальном атмосферном давлении. Сначала от газа отняли количество теплоты 100 Дж. Потом закрепили поршень и нагрели газ до начальной температуры T0. При этом давление газа под поршнем стало в 1,2 раза больше атмосферного. Чему равна температура T0? Ответ укажите в Кельвинах с точностью до целых.
49. В теплоизолированном сосуде под поршнем находится 1 моль гелия при температуре 450 К (обозначим это состояние системы номером 1). В сосуд через специальный патрубок с краном добавили еще 2 моля гелия при температуре 300 К, и дождались установления теплового равновесия. После этого, убрав теплоизоляцию, весь оказавшийся под поршнем газ медленно изобарически расширили, изменив его объём в 2 раза (обозначим это состояние системы номером 2). Во сколько раз увеличилась внутренняя энергия системы при переходе из состояния 1 в состояние 2? (Ответ округлить до десятых.)
50. Чему равна работа, совершаемая идеальным одноатомным газом при реализации процесса 1–2–3 (см. рисунок)? Ответ укажите в джоулях с точностью до десятых.
51. Чему равна работа, совершаемая идеальным одноатомным газом при реализации процесса 1–2–3 (см. рисунок). Ответ укажите в джоулях с точностью до десятых.
52. В закрытом сосуде находится 2 г водяного пара под давлением 50 кПа и при температуре 100 ºС. Не изменяя температуры, объём сосуда уменьшили в 4 раза. Найдите массу образовавшейся при этом воды. Ответ приведите в граммах.
53. В закрытом сосуде находится 6 г водяного пара под давлением 25 кПа и при температуре 100 °С. Не изменяя температуры, объём сосуда уменьшили в 8 раз. Найдите массу пара, оставшегося после этого в сосуде. Ответ приведите в граммах.
54. В сосуде под поршнем при температуре 100 ºС находится 2 г водяного пара и такое же количество воды. Не изменяя температуры, объём сосуда увеличили в 3 раза. Определите массу воды, перешедшей при этом в пар. Ответ приведите в граммах.
55. В сосуде под поршнем при температуре 100 °С находится 2 г водяного пара и такое же количество воды. Не изменяя температуры, объём сосуда увеличили в 3 раза. Определите массу пара в сосуде после изменения объёма. Ответ приведите в граммах.
56. В атмосферном воздухе содержатся кислород и азот. Среднеквадратичная скорость молекул кислорода равна 468 м/с. Чему равна среднеквадратичная скорость молекул азота? Ответ укажите в м/с с точностью до целых.
57. В атмосферном воздухе содержатся кислород и аргон. Среднеквадратичная скорость молекул кислорода равна 470 м/с. Чему равна среднеквадратичная скорость молекул аргона? Ответ укажите в м/с с точностью до целых.
Читайте также:

