Лямбда в статистике обозначает

Обновлено: 04.02.2025

Лямбда-исчисление (также пишется как λ-исчисление) это формальная система в математическая логика для выражения вычисление на основе функции абстракция и заявление используя переменную привязка и замена. Это универсальный модель вычисления который можно использовать для моделирования любого Машина Тьюринга. Его ввел математик Церковь Алонсо в 1930-х годах в рамках его исследования основы математики.

Лямбда-исчисление состоит из построения лямбда-членов и выполнения над ними операций редукции. В простейшей форме лямбда-исчисления термины строятся с использованием только следующих правил:

Синтаксис	Имя	Описание
Икс	Переменная	Символ или строка, представляющая параметр или математическое / логическое значение.
(λИкс.M)	Абстракция	Определение функции (M является лямбда-термином). Переменная Икс становится граница в выражении.
(M N)	Заявление	Применение функции к аргументу. M и N - лямбда-термины.

производя такие выражения, как: (λИкс.λу. (λz. (λИкс.z x) (λу.z y)) (х у)). Скобки можно опустить, если выражение однозначно. Для некоторых приложений могут быть включены термины для логических и математических констант и операций.

Операции восстановления включают:

Операция	Имя	Описание
(λИкс.M[Икс]) → (λу.M[у])	α-преобразование	Переименование связанных переменных в выражении. Используется, чтобы избежать коллизии имен.
((λИкс.M) E) → (M[Икс := E])	β-редукция	Замена связанных переменных выражением аргумента в теле абстракции.

Если Индексирование де Брёйна используется, то α-преобразование больше не требуется, так как не будет конфликтов имен. Если повторное применение этапов редукции в конечном итоге завершается, то к Теорема Черча – Россера это произведет β-нормальная форма.

Имена переменных не нужны, если используется универсальная лямбда-функция, например Йота и Джот, который может создавать любое поведение функции, вызывая ее в различных комбинациях.

Содержание

Объяснение и приложения

Лямбда-исчисление Тьюринг завершен, то есть это универсальный модель вычисления который можно использовать для моделирования любого Машина Тьюринга. [1] Его тезка, греческая буква лямбда (λ), используется в лямбда-выражения и лямбда-термины обозначать привязка переменная в функция.

Лямбда-исчисление может быть нетипизированный или же напечатанный. В типизированном лямбда-исчислении функции могут применяться только в том случае, если они способны принимать заданный "тип" входных данных. Типизированные лямбда-исчисления слабее чем нетипизированное лямбда-исчисление, которое является основной темой этой статьи, в том смысле, что типизированные лямбда-исчисления могут выразить меньше чем нетипизированное исчисление, но, с другой стороны, типизированные лямбда-исчисления позволяют доказать больше вещей; в просто типизированное лямбда-исчисление это, например, теорема, согласно которой каждая стратегия оценки завершается для каждого просто типизированного лямбда-члена, тогда как оценка нетипизированных лямбда-членов не должна завершаться. Одной из причин, по которой существует множество различных типизированных лямбда-исчислений, было желание сделать больше (того, что может делать нетипизированное исчисление), не отказываясь от возможности доказать сильные теоремы об исчислении.

Лямбда-исчисление имеет приложения во многих различных областях в математика, философия, [2] лингвистика, [3] [4] и Информатика. [5] Лямбда-исчисление сыграло важную роль в развитии теории теория языков программирования. Функциональные языки программирования реализовать лямбда-исчисление. Лямбда-исчисление также является актуальной темой исследований в Теория категорий. [6]

История

Лямбда-исчисление было введено математиком Церковь Алонсо в 1930-х годах в рамках расследования основы математики. [7] [а] Было показано, что исходная система логически непоследовательный в 1935 году, когда Стивен Клини и Дж. Б. Россер разработал Парадокс Клини – Россера. [8] [9]

Впоследствии, в 1936 году, Черч выделил и опубликовал только ту часть, которая имеет отношение к вычислениям, то, что сейчас называется нетипизированным лямбда-исчислением. [10] В 1940 году он также представил более слабую в вычислительном отношении, но логически последовательную систему, известную как просто типизированное лямбда-исчисление. [11]

До 1960-х годов, когда было выяснено его отношение к языкам программирования, лямбда-исчисление было всего лишь формализмом. Благодаря Ричард Монтегю и других приложений лингвистов в семантике естественного языка, лямбда-исчисление начало занимать почетное место в обеих лингвистике. [12] и информатика. [13]

Происхождение символа лямбда

По поводу того, почему Черч использует греческую букву, существует некоторое противоречие. лямбда (λ) как обозначение функции-абстракции в лямбда-исчислении, возможно, частично из-за противоречивых объяснений самого Черча. По словам Кардоне и Хиндли (2006):

Дана Скотт также обращался к этому противоречию в различных публичных лекциях. [14] Скотт вспоминает, что однажды он задал вопрос о происхождении лямбда-символа зятю Черча Джону Аддисону, который затем написал своему тестю открытку:

Уважаемый профессор Черч,
Рассел имел оператор йоты, Гильберт обладал эпсилон-оператор. Почему вы выбрали лямбду для своего оператора?

По словам Скотта, весь ответ Черча состоял в том, чтобы вернуть открытку со следующей аннотацией: "Ини, Мини, Мини, Мо".

Неформальное описание

Мотивация

можно переписать на анонимная форма в качестве

(читается как "кортеж Икс и у является нанесенный на карту к Икс 2 + у 2 + y ^ > "). По аналогии,

можно переписать в анонимной форме как

где ввод просто сопоставляется сам с собой.

может быть переработан в

Этот метод, известный как карри, преобразует функцию, которая принимает несколько аргументов, в цепочку функций, каждая из которых имеет один аргумент.

тогда как оценка каррированной версии требует еще одного шага

чтобы достичь того же результата.

Лямбда-исчисление

Лямбда-исчисление состоит из языка лямбда-термины, который определяется определенным формальным синтаксисом и набором правил преобразования, которые позволяют манипулировать лямбда-терминами. Эти правила преобразования можно рассматривать как эквациональная теория или как Рабочее определение.

Как описано выше, все функции в лямбда-исчислении являются анонимными функциями, не имеющими имен. Они принимают только одну входную переменную с карри используется для реализации функций с несколькими переменными.

Лямбда-термины

Следующие три правила дают индуктивное определение который может применяться для построения всех синтаксически правильных лямбда-терминов:

Ничто иное не является лямбда-термином. Таким образом, лямбда-член действителен тогда и только тогда, когда его можно получить повторным применением этих трех правил. Однако некоторые скобки можно опустить по определенным правилам. Например, крайние круглые скобки обычно не пишутся. Видеть Обозначение, ниже.

Функции, которые работают с функциями

В лямбда-исчислении функции считаютсяпервоклассные ценности', поэтому функции могут использоваться как входы или возвращаться как выходы из других функций.

Альфа-эквивалентность

Для определения β-редукции необходимы следующие определения:

Бесплатные переменные

В свободные переменные терма - это переменные, не связанные абстракцией. Набор свободных переменных выражения определяется индуктивно:

Замены с избеганием захвата

β-редукция

Лямбда-исчисление можно рассматривать как идеализированную версию функционального языка программирования, например Haskell или же Стандартный ML.С этой точки зрения β-редукция соответствует шагу вычислений. Этот шаг можно повторять путем дополнительных β-редукций до тех пор, пока не останется больше приложений для уменьшения. В нетипизированном лямбда-исчислении, представленном здесь, этот процесс редукции не может завершаться. Например, рассмотрим термин Ω = ( λ Икс . Икс Икс ) ( λ Икс . Икс Икс ) .Здесь ( λ Икс . Икс Икс ) ( λ Икс . Икс Икс ) → ( Икс Икс ) [ Икс := λ Икс . Икс Икс ] = ( Икс [ Икс := λ Икс . Икс Икс ] ) ( Икс [ Икс := λ Икс . Икс Икс ] ) = ( λ Икс . Икс Икс ) ( λ Икс . Икс Икс ) То есть термин сводится к самому себе за одно β-восстановление, и поэтому процесс восстановления никогда не закончится.

Другой аспект нетипизированного лямбда-исчисления заключается в том, что оно не делает различий между разными типами данных. Например, может быть желательно написать функцию, которая работает только с числами. Однако в нетипизированном лямбда-исчислении нет способа предотвратить применение функции к ценности истины, строки или другие нечисловые объекты.

Формальное определение

Определение

Лямбда-выражения состоят из:

переменные v₁, v₂, . ;
символы абстракции λ (лямбда) и. (точка);
скобки ().

Набор лямбда-выражений Λ может быть определяется индуктивно:

Если Икс переменная, то Икс ∈ Λ.
Если Икс переменная и M ∈ Λ, то (λИкс.M) ∈ Λ.
Если M, N ∈ Λ, то (M N) ∈ Λ.

Примеры правила 2 известны как абстракции и примеры правила 3 известны как Приложения. [15] [16]

Обозначение

Чтобы не перегружать нотацию лямбда-выражений, обычно применяются следующие соглашения:

Крайние круглые скобки опускаются: M N вместо (M N).
Предполагается, что приложения левоассоциативны: вместо ((M N) P) можно написать M N P. [17]
Тело абстракции расширяется как можно правее: λИкс.M N означает λИкс.(M N), а не (λИкс.M) N.
Сжимается последовательность абстракций: λИкс.λу.λz.N сокращенно λxyz.N. [18][17]

Свободные и связанные переменные

Говорят, что оператор абстракции λ связывает свою переменную везде, где она встречается в теле абстракции. Переменные, попадающие в область действия абстракции, называются граница. В выражении λИкс.M, часть λИкс часто называют связующее, как намек на то, что переменная Икс связывается добавлением λИкс к M. Все остальные переменные называются свободный. Например, в выражении λу.х х у, у является связанной переменной и Икс это свободная переменная. Также переменная привязана к ближайшей абстракции. В следующем примере единственное вхождение Икс в выражении связана второй лямбдой: λИкс.у (λИкс.z x).

Набор свободные переменные лямбда-выражения, M, обозначается FV (M) и определяется рекурсией по структуре терминов следующим образом:

Выражение, не содержащее свободных переменных, называется закрыто. Замкнутые лямбда-выражения также известны как комбинаторы и эквивалентны условиям в комбинаторная логика.

Снижение

Значение лямбда-выражений определяется тем, как выражения могут быть сокращены. [20]

Есть три вида сокращения:

α-преобразование: изменение связанных переменных;
β-редукция: применение функций к их аргументам;
η-редукция: который отражает понятие протяженности.

Мы также говорим о полученных эквивалентностях: два выражения α-эквивалент, если их можно α-преобразовать в одно и то же выражение. Аналогично определяются β-эквивалентность и η-эквивалентность.

Период, термин редекс, Короче для сводимое выражение, относится к подтерминам, которые могут быть сокращены одним из правил сокращения. Например, (λИкс.M) N является β-редексом в выражении замены N за Икс в M. Выражение, к которому сводится редекс, называется его сокращать; редукция (λИкс.M) N является M[Икс := N].

Если Икс не бесплатно в M, λИкс.M x также является η-редексом с редукцией M.

α-преобразование

α-преобразование, иногда известное как α-переименование, [21] позволяет изменять имена связанных переменных. Например, α-преобразование λИкс.Икс может дать λу.у. Термины, которые отличаются только α-преобразованием, называются α-эквивалент. Часто при использовании лямбда-исчисления α-эквивалентные термины считаются эквивалентными.

Точные правила α-преобразования не совсем тривиальны.Во-первых, при α-преобразовании абстракции переименовываются только вхождения переменных, которые связаны с той же абстракцией. Например, α-преобразование λИкс.λИкс.Икс может привести к λу.λИкс.Икс, но это могло нет приводит к λу.λИкс.у. Последний имеет значение, отличное от оригинала. Это аналогично понятию программирования переменное затенение.

Во-вторых, альфа-преобразование невозможно, если оно приведет к захвату переменной другой абстракцией. Например, если мы заменим Икс с у в λИкс.λу.Икс, получаем λу.λу.у, что совсем не одно и то же.

В языках программирования со статической областью видимости α-преобразование может использоваться для разрешение имени проще, гарантируя, что имя переменной маски имя в содержащем объем (видеть α-переименование для упрощения разрешения имен).

в Индекс Де Брёйна обозначение, любые два α-эквивалентных термина синтаксически идентичны.

Замена

Замена, письменная M[V := N], это процесс замены всех свободный появления переменной V в выражении M с выражением N. Подстановка терминов лямбда-исчисления определяется рекурсией по структуре терминов следующим образом (примечание: x и y являются только переменными, а M и N - любыми лямбда-выражениями):

Икс[Икс := N] = N у[Икс := N] = у, если Икс ≠ у (M₁ M₂)[Икс := N] = (M₁[Икс := N]) (M₂[Икс := N]) (λИкс.M)[Икс := N] = λИкс.M (λу.M)[Икс := N] = λу.(M[Икс := N]), если Икс ≠ у и у ∉ FV (N)

Для замены в абстракцию иногда необходимо α-преобразовать выражение. Например, это неверно для (λИкс.у)[у := Икс], чтобы получить λИкс.Икс, потому что замененный Икс должен был быть свободным, но оказался связанным. Правильная подстановка в этом случае - λz.Икс, с точностью до α-эквивалентности. Подстановка определяется однозначно с точностью до α-эквивалентности.

β-редукция

β-редукция отражает идею применения функции. β-редукция определяется в терминах замещения: β-редукция (λV.M) N является M[V := N].

Например, предполагая некоторую кодировку 2, 7, ×, мы имеем следующую β-редукцию: (λп.п × 2) 7 → 7 × 2.

β-редукцию можно рассматривать как то же самое, что и концепция локальная сводимость в естественный вычет, через Изоморфизм Карри – Ховарда.

η-редукция

η-редукция выражает идею протяженность, что в данном контексте состоит в том, что две функции одинаковы если и только если они дают одинаковый результат для всех аргументов. η-редукция преобразует λИкс.ж Икс и ж в любое время Икс не кажется свободным в ж.

η-редукция можно рассматривать как то же самое, что и концепция местная полнота в естественный вычет, через Изоморфизм Карри – Ховарда.

Нормальные формы и слияние

Для нетипизированного лямбда-исчисления β-редукция как правило переписывания ни то, ни другое сильно нормализующий ни слабо нормализующий.

Однако можно показать, что β-редукция сливаться при работе с α-преобразованием (т.е. мы считаем две нормальные формы равными, если возможно α-преобразование одной в другую).

Следовательно, как сильно нормализующие члены, так и слабо нормализующие члены имеют единственную нормальную форму. Для строго нормализующих членов любая стратегия редукции гарантированно приведет к нормальной форме, тогда как для слабо нормализующих членов некоторые стратегии редукции могут не найти ее.

Кодирование типов данных

Основное лямбда-исчисление можно использовать для моделирования логических значений, арифметика, структуры данных и рекурсия, как показано в следующих подразделах.

Арифметика в лямбда-исчислении

Есть несколько возможных способов определить натуральные числа в лямбда-исчислении, но наиболее распространенными являются Церковные цифры, который можно определить следующим образом:

и так далее. Или используя альтернативный синтаксис, представленный выше в Обозначение:

Изменяя то, что повторяется, и варьируя аргумент, к которому применяется эта повторяющаяся функция, можно достичь множества различных эффектов.

В задачах построения объяснительных моделей часто встает вопрос о нахождении критерия, по которому можно было бы классифицировать данные (построение дискриминирующей функции) и определить переменные, которые различают две или более возникающие совокупности (группы).

Например, некий исследователь в области образования может захотеть исследовать, какие переменные относят выпускника средней школы к одной из трех категорий: (1) поступающий в колледж, (2) поступающий в профессиональную школу или (3) отказывающийся от дальнейшего образования или профессиональной подготовки. Для этой цели исследователь может собрать данные о различных переменных, связанных с учащимися школы.

После выпуска большинство учащихся естественно должно попасть в одну из названных категорий.

Затем можно использовать Дискриминантный анализ для определения того, какие переменные дают наилучшее предсказание выбора учащимися дальнейшего пути.

Пусть имеется n наблюдений, разбитых на k групп (классов).

Каждое наблюдение характеризуется набором из m значений (независимые переменные). Также для каждого наблюдения известно, к какой из k групп оно принадлежит. Принадлежность объектов к разным классам выражается в том, что для объектов данного класса имеет распределение , j=1,…,k.

Задача состоит в том, чтобы для нового наблюдения определить группу (класс), к которой оно принадлежит.

Дискриминантный анализ предполагает, что являются m-мерными нормальными распределениями , j=1,…,k и имеющими плотности:

, j=1,…,k (1)

Здесь - m-мерный вектор средних значений, а - невырожденная ковариационная матрица ().

В таком случае, исходя из принципа максимального правдоподобия, будем считать областью притяжения закона множество таких наблюдений , где плотность распределения больше других. См. рис. 1.

В данном примере, где графики плотности пересекаются только в одной точке, получается, что вся прямая разбивается на 2 области притяжения.

Рис. 1. Области притяжения для k=2, m=1

Это равносильно тому, что линейно связанная с логарифмом плотности величина:

, j=1,…,k (2)

имеет наименьшее значение среди . Таким образом, n+1 наблюдение будет отнесено к i-группе, если (x)- имеет наименьшее значение.

Оценка качества дискриминации

Рассмотрим модель Фишера, которая является частным случаем нормальной дискриминантной модели при .

При k =2 нетрудно проверить, что поверхность, задаваемая условием , разделяет два класса уравнением:

Линейную функцию часто называют дискриминантной функцией, как функцию, описывающую гиперплоскость, по которой разделяются две группы. Мы же будем под дискриминантной функцией понимать линейную часть функции (x).

Обозначим через расстояние Махаланобиса между и . Чем более далекими в метрике Махаланобиса являются и , тем меньше вероятность ошибочной классификации.

В общем случае, . Расстояние Махаланобиса является мерой расстояния между двумя точками x и y в пространстве, определяемым двумя или более коррелированными переменными. Можно заметить, что в случае, когда переменные не коррелированны (), расстояние Махаланобиса совпадет с евклидовым.

При k>2 с помощью гиперплоскостей m–мерное пространство разбивается на k частей. В каждой из них содержится только одна точка из – та, к которой все точки данной части находятся ближе, чем к остальным в смысле расстояния Махаланобиса. См. рис. 2.

Рис. 2. Области притяжения для k=3, m=2

Для проверки гипотезы о равенстве средних в качестве статистик критерия используют статистики Уилкса (лямбда Уилкса):

Здесь T = – общая матрица рассеяния, матрица внутриклассового разброса: ,

где - матрица рассеяния j-го класса.

Очевидно, что ее значение меняется от 1.0 (нет дискриминации) до 0.0 (полная дискриминация).

Оказывается, что верно матричное тождество:

где R = – матрица разброса между элементами класса, – число элементов в j-м классе.

При выполнении гипотезы :

имеет распределение Фишера.

отклоняется (т.е. дискриминация значима), если

где - квантиль уровня .

Описание данных и постановка задачи

Имеется файл с данными boston.sta с ценами земельных участков в Бостоне. Всего в файле содержится 1012 участков (наблюдений).

Участок характеризуется 11 параметрами ORD1,…, ORD11 – непрерывные предикторы, а также одной группирующей категориальной переменной PRICE – характеризующий ценовой класс, к которому относиться данный участок (HIGH, MEDIUM, LOW). См. рис. 3.

Рис. 3. Таблица с исходными данными boston.sta

Цель: определить критерий, по которому можно классифицировать наблюдения по категории PRICE в зависимости от параметров участка (ORD1-ORD11), и, c его помощью, определить категорию PRICE для нового наблюдения.

Решение задачи по шагам

Для решения задачи перейдем на вкладку Анализ/Многомерный Разведочный анализ/Дискриминантный анализ. См. рис. 4.

В качестве группирующей переменной укажем переменную PRICE, в качестве независимых – переменные ORD1-ORD11. Анализ будем проводить пошагово. Количество шагов соответствует числу переменных.

Пошаговый анализ с включением/исключением на каждой итерации при помощи статистики Фишера определяет, стоит ли включать в модель соответствующую переменную.

Обычно в пошаговом анализе дискриминантной функции, переменные включают в модель, если соответствующее им значение F больше, чем значение F-включить, переменные удаляют из модели, если соответствующее им значение F меньше, чем значение F-исключить.

Заметим, что значение F-включить всегда должно быть больше, чем значение F-исключить. Если при проведении пошагового анализа с включением, вы пожелаете включить все переменные, установите в поле F-включить значение, равное очень маленькому числу (например, 0.0001), а в поле F-исключить значение 0.0.

Если при проведении пошагового анализа с исключением, вы пожелаете исключить все переменные из модели, установите в поле F-включить значение, равное очень большому числу (например, 0.9999), а в поле F-исключить чуть-чуть меньшее значение того же порядка (например, 0.9998).

Рис. 4. Пошаговый дискриминантный анализ

Нажмем кнопку ОК.

В следующем меню на вкладке Дополнительно установим опцию: Пошаговый с включением с F-вкл = 10 и вывод результатов на каждом шаге.

Нажмем кнопку ОК. См. рис. 5.

Рис. 5. Результаты анализа на 0-м шаге

Шаг 0.

Лямбда Уилкса равна 1 на 0-м шаге, т.к. никакой дискриминационной модели еще нет.

Нажмем кнопку Переменные вне модели. См. рис. 6.

Лямбда Уилкса. Значение посчитано по формуле (3) и определяет значение L, если бы соответствующая переменная была включена в модель на этом шаге.

Частная лямбда Уилкса. Эта статистика для одиночного вклада соответствующей переменной в дискриминацию между совокупностями является аналогом частной корреляции. Так как в модель еще не введено ни одной переменной, частная лямбда Уилкса равна лямбда Уилкса.

F-включить и p-значение. Считается также как и F-статистика для всей модели (формула (4)), только вместо лямбды Уилкса подставляется Частная лямбда Уилкса.

Взглянув на таблицу, вы видите, что наибольшие значения величины F-включить дает переменная ORD11 (последняя строка). Переменная с максимальным значением F-включить будет включена в модель на первом шаге (т.е. вносящая наибольший вклад в модель).

Рис. 6. Переменные вне модели на 0-м шаге

Шаг 1.

Анализ включил в модель переменную ORD11, т.к. она несет наибольший вклад среди прочих переменных в дискриминационную модель (наибольшее значение F-вкл). См. рис. 7.

Рис. 7. Результаты анализа на 1-м шаге

Нажав кнопку переменные в модели, получим следующую таблицу (рис. 8.)

Рис. 8. Переменные в модели на 1-м шаге

Далее, проводя аналогичные рассуждения, в модель будет включена переменная ORD4. См. рис. 9.

Рис. 9. Переменные в модели на 2-м шаге

Алгоритм дискриминантного анализа останавливается, если на очередном шаге F-вкл. в модель оказывается меньше заданного значения (в нашем примере F-вкл. = 10) или если на очередном шаге уже все переменные будут в модели.

В нашем случае анализ остановился на 7-м шаге (т.к. F (2, 1003) = 8,314937 < F-вкл. = 10 ). См. рис. 10.

Рис. 10. Итоги дискриминантного анализа

На вкладке Дополнительно можно вызвать пункт Итоги пошагового анализа (либо пункт Переменные в модели). См. рис. 11.

Рис. 11. Переменные, включенные модель к концу анализа

В итоге в модель было включено 7 переменных.

Кнопка Расстояние между группами выдаст таблицу с квадратами расстояний Махаланобиса между центрами групп. См. рис. 12.

Рис. 12. Квадраты расстояний Махаланобиса

Вместе с таблицей результатов расстояний Махаланобиса выводятся две другие таблицы результатов: одна с F-значениями, связанными с соответствующими расстояниями, а другая – с соответствующими p-уровнями. См. рис. 13.

Рис. 13. Значения F-статистики и p-уровней для расстояний Махаланобиса

Эти p-уровни должны интерпретироваться с осторожностью, если только в анализ не привносится сильная априорная гипотеза относительно того, какие пары групп должны показывать особенно большие (и значимые) расстояния.

Классификация

Перейдем к подменю Классификация. См. рис. 14.

Рис. 14. Подменю Классификация Дискриминантного анализа

Здесь, кроме уже описанных выше расстояний Махаланобиса (таблица с расстояниями на рис. 16), можно вывести коэффициенты функции классификации для каждой группы. См. рис. 15.

Рис. 15. Функции классификации (дискриминации)

На рис. 15 в каждом столбце находятся коэффициенты дискриминирующей функции для соответствующего класса (стоит еще раз отметить, что подразумевается линейная функция).

Рис. 16. Квадраты расстояния Махаланобиса до центров соответствующих групп

Также можно вывести матрицу классификации и классификацию наблюдений. См. рис. 17. и рис. 18.

Рис. 17. Матрица классификации

Обе таблицы основываются на результатах таблицы с квадратами расстояний Махаланобиса (см. выше).

Рис. 18. Классификация наблюдений

Стоит обратить внимание, что в предыдущих таблицах каждая группа была помечена априорной вероятностью (см. в названии переменных таблиц). Их можно задать на панели справа (См. рис. 14 и рис. 19).

Рис. 19. Априорные вероятности

Априорные вероятности отражают наши знания о природе явления перед проведением эксперимента.

Например, если мы знаем, что в начальных данных преобладают элитные земельные участки (PRICE = HIGH), то этот факт, конечно, должен повлиять на анализ, увеличивая долю наблюдений, помеченных в результате дискриминации как HIGH.

По умолчанию, в системе STATISTICA априорные вероятности задаются пропорционально размеру групп.

Вероятности, полученные после эксперимента, называются апостериорными. Они приведены в таблице на рис. 20.

Рис. 20. Апостериорные вероятности

Апостериорные вероятности связаны с априорными по следующей формуле:

где .

Литература

Рао С.Р. Линейные статистические методы и их применения, Наука 1968.

Розанов Ю.А. Теория вероятностей, случайные процессы и математическая статистика, Наука 1985.

Боровиков В.П. STATISTICA, искусство анализа данных на компьютере, Питер 2001.

Боровиков В.П. Нейронные сети. STATISTICA Neural Networks, Горячая линия – Телеком 2008.

Крамера и коэффициентом "лямбда". [c.552]

Мы рассмотрим статистики, обычно используемые для оценки статистической значимости и тесноты связи переменных, в таблице сопряженности. Статистическая значимость наблюдаемой связи обычно измеряется критерием Теснота связи важна с практической точки зрения. Обычно она имеет значение, если связь статистически значимая. Тесноту связи можно измерить коэффициентом корреляции фи, коэффициентом сопряженности Крамера и коэффициентом "лямбда". Эти статистики ниже описаны детальнее. [c.575]

Таким образом, связь не очень сильна. В этом случае V = о Так всегда происходит для таблицы Другой обычно рассчитываемой статистикой является коэффициент "лямбда". [c.578]

Мера в процентах улучшения прогнозирования значения зависимой переменной при данном значении независимой переменной. Значения коэффициента "лямбда" лежат в пределах от 0 до [c.578]

Значения коэффициента "лямбда" лежат в пределах от 0 до 1. Значение "лямбда", равное О, означает, что никакого улучшения в прогнозировании не наблюдается. Значение 1 указывает на то, что прогноз может быть сделан без ошибки. Это происходит тогда, когда каждая категория независимой переменной связана с одной категорией зависимой [c.579]

Симметричный коэффициент "лямбда" не дает предположения о какая из переменных зависимая. Он измеряет общее улучшение прогнозирования, когда прогноз уже сделан в обоих направлениях. [c.579]

Если нулевая гипотеза отклонена, то определите тесноту связи, используя статистики коэффициент сопряженности, Крамера, коэффициент "лямбда" или другие статистики). [c.580]

Л (лямбда) - коэффициент Оукена [c.830]

Коэффициент "лямбда" используется в том случае, когда переменные измерены с помощью номинальной шкалы, коэффициент (asymmetri lambda) показывает выраженное в процентах улучшение при прогнозировании значения зависимой переменной при данном значении независимой переменной, [c.578]

Асимметрический коэффициент "лямбда" подсчитывают для каждой из зависимых переменных. Также рассчитывают симметричный коэффициент (symmetri lambda) — средним значением двух асимметричных значений. [c.579]

Симметричный коэффициент "лямбда" не делает предположения о том, какая из переменных зависимая. Он измеряет прогнозирования, когда прогноз уже выполнен в обоих направлениях [14]. Значение асимметричного коэффициента "лямбда" в табл. 15.3, если в качестве переменной взять Internet, равно 0,333. Это указывает на то, что знание пола нашу возможность прогнозирования на 0,333, т.е. имеет место улучшение прогнозирования на 0,33%. Симметричный коэффициент "лямбда" также равен 0,33%. [c.579]

Часто, чтобы лучше уяснить суть связи переменных, вводят третью переменную. Статистика позволяет проверить статистическую значимость наблюдаемой в таблице, s o-i-i пряженности. С помощьюкоэффициента сопряженности, V -коэффициент Крамера и коэффициента "лямбда" определяют силу связи между переменными. [c.598]

Бессмысленно интерпретировать результаты анализа, если определенные дискрими-не являются статистически значимыми. Поэтому выполнить статистическую проверку нулевой гипотезы о равенстве средних всех функций во всех группах генеральной совокупности. В программе SPSS эта проверка базируется на коэффициенте лямбда (X) Уилкса. Если одновременно проверяют несколько [c.695]

Измерители линейной чувствительности к движению финансовых переменных используются под различными обозначениями. На рынке инструментов с фиксированным доходом чувствительность к движению процентных ставок измеряется дюрацией. На рынке акций чувствительность к фактору рынка в цепом (например, фондовому индексу) называется систематическим риском или коэффициентом бета. На рынке производных инструментов чувствительность

Коэффициент лямбда для апрельских 1992 г. опционов колл, для каждой из цен исполнения [c.121]

Лямбда (X) измеряет чувствительность цены опциона к изменениям волатильности цены акции и равна производной с по вола-тильности акций. Участники торгов, располагающие конфиденциальной информацией, способной влиять на рыночные курсы, стара- [c.126]

Классификация выручки. Самый простой способ оценки лямбды — это использование доли выручки фирмы, полученной в определенной стране, и сравнение ее с долей выручки средней фирмы в стране. [c.269]

Таким образом, фирма, которая получает лишь 40% своей выручки в Индонезии, в то время как средняя индонезийская фирма получает 80% выручки в своей стране, будет иметь лямбду, равную 0,5 для индонезийского суверенного риска. Тем не менее, заметим, что если оставшиеся 60% фирма получает в Таиланде, то нам следовало бы оце- [c.269]

Л (лямбда) - коэффициент Оукена [c.830]

В литературе помимо термина вега иногда используют термины каппа, лямбда, сигма, омега, зета. [c.221]

Крамера и коэффициентом "лямбда". [c.552]

Lambda — лямбда . Ожидаемая надбавка к прибыли (сверх безрисковой процентной ставки) на единицу чувствительности к некоторому стандартному фактору. Также чувствительность цены опциона к изменениям его неустойчивости. [c.980]

Измерение степени подверженности суверенному рисну (лямбда). В главе 7 представлены концепция подверженности суверенному риску и понятие лямбда как мера подверженности компании суверенному риску. В этом разделе мы бы хотели с интуитивной точки зрения обсудить, какие факторы определяют эту подверженность и как наилучшим образом оценить лямбду. Воздействие на компанию суверенного риска зависит почти от всех аспектов ее деятельности, начиная с того, где расположены ее фабрики и кто ее клиенты и заканчивая тем, в какой валюте заключаются контракты и насколько успешно фирма справляется с риском валютного обмена. Однако значительная часть этих данных относится к внутренней информации, которая недоступна при проведении оценки фирмы сторонними аналитиками. На практике, в таких случаях мы можем оценить лямбду, основываясь на одном из следующих подходов. [c.269]

Регрессия и государственные облигации. Второй подход к оценке лямбды связан с выведением регрессий доходности акций для каждой фирмы на формирующемся рынке — в сопоставлении с доходностью государственных облигаций, выпущенных данной страной. Например, в Бразилии это предполагало бы составление регрессии доходности по каждой бразильской акции в сопоставлении с доходностью бразильской государственной облигации. Наклон линии регрессии должен измерять, насколько чувствительна акция к изменениям в суверенном риске (поскольку доходы по государственным облигациям являются прямой мерой суверенного риска) и, таким образом, этот наклон обеспечивает измерение лямбды. Например, если предположить, что регрессия доходности акций компании Embraer в сопоставлении с доходностью бразильских суверенных облигаций ( -bond) дает наклон в 0,30, а так как средний наклон для бразильских акций равен 0,75, то лямбда будет равна 0,40 (0,30/0,75). [c.270]

Из равенства (12.41) следует, что применение обычного метода наименьших квадратов к наблюдениям yt приведет, в общем случае, к смещенным оценкам параметров /3. Если же а и = 0, т. е. когда механизм выбора и степень участия независимы, смещение отсутствует. Величину (p(z t i]I (z tl B (12.41) обозначают A(zj7) и называют лямбда Хекмана (He kman lambda). [c.344]

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, ~~только хардкор~~. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Термы:

переменная:	x
лямбда-абстракция (анонимная функция):	λx.t , где x — аргумент функции, t — её тело.
применение функции (аппликация):	f x , где f — функция, x — подставляемое в неё значение аргумента

Применение функции левоассоциативно. Т.е. s t u — это тоже самое, что (s t) u
Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е. λx. λy. x y x означает то же самое, что λx. (λy. ((x y) x))
Скобки явно указывают группировку действий.

Процесс вычисления

Рассмотрим следующий терм-применение:

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

который для простоты можно переписать как

(напомним, что id — это функция тождества вида λx.x )

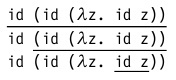
В этом терме содержится три редекса:

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y . Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y , а z — первоначальный терм имел бы вид (λx.λz.x)y и после редукции выглядел бы как λz.y . Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.

Так же бывает, что у нас есть абстракция λx.t x , причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t . Такое преобразование называется η-конверсией.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Читайте также: